基于实功法的结构刚度效率分析
2019-10-15罗若帆王仕成陈奇纳欧阳志勇
罗若帆,王仕成,陈奇纳,欧阳志勇
(1、嘉应学院土木工程学院 广东梅州514015;2、广东省建筑设计研究院 广州510010;3、悉地国际设计顾问(深圳)有限公司 深圳518048)
高层建筑结构方案的优化对结构设计至关重要,对于高层及超高层结构,刚度控制尤为重要,结构设计人员能否快速准确调整结构刚度,决定了结构设计全过程的效率。有学者运用能量法中的单位载荷法对控制点位移进行调整[1-2],但实际工程更侧重结构整体刚度的控制,实践表明该方法对结构刚度调整效率不高。文章通过简单算例,验证了SAP2000 软件虚功图的工作原理,并根据应变能和卡氏定理的关系[3],对比验证了软件的输出结果,推导展示了结构应变能与刚度的关系,以此为基础对结构刚度进行调整,并采用该方法对一超高层结构进行截面调整,结果表明该方法对快速准确调整结构刚度具有较高的效率。
1 实功法在桁架模型中的应用
1.1 桁架模型的建立
为验证实功法在软件中应用的可行性,在SAP2000 中建立简单二维桁架模型,设置所有杆件截面均采用φ100×6的钢管,材料均为Q345,不考虑结构自重,荷载工况仅考虑指定水平荷载,结构布置及荷载分布如图1 所示。
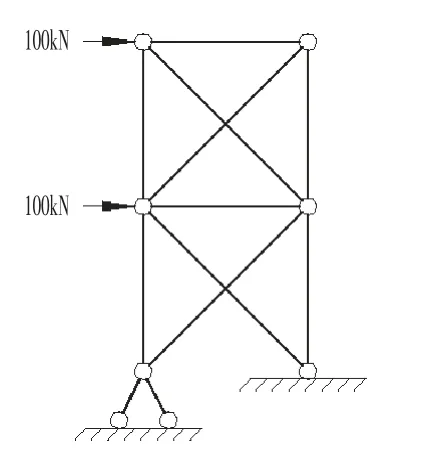
图1 结构布置Fig.1 Layout of the Structure
1.2 实功法的应用
基于“虚功原理”的虚功法仅考虑单位荷载作用位置为位移监测点,所有的调整均直接作用于该点。实际工程上更侧重结构整体刚度的控制,如满足层间位移角限值、结构顶点风振加速度限值等。因此采用另一种基于能量法的分析方法,即以外力功与结构所有构件应变能之和相等的实功法,该方法计算位移的能力不如虚功法灵活全面,但根据其计算原理,可高效运用于调整结构刚度。
已知外力所做的功,可表达为:

式中:Fi为作用点外力;△i为作用点位移。
应变能是结构变形过程中贮存在结构内部的势能,可分为构件应变能和结构应变能,结构应变能等于所有构件应变能之和,根据卡氏定理[4],杆件应变能计算公式如下:

桁架只考虑轴力,式⑵可简化为:
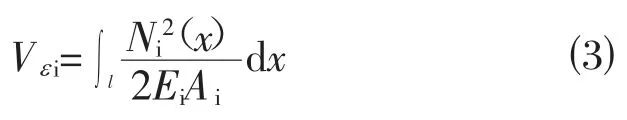
桁架中各杆截面面积和轴力沿杆长为常数,式⑶可简化为:

式中:vεi为杆件应变能;Ni为实际荷载下杆件内力。
根据能量守恒定律,杆件应变能等于外力功:

结构外力做功等于结构所有杆件应变能之和:

结构刚度与变形关系可定义为:
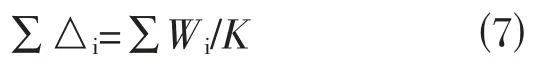
根据式⑴、式⑹和式⑺可得到结构刚度与应变能之间的关系:

由式⑻可知,结构刚度与杆件应变能之和成反比,由式⑶可知,应变能无负功,因此增大杆件截面,应变能总和将减小,结构刚度增加,而增大应变能较大的杆件截面,对该杆件的应变能减小较多,而内力重分布幅度较小,对其他杆件影响较小,因此对提高结构刚度有更好的效果。由于该方法在软件中的应用未见文献报道,故采用SAP2000 软件中输出虚功图的功能,通过该桁架算例,对该功能计算结果与手算进行完整的全过程对比。基于实功法,将实际状态和虚拟状态均设置为采用实际荷载分布,如图2 所示。
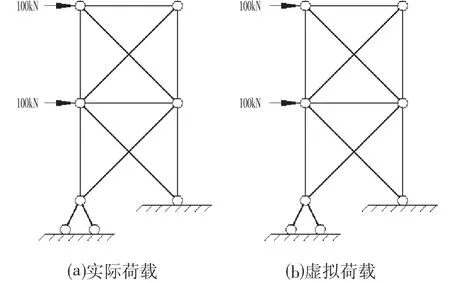
图2 荷载布置Fig.2 Load Distribution
由于SAP2000 输出虚功图数值为单位体积下的,即为:

杆件应变能除以体积V 为应变能密度,由式⑷除以V 可得:

为验证数据的准确性,对该桁架模型所有杆件进行手算应变能密度,并与软件数据进行对比,轴力图及软件输出虚功图如图3 所示,杆件按照输出虚功值的大小编号,由于10 号杆轴力为0,故不计算。计算对比结果如表1 所示。
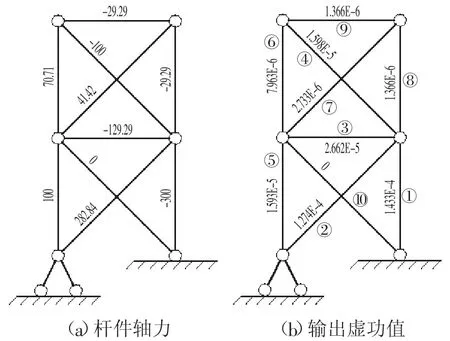
图3 杆件轴力及输出虚功值Fig.3 Axial Force of Members and Virtual Work Value

表1 公式计算值与软件输出值Tab.1 Formula Value and Software Value
从表1 数值对比结果可知,软件输出虚功图数值为应变能密度的2 倍,即无论实际工况与虚拟工况如何设置,其值均由式⑾计算:

该数值虽然与应变能密度存在2 倍的关系,但仍可反映应变能密度,根据式⑻,可知其与刚度之间的关系,显然通过增大应变能密度最大的杆件,对结构刚度的提高效率最高,为了更直观地观察杆件间的应变能大小关系,通过软件输出虚功相对值,如图4 所示。该数值为杆件虚功值除以虚功值最大的杆件的值,再乘以放大系数100 后的结果,按式⑿计算:

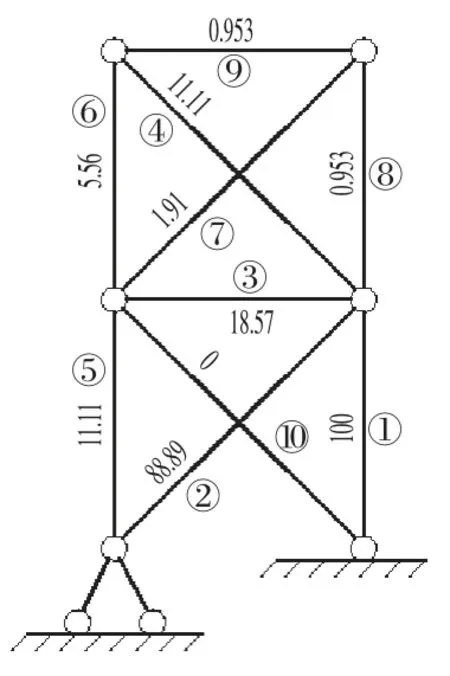
图4 应变能密度相对值Fig.4 Relative Value of Strain Energy Density
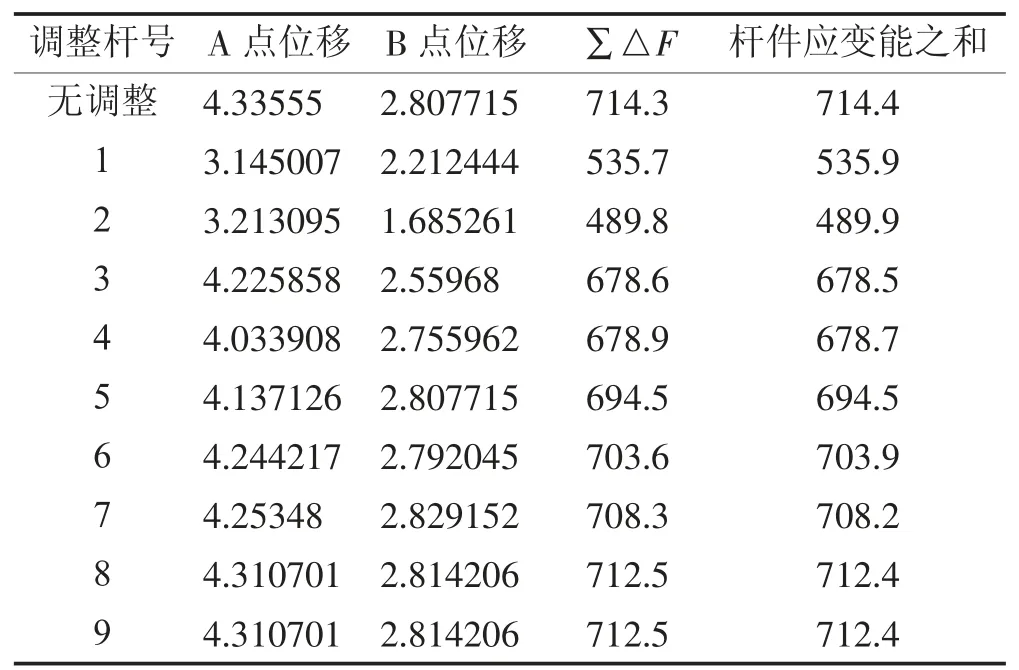
表2 调整各杆件截面的计算结果Tab.2 The Calculation Results after Adjusting the Cross Section of Each Member
根据调整结果可以看出,调整应变能密度大的杆件,减小杆件应变能密度和效率更高,由于外力做功等于杆件应变能之和,在外力恒定的情况下,总体位移将减小,杆件应变能之和减小的幅度大,则总体位移减小较多,而增大杆件应变能密度小的杆件,效率则较低。由于外力做功与应变能直接相关,由式⑽可知应变能密度与应变能的关系,由于2 号杆的长度比1 号杆长,因此虽然1 号杆应变能密度较大,但其应变能较2 号杆略小,实际工程中大部分构件均为竖直方向,长度相同,且尺寸不会相差太大,因此采用更直观的应变能密度相对值来调整杆件效率更高。
2 实功法在工程中的应用
在实际工程中,结构受力复杂,任何构件均承受轴力、弯矩、剪力、扭矩等作用,人工计算难度较大,因此可采用已在桁架模型中验证的方法,对工程模型进行调整。
2.1 工程概况
建筑为LOFT 公寓,结构体系为剪力墙结构,层数为35 层,层高为4.5 m,结构总高度157.5 m,抗震设防烈度为7 度(0.10 g),地震分组为第一组,场地类别为Ⅱ类,基本风压为0.55 kN/m2,地面粗糙度类别为C 类,体型系数为1.40。层间位移角限值为1/766(该工程执行《高层建筑混凝土结构技术规程(广东省标准):DBJ 15-92-2013》[5])。图5 为原结构布置图(结构布置完全对称,因此取原结构平面图的一半示意),最大层间位移角为1/643(27 层,Y 向风荷载工况),Y 向第1 周期为3.88 s。

图5 首层应变能密度相对值Fig.5 Relative Value of Strain Energy Density in the First Layer (kN,mm)
2.2 刚度调整
根据全楼应变能密度分布可以看出,全楼底部约1/4 高度范围内应变能密度较大,越往上应变能密度越小,因此可主要调整下部标准层截面,根据平面图应变能密度相对值(见图5),外围墙翼缘应变能密度值较大,内部剪力墙及梁数值较小,因此直接调整外围翼缘截面。由于需要控制刚度的方向为Y 方向,翼缘厚度为截面计算高度h,因此增大翼缘厚度对提高惯性矩I 更有效。截面调整情况如图6 所示(填充部分为增加的截面)。经过微小的调整,周期为3.49 s,最大层间位移角降低为1/767,满足规范限值的要求。
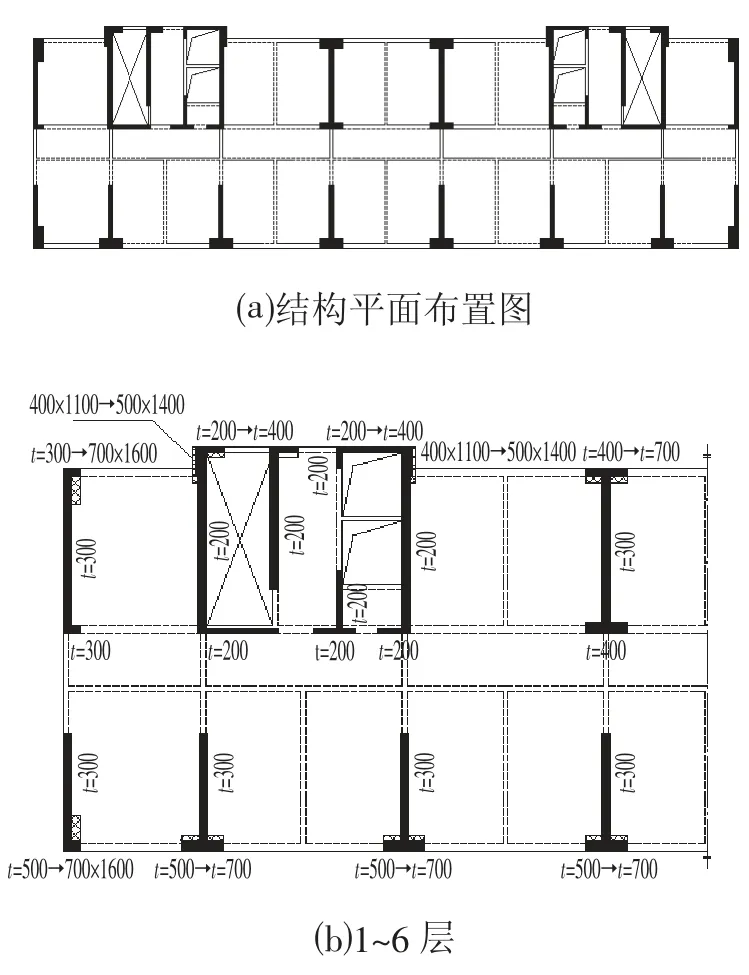

图6 结构平面图Fig.6 Structure Plan
3 结论
采用实功法可计算出结构应变能,并推导出应变能与刚度之间的关系,根据应变能密度的大小关系,可快速高效调整刚度。工程中结构构件应变能由弯矩、剪力和轴力等贡献,由简单桁架模型推导并验证的结论,可直接在工程结构中应用,根据应变能密度及大小关系调整截面尺寸,可高效地调整结构刚度。
