基于风带的海表面亮温增量统计模型*
2019-10-15李长军王颖芝
李长军, 王颖芝, 赵 红
(中国海洋大学数学科学学院,山东 青岛 266100)
在世界各大洋中,海表面盐度(Sea Surface Salinity, SSS)的变化是了解海洋在海洋生态系统和地球气候系统中扮演何种角色的一个关键参数。迄今为止,Argo剖面浮标实现了SSS领域最好的时空覆盖,提供分辨率约为3°×3°、每10天的SSS测量,然而,这个分辨率对于解决在SSS显著变化的重要时空尺度上仍然太粗糙[1]。
SMOS卫星于2009年11月2日发射,是世界上最早能够同时对土壤湿度和海水盐度变化进行观测的卫星,运转期间,将提供分辨率为200×200 km2的10~30 d平均的全球盐度数据,精度可达到0.1,但需要亮温的测量精度控制在0.02~0.07 K范围内[2]。在反演过程中,0.5K的亮温误差会导致1psu的盐度反演误差,且亮温误差和盐度反演误差成正相关,所以盐度反演精度对亮温精度有极为严格的要求[3]。L-波段海表面亮温的测量值依赖于SSS的同时,也依赖于海表面粗糙度、海表面温度、泡沫、入射角等其他因素,海表面粗糙度对亮温的测量影响尤为明显[4]。事实上,现实中的海洋是不平静的,海洋表面因为风的存在变成由波浪构成的粗糙表面,海表面亮温由两部分组成,一部分是平静海面辐射的亮温,另一部分是由海表面粗糙度导致的亮温增量[5-6]。在L-波段亮温反演SSS的过程中,海表误差的主要原因是风和泡沫诱导的海表面粗糙度对亮温的影响。
为了提高SSS的反演精度,特别是利用正演模型来减少海面粗糙度引起的误差,许多学者已经进行了大量的工作。在诸多亮温增量模型中,欧洲空间局选择3种正演模型对由海表面粗糙度导致的亮温增量进行计算:模型1是将海表面假想成很多小波浪叠加在大波浪之上,海表面粗糙度按照截止波长λ0分为大尺度和小尺度的双尺度模型[7];模型2是利用微扰法(SPA)和小斜率近似(SSA)展开发射率理论的直接发射率模型[8];模型3为半经验模型,SMOS卫星采取查表法(Look Up
Table)来描述作为若干个参数函数的亮温增量,该模型的输入参数分别是:入射角θ,风速WSn,风向φ_WS和有效波高SWH[9]。这三种模型实现SMOS卫星盐度反演得到的三种L2盐度产品数据分别记作SSS1,SSS2,SSS3,并且这3种盐度产品数据比较接近[10]。新版本V622的输出产品为SSS1,将SSS1作为SMOS L2盐度产品进行下面的分析与比较。通过本文构建的新亮温增量模型获得的海表盐度产品记作SSS4。
一般来说,海水盐度的变化较小,但会因海域所处的纬度位置不同有较大差异,主要受纬度、河流、洋流等因素的影响。SMOS卫星利用同一个亮温增量模型在低纬度海域和开阔海域反演的盐度产品精度较高,但在高纬度海域和近岸海域反演的盐度产品精度非常低[11]。考虑到SSS的时空分布与全球大洋环流密切相关,而洋流的形成与全球风带有着密切的联系。因此,本文根据纬度划分的风带,依据风对海面粗糙度影响,将全球海域按照风带划分成东南信风带(0°~30°S)、盛行西风带(30°S~60°S)、极地东风带(60°S~90°S)、东北信风带(0°~30°N)、盛行西风带(30°N~60°N)、极地东风带(60°N~90°N)6个海域,分别建立亮温增量模型,再计算各个海域的SSS。基于Argo实测盐度数据、SMOS卫星数据,我们可计算出受海表面粗糙度影响的亮温增量数据。在本文中,白冠覆盖率(Whitecap coverage)、有效波高(Significant wave height,以下简称SWH)、海表面温度(Sea surface temperature,以下简称SST)、降雨率(Rainfall rate)和蒸发量(Evaporation capacity)这5个变量的一阶、二阶、交叉项作为输入变量,然后利用LASSO统计方法筛选出与该海域亮温增量相关性较大的影响变量,在每个海域构建一个全新的二次曲线回归亮温增量模型。最后,将新模型嵌入SMOS卫星反演算法的程序计算中(L2OS软件),实现对软件的修正。该研究提高了粗糙海面条件下亮温数据的准确性,进一步提高了SSS的反演精度。
1 数据和方法
本次研究使用3个数据集,分别是Argo浮标数据集、SMOS数据集和辅助数据集。通过文献[12-14]了解到,海表面粗糙度受海表面温度、有效波高、白冠覆盖率、降雨率和蒸发量的影响。新模型将选取这5个参量作为海表面粗糙度的影响变量,相关数据由欧洲中期天气预报中心(ECMWF)提供。研究将集中在2015年5月的全球海洋,并在2015年6月进行验证(由于数据的限制,以一个月为例,其他时间的数据结果将在后续继续完成) 。
1.1 Argo实测数据
Argo(Array for Real-time Geostrophic Oceanography)数据由法国CORIOLIS数据中心(http://www.coriolis.eu.org)提供,作为本文的实测数据。Argo项目是一个实时的海洋观测项目,Argo浮标可以测量海水温度、盐度等海洋参数,具有自定位能力。取Argo测量的有效的第一层(-5 m)盐度数据作为海表面盐度的实际值,选择从2015年5月1日~2015年5月31日,在非极地水域均匀分布的13 783组数据进行建模,每个Argo数据组包括日、小时、纬度、经度和盐度。图1显示了每个可用的Argo点的位置。
图1 2015年5月份Argo测量点的位置
1.2 SMOS数据
SMOS卫星数据来自欧洲空间局(ESA),包括L1C亮温产品(数据版本为V620,https://smos-ds-02.eo.esa.int/oads/access/)、L2海水盐度产品(数据版本为V622)。SMOS卫星搭载的MIRAS仪器(Microwave Imaging Radiometer with Aperture Synthesis)能够探测地球表面L-波段(1.4GHz)的微波辐射,重建一个二维的、拥有多个入射角的亮温视野图像。L2海水盐度产品由L2OS软件生成,在SSS反演过程中,系统每2周进行一次OTT(Ocean Target Transformation)修正,旨在修正MIRAS实测亮温与模型模拟亮温之间总是存在的系统偏差,但季节偏差和纬度偏差依然存在[1]。
1.3 辅助数据
欧洲中期天气预报中心(The European Centre for Medium-Range Weather Forecasts,以下简称ECMWF,https://www.ecmwf.int/)集合了全球大部分的地面气象观测数据以及90%以上的环境卫星数据,可提供多种类型的数据用于地球地表及其周围大气环境的研究[15]。本文使用的ECMWF数据包括海表面温度、有效波高、白冠覆盖率、降雨率和蒸发量,数据版本为V318。
SMOS亮温数据与ECMWF辅助数据使用同一种等区域网格系统—ISEA 4-9。在1.2和1.3节中,利用2015年5月8日~2015年5月31日的所有上行和下行数据,建立亮温增量模型,并2015年6月1日~2015年6月30日的所有上行和下行数据验证模型。
1.4 数据匹配
由于Argo数据、SMOS卫星数据和辅助数据存在时空上的差异,因此在构建模型之前,需对南北半球的东南(北)信风带、盛行西风带、极地东风带6个海域的训练数据进行时间、空间上的匹配,包含以下几个步骤[16]:首先,将2015年5月的Argo数据按照经纬度信息与ISEA 4-9全球离散格网匹配,匹配遵循距离最近原则,最终获得12 111组全球有效数据。然后,将2015年5月的SMOS卫星数据、ECMWF数据按照网格点编号、最大时间间隔为1天与Argo数据进行时空匹配。考虑到不同入射角的问题,最后,得到南半球数据各为63 694、100 897和14 859组(H极化),63 621、100 834和14 853组(V极化);北半球数据各为80 693、76 887和5 916组(H极化),80 732、76 964和5 899组(V极化)。这些数据和由1.5节计算得到的亮温增量数据为本次研究的训练数据集,是构建6个海域亮温增量模型的数据基础。
1.5 亮温增量
海表面亮温可以分解为两部分:平静海面辐射的亮温和由海表面粗糙导致的亮温增量。海表面亮温在p极化(H水平极化,V垂直极化)时可以表示成以下形式[9]:
Tb,p(θ,SST,SSS,Prough)=Tb,p,flat(θ,SST,SSS)+ΔTb,p,rough(θ,SST,SSS,Prough) 。
(1)
式中:Tb,p,flat是平静海面辐射的亮温;ΔTb,p,rough是由海表面粗糙度导致的亮温增量;Prough为粗糙度参数;θ为入射角。
平静海面的亮温被定义为:
Tb,flat(θ)=e(θ)·SST。
(2)
e(θ)是L-波段的海表面发射率,携带了关于盐度的主要信息,与反射率Γ存在e=1-Γ的等式关系。在平静海面中,反射率可以通过菲涅尔反射定律直接计算,并提供一个精确的介电常数模型,对于每个极化方式下的反射系数R,均定义为海水介电常数ε和入射角θ的函数:
(3)
(4)
因此,平静海面的Tb,h,flat和Tb,v,flat可表示为:
Tb,h,flat(θ,SST,SSS)=(1-Rh(θ,ε))·SST,
(5)
Tb,v,flat(θ,SST,SSS)=(1-Rv(θ,ε))·SST。
(6)
海水的复介电常数ε依赖于温度和盐度,在微波段的任何频率都可依据Debye表达式计算[17]:
(7)
式中:i是虚数单位;ε∞是无线高频介电常数;εs是静态介电常数;ε0= 8.854×10-12[F/m]为真空下的介电常数;τ是豫驰时间;σ是离子电导率,ω=8.7965×109为电磁波的角频率。
基于1.4节匹配后的数据,可以计算出平静海面下,与Argo SSS和其他参数数据相关,各个入射角θ下的Tb,h,flat和Tb,v,flat,亮温增量可以表示为:
ΔTb,p,rough(θ,SST,SSS,Prough)=Tb,p(θ,SST,SSS,Prough)-Tb,p,flat(θ,SST,SSS) 。
(8)
Tb,p是由SMOS卫星通过反演迭代算法提供的亮温值,在这里认为是准确的。仪器校正后仍然存在的亮温偏差通过OTT进行校正,但是目前业务上OTT算法仍然受正演模型缺陷的影响,表现在当天顶角和入射角不同时,误差分布将有所不同,随着地表条件参数的改变偏差订正会有0.5K左右的变化[18]。
到目前为止,已经得到了所有的变量数据作为训练数据集,亮温增量是因变量(输出变量),而海表面温度、有效波高、白冠覆盖率、降雨率和蒸发量是自变量(输入变量)。然后,采用LASSO统计方法和二次曲线回归模型建立了亮温增量的统计模型。
1.6 LASSO统计方法
Tibshirani[19]在1996年提出了LASSO(The Least Absolute Shrinkage and Selection Operator)算法,通过该方法可以做到变量选择,即去除冗余变量,得到更重要的解释变量。它的具体表达式为:
(9)
通过选取非零系数的变量,得到一个可解释的模型。然后将所选的变量用于多元线性回归(MLR)中作为输入项,计算由海面粗糙度引起的亮温增量。所有匹配的数据点都将在训练模型中使用。
1.7 二次曲线回归模型
以二维自变量为例,假设因变量Y和自变量X1,X2之间有如下关系,称为二次曲线回归模型[20]:
(10)
其中,E(ε)=0且Var(ε)=σ2。
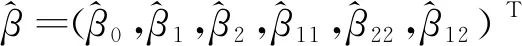
(11)
这里“经验”两字表示这个回归方程是基于前面的n次观测数据(x1i,x2i,yi),i=1,…,n获得的。
2 结果
在SMOS卫星的亮温观测中,同一个测量点会包括多个入射角θ对应的亮温结果,但其他辅助数据保持不变。本次研究仅对入射角为θ0的ΔTb,v,rough和ΔTb,h,rough建立统计模型,其他角度的亮温增量通过以下公式进行转换[21]:
(12)
式中:θ0为42.5°入射角;ρp(θ0)是不同极化方式下入射角为θ0的菲涅尔反射率。
2.1 模型建立
利用1.4和1.5节获得的训练数据集,选择白冠覆盖率、有效波高、海表面温度、降雨率和蒸发量的一阶、二阶和交叉项,共20个变量,作为待选变量。然后利用LASSO统计方法进行变量选择得到解释亮温增量的重要变量,再建立二次曲线亮温增量模型。最终筛选出各个海域在42.5°入射角,不同极化方式下5个相同的变量,分别是:SWH和SST的一阶、二阶和交叉项,表明这些变量在全球海洋中的重要作用。最后,使用选出的变量构造训练模型,并代入表1所示的估计回归系数。
ΔTb,p,rough(θ,SST,SSS,Prough)=A+B·XSWH+C·XSST+D·XSWH2+E·XSST2+F·XSWH·SST。
(13)
式中:XSWH2和XSST2是 SWH和SST的二阶项,XSWH·SST是SWH和SST的交叉项。
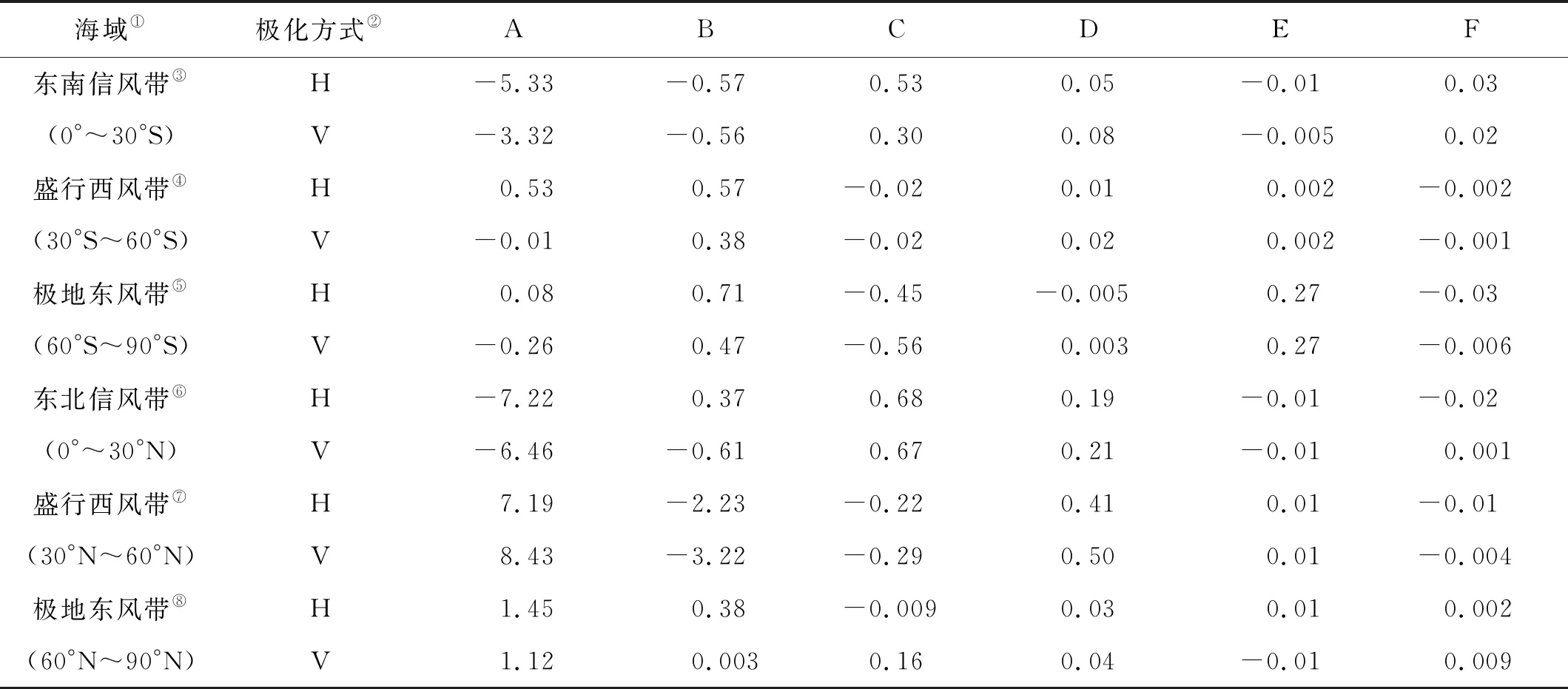
表 1 全球6个海域的亮温增量模型拟合系数
Note:①Area;②Polarization;③Southeast trade-wind zone;④Prevailing westerlies;⑤Polar easterlies;⑥Northeast trade-wind zone;⑦Prevailing westerlies;⑧Polar easterlies.
虽然在不同的海域通过LASSO选出了相同的影响变量,但这些变量的系数在不同的区域是不同的,表明每个变量对亮温增量的影响是区域相关的。因此,在全球海洋中使用同一模型来反演SSS是不合适的。
模型建成后,将新模型替换L2OS软件中现有的亮温增量模型,并将反演得到的SSS产品命名为“SMOS SSS4”。接下来,将在训练数据集和验证数据集上测试结果。
2.2 训练数据集误差分析
依据2015年5月的Argo浮标所在网格点,输出各个海域新模型反演盐度数据SSS4,原模型反演盐度数据SSS1与该时期、该区域的Argo浮标SSS数据进行匹配,匹配结果:东南信风带(0°~30°S)1242组,盛行西风带(30°S~60°S)2028组,极地东风带(60°S~90°S)284组,东北信风带(0°~30°N)1466组,盛行西风带(30°N~60°N)1280组,极地东风带(60°N~90°N)285组。经过计算,新模型在全球海域的绝对平均误差(MAE)和均方根误差(RMSE)分别是0.956 3和1.519 6,而SMOS SSS1产品的分别为1.711 7和2.528 8。各个海域的误差如表2所示,在全球海域和各个海域,新模型的盐度反演精度均优于原模型,同时绘制了SSS4和SSS1的误差百分比分布图(见图2,其中,model error对应SSS4误差,SMOS error对应SSS1误差)。

表2 训练数据集上的SSS4、SSS1与Argo实测SSS的误差对比
Note:①Area;②Error;③Southeast trade-wind zone;④Prevailing westerlies;⑤Polar easterlies;⑥Northeast trade-wind zone;⑦Prevailing westerlies;⑧Polar easterlies.
2.3 验证数据集误差分析
为了对模型进行验证,依据2015年6月Argo浮标所在网格点,全球共11 297个,输出新旧模型反演的盐度,与Argo SSS匹配,匹配结果:东南信风带(0°~30°S)1 741组,盛行西风带(30°S~60°S)2 438组,极地东风带(60°S~90°S)139组,东北信风带(0°~30°N)2 351组,盛行西风带(30°N~60°N)1 461组,极地东风带(60°N~90°N)204组。图3是SSS4和SSS1的误差分布图。图中30°N~60°N以及60°~90°(NS)中有偏离Argo数值较大的点,通过查看数据发现,30°N~60°N范围内陆地较多,偏离Argo数值较大的点大多分布在海陆交界处,受RFI影响较大,故反演误差大。而60°~90°(NS)为高纬度区域,Argo浮标少,用于建模的数据点少,导致模型自身的误差偏大,故反演误差大。经过计算,新模型和原模型在全球海域的MAE、RMSE分别为0.971 1和1.591 6,1.691 9和2.482 2,按风带划分的各个海域的盐度反演误差如表3所示,进一步说明新模型生成的盐度产品比SMOS L2盐度产品具有更高的精度,从实验的角度肯定了按风带划分全球海域反演盐度的正确性。
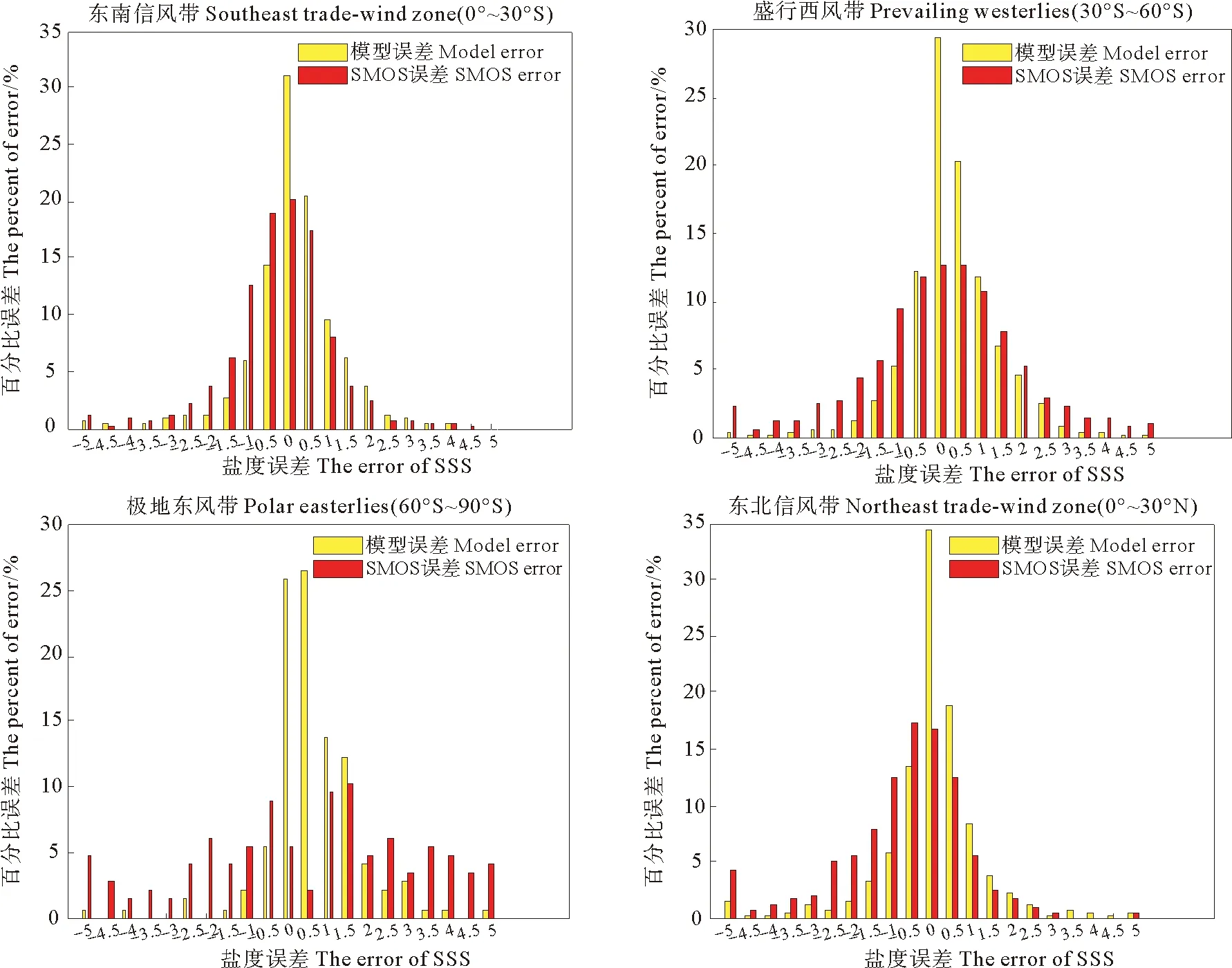
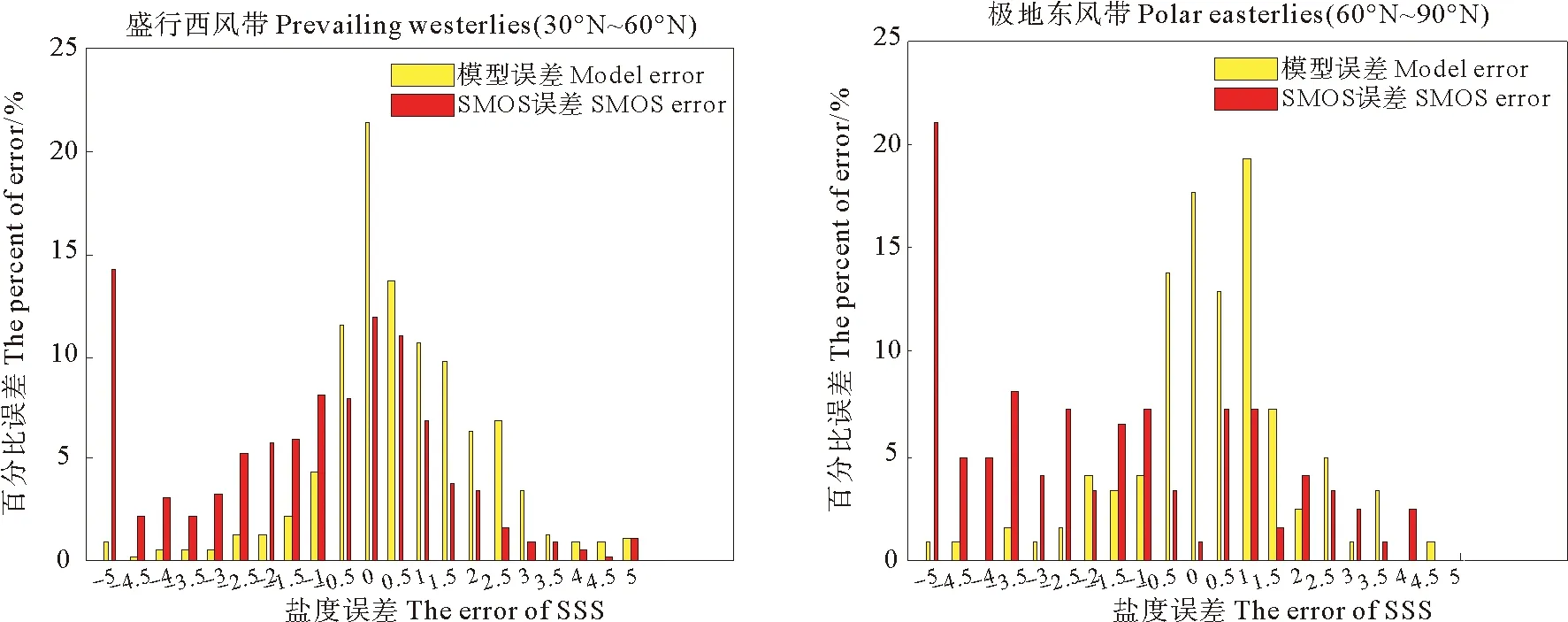
图2 训练数据集上的SSS4和 SSS1误差百分比直方图
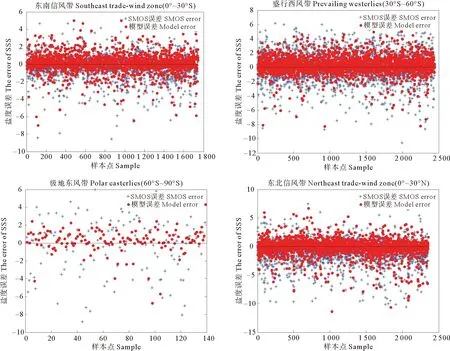
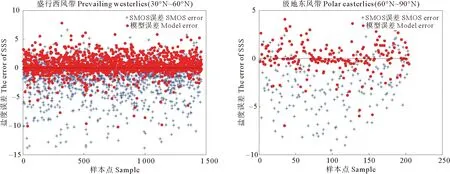
图3 验证数据集上的SSS1和 SSS4 误差分布图
Note:①Area;②Error;③Southeast trade-wind zone;④Prevailing westerlies;⑤Polar easterlies;⑥Northeast trade-wind zone;⑦Prevailing westerlies;⑧Polar easterlies.
取2015年6月1~10日的全球SSS数据进行平均,利用Surfer11软件绘制新模型的十日平均SSS图(见图4右),从ESA网站上下载SMOS卫星L3十日平均海水盐度产品数据,得到SMOS卫星L3十日平均SSS图(见图4左),同时绘制了SMOS L3 SSS与新模型SSS4的十日平均差值图(见图5)。可以看出2幅图的SSS变化趋势基本一致,图中新模型盐度值异于L3产品的海域大多靠近陆地,以及分布在高纬度海域,受RFI、数据点少模型误差大等因素的影响。地中海区域蒸发旺盛,周围河流淡水注入少,海水盐度高,新模型的反演精度高于原模型,所以新模型盐度值高于原模型是合理的。图中显示新模型的十日平均SSS图比SMOS卫星L3十日平均SSS图的盐度覆盖范围更为广阔,更加完整地描绘了全球盐度的分布情况,具有更高的实际应用价值。

图4 SMOS L3 SSS与新模型SSS4的十日 (2015年6月1~10日)平均图

图5 SMOS L3 SSS与新模型SSS4的十日平均差值图
3 结语
本文首次提出将全球海域按照风带划分成6个部分,利用LASSO统计方法挑选出包括SWH和SST一次项、二次项、交叉项在内的5个影响变量,在各个海域重新建立了有关亮温增量的二次曲线回归模型。在验证数据集上将新模型反演的SSS4产品与Argo实测SSS进行比较:南半球的东南信风带(0°~30°S)、盛行西风带(30°S~60°S)、极地东风带(60°S~90°S)以及北半球的东北信风带(0°~30°N)、盛行西风带(30°N~60°N)、极地东风带(60°N~90°N)6个海域新模型对亮温修正后反演的SSS4,MAE分别为0.76、 0.88、 0.93、 0.92、1.28和1.21。相对应的SMOS卫星L2日平均盐度产品数据(SSS1)的MAE分别为0.98、 1.61、 2.82、 1.50、 2.35和3.13。结果表明本次研究得到的亮温增量模型更适用于全球海域SSS研究,可以输出更高精度的SMOS卫星SSS产品。通过比较误差的直方图和分布图发现,新模型的盐度反演误差更加集中,且SSS变化趋势基本一致。
从整体上看,南半球海域的盐度反演精度高于北半球海域,因为北半球陆地覆盖多于南半球,受陆地射频(RFI)干扰大,因此模型误差较大。由于实验数据的不易获得以及完成一次实验耗费的时间长达1个月这两方面限制,模型的验证数据集仅停留在6月,与5月的训练数据集在时间上间隔较短,难以断定时间对模型预测的干扰程度,可继续利用7月、8月,甚至更大时间尺度的验证数据集评估模型,以获得模型预测的最大时间范围。同时,在实验中未考虑不同风带边界处是否存在不连续现象,也未对边界数据进行单独处理。在未来的研究中,可以通过考虑更多的影响因素,适当的结合相关的亮温物理机制,建立更为复杂的数学模型,更加准确地刻画亮温增量,得到更高精度的SSS产品。
