中空纤维径向压缩行为的有限元分析*

2019-10-14

产业用纺织品 2019年8期

中原工学院服装学院，河南郑州 450007

中空纤维是一种沿轴向具有管状空腔的异形截面(横截面)纤维，其结构特殊，故具有保暖、手感蓬松柔软及压缩回弹性和蓬松性良好等特点，广泛用于吸湿快干[1]、隔热保暖[2]和过滤分离[3]等领域，还用于制作冬季服装面料和床上用品，以及隔热填充材料和过滤膜材料的开发[4-5]。很明显，中空纤维的主要特征是其中空结构，这会直接影响纤维的应用价值。中空结构良好的中空纤维具备较强的静止空气锁定性能，这可为纤维集合体的保暖性能提供保障，但如果中空纤维的中空结构被破坏，其保暖优势就不复存在。一般情况下，导致中空纤维的中空结构不稳定的主要原因是纤维沿径向发生压缩。基于此，本文对中空纤维的径向压缩行为进行研究。

事实上，宏观中空管道材料的径向压缩行为已经引起很多研究者的兴趣。THOMAS等[6-8]通过试验对圆管在挤压过程中的变皱、弯曲和失稳3个阶段进行了分析。周亮[9]对线性强化圆管受刚性平面压缩进行分析，研究了圆环的横向压缩行为，探讨了接触面凹陷产生的机理，并提出了内凹产生的判据。张会杰等[10]采用TiNi相变圆柱壳进行径向压缩试验，利用数字摄像和图像处理技术得到了圆柱壳不同位置的变形特征和应变分布。邓大祥[11]采用不同软硬度的微沟槽圆管进行连续加载压扁试验，认为硬圆管在压扁过程中会依次产生一次塌陷、中间折痕、二次塌陷等严重的截面畸变，而软圆管的压扁变形比较均匀，截面畸变程度较小，能够在较小的压缩载荷下实现压扁成形。张坤等[12-13]先对钢质管道挤压变形过程进行数值模拟，然后对径向载荷作用下的管道进行挤压变形试验，得到了管道的挤压载荷-位移曲线和变形范围及管道压扁后的回弹情况和挤压过程中的塑性载荷等数据，验证了管道挤压过程中的安全性，并基于管道塑性变形理论和能量守恒原理，结合“Bow-tie”管道塑性变形计算模型，建立了径向载荷作用下的管道挤压变形模型，由此可对管道挤压过程中的塑性变形进行计算分析。班贵振等[14]对钢质管道进行挤压变形试验，得到了径向载荷作用下的管道塑性变形规律。艾池等[15]对侧向载荷作用下的套管塑性变形做了具体的计算和分析。由于纤维是一种细软的物体，测量单根纤维的压缩行为，其实际操作是很困难的。因此，本文运用有限元方法建立中空纤维径向压缩模型，再设定材料参数和边界条件，分析中空纤维的径向压缩行为，以期为稳定中空纤维的中空结构提供一些指导依据。

1 仿真试验

1.1 仿真模型

采用两向约束模式建立中空纤维径向压缩模型(图1)，对中空纤维的径向压缩行为进行仿真试验，同时假设：中空纤维截面及中空部分同轴且呈圆形，纤维纵向平行、伸直且无卷曲。从截面方向看中空纤维的径向压缩，相当于圆环的径向压缩。本文选择的仿真对象为涤纶中空纤维，其基本物性参数(即材料参数)：中空度为50%，直径为10.0 μm，密度为800 kg/m3，弹性模量为9 036 MPa，泊松比为0.26。

图1 中空纤维径向压缩模型示意

1.2 网格划分

采用有限元软件内置的网格划分方法进行网格划分，其中网格节点数为1 765，单元数为479。

1.3 边界条件

在中空纤维径向压缩模型(简称“模型”)的顶部(加载端)施加随时间线性增加的位移矢量，其步长选择100。模型的底部为固定支点(固定端)。

2 结果与分析

2.1 纤维截面形态变化

通过有限元软件模拟分析得出：在中空纤维的径向压缩过程中，首先是模型顶部(或底部)与加载端(或固定端)发生线接触，然后接触面积逐步扩大，形成面接触，线性增加的位移矢量所产生的位移载荷，其作用位置也随之移动，最终在中间部位产生凹陷。整个径向压缩过程大致可分5个阶段，纤维截面形态发生相应变化，如图2所示，其中(a)表示纤维径向未施加压缩载荷时的纤维截面形态，根据假设，此时纤维截面呈圆形。

(a) 圆形

(b) 椭圆形

(d) 过渡形态

(e) 花生形

(f) 8字形

(1)椭圆压缩阶段。在压缩载荷作用下，纤维截面沿加载方向的直径变短，使纤维截面从初始的圆形变成椭圆形，如图2(b)所示。分别与加载端和固定端接触的纤维截面顶部和底部被压平，接触部分由线接触变为面接触，纤维截面顶部和顶部产生直壁段，但其长度很短。

(2)跑道圆压缩阶段。随着压缩载荷作用的继续施加，直壁段逐渐增长，纤维截面变成跑道圆形态，如图2(c)所示。

(3)凹陷压缩阶段。当直壁段长度增长到一定程度后，由于纤维内外层受到的载荷不同，外层受压而内层受拉，压拉合力导致直壁段中间凹陷，形成图2(d) 所示的过渡形态；继而出现扁化现象，纤维截面发生畸变，此时的圆环由中间凹陷段、两侧扁化段和两边圆弧形段组成，纤维截面呈花生形，如图2(e)所示。

(4)凹陷深化阶段。随着压缩位移的增大，纤维受到的压拉合力不断增大，两边的圆弧形段具有同时向中间凹陷段积聚、两侧扁化段延展的趋势，凹陷和扁化程度逐渐加大，直到纤维顶部和底部凹陷至两个内表面接触，这时纤维截面呈8字形，如图2(f)所示。

(5)压溃深化阶段。纤维顶部和底部凹陷至两个内表面接触后，顶部凹陷段挤压底部凹陷段，推动下表面向两侧发生位移，可能产生轻微的二次凹陷。

2.2 纤维截面应力和应变

2.2.1 云图分析

图3(a)为纤维截面的形变云图，可以看出，最大形变发生在加载端和固定端附近(图中红色、蓝色部分)，形变分布呈现出一定的梯度并在圆周上扩散。图3(b)为纤维截面的应力云图，可以看出，最大应力发生在内圆的水平方向(即纤维截面的长轴方向)直径的两个端点(图中红色部分)及加载端和固定端附近，最小应力发生在左右两侧(图中蓝色部分)，应力分布呈轴对称，且呈现出一定的梯度。

(a) 形变云图

(b) 应力云图

中空纤维受径向压缩时，纤维内部的中空结构将垂直方向(即纤维截面的短轴方向，也就是载荷方向)的应力传递路径隔断，因此垂直方向的应力沿中空结构以外的部分传递，导致内圆的水平方向直径的两端产生应力集中。因此，中空纤维截面的水平方向和垂直方向的形变传递具有不同时性。

2.2.2 应变分布

在中空纤维的径向压缩过程中，纤维截面中性层的周长基本不变，纤维截面形变可以看成弯曲。图4 所示为中空纤维径向压缩前后的纤维截面微元，其中弧AB和弧CD表示纤维截面中性层，ρs和ρ′s、θc和θe分别表示径向压缩前后的纤维截面中性层的曲率半径和对应的圆心角。

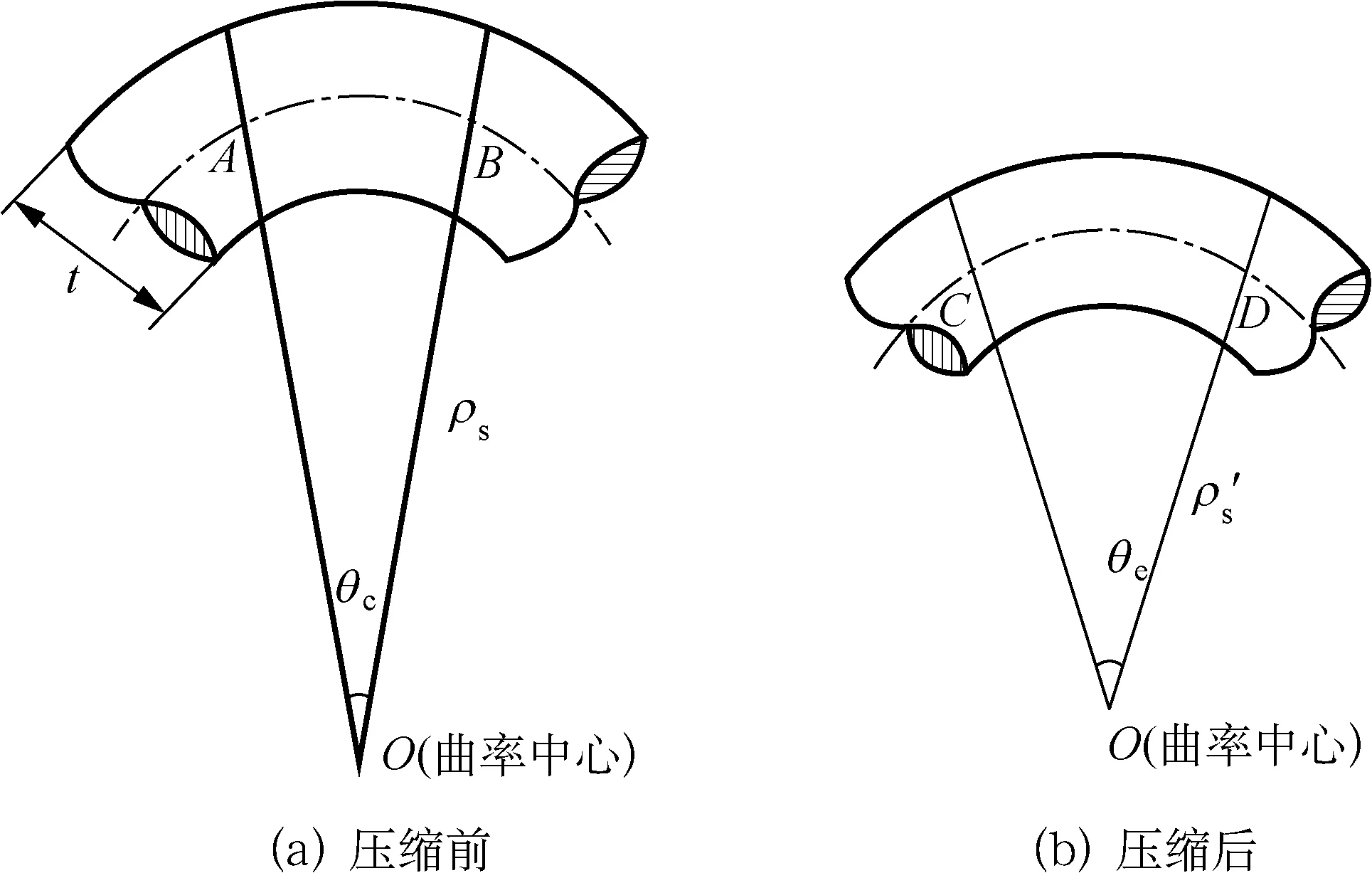
图4 中空纤维径向压缩前后的纤维截面微元段

按照文献[10]的方法推导，得到：

(1)

式中：εs——纤维截面外表面应变；

t——纤维壁厚度。

在椭圆压缩阶段，ρ′s可按下式计算：

(2)

式中：a、b分别表示纤维截面的长轴和短轴1/2的长度。

通过式(1)和式(2)，可以得到中空纤维径向压缩过程中纤维截面外表面不同位置的应变，如图5所示，显然其应变分布与形变云图相似。

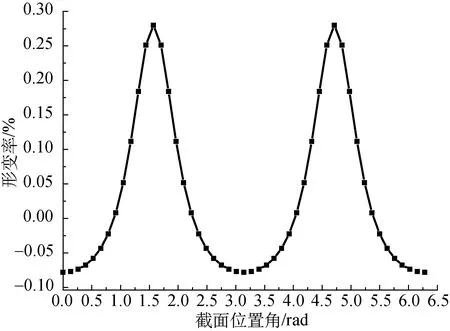
图5 中空纤维径向压缩过程中纤维截面外表面不同位置的应变

2.3 压缩载荷-压缩位移曲线

根据有限元模拟结果，绘制出中空纤维径向压缩过程中的压缩载荷-压缩位移曲线，如图6所示。

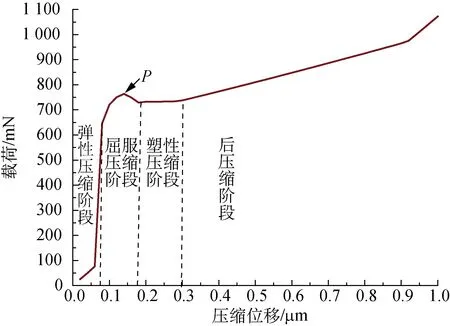
图6 压缩载荷-压缩位移曲线

从图6可以看出，压缩载荷-压缩位移曲线可以分为4个阶段：

(1)弹性压缩阶段。在压缩初期，即小形变区域，压缩载荷-压缩位移曲线形似直线，其斜率反映纤维的径向压缩弹性模量，表征纤维在低载荷条件下抵抗径向压缩形变的能力很强。在这一阶段，中空纤维的截面形态基本呈圆形，此时去除外力，纤维截面所发生的形变可以回复。

(2)屈服压缩阶段。随着压缩位移的增大，加载端和固定端与纤维接触面积逐渐变大，压缩载荷迅速增加，纤维截面两侧的圆弧半径不断减小，曲率不断增大，单位弧长上压缩载荷的垂直方向分力减小，压缩载荷-压缩位移曲线上出现屈服点P，纤维截面基本呈椭圆形或跑道圆形。

(3)塑性压缩阶段。进入压扁后期，纤维截面中间段出现弯折现象，所发生的形变能得到一定程度的回复，压缩变形抗力略微减小；随着纤维截面中间段的弯折不断加深，压缩载荷缓慢下降，压缩载荷- 压缩位移曲线的斜率逐渐减小，表明纤维的径向压缩弹性模量变小，压缩载荷-压缩位移曲线变得比较平坦。当纤维截面的上下表层的弯折相互接触时，由于纤维内表面沟槽相互支撑，压缩载荷增大，所发生的形变不易回复，纤维的中空结构被破坏。

(4)后压缩阶段。在压扁末期，纤维截面的上表层存在两个独立的压缩形变，所需的压缩载荷不断增大，纤维截面的下表层与固定端之间的接触区域逐渐扩大，即受力面积增大，因此压缩载荷-压缩位移曲线的斜率增大，直至纤维截面被破坏。

从图6还可以看出，中空纤维径向压缩过程中存在明显的屈服现象，屈服点P所对应的压缩载荷就是屈服载荷。在屈服点之前，中空纤维的径向压缩形变基本呈线弹性，此时去除外力，所发生的形变可回复；在屈服点之后，中空纤维的径向压缩形变能力明显提高，表明中空纤维承受径向压缩的能力明显下降。因此，要保持中空纤维的中空结构，屈服载荷是很重要的判据。在使用过程中，对中空纤维材料施加的压缩载荷应超过其屈服载荷。