基于多重节点的结构动力学显式异步长并行计算方法

马志强， 楼云锋， 李俊杰， 金先龙

(上海交通大学 机械与动力工程学院； 机械系统与振动国家重点实验室， 上海 200240)

大型复杂结构的有限元分析常涉及局部冲击载荷、接触等问题，需要针对特定分析部位划分精细化的网格[1].这类问题常采用显式算法求解，但受限于求解精度以及局部单元稳定性的要求，整个模型需要采用较小的时间步长，这会导致计算时间大大加长[2].因此国内外众多学者提出改进方案，期望可根据结构区域的特点，将结构分成不同属性的区域，针对单一区域选择合适的积分算法和时间步长进行动力学分析.

改进方法主要包括域分解法以及子循环方法两大类.域分解法是将计算区域分解为若干小的子区域，各个子区域单独计算.根据分区边界是否重叠可以将域分解法分为重叠与非重叠两种形式.重叠形式主要包括Schwarz迭代法和Arlequin方法[3]，非重叠形式包括Schur补方法和dual Schur方法，其区别在于处理区域边界约束的方式.张友良等[4]采用Schur补方法开发了岩土大规模并行计算软件.Farhat等[5]提出了以FETI (Finite Element Tearing and Interconnecting)为代表的dual Schur方法.刘铖等[6]基于FETI方法研究大变形柔性多体系统动力学方程高效求解算法.Kozubek等[7]将FETI方法推广到大规模非线性动力学并行仿真.

子循环算法是在一次计算步内包含两种时步即一次主步计算和多次子步计算的积分算法，主要用于解决分区步长不匹配的问题.早期研究者主要有Smolinski[8]与Belyschko[9]，研究对象多针对两分区的结构动力学问题.Prakash等[10]研究了非线性结构的异步长计算，通过拉格朗日乘子约束分区边界速度连续.刘占生等[11]将子循环与预测校正方法相结合求解壁板动力响应.高双武等[12]采用子循环的紧耦合算法，分析固体火箭发动机点火瞬态工作过程.

在上述研究中，域分解法可在一定程度上提高加速比，缩短计算时间，但不同计算区域采用相同的时间步长，在处理存在局部细分网格的动力学问题时，会造成计算资源的浪费.在经典的显式子循环方法中，分区多采用单元分割，不同步长边界节点信息传递过程常涉及插值或截断[13]，这在一定程度上造成计算不稳定、降低计算精度，也会限制最大步长比的选取[14].

为此，本文提出一种基于多重节点的显式异步长并行计算方法.该方法将多重节点引入异步长并行计算，显式小步长分区子循环过程中预测波形得以在显式重叠区域内完整传递，没有插值、截断误差，计算精度较高，不同网格区域可以采用较大的步长比.显式算法具有解耦特性(求解下一时刻的相关信息只需用到相邻节点上一时步的相关信息)，使并行计算过程不需要联立求解界面方程.因此，该方法具有一般显式并行算法易于编程实现的特点，同时相对于经典的子循环算法精度较高.

1 预测校正形式的显式Newmark求解格式

含阻尼的线弹性体结构动力学方程可以写为

(1)

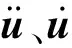
显式Newmark求解格式分为预测步与校正步.预测步中，第n+1时间步节点位移以及速度的预测值可以由第n时间步节点的位移、速度以及加速度表示[15]：

(2)

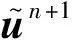
(3)

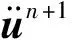
(4)

将求得的节点加速度值带入显式Newmark离散格式的校正步

(5)

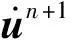
2 多重节点的显式异步长并行求解方法

2.1 异步长计算变量定义

结构有限元网格采用节点分割方法，将节点划分给不同分区，分割单元被相邻分区共享，并行计算过程需要共享分割单元信息.定义分区步长比：

(6)

式中：Δti为第i个分区选用的时间步长；Δtr为所有分区最小时间步长.异步长计算过程中涉及主时间步与子循环时间步，定义时间变量上标：

(7)

式中:X为某一变量；n为主时间步数；j为子循环时间步数.采用节点分割策略，定义节点布尔分割向量Oi，如果某节点在给定分区i，则该节点在分割向量中为1，否则为0.含多重节点的分区i布尔分割向量定义为：

(8)

则所有节点组成的分割向量O=INC.INC中所有分量都为1，NC为有限元节点自由度数目.

2.2 分区异步长显式并行求解

显式异步长求解过程需要重叠多层边界节点.图1是以2倍步长比的网格划分示意图.圆形表示内部节点，用I表示；三角形节点表示边界节点，用B表示；正方形节点表示外部节点，用E表示.阴影部分为共享单元.由节点重叠和分割单元相邻分区共享可知：分区边界节点是相邻分区的外部节点.

图1 异步长计算多重节点划分示意

参照分区节点分割向量的定义式，小步长分区分割向量为

Oi=

(9)

式中：OI代表内部节点分割向量(包含边界节点)；OE为外部节点分割向量.对步长比为mi的分区(为简化公式暂不包含阻尼)，离散的结构动力学方程可以写为

(10)

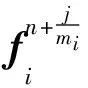
对于小步长分区的一个子循环时间步j，内部节点与边界节点的加速度可以写为

(11)

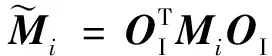
(12)

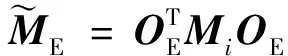
对于大步长分区，内部与边界节点的加速度求解公式与式(10)和(11)相似，不同的是此时分区时间步长为Δti=miΔtr，预测步与校正步中求解公式需要将时间步长换成miΔtr.大步长分区质量矩阵与刚度矩阵需按照分区分割向量分块.

3 数值算例分析

3.1 并行计算性能参数

算法的有效性在国家超级计算广州中心的“天河二号”超级计算机上进行测试，文中算例均采用CPU核心计算.并行算法的性能常用加速比与并行计算效率来进行衡量.异步长并行算法中，结构分区数以及步长比不同都会导致计算加速比不同.定义结构分区数目k固定，步长比m不同时加速比为

Ski=tkm/tki

(13)

定义m固定而k不同时加速比为

Smi=tmk/tmi

(14)

计算效率为衡量一个处理器的计算能力被有效利用的百分比，定义为

E=S/p

(15)

式中：S为加速比；p为使用计算核心数目.

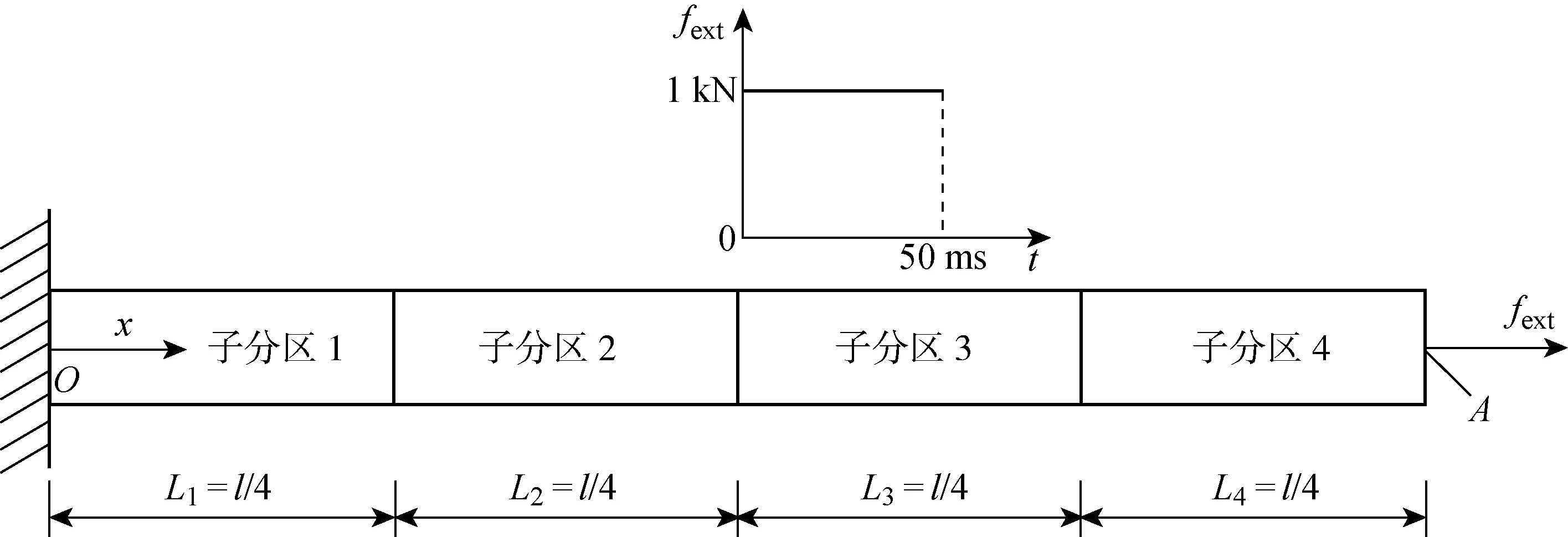
图2 弹性杆受轴向集中载荷

3.2 弹性杆承受集中轴向荷载

图2为弹性杆在轴向集中荷载作用下结构示意图.杆左端固定，右端点A受轴向集中载荷.杆材料密度ρ为 1 000 kg/m3，弹性模量1 GPa，横截面积 0.001 m2，杆的长度l为1 m，自由端加载外力fext为 1 000 N.x轴代表杆轴向坐标.整个结构划分为4个子分区，每个子分区长度为 0.25 m，每个子分区离散为200个两节点杆单元，整个结构有800个单元，801个节点.仿真时间 0.05 s.

子分区1、2、3采用相同时间步长，步长Δt为 2.5 μs.子分区4依次使用相同时间步长Δtr(Δt=Δtr)、5倍时间步长(Δt=5Δtr)与10倍时间步长(Δt=10Δtr)共3种情况.

图3为子分区4采用不同时间步长比，杆右端点A轴向位移(D)曲线与理论位移曲线.图4为图3的局部放大图.图3和4表明， 随着分区时间步长比的增加，位移的计算精度没有出现明显下降，依旧保持较高精度.

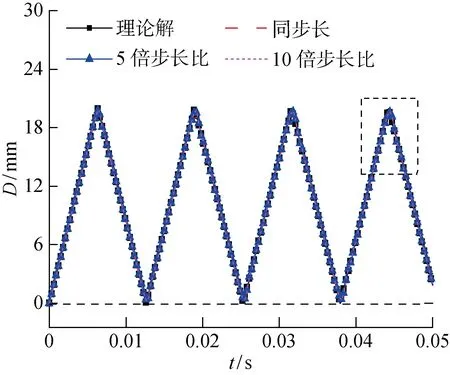
图3 右端点A轴向位移曲线

为比较网格特性对计算精度的影响，将子分区4进行细分离散，离散2倍，此时含有400个单元，而子分区1～3维持200个单元不变.子分区1～3仍采用步长Δt为 2.5 μs，子分区4采用步长比为10的异步长方法，计算杆右端点A的轴向位移.Belyschko方法是基于多重节点计算的经典方法，点A位移与Belyschko方法[9]进行比较.

采用2种方法计算得到的右端点位移曲线如图5所示，10倍步长比下位移曲线局部放大如图6所示.

(16)

式中：n表示主时间步数；Dthe为节点A理论位移；Dpro为采用给定方法计算的节点位移.统计的节点位移精度指标见表1所示.

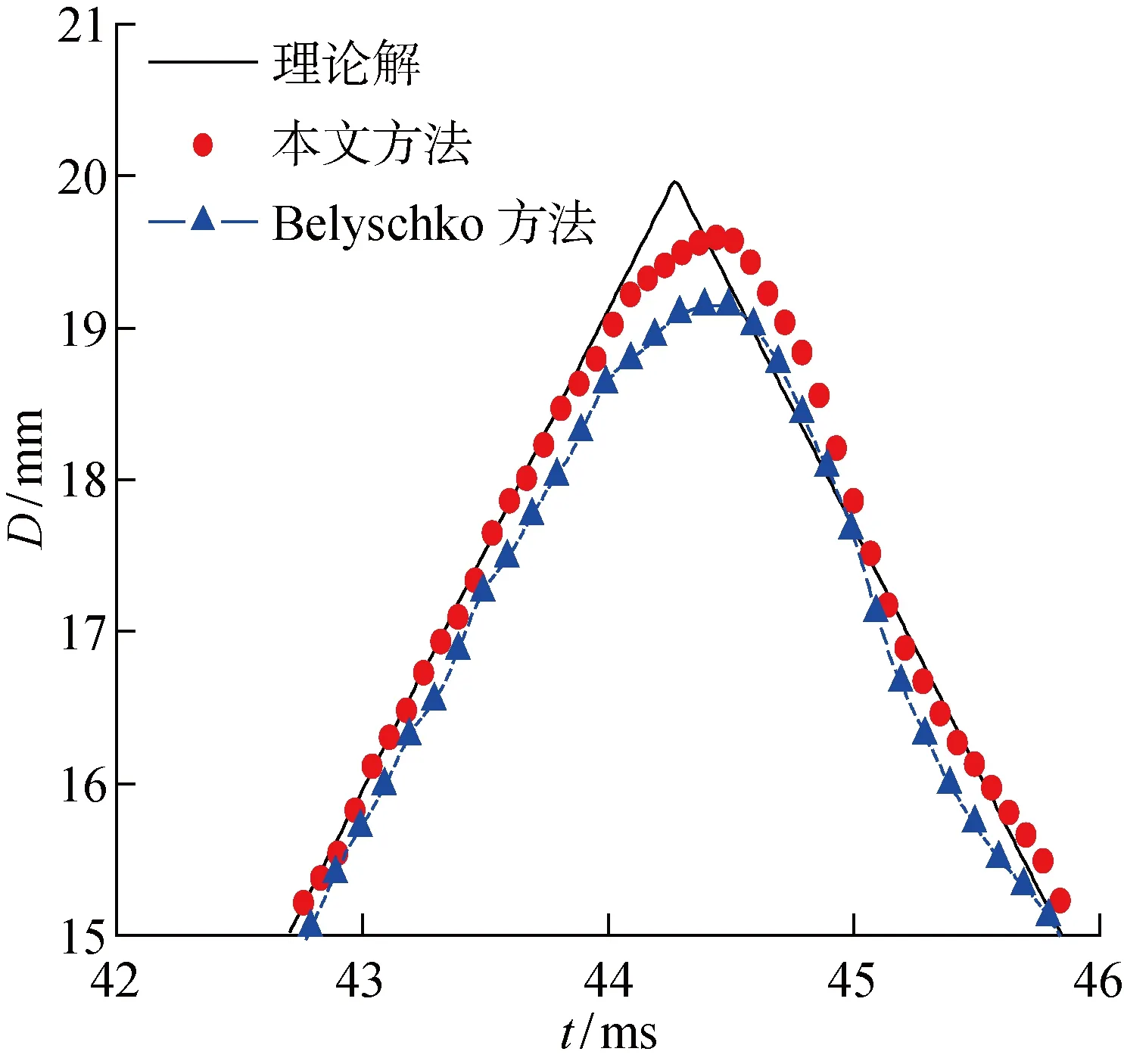
图6 图5的局部放大

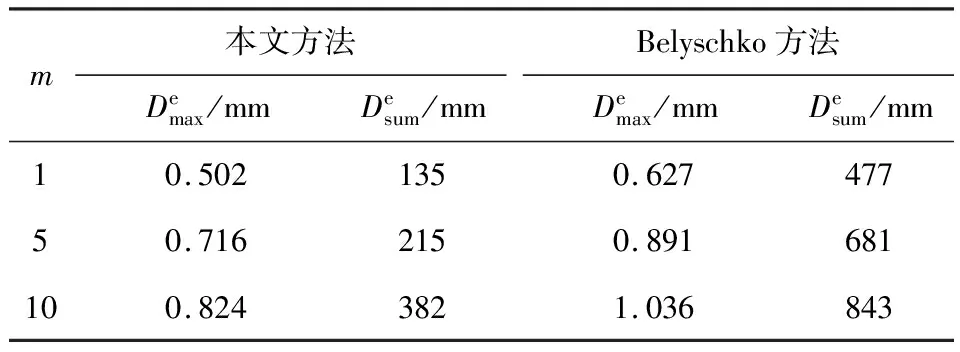
表1 节点A位移计算精度指标

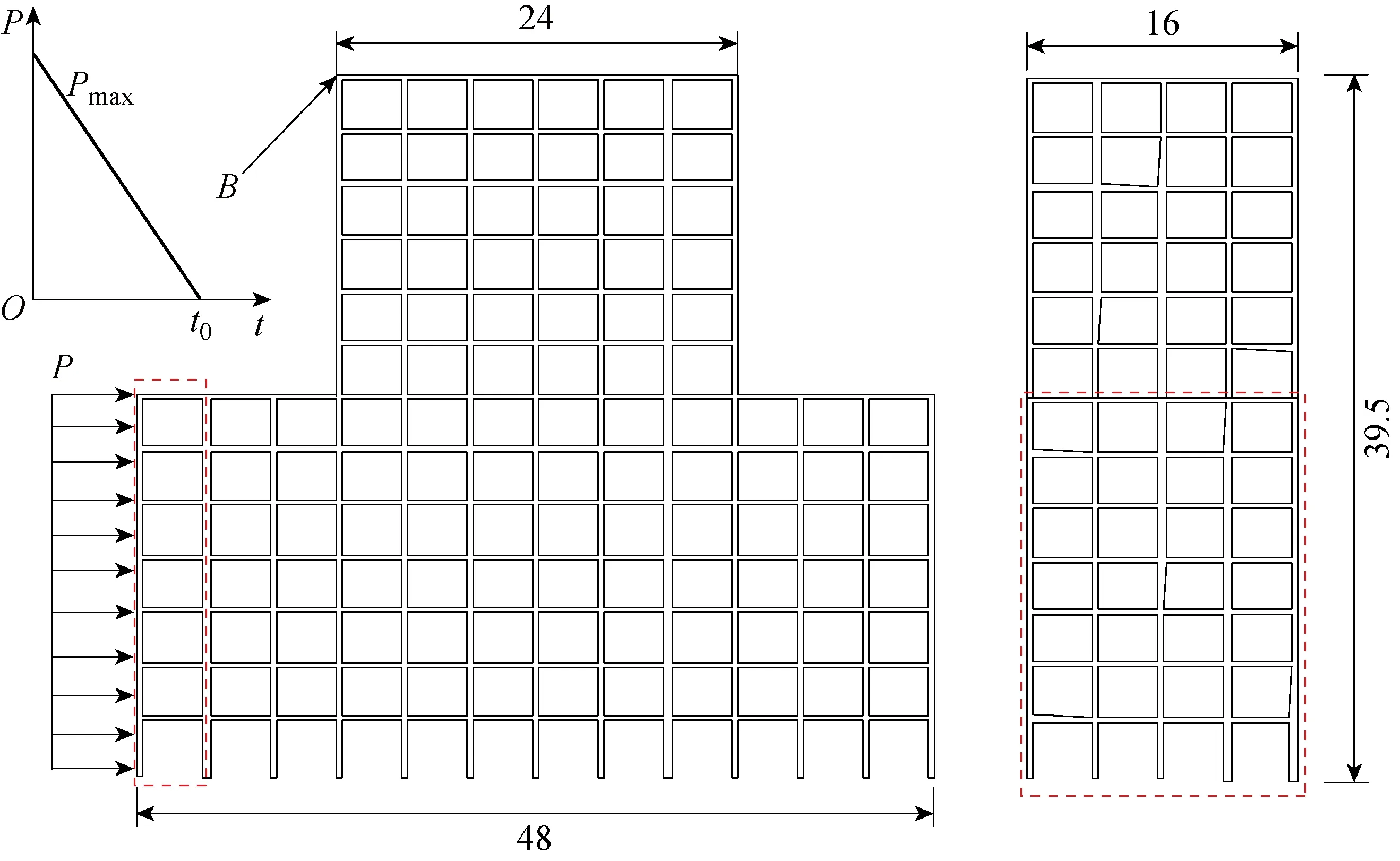
图7 多层建筑受冲击载荷(m)

从表1中可见：采用相同计算模型，随着步长比的增加，2种算法的最大计算误差以及误差和都在逐渐增加，计算精度相应降低.在相同步长比的条件下，与Belyschko方法相比，本文方法的最大误差以及误差和在数值上更小，计算指标变化的幅度也较小，表明本文方法具有较高的计算精度与稳定性.

3.3 多层建筑受冲击载荷

多层钢结构建筑模型如图7所示，整体建筑高 39.5 m，楼层底面长度为48 m，宽为16 m，建筑共有13层，其中最低层为高 3.5 m，其他楼层为3 m.整个建筑结构采用8节点六面体单元离散，离散后的该建筑模型含有 6 918 660 节点，5 212 768 单元，20 755 980 自由度.仿真工况计算采用对结构左侧面的右三角脉冲载荷.动力响应分析总时间为 0.6 s，大步长分区时间步长Δt=200 ms，总计 30 000 个主计算时间步.

为了验证本文并行算法的计算效率，建筑结构最右端(图7中虚线框区域)接受冲击载荷部位子分区采用较小的时间步长计算，计算建筑高层点B的位移曲线，P为冲击载荷，Pmax为三角冲击载荷的最大值.将整个建筑单元分别划分为120、240、480与960个子区域，小步长分区网格在120子分区时占据6个分区.

图8为建筑结构在步长比为4的情况下节点B的位移时间曲线，该实例计算结果与LS-DYNA软件计算结果较相符.建筑结构节点位移没有理论解，位移求解精度只做定性比较.

图8 多层建筑节点B的位移曲线

异步长并行算法中，分区数目与分区步长比都会影响并行计算效率.表2为各个分区采用相同的时间时根据显式异步长算法在不同计算核数下得到的并行效率.从表2中可知，随着计算核数的增加，计算总时间逐渐减少，计算加速比增加，但是从计算效率的角度来看，并行计算效率在逐渐下降.

表3为在图8中小步长分区m=4的条件下，随着分区数目变化的显式异步长算法并行效率.表3所得并行计算效率结论与表2类似，由两表格数据相比较可知：异步长并行条件计算下，步长比的选取对于并行效率没有实质性提升；但是，局部区域采用较小的时间步长，其他区域采用较大时间步长，计算总时间大幅度减少.

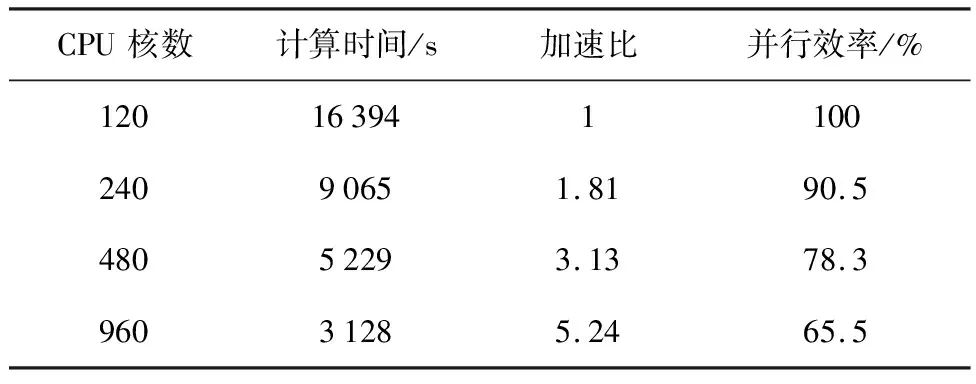
表2 分区同步长条件下计算效率(m=1)

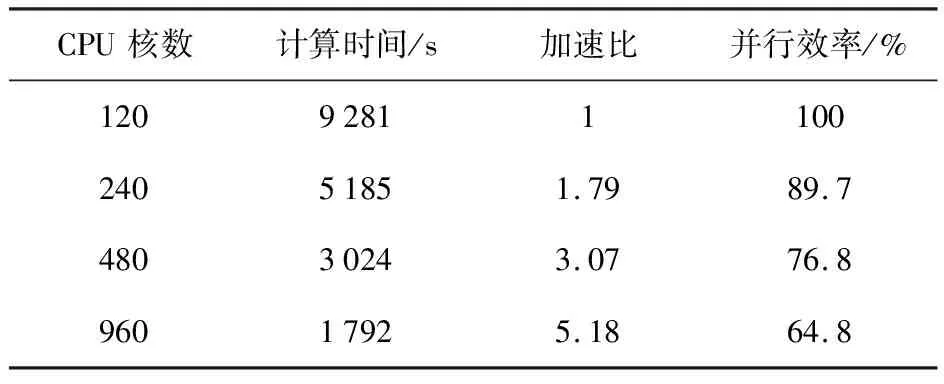
表3 同步长比条件下计算效率(m=4)

表4为在核数等于480时，随着最右端分区步长比变化所得的并行计算效率.由表4可以看出，随着步长比的增加，计算总时间与计算时间比率大幅下降，计算时间比率减少幅度在逐渐下降.步长比增加时，大步长分区计算时间降低有限，在一个异步长通信周期内，分区负载不均衡现象显现，因此研究负载均衡算法可以进一步提升显式异步算法性能，降低计算时间比率.

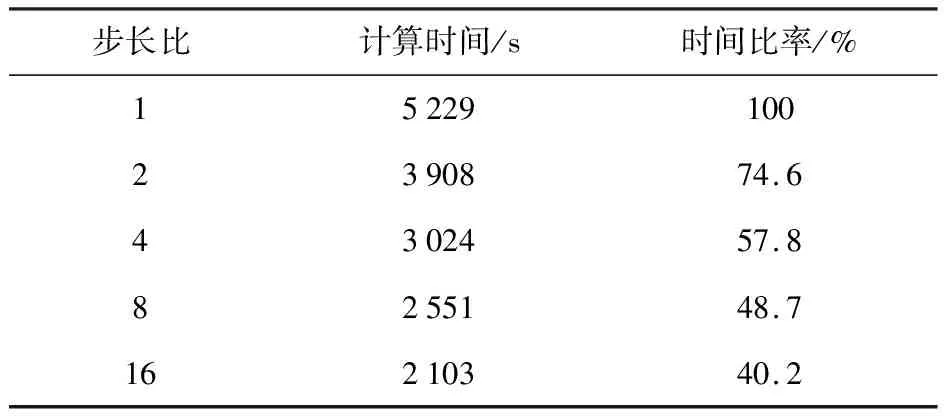
表4 相同分区数不同步长比下计算时间

4 结语

本文提出一种基于多重节点的预测校正形式显式异步结构动力学并行计算方法，该方法具有如下特点：

(1) 采用显式Newmark求解格式，对时间离散形式的结构动力学方程自由度解耦，边界信息传递只与相邻分区有关，提高了并行计算过程信息传递效率.

(2) 采用节点分割将计算模型分割成若个子区域，各个子区域选择各自的时间步长，解决了因局部精细网格造成的临界时间步长增加这一难题.

(3) 采用多重节点的分区耦合策略，相邻分区的部分区域设定为耦合分区，子循环过程中，预测波形得以完整地在整个耦合区域传播，而不是传统方法中经过截断的波形.这在一定程度上提高了计算精度.

研究结果也进一步表明，随着步长比增加，分区负载不平衡在一定程度上阻碍了计算效率的提升.因此，下一步研究的重点是提高异步并行负载的均衡性能.