求具有奇异的椭圆问题的一点函数值的高效数值方法

王桂娜，何文明

(温州大学数理与电子信息工程学院，浙江温州 325035)

对于一、二维的奇异椭圆问题的数值解法已经有不少人提出，文[1-5]研究了二维奇异椭圆边值问题的有限元方法，文[2-3]是将方程离散，用插值逼近的方法来讨论该问题．本文将针对一类常见的奇异椭圆问题，给出一种新的方法，来高效求解其在某一点的函数值，并给出了一个数值计算的例子．

1 方法和结果

对于椭圆问题

在本文，我们考虑，右端是奇异函数后，该如何高效数值求解u在某一点的函数值．我们的想法是：把u分解为u(x)=u1(x)+u2(x)，这里u1(x)是一个能精确找到的并且边界与u相同的函数，这样就能把对u的数值计算转化为对u2(x)的数值计算，其中u2(x)满足方程

假设Gx0是方程

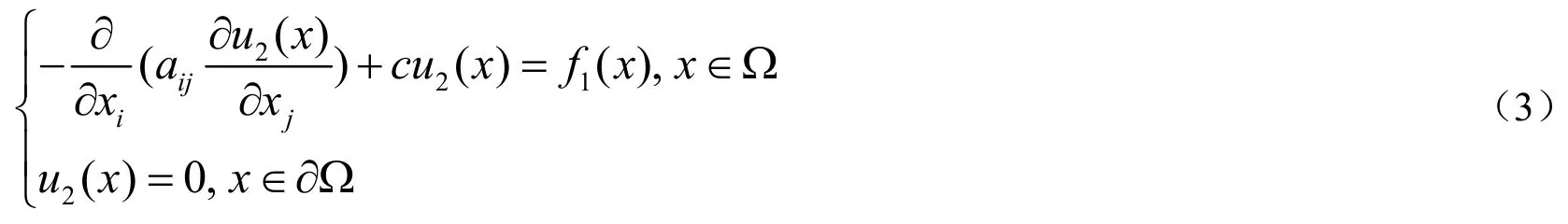
在点x0的格林函数，则可得到：

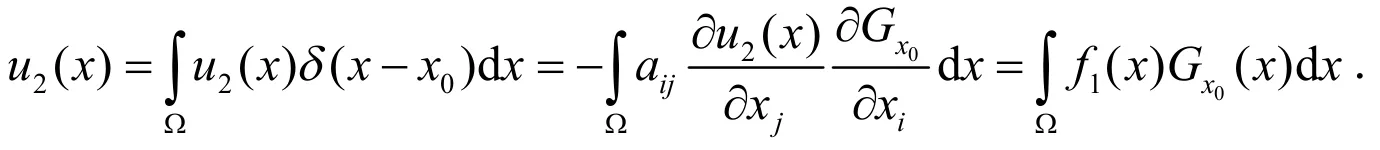
考虑到Gx0很难求精确解，把Gx0分解为：Gx0(x)=G1(x)+G2(x)，这里G1(x)满足方程[6]：

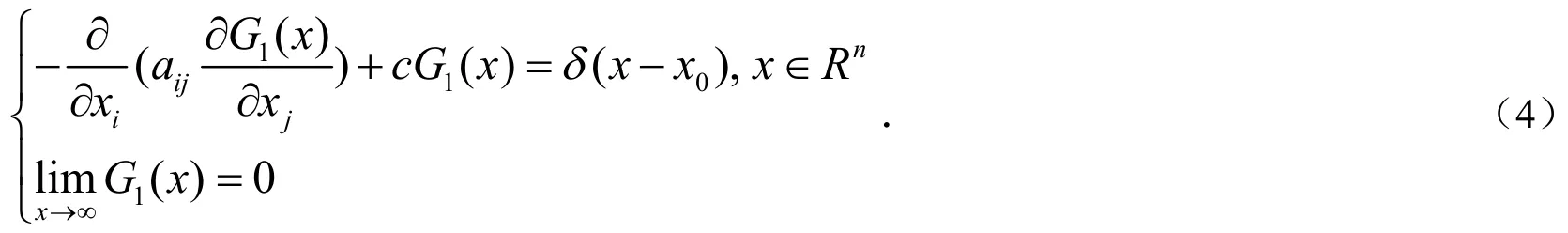
而G2(x)满足如下方程：

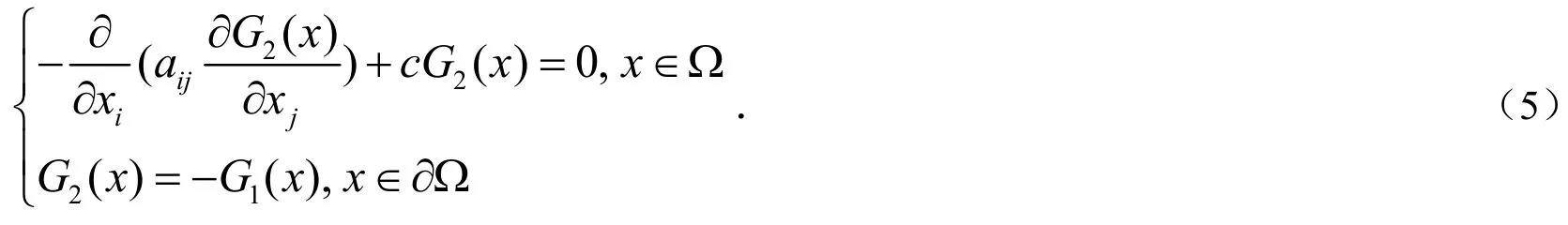
于是把u2(x)分解为：u2(x0)=u2,1(x0)+u2,2(x0)，这里

下面考虑如何计算G1与G2，先考虑如何具体计算G1(x)．

令对称正定矩形B满足：构造线性变换：y=B-1x．方程（4）可以变换为：

下面考虑如何求解方程（6）．当n=2时，令

并假设

由（7）式得到：

由（8）式得到：

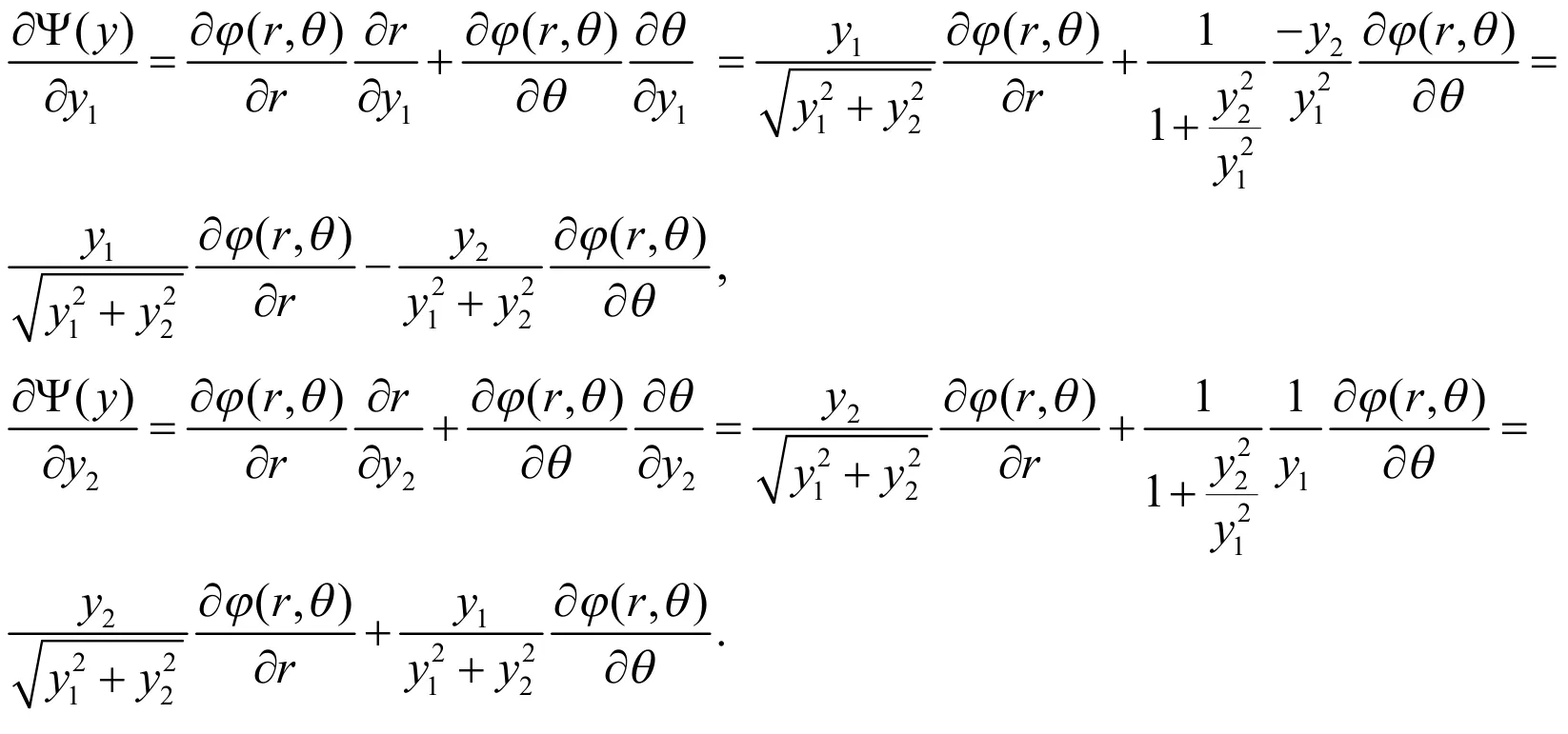
进一步得到：

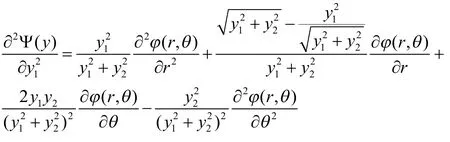
与

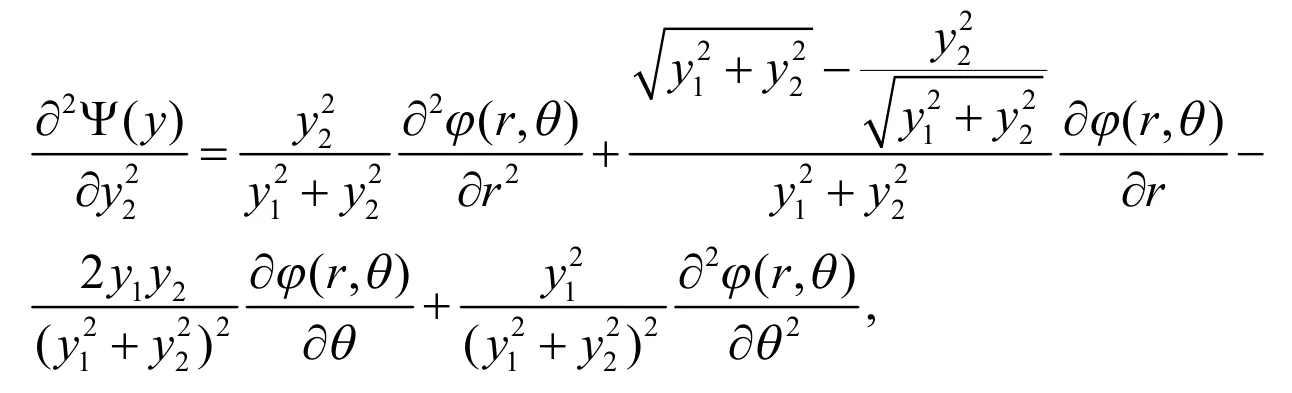
从而得到：

由分析可知，φ与θ无关，于是得到：

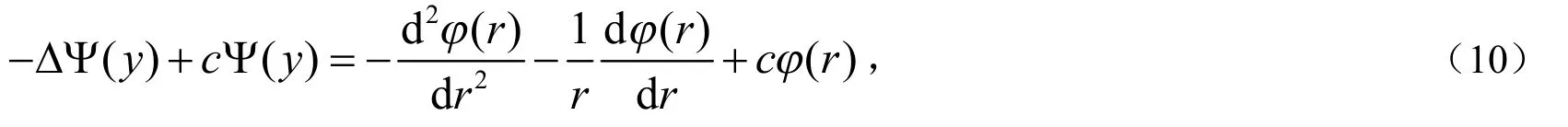
这样得到方程：

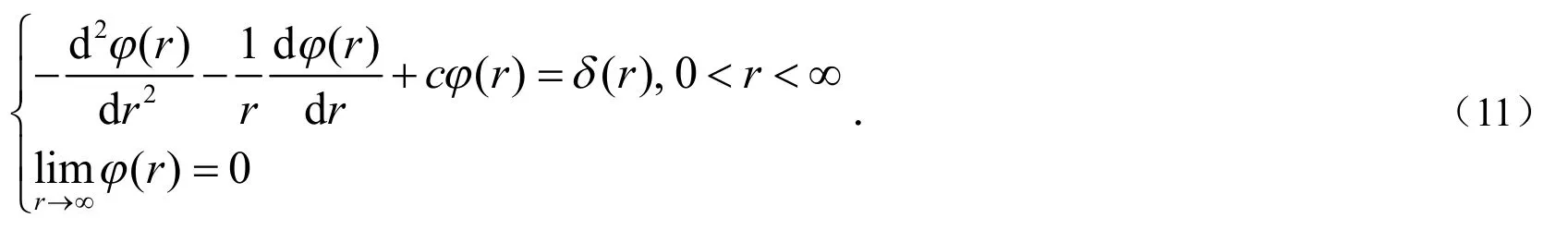
当c=0时，得到解析解[7]：当c≠0时，只能采用有限元方法得到近似解．同样的，当n=3时，能够得到方程：

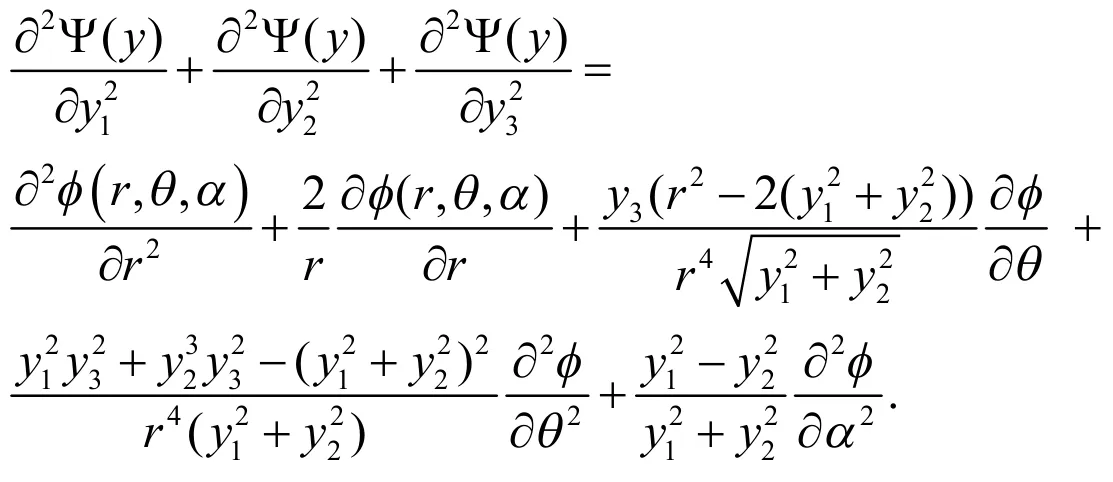
把该方程化为如下关于r的方程：这样可以得到：

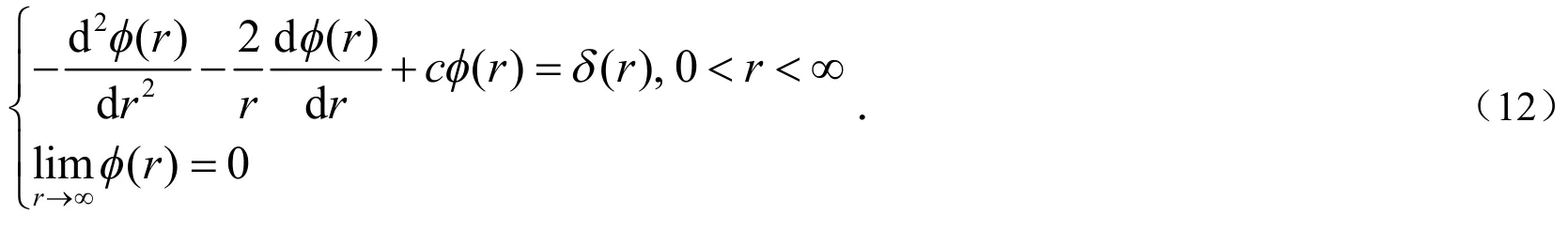
当c=0时，得到解析解：当c≠0时，采用有限元方法求解该方程，可以得到Ψ(y)的精确值，从而得到G1(x)．

对于G2(x)，可以用k次有限元方法来计算．由G1(x)与G2(x)，得到u2,1(x0)与u2,2(x0)．记现在我们来估计u2,2(x0)-Phu22(x0)．

定理1[8]存在不依赖于h的常数c，使得：

证明：

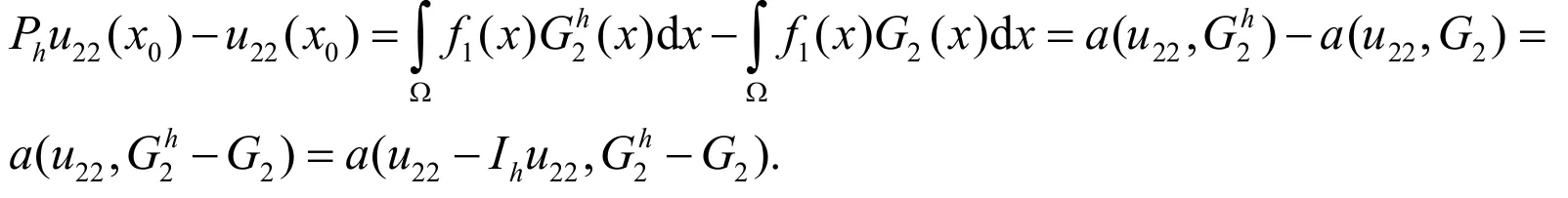
这里a(.,.)的定义为：从而得到：

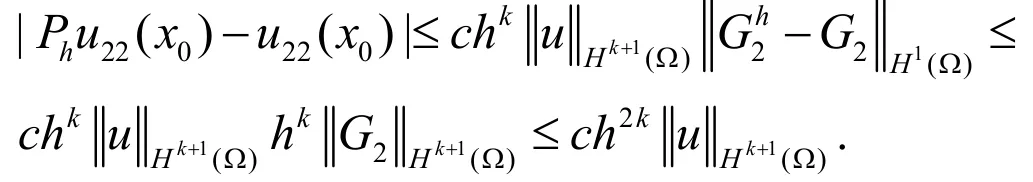
定理成立．

当方程（13）中c=0时，令：Phu2(x0)=u21(x0)+Phu2,2(x0)，则得到如下推论：

推论1 当方程（13）中c=0时，存在不依赖于h的常数c使得：

进一步，令Phu(x0)=Phu2(x0)+u1(x0)，则得到如下推论：

推论2 存在不依赖于h的常数c使得：

2 数值计算的例子

考虑方程：

我们要计算u在x=(1/100,1/100)点的值，构造δk次多项式函数φ1(t),t∈[-1,1]，使得这里1≤L2≤k．这里0≤L2≤k．

发现：

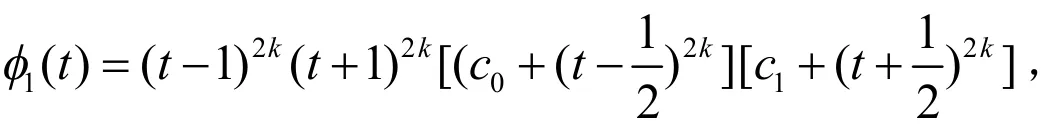
其中c0,c1满足解得

表1 给出方程（16）在点(1/100,1/100)处，本文得到的解与精确解之间的比较，其中hu是本文所得，u表示精确解，其中取k=1 ．

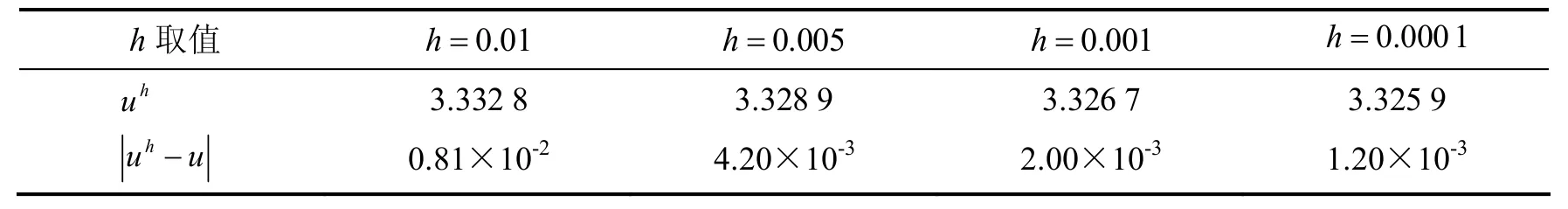
表1 u(1/100, 1/100)=3.324 7，本文解与精确解比较Table 1 Comparisons between the Solution from this Article and the Exact Solution,u(1/100, 1/100)=3.324 7

3 结 论

通常来说，奇异椭圆边值问题是不容易求解的，目前的文献中大多用差分法或有限元法求解，而本文通过格林函数法求解，因此本文具有一定的理论价值．