利用高分辨率水体反射地震资料研究吕宋海峡以东黑潮区混合*
2019-10-14张哲经志友唐群署
张哲, 经志友, 唐群署
利用高分辨率水体反射地震资料研究吕宋海峡以东黑潮区混合*
张哲1, 3, 经志友1, 唐群署2
1. 热带海洋环境国家重点实验室(中国科学院南海海洋研究所), 广东 广州 510301; 2. 中国科学院边缘海与大洋地质重点实验室(南海海洋研究所), 广东 广州 510301; 3. 中国科学院大学, 北京 100049
混合过程是海洋中普遍存在的一种形式, 对气候变化、物质分布等起到了重要作用。地震海洋学是近十多年发展起来的一门新兴学科, 被广泛应用到物理海洋学问题的研究中, 具有高空间分辨率的突出优点。文章利用反射地震资料, 通过斜率谱方法, 分别获得了吕宋海峡以东黑潮区湍流段与内波段的耗散率及扩散率。结果显示, 在剖面深度200~800m的平均耗散率为10–7.0W·kg–1, 平均扩散率为10–3.3m2·s–1, 比大洋统计均值10–5.0m2·s–1高约1~2个量级, 与前人在吕宋海峡的观测结果相一致。湍流段和内波段的扩散率空间分布差异较大: 湍流段扩散率高值区对应强流区域, 推测这里是中尺度涡边缘, 其次中尺度不稳定过程引起扰动增强, 进而引起湍流混合的加强; 内波段扩散率高值区出现在吕宋岛弧附近, 推测是内波遇到岛弧地形发生破碎, 进而引起强的内波混合。
黑潮区; 反射地震; 斜率谱; 混合
吕宋海峡是连接南海与西太平洋的唯一深水通道, 对南海与西太平洋之间的淡水输送、热量交换等起到了至关重要的作用。大量的观测研究表明, 在垂直结构上, 吕宋海峡呈“类三明治”的结构, 即上层水和底层水向西流向南海, 中层水向东流向西太平洋(Tian et al, 2006; Sheu et al, 2009)。
黑潮作为西北太平洋最强的暖流, 携带着暖而咸的海水由赤道向北输送, 对吕宋海峡的水文特征和环流状况有很大影响, 尤其是各种形式的入侵(Hu et al, 2000; Caruso et al, 2006; Nan et al, 2015), 加速了海洋的混合过程(Yang et al, 2014; Mao et al, 2016)。
混合过程是海水的一种普遍存在形式, 即海水的各种特性(如热量、浓度、动量等)逐渐趋于均匀的过程(冯士筰等, 1999)。海水混合有以下3种形式: 分子混合、湍流混合和对流混合, 其中湍流混合由海水微团随机运动造成, 交换强度比分子混合大许多量级, 是海洋混合的主要形式, 对流混合也通常表现为湍流混合状态(范植松, 2002)。因此, 湍流混合的研究是海洋混合研究中的关键问题。
海洋混合可以改变热量的分布和物质的输送, 影响海洋环流结构, 引起气候变化(Rahmstorf, 2003)。例如混合为大西洋南北方向上的经向翻转流提供了部分动力, 维持其运转所需的扩散率至少要达到10–4.0m2·s–1, 但实际大洋的观测结果仅为10–5.0m2·s–1, 这种“混合赤字”的现象在其他大洋中也存在。学者们希望通过小尺度的物理过程研究来弥补这一缺口。同时, 混合过程的研究对海洋参数化有重要作用。
众所周知, 海洋中存在不同尺度的运动, 能量由大尺度串级到小尺度, 经由湍流混合的形式耗散。所以对海洋混合的研究, 不仅可以解释海洋中能量的收支平衡问题, 还对海洋模式中耗散项的参数化有推动作用。除此之外, 海洋混合的研究对ENSO动力学、混合层动力学、海洋沉积动力学、河口海岸动力学、遥感海洋学、海洋声学及海洋生态学也有积极的推动作用(范植松, 2002)。在传统的海洋混合观测中, 海洋细微结构测量仪器如剪切流传感器、垂向微结构湍流剖面仪(vertical microstructure profiler, VMP)、湍流微结构剖面仪(turbulence ocean microstructure acquisition profiler, TurboMAP)、锚定式湍流观测仪(moored turbulence measuring instrument, MTMI)等发挥了重要的作用。其他研究发现, 采用斜率谱分析方法也可以定量计算得到海洋中的耗散率和扩散率(Klymak et al, 2007a, b)。
地震海洋学是一门新兴的交叉学科, 是用反射地震的方法来研究海洋水体的结构特征, 自Holbrook等(2003)的工作以来, 用地震海洋学方法来研究物理海洋学问题得到了广泛的应用, 包括海洋锋面、水团边界、地转流、内波、涡旋、温盐阶梯、混合等。与传统的物理海洋学观测相比, 地震海洋资料具有高横向分辨率、短时间内对海水剖面快速成像的特点(宋海斌等, 2008), 这些特点决定了它对物理海洋学中小尺度的研究具有极大优势。
本文利用反射地震的资料, 通过拾取反射同相轴信息用以代替水体波动, 计算得到水平斜率谱, 进而求出内波段和湍流段的耗散率和扩散率, 并对高值区产生原因做了推测分析。国内外在这方面也展开了广泛研究。Sheen等(2009)首次利用该方法计算了福克兰群岛东侧海域的一条地震剖面的海水耗散率和扩散率。Holbrook等(2013)利用反射地震资料计算了湍流耗散率, 给出了计算流程, 并详细讨论了影响耗散率计算的因素。拜阳等(2015)分别以南海内波和地中海涡旋为研究对象, 计算了其中的混合参数, 并在斜率谱拟合方法上采用效果更好的集合经验模态分解方法。Falder等(2016)指出存在一个从内波到湍流段的动力学转化机制, 但内波段与湍流段之间没有重叠区域。Sallares等(2016)通过对阿尔沃兰海的地震资料作谱分析, 发现内波段与湍流段之间存在K-H不稳定, 对能量串级和次中尺度过程有了进一步认识。
1 数据资料
本文收集并使用了位于吕宋海峡以东黑潮区的4种数据资料: 反射地震数据, 用来获取海水等密线的位移; 卫星遥感海表面高度异常 (sea level anomaly, SLA)数据, 用来得到航次测线周围的海流情况; Argo温、盐数据, 用来计算不同深度海水的浮力频率; 垂向混合坐标海洋模式 (hybrid coordinate ocean model, HYCOM)模式数据, 用来得到航次测线在不同深度上的流速。数据详细介绍如下。
1.1 反射地震数据
2001年8月4日至6日, 由国家973“中国边缘海形成演化及其重大资源的关键问题”项目委托广州海洋地质调查局, 利用“探宝号”调查船在南海东北部进行了地震数据采集工作。整个测线横穿中国大陆架、大陆坡、南海东北部、恒春海脊、吕宋岛弧、花东海盆和加瓜海脊, 如图1a中黑色线段所示。其中红色部分为本文研究所用的测线段, 总长180km。地震数据使用道间距为12.5m的240道水听器记录, 采样间隔为2ms, 记录长度为10s, 震源位于水深8m处, 容量为3000in3(约0.049m3)的枪阵, 炮间距为50m, 近炮检距为250m。

图1 2001年8月6日航次测线周围海域水深地形(a)和SLA(海表面高度异常)(b) 黑色线段表示完整的航次测线, 红色线段表示本文研究使用的部分测线, 箭头表示由SLA计算得到的地转流
地震数据的处理流程如下: 1)观测系统定义; 2)去除坏道; 3)去除直达波; 4)带通滤波处理(15~90Hz); 5)结合速度分析的叠前深度偏移; 6)偏移数据叠加; 7)谐波噪声压制(Tang et al, 2011; Holbrook et al, 2013)。最终得到了150~1500m深度范围的反射地震图像(图2a)。
进一步利用希尔伯特-黄(Hilbert-Huang)变换对图2a中的反射地震图像进行同相轴的自动追踪拾取(图2b)。由于观测系统最小偏移距的影响, 在反射地震剖面150m以上的表层看不到有效反射, 也拾取不到同相轴, 为保守起见, 在数据处理分析中剔除0~200m的上层同相轴。同时发现, 在左下侧吕宋岛弧地形处有错误拾取到的同相轴; 800m以下的同相轴由于噪声的干扰, 倾角过大且不符合物理规律, 同样属于错误拾取到的同相轴。将上述错误的同相轴剔除之后, 得到本文研究所用水体的同相轴, 深度范围200~800m, 水平跨度180km(图2c)。
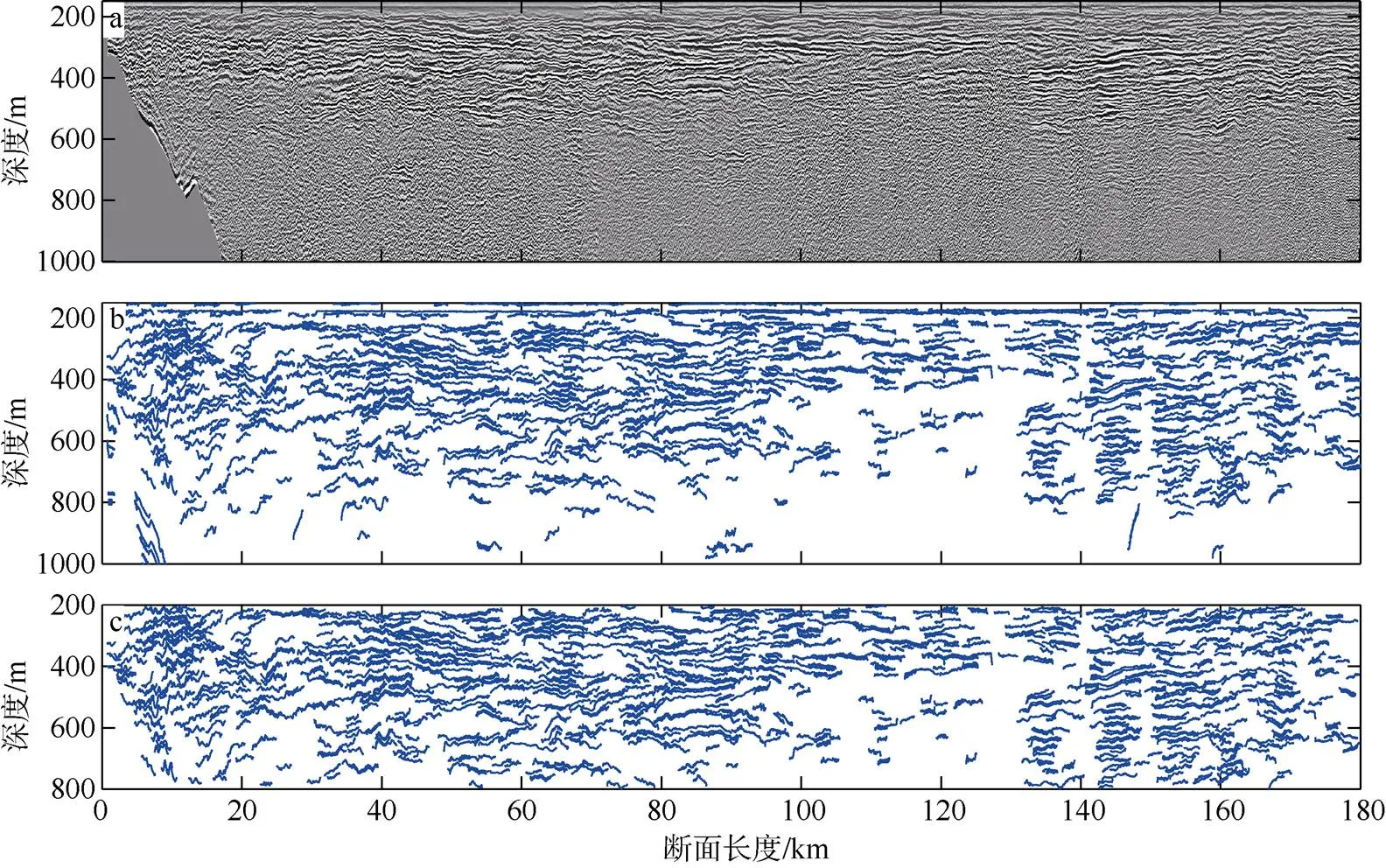
图2 水体反射地震剖面图像(a)、追踪拾取到的同相轴(b)、本文研究使用的同相轴(c) 对应图1中红色测线段
1.2 卫星遥感SLA数据
本文使用的卫星高度计资料由法国国家空间研究中心AVISO (Archiving Validation and Interpolation of Satellite Oceanography Data; http://marine. copernicus.eu/)提供。数据内容为网格化的海表面高度异常(SLA), 时间分辨率为日平均, 空间分辨率为0.25°×0.25°。文中选取的是2001年8月6日的数据, 与研究区域测线走航时间一致。按照地转理论中压强梯度力与科氏力相平衡(Stewart, 2008), 可以将上述SLA数据计算得到地转流, 计算公式为:

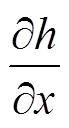
1.3 Argo温、盐数据
本文用来计算浮力频率所使用的温、盐数据来自中国Argo 实时资料中心(http://www.argo.org.cn/), 选择的数据产品为《Argo网格化温盐产品(G-Argo)》, 时间范围为2000—2008年, 时间分辨率为每周一次, 空间范围为120°E—90°W、90°S—60°N, 空间分辨率为3°×3°, 垂向0~2000m共36层。
本文选择测线周围4个节点: (121°30′E, 19°30′N)、(124°30′E, 19°30′N)、(121°30′E, 22°30′N)、(124°30′E, 22°30′N), 通过这4个节点将2000年1月5日至2008年12月31日共计470周的数据计算得到浮力频率值, 先后作时间平均和4个节点的平均, 将结果作为测线不同深度的浮力频率值(图3), 用于后面水平斜率谱的校正。

图3 浮力频率随深度的变化曲线 竖直红线表示参考浮力频率值(3.0cph), 竖直绿线表示研究区域浮力频率均值(3.9cph), cph为周频率cycles per hour的缩写,1cph=(1/3600)s
1.4 HYCOM模式数据
本文使用的模式由HYCOM提供, 下载网址为https://hycom.org/, 选择下载再分析的流场数据, 数据全称为Global Ocean Forecasting System (GOFS) 3.1 output on the GLBv0.08 grid, 时间范围为1994年1月1日至2015年12月31日, 时间分辨率为3h; 在空间上: 40°S—40°N间的空间分辨率为0.08°, 其余区域为0.04°。最后选取与走航测线同期的流场数据。
2 计算方法
2.1 内波段与湍流段区间划分
本文选取数据中水平长度大于1.25km的同相轴, 共计916条, 将每一条同相轴做距平处理(即减去其所在深度的平均值), 得到同相轴的垂直位移。由于同相轴位移近似于等密线位移(Holbrook et al, 2013), 因此用同相轴位移代替等密线位移来作斜率谱分析。
采用Welch方法并选取128个点的傅里叶变换长度和半重叠的Hanning窗, 对上述每一条同相轴位移计算其功率谱密度, 得到水平波数谱。每条水平波数谱均乘以(2π)2(其中为波数), 得到水平斜率谱。这样做能够更好地把内波段和湍流段区分开来, 因为在双对数坐标下, 斜率谱内波段斜率为–1/2 (Garrett et al, 1975), 湍流段斜率为1/3 (Batchelor, 1959), 正负值交替更容易区分。除此之外, 由于内波的垂向位移依赖于局地的海水层结, 因此斜率谱需要通过浮力频率校正来消除层结的影响(Sheen et al, 2009), 即在水平斜率谱上乘以(/0), 其中为该同相轴所在深度的浮力频率,0=3cph为参考浮力频率。以下分析均使用校正后的水平斜率谱。
上述916条水平斜率谱的平均如图4所示, 左侧内波段(斜率为-1/2)和右侧湍流段(斜率为1/3)分界明显。由于内波段和湍流段之间转换部分的动力过程同时受内波和湍流影响(Sheen et al, 2009; Falder et al, 2016), 斜率谱最低波数段受带宽的限制, 最高波数段受噪声的影响, 因此本文剔除上述区间, 从而划定内波段范围为: 0.0013~0.0044cpm (cpm为周波数cycles per meter的缩写), 湍流段范围为: 0.0088~0.03cpm(图4), 并应用于所有水平斜率谱(图5)。
2.2 混合参数估算
完整的斜率谱模型包括3部分的运动形式: 内波、惯性对流和惯性扩散(Klymak et al, 2007a, b):
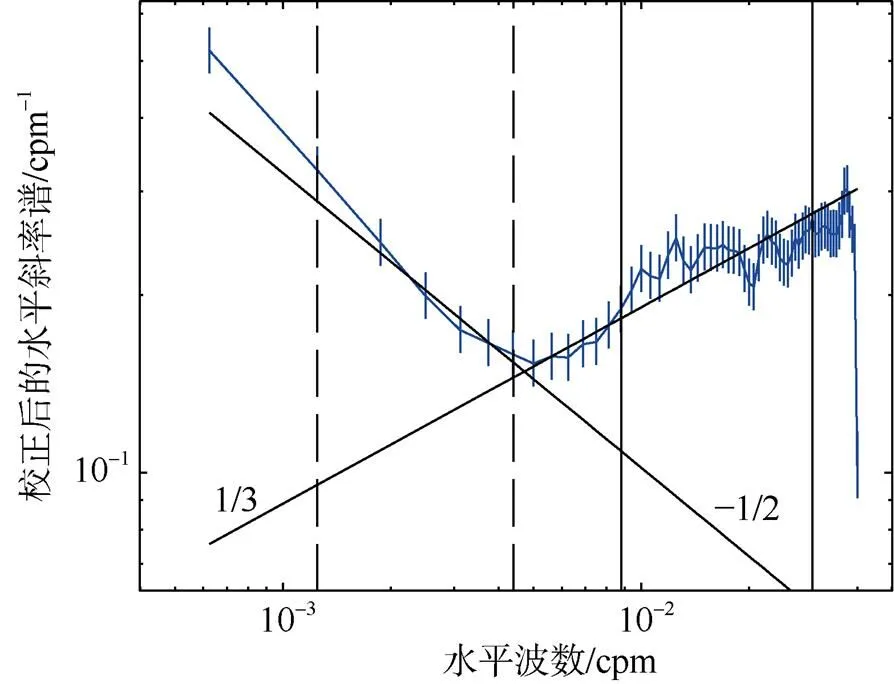
图4 水平斜率谱的平均 共使用916条水平斜率谱计算谱的平均, 误差棒表示95%置信区间; 竖直虚线内为内波段区间, 竖直实线内为湍流段区间; 两条倾斜线段斜率为1/3和-1/2, 分别用来拟合湍流段和内波段的斜率谱
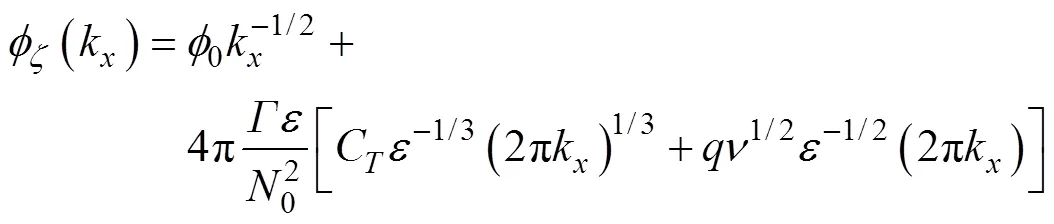
在高波数的湍流段, 波数谱的斜率与类Kolmogorov律(–5/3)相一致, 采用Batchelor模型(Batchelor, 1959)拟合, 即湍流惯性对流子区:

其中, 是湍流段波数谱; Γ是混合效率, 根据经验取值为0.2; N是斜率谱所在深度的浮力频率; 是常数, 约为0.4(Sreenivasan, 1996); 是湍流耗散率; k是水平波数。
在低波数的内波段, 功率谱与内波GM75模型(Garrett et al, 1975)相一致, 波数谱斜率为-2.5, 采用Gregg-Henyey参数化模型拟合。有充足证据表明, 在开阔大洋中, 耗散率与内波能量的二次方成正比, 根据内波的波-波相互作用理论,等于其在高波数段通过内波谱的净能通量, 据此得到与观测结果符合最好的平均湍动能耗散率计算公式(Henyey et al, 1986, Gregg, 1989):

在斜率谱中, 湍流段给定斜率为1/3, 其耗散率根据最小二乘法原理和公式(3)拟合得到; 内波段耗散率由公式(4)的参数化方法计算得到(图5)。由于反射地震数据采集方法具有快速横穿断面的特点, 波场随时间变化缓慢, 因此计算得到的耗散率反映了能量从大尺度向小尺度的转化速率(Sheen et al, 2009)。
在假设研究区域处于稳定剪切状态的前提下, Osborn经验公式(Osborn, 1980)可将耗散率转化成跨密度面扩散率, 且适用于湍流段和内波段:
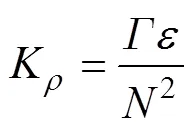
3 结果与讨论
3.1 混合参数空间分布
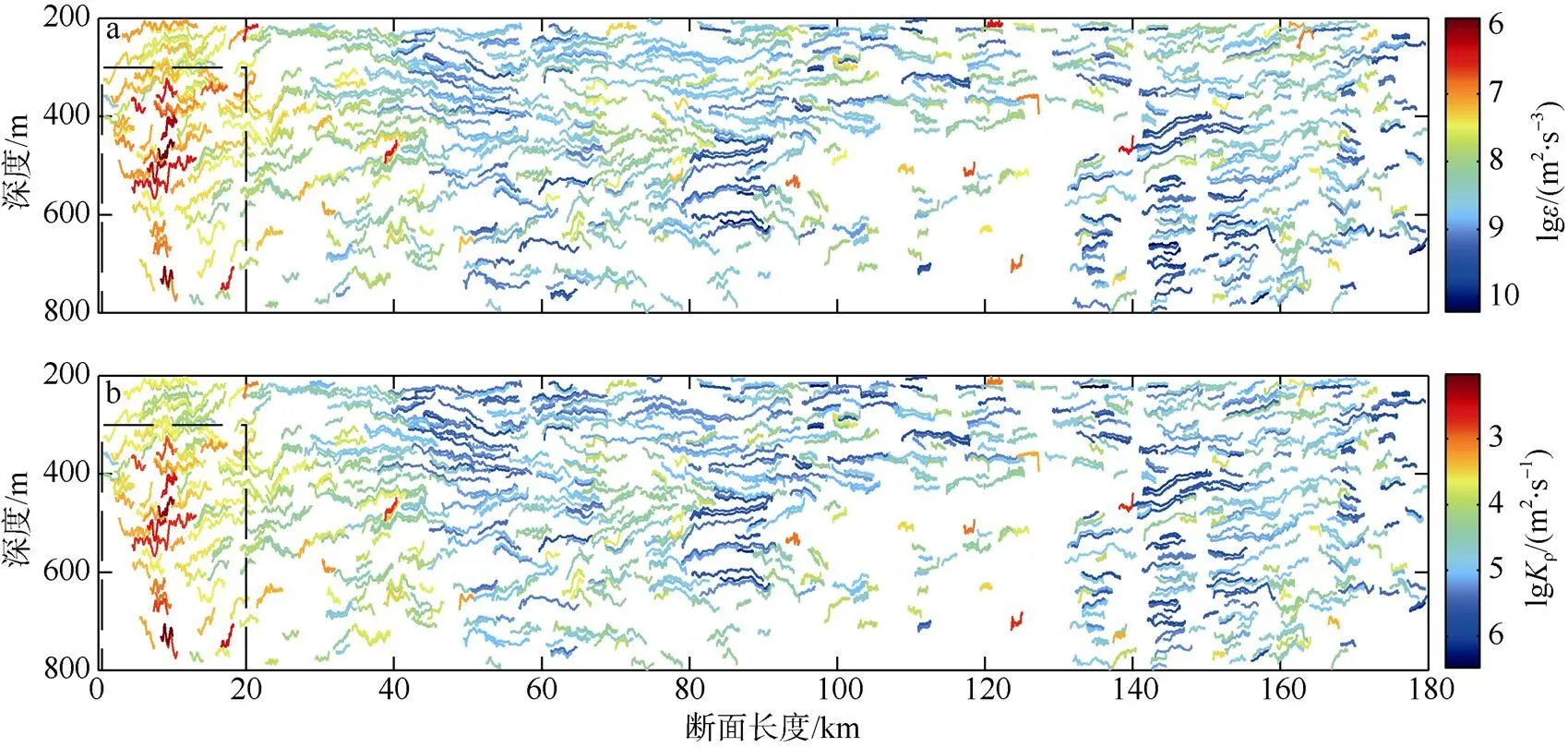
将每一条同相轴反演得到的结果填图到其所在的线段上, 得到该区域湍流段和内波段的耗散率及扩散率, 结果如图6和图7所示。研究区域的湍流段和内波段混合参数统计均值如下: 湍流段的耗散率和扩散率均值分别为8.7×10–8W·kg–1、4.7×10–4m2·s–1; 内波段的耗散率和扩散率均值分别为1.9×10–8W·kg–1、1.1×10–4m2·s–1。两段的扩散率与开阔大洋背景场相比均高一个量级以上。
本文对研究区域利用水体反射地震资料, 拾取其同相轴代替等密线, 通过斜率谱的方法计算得到该区域湍流段和内波的耗散率及扩散率。此前, 也有物理海洋学家用其他方法对南海东北部和吕宋海峡的湍流混合进行研究, 如Tian等(2009)在IWME (Internal Wave and Mixing Experiment)实验中得到该海域两个剖面的湍流扩散率。Tian等使用低频声学多普勒流速剖面仪(lowered acoustic Doppler current profiler, LADCP)、温盐深剖面测量仪(conductance temperature depth, CTD)等仪器获得剖面的流场和温盐数据, 通过参数化模型计算得到湍流扩散率, 并与垂向微结构湍流剖面仪vertical microstructure profiler, VMP)实测数据对比分析, 验证了参数化结果的可靠性。从结果上来看, Tian等在与本文地震测线相近位置上得到的湍流扩散率量级约为10–4m2·s–1, 与本文的结果相近, 表明本文计算得到的混合参数值是可靠的。
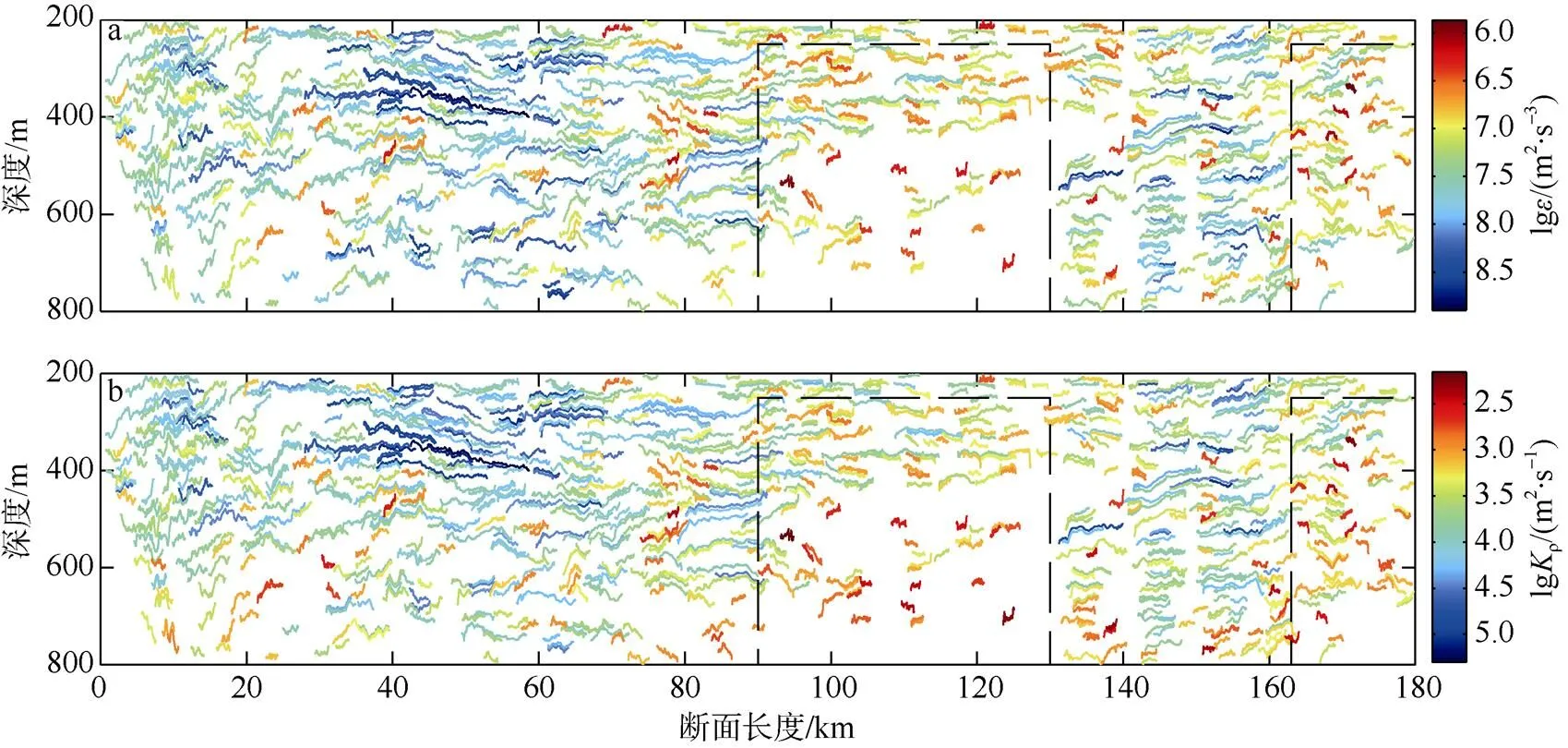
图6 湍流段计算得到的耗散率(a)和扩散率(b) 图中虚线方框内为混合强烈区域