一种改进的证据理论算法及其应用

张国栋，祁瑞敏

（郑州工业应用技术学院机电工程学院，河南新郑451100）

0 绪论

由于传统的证据理论存在与实际相悖论的问题，于是很多学者开始从事这方面的研究工作，也涌现出了许多改进算法，主要是对合成规则和融合模型进行改进，当传感器产生冲突证据时，证据理论在决策判断时失效，不能做出正确的决策。基于此，本设计提出了一种改进的证据理论处理算法，并引入了比例系数的概念，通过算法比较也验证了该方法的有效性和可行性。

矿井提升机的健康诊断主要是对提升机的健康状况进行检测和诊断[1-3]，判断系统是否健康。提升机系统主要由电动机、减速器和滚筒组成，在多个方向会安装有传感器来进行监测。由于其环境的复杂性和多变性，传感器极易受到干扰，造成误判，和实际结果相悖论，所以本设计把改进的证据理论算法应用到矿井提升机的健康诊断中，通过实例分析，该方法能准确判断矿井提升机是否健康，起到在故障发生前的监测和预警。

1 证据理论及冲突证据分析

1.1 证据理论

证据理论[4]是建立在非空集合辨识框架上的理论，其中识别框架用Θ表示，由互斥并且穷举的元素组成。

定义1：问题域的任意命题都属于辨识框架的幂集 2Θ，假如函数m:2Θ→[0,1]满足：m(Φ)=0和两个条件，则称m为辨识框架Θ上的基本概率分配函数。

1.2 组合规则

定义2：假设Θ下的证据E1,E2,…,En，对应的基本概率分配函数为m1,m2,…,mn。则D-S的合成规则：

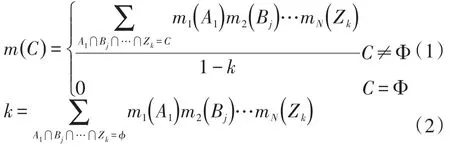
其中，k主要反映证据间的冲突程度；为正则化因子。

1.3 冲突证据分析

从式(2)看出，描述证据之间冲突程度的k值越大，两证据之间的冲突愈严重，所以把k值称为冲突因子。下面从两个例子分析：

例1有两组证据E1和E2，它们的基本概率赋值为

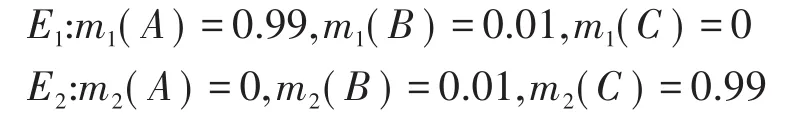
用证据理论合成规则可计算出k=0.9999，可以看出属于高冲突。从证据体中分析：证据1支持A，证据2支持C，融合结果却为m(A)=0,m(B)=1,m(C)=0，即支持了B。

例2两组证据E1和E2，它们的基本概率赋值为

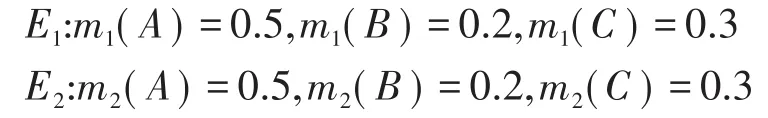
可以看出两个证据是相互支持的，不存在所谓的冲突，但计算出k=0.62，表明两个证据之间的冲突较大，显然与事实不相不吻合。所以用k来描述证据之间的冲突程度不合适。

从以上两个例子分析可知：在一定程度上k越大，表明两个证据相互的支持度越低，但并不能一概而论，它只是表示了两个证据之间的关系度，如何将其更好地加以运用是分析解决冲突问题的关键。

2 已有的改进算法

针对冲突证据的存在，很多学者从两个方面进行了研究：对合成规则和融合模型进行改进，研究如何将冲突证据加以合理利用[5-13]。

文献[5]认为冲突证据在整个融合过程中提供不确定的信息。不应该将其赋给某个焦元中，而应直接赋给未知部分。其合成结果可以解决例1（Zedeh反例）中存在的完全冲突的问题，融合结果与实际相吻合。但该方法使未知部分的基本概率赋值过大，是对冲突证据的完全否定。

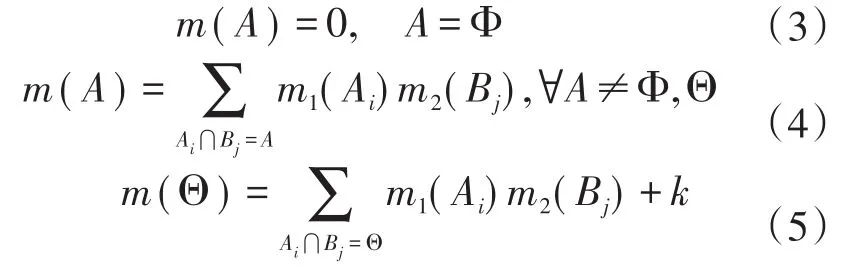
文献[6]对合成规则进行了修改，把证据间两两证据冲突程度进行平均，在解决冲突问题上比文献[5]效果好，但仍是未知部分即不确定项占主导，不能有效解决冲突问题。

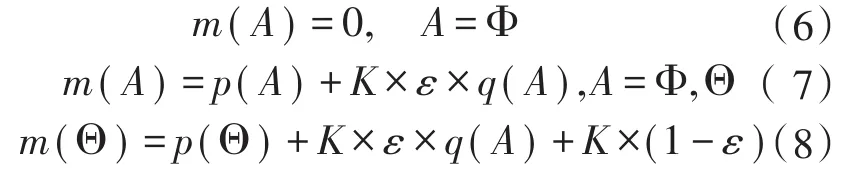
文献[8]提出融合前先对证据进行平均，然后再运用合成规则迭代运算，减少了证据间出现冲突的异常证据的作用。但该方法只是简单把证据平均，未考虑到证据间的关联，不能有效利用冲突证据。

文献[11]提出一种有效的合成规则，将冲突证据加权平均，再分配给各个证据。新的合成规则提高了融合结果的准确性，但平均支持程度未考虑各证据直接的相关性，缺乏对所有证据的整体认识。

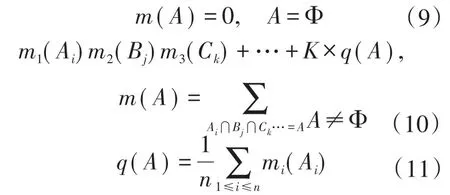
3 本文的改进算法

由于以上方法的缺陷，本文提出了改进算法，引入了证据间比例系数的概念，步骤如下：

步骤1：首先求两证据之间的冲突相量[5-8]

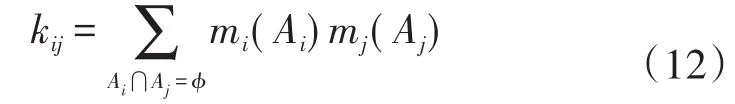
所构成的冲突矩阵为

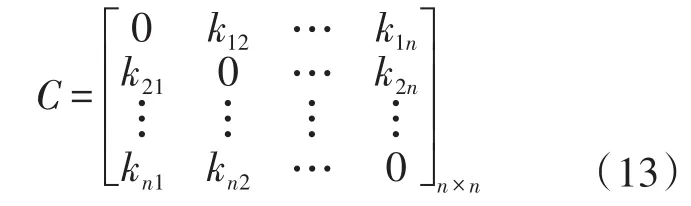
步骤2：冲突矩阵可得出[9-13]：

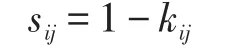
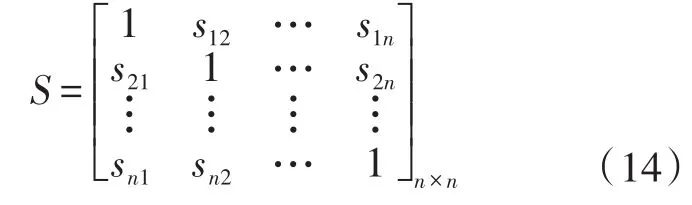
步骤3：求信任度系数

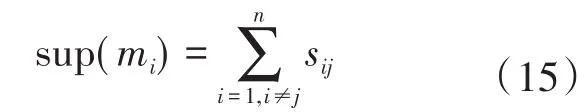
它表示某证据体被其他证据的支持程度，sup(mi)越大，表明该证据与其他证据之间的相似度愈高，即证据之间的相互支持程度就高，反之，该证据的支持程度就较低。

求各证据的权重，并将信任度系数进行归一化处理[17]：

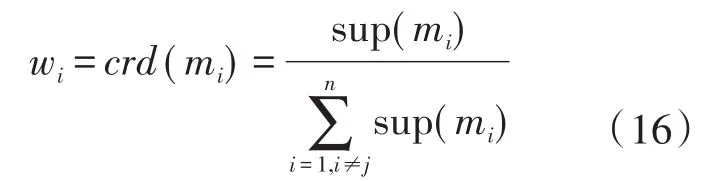
步骤4：求出各传感器所提供证据的信息熵，由于证据之间是对等，各证据所提供的信息量亦是平等的，所以不能将冲突证据舍弃，相反应该将其更准确地应用到信息融合中，需求出各证据所包含的信息量即信息熵：

步骤5：求修正冲突系数。将求得的各证据信息熵进行比较，辨识出最小值，并将其对应证据进行修正，为了保证证据体的有效性，其他证据体保持不变。本文在权衡冲突相量信息融合中作用的基础上，并充分考虑证据之间的关系，即修正系数为

步骤6：修正证据为

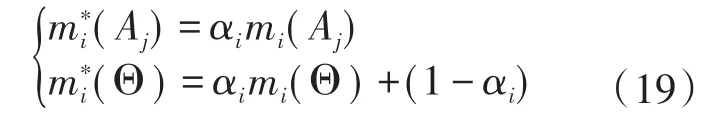
将冲突证据修正后，再用证据理论进行融合。

4 决策规则

设∃A1,A2⊂Θ满足：

甘薯淀粉与魔芋胶复配体系的糊化特征值见表2，糊化温度能够反映淀粉糊化所需要的能量；峰值粘度、最终粘度反映体系的表观粘度，该值越大说明体系的粘稠度越大；崩解值越小，表明体系的热稳定性越好；回生值越小，表明体系越不容易发生短期老化。

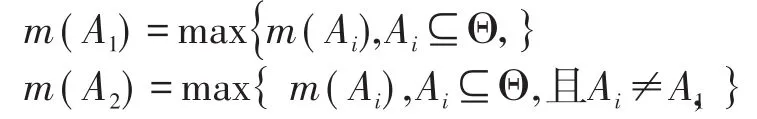
若有

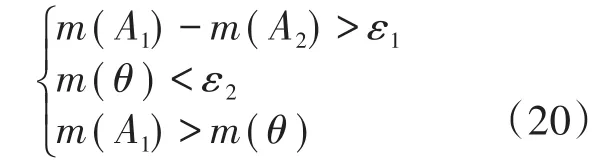
则A1即为判决结果，否则，判决结果为不确定状态。其中ε1，ε2为预先设定的门限。对于矿井提升机而言，判决结果为健康和非健康状态。

5 算法比较

以文献[11]中的2个证据为例，在某目标识别系统中，设识别框架Θ={A,}B，各证据的基本概率赋值为

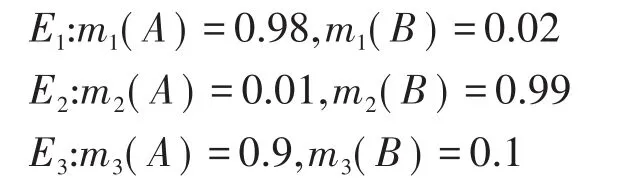
按照改进的算法式（12）～（19）进行计算，最后按照证据理论合成规则进行信息融合，融合结果如表1所示。

表1 融合结果对比表

从上表中融合结果可以发现：采用D-S证据理论最终融合结果支持证据B，显然与实际情况不相符。文献[5]对合成规则进行了修改，从融合结果中可以看出不确定性概率高达0.9990。文献[6]的不确定性仍然较多，但比文献[5]有所降低。文献[11]可以正确识别目标，而且准确率可达0.7895。本文在充分考虑证据之间关系的基础上，通过计算两证据之间的冲突相量，进而推导出证据之间的相似度，并进行加权平均，根据证据间信息熵的大小求修正系数，识别出冲突证据并进行处理，从表1可以看出第1次融合结果为m(A)=0.9789，2次融合结果为m(A)=0.9978，该方法收敛速度较快。

6 改进算法在矿井提升机健康诊断中的应用

矿井提升机系统主要由电动机、减速器和滚筒组成，在进行现场试验时，需要6个传感器分别安装在电动机、减速器和滚动的水平和垂直方向，然后测出它们的振动信号。在某一时刻的隶属度函数参考值如表2所示。

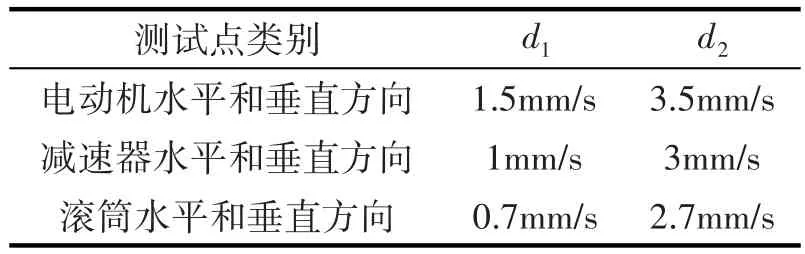
表2 隶属度函数值

在某一时刻测出振动烈度V=(V1V2V3V4V5V6)=(1.503.241.891.532.422.54)，可求出基本概率赋值如表3所示。

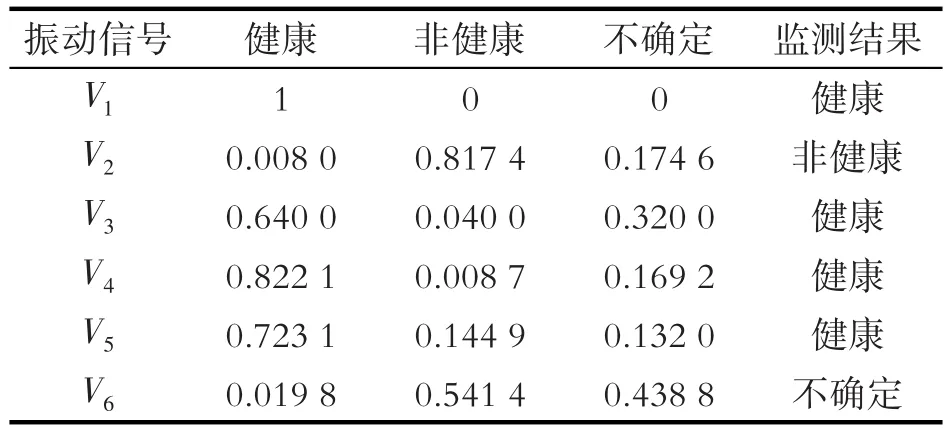
表3 基本概率赋值

从表3可以看出，只有V2提供的信息支持非健康状态，分析其主要原因是由于传感器自身的问题或者是矿井提升机所处的环境造成的，所以在信息融合时，这部分信息不能够舍去，而是想办法加以利用，所以可采用本文的改进算法进行信息融合。融合结果如图1所示。

从图1可以看出：第一次融合后输送机运行状态不确定，经二次融合后可以看出健康状态可信度较第一次有较大提高，但存在一定的目标不确定性，第三次、第四次融合后对于健康状态的可信度很高，可以判断输送机运行在健康状态，并且对目标的不确定已很小。最后根据式（20）就很容易判断出矿井提升机处于健康状态。

7 结语

本设计在比较传统的证据理论算法和本设计改进算法的基础上，分析了传统算法的不足，并得到改进算法的可行性，最后把改进的证据理论算法应用到矿井提升机的健康诊断中，通过分析证明了该改进算法的可行性。该改进算法也可以进一步扩展应用到其他诊断中，比如大型旋转机械的诊断、电子设备的诊断。

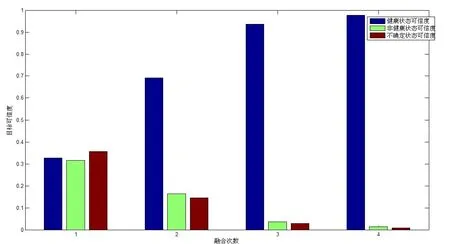
图1 融合结果图