基于均质两相流的滚动转子压缩机径向泄漏预测模型
2019-10-12王寿川张欢徐进兵李斯文
王寿川,张欢,徐进兵,李斯文
(合肥通用机械研究院有限公司,安徽 合肥 230071)
0 引言
滚动转子压缩机工作时,偏心转子紧贴气缸内壁回转,造成月牙形空间容积周期性变化,完成吸气与压缩过程。转子压缩机的结构特点决定了压缩腔密封线较长,需要大量的冷冻机油填充转子与气缸的配合间隙,防止制冷剂气体直接通过径向间隙由压缩室进入吸入室,维持高低压差,减少径向泄漏量,见图1。然而,制冷剂在冷冻油中具有一定溶解性,油-氟混合物在间隙内的流动过程中,制冷剂质量分数因压差、温度影响存在一定衰减,导致了制冷剂泄漏至低压腔,造成滚动转子压缩机容积效率下降[2]。径向间隙泄漏是制冷剂内部泄漏的主要途径,在结构间隙泄漏中占比超过85%[1]。因此,对径向间隙制冷剂泄漏量进行预测,对辅助滚动转子压缩机设计,提高容积效率有重要意义。
关于气体制冷剂泄漏量的预测模型最初采用简化模型,文献[3]通过模拟纯制冷剂的可压缩性,建立纯气体制冷剂的泄漏量预测模型,但没有考虑润滑油的密封性;文献[4]考虑径向间隙存在润滑油的情况,并通过模拟润滑油与制冷剂混合物的流动,建立了径向泄漏模型,然而模型中没有考虑制冷剂溶解度发生变化的特性,导致泄漏预测不准确。实际上,科研工作者对径向间隙内液体的流动状况进行的可视化实验结果表明[5],滚动转子压缩机正常运行情况下,径向间隙间的液体流动状况具有两个重要特征:第一,径向间隙中充满液态膜,第二,径向间隙下端存在大量微小气泡,具有两相流特征。因此,准确的径向间隙泄漏预测模型,必须考虑油-制冷剂混合物的两相流动。基于此,文献[8]提出了油-制冷剂混合物的两相流动模型,对气体制冷剂泄漏量进行预测,该模型假定流动发生在等温条件下。然而,实验表明,流体中的气泡是通过相变形成,说明混合物流动过程是在非等温条件下进行的。

图1 转子压缩机结构图
针对此,提出了含油制冷剂混合物的均质流动模型,将流动区划分为单相区和两相区,认为两相流由油-氟混合物中制冷剂“析出”形成。提出温度、压力相关的可变制冷剂溶解度,在此基础上,根据混合质量流率和制冷剂质量分数的变化情况,建立适应于各种工况下的制冷剂泄漏量预测方程。
1 径向间隙的混合物流动模型
1.1 径向间隙几何模型
图2为滚动转子压缩机径向间隙结构图。由图可知,转子中心与气缸壁之间的距离可表示为[7]:

式中,e为离心率。

图2 径向间隙几何图
由于径向间隙高度远小于平均曲率半径,而偏心距e又远小于转子半径Rp, 因此,可将圆柱坐标展开为直角坐标进行分析,如图2所示,则径向间隙高度的表达式为:

式中,Rp为转子半径。
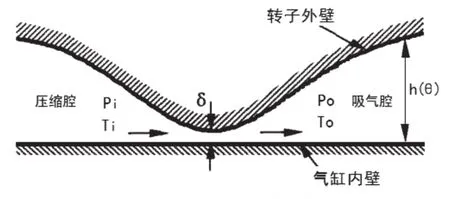
图3 径向泄漏的简化模型
1.2 油-制冷剂混合物流动的相变特性
由于压缩腔和吸气腔两端压力差造成冷媒在油中的溶解度不同,冷媒随着油由径向间隙从压缩腔流到吸气腔,压力下降,冷媒从油中“析出”产生泄漏。Gasche等[7]研究表明,混合物在径向缝隙的流动过程中温度也发生了剧烈变化,导致溶解度剧烈变化,温差变化在入口压力较高时更为明显。因此制冷剂在冷冻油中的溶解度须描述为温度、压力相关的函数
一般来说,在压缩机稳定运行时径向间隙入口压力为Pi, 温度为Ti时 ,入口处制冷剂的质量分数不会超过制冷剂在油中的溶解度此时混合处中制冷剂处于欠饱和状态,此时制冷剂质量分数在入口处是恒定的,但随着混合物的摩擦流动,混合物温度升高,压力下降,导致制冷剂的溶解度下降,当达到临界值Pcr,Tcr时 ,制冷剂的质量分数和溶解度相同,即

1.3 最小间隙混合物流动模型
对混合物流动进行建模时,忽略体积力、惯性效应,非流动方向的压力梯度,不考虑滚动转子滑移,则间隙内混合物流动的连续性、动量和能量方程如下:
上述模型中,入口压力Pi,温度Ti是给定的。利用方程(8)计算局部压力梯度需要两个物理参数:混合物的密度和绝对粘度(或运动粘度),这两个参数值与混合物的流动状态(单相流动或多相流动)密切相关。
1.3.1 单相流区域参数计算
单相流动中,参考ASHRAE手册(2010),均质理想混合物的流体密度计算公式为:

而动力粘度可根据各组分动力粘度曲线由Matlab 拟合得出动力粘度与温度、压力的方程,计算得出[9]。
由于液体的焓值只与温度有关,而单相流动下密度变化较小,据式(6)分析可知单相流动区域能量方程的计算结果是一个近似恒定的温度。因此,单相流动区域流动发生于等温情况下。
1.3.2 两相流区域参数计算

由于油的蒸气分压较低,气相通常仅由气态制冷剂组成,故气相密度即为该状态下制冷剂的密度,相关信息可由Coolpack软件获取。
Dukler等[10]提出均相粘度的计算公式为:

式中,x为两相混合物流体中气体质量分数,Vv和Vl分 别为气相和液相的比体积,和分别为气相和液相的动态粘度。
若液态部分一直为饱和态,由制冷剂质量守恒可知:
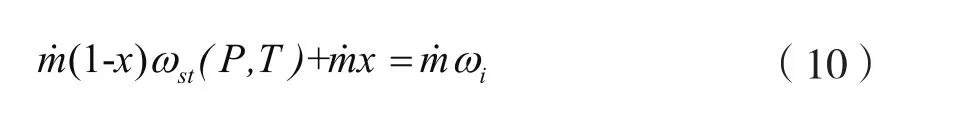

2 制冷剂泄漏量预测
设涡旋压缩机的尺寸参数:转子半径为21.1mm;气缸半径为23.0mm;以及转子宽度为27.0 mm。在给定入口压力Pi,温度Ti条件下,利用欧拉法,可计算得出流场分布。本算例以R134a-酯类油混合物为例,缝隙入口处制冷剂在油中溶解饱和度为0.9。
在吸气压力为100kPa时,计算得到缝隙进、出口各个压力比条件下,径向间隙混合物质量流量。结果如下图4所示。

图4 出口流量与前后压力关系
可见,在间隙高度一定的条件下,随着压力比的增高,混合物流量增大。且增大幅度随着间隙高度的增加而更加明显。
图5给出了间隙分别为30μm、 40μm、50μm时,混合物流量与压力比关系图,可以看到,在压力比介于1.0至4.0之间时,随着压力比升高,油-氟混合物质量流量迅速增加,在压力比大于4.0后,增幅开始减弱。在间隙高度较小时,该趋势越早出现。该结果与辛电波等[11]关于细小通道的油-氟两相流的实验研究结果相似:对于特定宽度的通道,压力比超过一定值后,流量增加幅度减缓。在缝隙高度小于30μm时,油-氟混合物流量在压力比超过4.0后几乎没有变化。

图5 间隙混合物流量与压力比关系
图6是制冷剂泄漏量与压力比、间隙高度的关系图。可以看出,泄漏量与间隙高度成正比,在间隙超过20μm后,泄漏量迅速增加。在间隙高度一定时,压力比小于4.0时,制冷剂泄漏量随压力比升高而增加;压力比介于4.0至5.0之间时,制冷剂泄漏量随压力比升高而小幅减少;压力比超过5后,制冷剂泄漏量又随压力比增加而增加。分析可知,这有两方面的原因:一方面,压力增加对溶解度降低起到了减缓作用;另一方面,压力比超过4后,流量增加幅度减缓,相变作用导致的冷却效果增加了气体的溶解度。

图6 径向间隙泄漏量与压力比关系图
图7和图8分别给出了动态运转下,容腔压力和气缸温度(壁面温度)分布与转子转角(滑片位于最上端时,角度为0)的关系。

图7 转子压缩机典型的压力曲线

图8 转子压缩机典型的气缸壁温度曲线
为验证模型在压缩机整个吸气、压缩、排气压缩过程中的预测准确性,利用本模型对算例中压缩机的各点的泄漏量进行计算。考虑到混合物液膜流动较薄,本文采用壁面温度为缝隙进口温度;入口压力为压缩腔压力;出口压力设为100kPa;入口混合物中制冷剂溶解饱和度为0.9。
计算可得制冷剂泄漏量与转角分布关系,如图9所示。随着转子旋转,压缩腔压力升高,温度增加,制冷剂泄漏量迅速增加,排气中段,制冷剂径向泄漏量反而有一定幅度减少;排气末段,制冷剂泄漏继续增加;排气至最小余隙容积处,泄漏量迅速降低。
分析可知,压缩机压缩腔到排气压力后,排气阀打开,压缩腔压力基本处于稳定,此时混合流量处于稳定状态,而壁面温度(即缝隙入口温度)继续上升,入口制冷剂的质量分数下降,缝隙出口处制冷剂泄漏量随之下降。本文结果,与KIM等[12]的CFD计算结果具有相同趋势,说明可信度较高。
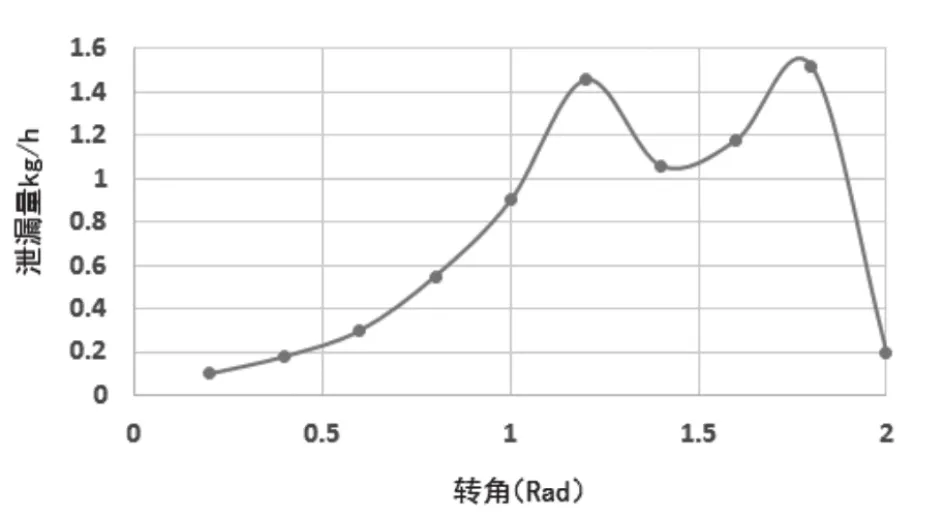
图9 径向间隙泄漏量分布
3 结论
从可变溶解度角度出发,解释了制冷剂-冷冻油混合物中制冷剂的“析出”过程,并形成了描述均质两相流的数学模型,利用该模型对10-50μm径向间隙的制冷剂泄漏情况进行了计算验证。结果表明:
1)随着间隙进、出口压比增加,间隙内混合物质量流量开始增加,但压力比超过4.0后,流量增加幅度随着压力比增加而减弱。在缝隙高度小于30μm时,流量在压力比超过4.0后几乎没有变化。
2)径向间隙的制冷剂泄漏量随着压力比增加而增加,压力比4.0至5.5之间时,缝隙出口制冷剂泄漏量反而一定程度减少,这是出口处溶解度增加而混合物流量增幅降低导致的。压力比超过5.5后,制冷剂泄漏量恢复随压力比升高而增加的趋势。
3)转子压缩机在排气过程的中段,排气压力稳定,由于气缸壁面即缝隙入口温度继续增高,导致油-氟混合物制冷剂溶解度下降,制冷剂径向泄漏量有一定程度的减少。
本文在于现有文献的对比中,取得了类似的结果,而在几何建模和数值计算工作量上具有一定优势,同时得出了制冷剂泄漏量随转角的变化趋势,对转子压缩机的设计有较大参考价值。
