基于ECC算法在数字签名中的分析与研究

李雨 张俊

摘   要：数字签名是保证信息完整性和认证性的关键技术，设计出一种高效性、安全性的数字签名方案尤为重要。文章分析并研究了数字签名的方案，重点研究了各方案的优缺点，提出了一种基于ECC数字签名算法方案，能有效提高数字签名的安全性和稳定性。

关键词：数字签名;ECC;高效性;安全性;稳定性

随着计算机网络信息化的快速发展，安全、高效、完整地传输信息变得越来越迫切，要求也越来越高。因此，信息安全已成为当今社会重点关注的问题。

数字签名是解决现代信息安全问题的关键技术之一，能实现用户的身份认证，具有数据完整性以及不可抵赖性等特点。目前，常见的有RSA签名方案、DSA签名方案、ElGamal签名方案等。这些主流签名方案在计算效率、安全性、密钥长度等方面还有待提高。针对以上问题，本文提出了一种基于ECC的数字签名方案，旨在提高数字签名的安全性和计算效率。

1    ECC算法

ECC算法是以一种加密公开密钥的方法为基础的椭圆曲线[1]（Elliptic Curves Cryptography，ECC），椭圆曲线是一个三次方程（Weierstrass方程）[2]：y2+a1xy+a3y=x3+a2x2+a4x+a6，令：

代入Weierstrass方程可得：

当Z≠0时，可得：Y 2Z+a1XYZ+a3YZ2=X3+a2X 2Z+a4XZ 2+a6Z 3，从中可以得出（x，y）和（x，y，z）相互呼应，并且在非零区间内的任意常数λ（x，y）（x，y，z）（λX，λY，λZ）相对呼应，这些点在同一条线上。

位于有限域上的椭圆曲线是有限的、单独的点，而不是一条不断的曲线。对于计算固定区域GF（q）中椭圆曲线的点用Hasse定理[3]：假如位于椭圆曲线上的点E是在GF（q）上，E上的点N属于（x，y）∈GF（q）范围，那么成立。有限域椭圆曲线的点的加法和实数域椭圆曲线上的点的加法的运算等同，不过在除法运算中，是用求模逆元来替换，而其他算法都在域中进行。

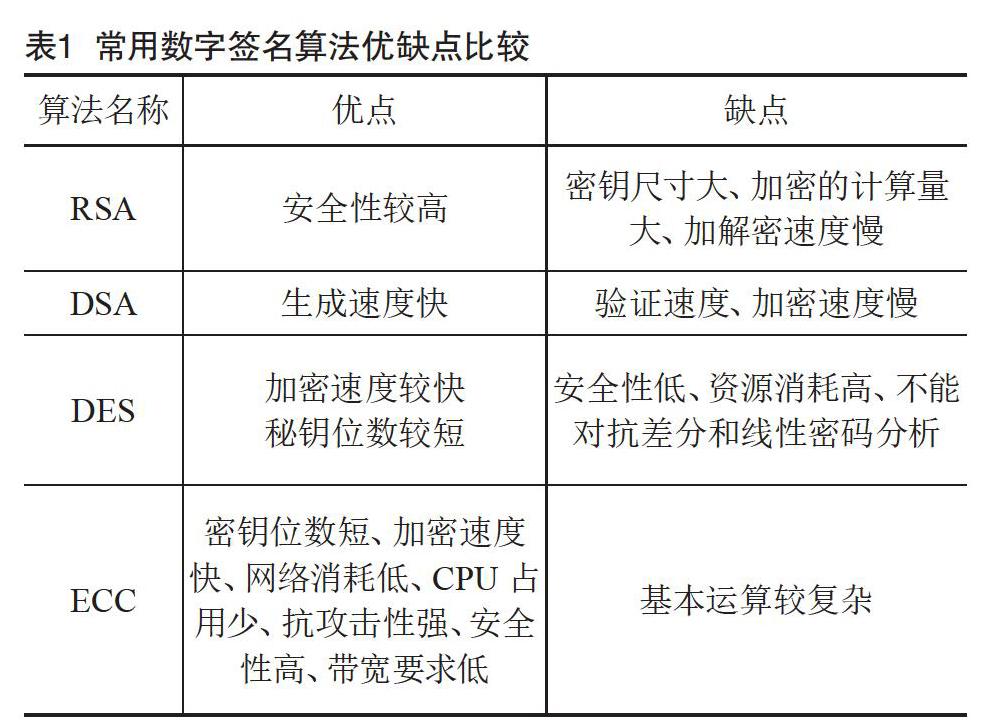
常见的签名方案有：RSA签名方案、DSA签名方案、ElGamal签名方案等，这几种常用的算法进行优缺点的比较分析如表1所示。

自公钥密码问世以来，提出了许多种公钥加密方法，它们的安全性都是基于复杂的数学难题。根据所基于的数学难题来分类，目前有以下3类系统被认为是安全和有效的。

（1）大整数因子分解系统（代表性的有RSA）。

（2）有限域（数学中的一种代数结构）离散对数系统（代表性的有DSA）。

（3）有限域椭园曲线离散对数系统（ECC）。

其中，有限域椭园曲线离散对数系统相比另外几种系统更安全，算法运算速度更快。所以就可以基于ECC算法得到一种更安全的数字签名方案。

2    基于ECC数字签名方案

ECC数字签名方案利用椭圆曲线标量乘、点加等运算，以及有限域的模运算法则，实现快速的数字签名和签名验证，是一种建立公开密钥加密的算法，基于椭圆曲线数学的数字签名方案。签名与验证的运算基本都在有限域进行，避免了耗时的模归约运算。该数字签名方案可用于电子商务、内容保护接口、银行系统、军事通信、知识产权保護等环境中。

在使用数字签名时，发送方通常先对消息生成一个生成元，再利用私钥对生成元进行签名，接收方收到消息及签名时，也先对消息生成一个生成元（与发送方使用同种单向函数），利用发送方发的公钥、签名以及自己的生成元进行签名验证。

实际应用中，由于直接对原消息进行签名有安全性问题，而且原消息往往比较长，直接使用RSA等算法进行签名速度会比较慢，所以一般对消息会使用ECC算法进行签名计算。只要使用的ECC算法是安全的，那么这种方式的数字签名就是安全的。

在ECC中，设Eq（a4，a6）为椭圆曲线上的由理点构成的Abel群，G为椭圆曲线上的一个循环子群，P是G的一个生成元，Pm为椭圆曲线上的点。

2.1  在Eq（a4，a6）上Diffie-Hellman的ECC签名方案

签名的步骤描述如下。

（1）找出q≈2180和两个参数a4和a6。

（2）公开参数是G和Eq（a4，a6）。

（3）从用户A中选择私钥nA。

（4）在Eq（a4，a6）上选择一个公钥传送给用户B。

（5）用户B选择私钥nB和公钥PB，把PB发送给用户A。

（6）用户A，B形成共同密钥k 。

攻击者想得到k，就必须计算出nA，亦或是PB和G计算得到nB，所以必须计算出椭圆曲线的离散对数[4]。

2.2  在Eq（a4，a6）上Massey-Hellman的ECC签名方案

在Eq（a4，a6）上Massey-Hellman[5]的ECC签名方案签名的步骤描述如下。

（1）选择密钥eA，0≤eA≤N。

（2）计算dAeBeAPm=eBPm。

（3）计算eAPm。

（4）计算dAeBPm=Pm。

（5）dAeBPm=Pm对在计算中复原。

最后，签名者就可以把信息Pm迅速发送给接收者。

2.3  在Eq（a4，a6）上ElGamal的ECC签名方案

在Eq（a4，a6）上ElGamal[6]的ECC签名方案签名的步骤描述如下。

（1）选择椭圆曲线得到Eq（a4，a6），对明文进行算法编码而形成点Pm。

（2）选取Eq（a4，a6）和它的一个生成元G为公开参数。

（3）選取nA作为私钥。

（4）选取PA=nAG作为公钥。

（5）加密：设k为正整数，密文为Cm=kG，Pm+kPA。

（6）解密：Pm=kPA-nAkG=Pm。

3    结语

本文分析并研究了数字签名的方案，重点分析了各方案的优缺点，提出一种基于ECC数字签名算法方案，为提高数字签名的安全性和稳定性提供了参考价值。

[参考文献]

[1]王起月.基于椭圆曲线的数字签名算法研究[D].洛阳：河南科技大学，2018.

[2]冯晋光，赵志刚.网络安全中的数字签名技术分析与应用[J].电子技术与软件工程，2015（23）：225.

[3]余杜鹃，曹炜.有限域上一类方程的解数[J].宁波大学学报（理工版），2014（1）：66-69.

[4]冯阳.基于超椭圆曲线密码体制群签密系统的研究[D].贵阳：贵州大学，2015.

[5]RAVI K B，CHANDRA S A，APPALA N G.An elgamal encryption scheme of fibonacci q-matrix and finite state machine[J].Journal of Applied Computer Science&Mathematics，2015（20）：9-10.

[6]冯泽波，吴晓平，任伟.关于ElGamal加密和签名方案的启发式分析[J].信息网络安全，2014（5）：10-14.

Analysis and research of digital signature based on ECC algorithm

Li Yu， Zhang Jun*

（Panzhihua University， Panzhihua 617000， China）

Abstract：Digital signature is the key technology to ensure the integrity and authentication of information， and it is particularly important to design an efficient and secure digital signature scheme. In this paper， the scheme of digital signature is analyzed and studied， and the advantages and disadvantages of each scheme are studied emphatically， a scheme based on ECC digital signature algorithm is proposed， which can effectively improve the security and stability of digital signature.

Key words：digital signature; ECC; efficiency; security; stability