湖南省衡山不同海拔高度土壤的入渗特征

刘 瑞， 夏卫生， 梁羽石， 童星星， 黄道友

(1.湖南师范大学 资源与环境科学学院, 湖南 长沙 410081; 2.中国科学院 亚热带农业生态研究所, 湖南 长沙 410125)

山地土壤入渗性能研究是评价植被涵养水源和保持水土功能的基础，探究山坡林地土壤水分入渗规律对了解土壤侵蚀防治、林地地表径流流产调洪和土壤蓄水机制具有重要意义。森林土壤水库具有不占地、不垮坝、不怕淤、不耗能、不需要特殊地形、库容大、下泄快等优点[1-2]。研究山坡林地的入渗性能有利于深入了解森林水库的土壤蓄水能力，以及调蓄径流、削洪补枯的运行机制，能为改善和充分调用森林土壤水库，提高森林保水保土和防洪减灾能力提供科学依据。其中土壤水分入渗过程和渗透能力决定了降水过程的水分再分配中渗入土壤中的水量，进而影响了土壤的蓄水能力及容量，因此土壤入渗率既是评价土壤调节水分和涵养水源的重要指标，也是影响地表径流和土壤侵蚀的重要因素。土壤入渗是一个非常复杂的过程，其性能受土壤初始含水率、有机质、团聚体等土壤理化性质影响较大[3-4]，且在不同海拔高度存在较大差异。目前国内外已有诸多学者致力于土壤入渗性能的研究，也有很多研究和测量土壤入渗的方法，如点源入渗法[5]、双环法[6-8]、单环法[9]、人工模拟降雨法[10-11]、填装土柱法[12-15]等。李卓[16]等通过人工改变土壤颗粒级配设置不同容重土柱测量入渗率，结果表明容重对土壤入渗能力有较大影响。刘目兴[17]等在三峡山地测量利用盘式张力入渗仪测量土壤入渗率，其结果表明不同垂直带在土壤入渗性能上存在一定差异。莫斌[18]等人在紫色土坡耕地运用点源入渗法、双环法、环刀法对入渗性能进行对比试验，其结果证明了点源入渗法在当地有较好的应用性。在以往的研究中，大多数对试验点的土壤层造成严重破坏或者直接利用填装土柱进行室内试验，很少能够对整个山体不同海拔高度区域的入渗速率的进行探索。衡山作为中亚热带最具代表性的山地，1 000 m以下为湿润富铁土，1 000 m以上为常湿淋溶土[19]，土壤垂直带谱明显，对衡山的入渗性能进行研究对中亚热带山坡林地有重要指导意义，但在衡山上的入渗研究较少。研究拟以点源入渗法测量土壤入渗性能，此法对试验点土壤层不会造成严重的破坏，且经过改良后的点源入渗法测定土壤入渗率与双环法相比有精确度高、省时和省水的优点，更加适合野外山坡林地的测量[20]。在衡山选取不同海拔高度区域的9个试验点测量各试验点的入渗性能，利用入渗公式拟合实测结果，确定适用于衡山的最优入渗公式，探究衡山不同海拔区域土壤入渗性能特征及其影响因素，为山体大尺度上入渗性能研究提供新思路和新方法。

1 研究区与材料方法

1.1 研究区概况

南岳衡山自然保护区(27°2′—27°22′N,112°32′—112°58′E)位于湖南中部，湘江谷地，属于中亚热带季风湿润气候，其山麓海拔82 m，最高峰祝融峰1 300 m，相对海拔1 200 m。由于海拔高低相差大，垂直地带性明显，其地带性土壤为红壤，因受自然因素与人类活动等影响，土壤类型明显增多，从山麓到山顶土壤的分布规律为红壤—黄红壤—黄棕壤。

1.2 材料与方法

试验采用点源入渗测量仪测定衡山不同海拔高度土壤入渗性能。点源入渗测量仪由恒定供水装置、摄像装置和计算机系统三部分组成，恒定供水装置是由转速控制器、导管和盛水器组成。用一根橡皮导管连接盛水器和转速控制器，调节转速控制器的转速，使得控制器推动导管引出盛水器中的水。其水流流量可以根据转速计算得出：

(1)

式中：q——供水流量(ml/h)；v——转速(r/min)。

本次试验供水流量条件为模拟大雨情况(雨强2.4 mm/h)，设定供水装置转速25 r/min，水流流量为863.5 ml/h，拍照时间为5 min一帧，共9帧45 min。选取不同海拔高度的9个试验点进行的入渗性能测量试验。在试验点附近采集地表10 cm土壤带回实验室分析土壤理化性质。使用环刀法测量容重和含水率[21-22]，密度计法测量土壤机械组成[23]。使用重铬酸钾氧化法测量土壤有机质含量[24]，运用湿筛法测量水稳性团聚体，用GPS确定各试验点海拔和经纬度，其地理范围为27°15′36″—27°17′34″N，112°40′48″—112°43′15″E，各试验点土壤理化参数详见表1。

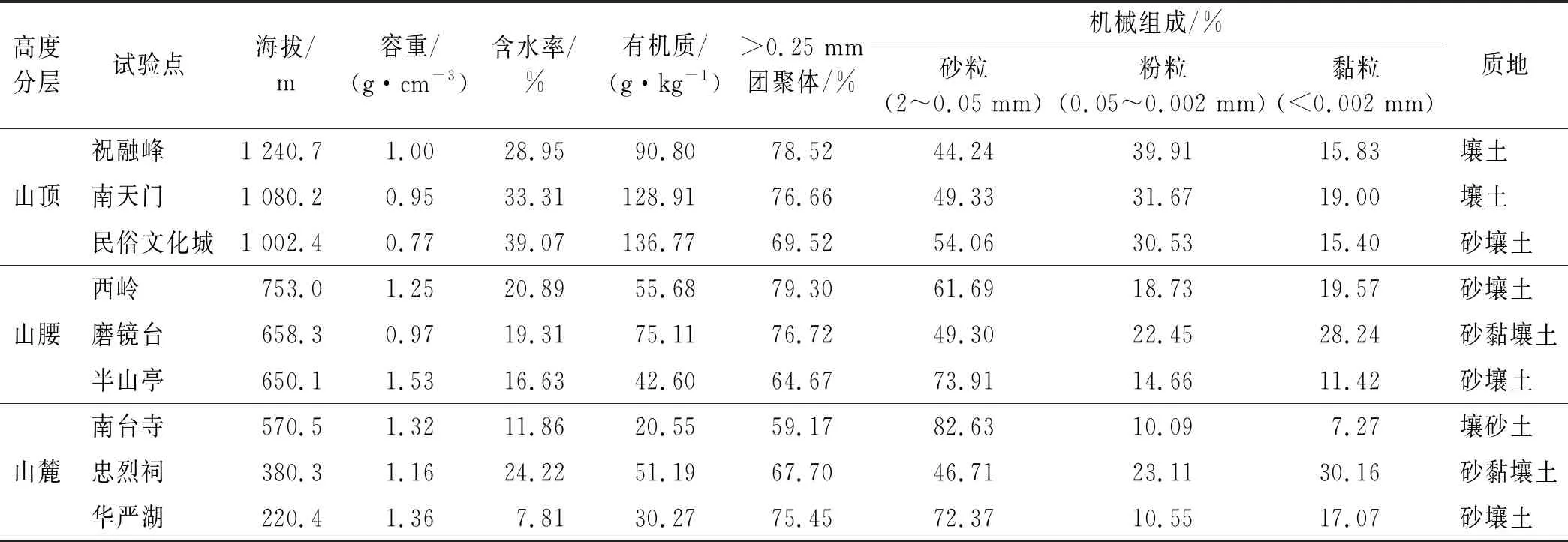
表1 研究区各试验点土壤理化参数

1.3 数据处理

因不同海拔高度土壤理化性质存在一定差异，为探究影响衡山土壤入渗性能与土壤理化性质之间的相关性，拟采用SPSS软件将不同海拔高度土壤的理化性质与各个试验点入渗率进行相关性分析。同时为探究不同海拔高度上入渗性能的差异，将9个试验点依据其海拔分为山麓(200～600 m)、山腰(600～1 000 m)、山顶(1 000～1 240 m)。用SPSS进行入渗模型拟合。3种常见的土壤水分入渗模型如下。

(1) Kostiakov模型。

f(t)=at-b

(2)

式中：f(t)——入渗速率(mm/min)；t——入渗历时(min)；a，b——拟合参数。

(2) Philip模型。

f(t)=0.5St-0.5+A

(3)

式中：A——稳渗率(mm /min)；S——土壤吸水率。

(3) Horton模型。

f(t)=fc+(f0-fc)e-kt

(4)

式中：fc——稳定入渗率(mm/min)；f0——初始入渗率(mm/min)；k——常数。

2 结果分析

2.1 衡山土壤入渗性能特征分析

土壤入渗过程是供给水在重力势的作用下由地表向土壤转化的连续性过程，对其进行探讨有助于正确认识土壤入渗的本质，也是充分评价其入渗性能的先决条件。不同海拔高度区域土壤源于周围环境因子影响致使土壤内部构造存在较大差异，因而影响土壤入渗过程，导致入渗性能存在一定差异。初始入渗率、稳定入渗率、平均入渗率和累积入渗量是评价土壤入渗中最常用的指标[25]。以试验开始后的第5 min时的入渗率为初始入渗率，稳定入渗率为土壤入渗达到稳定值时的入渗率。累积入渗量取第5～45 min的渗透总量，平均入渗率为第5～45 min的平均入渗率。总体来看，各试验点的入渗速率变化明显，且不同海拔高度区域的入渗率差异显著，但入渗过程有相同的规律。从表2可以看出，在各试验点中，初始入渗率最大值为45.2 mm/h，最小值为9 mm/h，稳定入渗率最大为14.3 mm/h，最小为3.1 mm/h，从入渗开始到稳定入渗减小了50%～86%，表现出初始入渗率>平均入渗率>稳定入渗率的特征。选取祝融峰、西岭和忠烈祠作为山顶、山腰和山麓的代表点位描述不同海拔区域入渗速率变化过程(图1)。从入渗率大小来看，表现为：山顶>山腰>山麓(表3)，稳定入渗率随海拔上升逐渐增大；从其变化趋势来看：土壤入渗过程在前10 min入渗率均呈快速减小的趋势，10～30 min呈现出缓慢减小的趋势，最终在30 min后基本趋于稳定，这是因为在入渗开始阶段，野外土壤处于非饱和状态，含水量未达到最大值，当水供应到土壤表面时依靠重力势很快进入土壤孔隙中，此阶段入渗速率较大，随着入渗的推进，孔隙被水分填充，导致土壤入渗率迅速减小，当土壤含水量达到最大后含水量不再增加，入渗水流呈饱和稳定流，入渗率趋于稳定。与前人的研究结论一致[26]。因此，在运用点源入渗法测量山地入渗一般只需要30 min左右就能测量其完整的入渗变化过程，较其他方法更加省时。

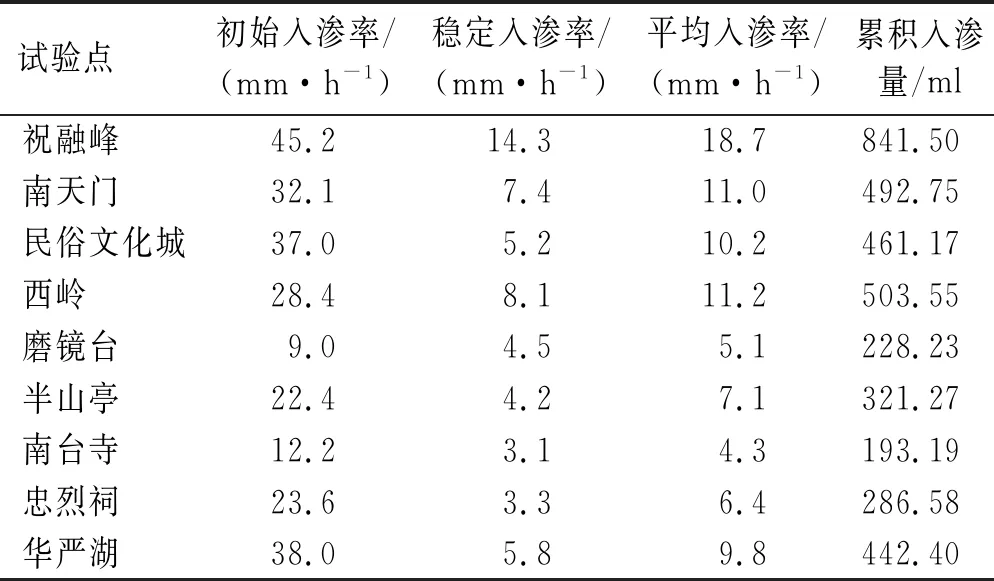
表2 研究区各试验点土壤入渗性能指标

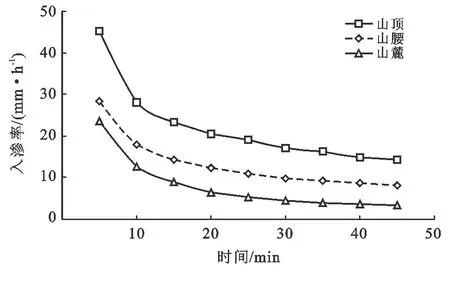
图1 研究区不同海拔土壤入渗过程曲线

表3 研究区不同海拔土壤性质对比

2.2 衡山土壤入渗影响因素分析

土壤入渗性能受容重、质地、水稳性团聚体和有机质含量等土壤理化性质影响较大[27]。在不同海拔高度区域的土壤质地、容重、有机质含量、>0.25 mm水稳定团聚等理化性质有较大差异。土壤质地通常由黏粒、粉粒、砂粒的百分比来表征，不同质地的土壤由于各种矿物颗粒所占比例不同和粗细状况不同，使得土壤保水、透水性能差异很大。将各试验点土壤理化性质与其入渗性能用SPSS软件分析得到其相关性，结果详见表4。

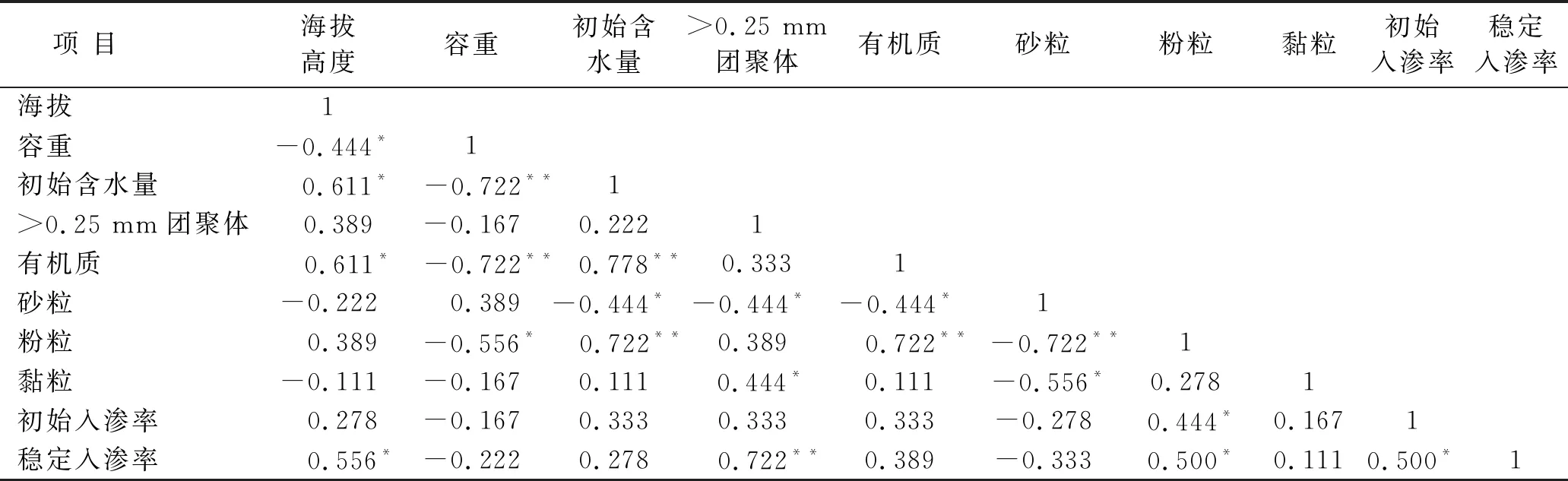
表4 研究区土壤性质相关性分析

注：*表示在0.05水平相关性显著；**表示在0.01水平相关性显著。

由表4可知，不同海拔高度区域土壤入渗性能与其土壤理化性质相关性系数差异较大，因此其影响权重有较大差异，初始入渗率与海拔高度、>0.25 mm水稳性团聚体、土壤容重、有机质含量、初始含水量、土壤质地存在相关性，但相关性较低。稳定入渗率与海拔高度、>0.25 mm水稳性团聚体、有机质含量、含水量和土壤粉粒和黏粒含量呈正相关，其中与海拔高度显著正相关，稳定入渗率随海拔升高而增大。此外稳定入渗率还与>0.25 mm水稳定团聚体呈极显著正相关关系，其原因在于>0.25 mm水稳性团聚体在土壤中能够形成良好的结构，使土壤表面更加疏松，更有利于水分入渗，其团粒结构不仅在能土壤内形成大量的孔隙，使土壤通气透水性得到有效的改善，还能增强土壤结构的稳定性，防止土壤结皮进而影响水分入渗[28-30]。而>0.25 mm水稳性团聚体与有机质和黏粒含量呈正相关，这是因为有机质在团聚体形成过程发挥着胶结剂的重要作用，黏粒则由于粒径较小更加容易被吸附。试验点土壤砂粒含量较高，砂粒平均含量为59.36%，其中山麓平均砂粒含量为67.24%；山腰为61.61%，山顶为49.21%。山麓、山腰和山顶土壤容重分别为1.28，1.25和0.9 g/cm3，其原因在于随着海拔上升，有机质含量逐渐增多，砂粒含量逐渐减少，粉粒和黏粒含量增加，导致土壤容重有逐渐减小的趋势[31,33-34]，而土壤容重越大，土壤孔隙度越小，渗透能力越弱；容重越小，土壤孔隙度越大，土壤入渗速率越大[32,35]，可见，土壤水分入渗是一个由多个因素共同影响的复杂过程。在衡山入渗试验中，稳定入渗率受>0.25 mm水稳性团聚体和海拔高度因素影响较大，而受有机质、土壤容重和质地影响较小。

2.3 土壤入渗过程模拟及其参数分析

不同的入渗公式有不同的侧重点，选择最适用于研究区的入渗公式是了解当地入渗过程的基础[40]。选取Kostiakov入渗模型[41]、Philip模型[42]和Horton入渗模型[43]，通过对比选择合适的模型参数反映土壤入渗的特征(表5)。

(1) Kostiakov模型。Kostiakov入渗模型中的参数a代表第一个时间段内平均入渗速率，a值的大小与初始入渗速率呈正比，其拟合结果与实测初始入渗率的大小顺序一致，说明拟合与实测偏差较小；b值为经验入渗指数，反映了入渗能力衰减速度，b值的大小与入渗能力衰减速度成正比，其均值表现为：山麓>山顶>山腰，山麓比山顶和山腰能更快的达到稳定入渗状态。尽管Kostiakov模型是经验模型，但使用该公式较简便而且较为准确。

(2) Philip模型。Philip模型中，参数S是反映土壤入渗能力大小的指标，S值越大，入渗能力越强。S的平均值最大值在山顶(85.92)。表明山顶入渗性能最好。A表示的稳定入渗率，拟合结果均为负数，使其物理意义不明确，所以认为Philip模型描述该区域土壤入渗特征有一定局限性。

(3) Horton模型。Horton模型拟合中，参数f0代表的初始入渗率，模型拟合反映的情况与实测值有一定差异，参数fc代表稳定入渗率，均值表现为山顶>山腰>山麓，与实测值大小顺序一致，反映出不同海拔区域的稳定入渗率的分布特征；常数k决定着入渗率减小的速度，k值越大，越快达到稳定入渗状态，其均值表现为：山麓>山顶>山腰，与上述Kostiakov模型反映的规律一致。从各参数代表的物理含义上来看，Horton模型反映了衡山不同海拔区域土壤的入渗性能特征，稳定入渗率大小顺序为：山顶>山腰>山麓。

由表5和上述分析可知，各模型在试验点的决定系数R2均高于0.95，均能较好模拟出水分向土壤中入渗的过程，除Philip模型难以适用于衡山外，采用的另外两个模型都适用于衡山土壤入渗。其中Kostiakov模型反映入渗速率的衰减速率，Horton模型则能够较好的反映出衡山土壤入渗性能大小的分布特征。从相关系数R2的大小而论，Kostiakov模型拟合结果相关系数R2均平均值较大(0.995)，而Horton模型较小(0.992)。所以认为Kostiakov公式模型拟合效果最好，Horton模型较差。因此认为在衡山入渗过程的模拟中Kostiakov模型中最为适用，说明点源入渗法在山坡林地有较好的适用性。

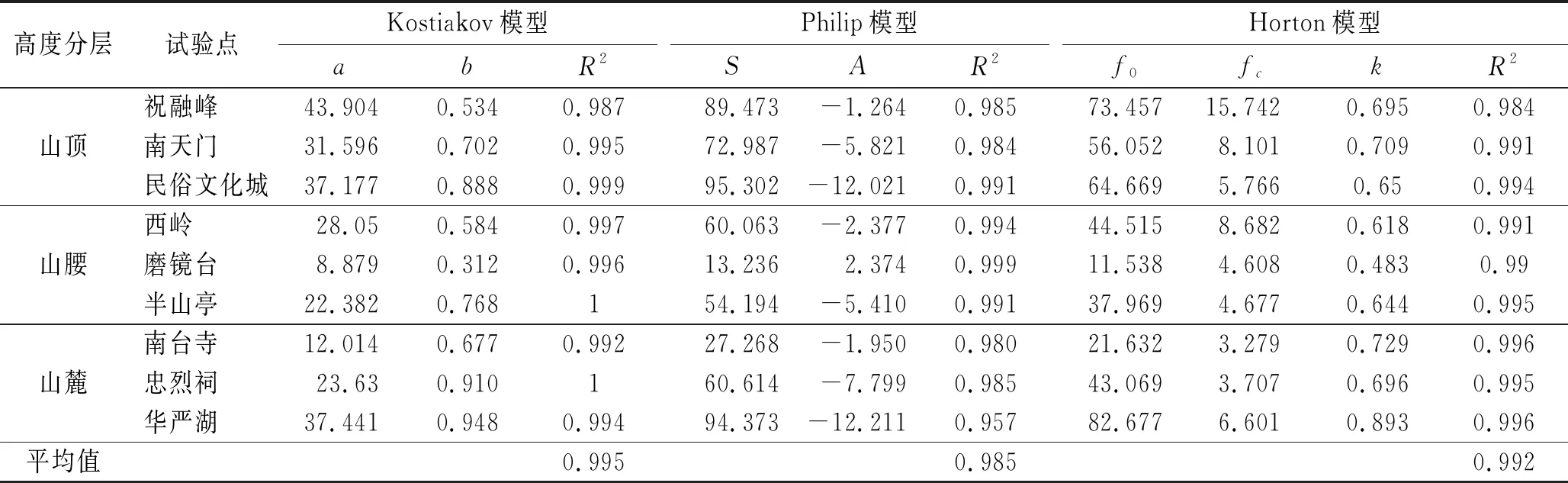
表5 研究区不同入渗公式模拟比较

注：R2代表模型决定系数；a，b为Kostiakov模型的参数；S，A为Philip模型的参数；f0，fc，k为Horton模型的参数。

3 讨 论

通过在衡山选取的9处试验点进行点源入渗性能测量试验，结果显示稳定入渗率在整个衡山范围内随海拔升高而逐渐增大。已有研究[36-39]表明在一定海拔范围内，土壤容重、有机质含量、土壤各粒级含量有随海拔变化的趋势，如刘目兴[17]在三峡山地区域的研究结果表明土壤容重和砂粒含量随海拔上升逐渐减小、有机质含量随海拔上升逐渐增加，且入渗率也随海拔上升有增大的趋势。但也有学者有不同的结论，如李志等[44]对同处亚热带地区的武功山进行土壤入渗性能研究，其稳定入渗率有随海拔升高逐渐先减小趋势，两者趋势不同的原因可能在于： ①武功山试验点选择了人为干扰和旅游开发强度大的区域，游人踩踏行为较多，致使土壤致密性增加，降低了土壤孔隙度，土壤容重也会随之增大，进而影响土壤入渗性能；而衡山的试验点选择在人为干扰较少且自然状态下较为平坦的区域作为试验点，且为了保持下垫面一致，试验开始前清理了地表的覆盖物，铲平了突出的土堆和石块以及一部分杂草，从而减少了人为外界干扰的影响和坡度的影响； ②武功山试验点选择在海拔1 600 m以上山地草甸区域，土壤类型为亚热带山地草甸土壤，而衡山试验点选择在1 300 m以下的山地林地区域，土壤为亚热带山地红黄壤，两种土壤物理性质差异较大。其中武功山高海拔草甸地区在降雨作用下，表层土壤极易侵蚀，造成土壤质地变化和结构改变，影响了土壤入渗性能。衡山试验点则处于森林区域，根据高冠民[47]等人的研究表明衡山土壤较为深厚，成土母质以花岗岩为主，有机质含量随海拔上升有一定增加的趋势，其原因在于随海拔上升温度降低，微生物活性减弱，减少了对有机质的消耗，促进了有机质的积累。土壤中存在较多的植物根系，表明各类植物丰富，植被覆盖率高，土壤侵蚀较少。质地主要为壤土，土壤结构为团粒结构，通气透水性良好。这是由于在植物生长过程中地下根系在土体中交错、穿插，既能固持土壤，同时也对岩石有破碎作用，使得土壤土质较为疏松，显著改善了土壤质地和结构等理化参数，还有可能产生土壤优先流现象进而影响土壤入渗性能。

在衡山的入渗试验中主要考虑了土壤物理性质指标的影响，其中有机质含量与土壤黏粒含量促进了水稳性团聚体的形成，而水稳性团聚体的形成有效改善了土壤结构，使土壤具有良好的通气透水性能，进而影响土壤水分入渗。但是在前人研究中指出影响入渗性能的因素众多，有研究表明稳定入渗率与速效钾等土壤速效养分含量[44]、坡位和坡向[47]具有相关性。因此要全面探索土壤入渗性能影响因素仍需更加深入的研究。

4 结 论

(1) 衡山上测定各试验点的土壤入渗率性能和入渗过程呈现一定的规律，入渗性能的大小特征表现为稳定入渗率随海拔上升逐渐增大，入渗过程特征表现为初始入渗率很大，随着入渗过程的推进，入渗率迅速减小，最终达到稳定入渗，前10 min入渗呈快速减小的趋势，在10～30 min呈现缓慢减小的趋势，30 min以后入渗率趋于稳定状态，证明了点源入渗法能在短时间内准确测量比较完整入渗速率变化过程，比其他测量方法更快捷方便。

(2) 土壤水分入渗过程十分复杂，且土壤容重、土壤质地、有机质等因素之间还存在相互作用，在相关性分析中，既验证了稳定入渗率随海拔增加而增大的特征，还表明了稳定入渗率与>0.25 mm水稳性团聚体呈极显著正相关关系；与土壤容重呈负相关关系，但相关性并不显著。而有机质、土壤质地通过影响水稳性团聚体的形成，间接对土壤入渗性能产生影响。

(3) 通过拟合结果可以看出各入渗模型拟合结果相关系数均大于0.95，都能较好地对衡山各试验点入渗速率进行拟合计算。其中Philip模型由于参数A表征的稳定入渗率均为负数，使其物理意义不明确，表明Philip模型在衡山土壤入渗率拟合中有一定的局限性；Horton模型能较好地反映衡山土壤入渗性能随海拔变化的特征，即山顶>山腰>山麓，稳定入渗率随海拔增加而增大；Kostiakov模型能反映各试验点的入渗率衰减特征，即山麓>山顶>山腰；而就R2而言，Kostiakov模型拟合结果相关系数高达0.995大于Horton模型公式(0.992)，所以认为Kostiakov模型的拟合精度要优于Horton模型，说明Kostiakov模型公式更加适用于描述衡山土壤水分入渗特征，也同时说明点源入渗法在测量山地入渗中是可行的。