三构态驱动变胞并联球铰设计与分析

胡旭宇 刘宏昭

(西安理工大学机械与精密仪器工程学院， 西安 710048)

0 引言

变胞并联机构由于具有随任务变化而变自由度、变拓扑结构的特点和高承载能力、高精度等优点，已成为机构学与机器人学领域的研究热点之一。KONG等[1]通过可锁运动副，提出一种新型三维平移和三维转动2模式变胞并联机构。TIAN等[2]通过开启与锁死杆件，基于变胞连杆，综合出一类3R、1T2R、2T1R和3T 4模式变胞并联机构。王冰等[3]基于具有解耦特性的变胞球面五杆机构，通过串联一个四自由度支链综合出变胞支链，应用3条相同的变胞混联支链构造了一类变胞并联机构。GAN等[4-5]提出了一种变胞虎克铰Uv，并分析了3-UvCUv变胞并联机构的几何约束。YE等[6-7]基于一种三构态的平面五杆变胞机构，通过构建混联支链，综合出含约束奇异特性的变胞并联机构。ZHANG等[8]基于Bennett闭链构建混联支链，提出一种新型变胞并联机构。于红英等[9]通过锁住不同运动副的方式实现变胞支链的构态变换，提出一种基于基本支链构型的变胞并联机构设计方法，并应用所提出的综合方法，综合了动平台为Bricard机构的变胞并联机构。刘伟等[10]提出了一类2模式可转换变胞并联机构。文献[11-12]中通过将3个交于一点的转动副替换球铰，提出了一种关节锁死的变胞球铰Sv。

综上可见，学者们通过研究机构的支链奇异特性实现变胞。一些机构需要在远离机架的关节上安装伺服电动机或关节锁死装置，影响机构的动态性能，并使机械结构变得复杂。通过驱动副的开启与锁死可有效避免变胞过程中的约束奇异以及支链奇异，而现有文献中关于驱动变胞并联机构的研究较少，特别是缺乏关于系统的包含一维、二维和三维转动的驱动变胞并联球铰的相关研究。

本文基于有限旋量法提出一种可以实现一维转动、二维转动和三维转动的三构态驱动变胞并联球铰。根据螺旋理论分析机构各构态的自由度，利用矢量法和几何约束关系分析机构全构态运动学。最后基于驱动变胞并联球铰，提出一种八模式3-SPS/SmPU变胞并联机构。

1 3-RRR并联机构型综合

3R球面并联机构动平台的有限旋量集合可表示为

{sf,PM}={sf,cΔsf,bΔsf,a}

(1)

其中

式中 {sf,PM}——动平台的有限旋量[13]集合

{sf,c}——转动副Rc的有限旋量集

θc——转动副Rc从1位置绕其轴线sc转到2位置所转过的角度(图1)

ro——转动副Rc的矢径

图1 刚体有限转动示意图Fig.1 Sketch of rigid body finite rotation

串联支链RbRc表示为

(2)

而有限旋量三角积[14-15]表示为

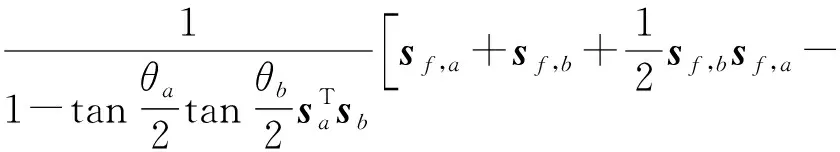
(3)

式中O——零向量

由于动平台与所综合的三自由度支链自由度相同，因此不需要在描述动平台的有限旋量因式末端添加线性无关的转动和移动因子。三自由度支链{sf，iL}的标准型为

(4)

式中 {sf，iL}——轴线交于o点的3个转动副(Ra、Rb、Rc)的串联支链集合

由于支链标准型中的3个转动副完全相同，故支链RaRbRc无需进行运动副位置互换。可以通过运动副的替换综合三自由度支链标准型对应的所有可行衍生支链。

根据旋量三角积的运算法则可得

{sf,iL}={sf,iL}S

(5)

(6)

式中 {sf,iL}S——球铰S的有限旋量集

{sf,iL}U——虎克铰U的有限旋量集

{sf,iL}R——转动副R的有限旋量集

综上可得所有可行三自由度支链，如表1所示。

表1 三自由度支链Tab.1 Three degrees of freedom branches chain

任取表1中3条支链，根据3条支链的等效转动副交点共点即可综合得到3R球面并联机构。如3条RaRbRc支链中9个转动副轴线交于一点。如图2所示，为避免杆件间的碰撞干涉设计成圆弧形杆，为使计算简单方便将每条支链的转动副轴线初始位置分布为两两垂直，且3个驱动副轴线两两垂直。

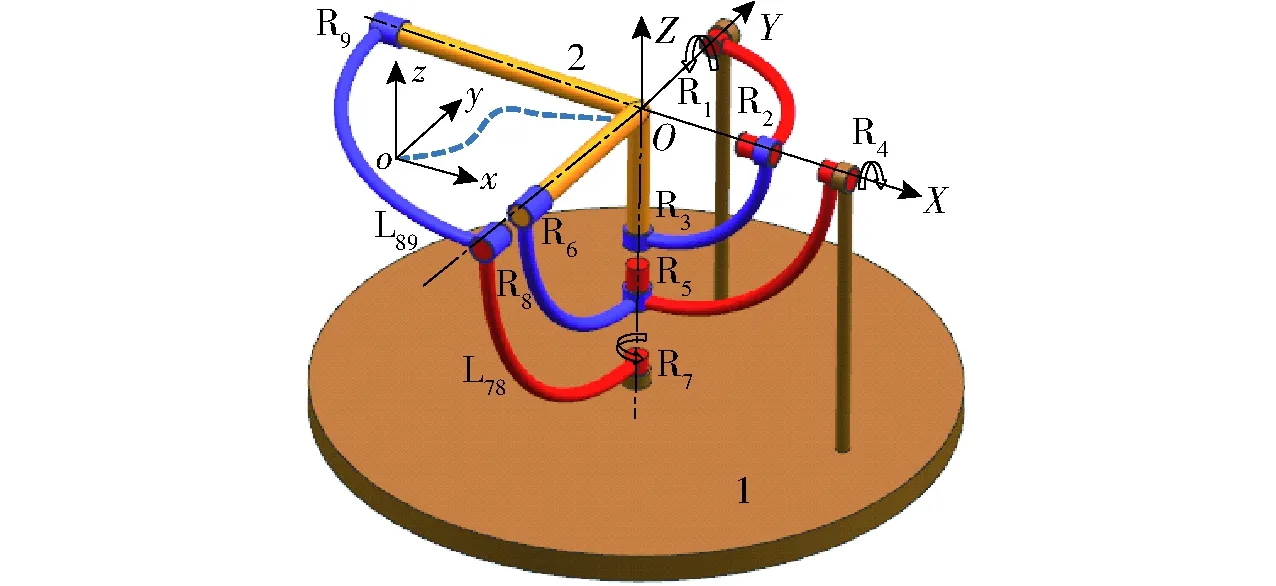
图2 3-RRR变胞并联机构Fig.2 3-RRR metamorphic parallel mechanism

2 变胞并联机构的结构特性

如图2所示，3-RRR变胞并联机构由定平台1、动平台2以及3条相同的支链构成，每条支链由3个转动轴线两两垂直的转动副和圆弧形杆构成(支链1由R1、L12、R2、L23和R3构成，支链2由R4、L45、R5、L56和R6构成，支链3由R7、L78、R8、L89和R9构成)。3-RRR变胞并联机构具有3种转动构态：只驱动R1、只驱动R4或只驱动R7的3种运动模式，定义为构态1；同时驱动R1和R4、同时驱动R1和R7或同时驱动R4和R7的3种运动模式，定义为构态2；同时驱动R1、R4和R7，定义为构态3，包含1种运动模式。

3 机构自由度分析

由于3-RRR变胞机构构态1和构态2下的3种运动模式情况相似，故每种构态只分析其中一种。

3.1 构态1机构自由度分析

如图2所示，以动平台中心为原点，以R1的转动轴线为Y轴，R4的转动轴线为X轴，建立定坐标系OXYZ(固接于定平台)。在构态1下，设驱动副R4和R7锁定，只驱动R1，变胞并联机构等效为2-RR/RRR，计算2-RR/RRR并联机构各支链在定坐标系下的运动螺旋

(7)

式中，设(ai,bi,ci)和(di,ei,fi)(i=1，2，3)分别表示R2、R5、R8和R3、R6、R9的几何中心Aj(j=2，5，8，3，6，9)在固定坐标系的位置。根据运动螺旋与其约束螺旋互易求各支链的约束螺旋

(8)

自由度计算公式为[16-17]

(9)

其中

d=6-λv=k-t

式中M——机构自由度d——机构阶数

λ——公共约束数

n——包括机架的构件数目

g——运动副数目

fi——第i个运动副自由度

v——多环并联机构在去除公共约束的因素后的冗余约束数目

t——多环并联机构所有支链的反螺旋去除公共约束后的反螺旋数目

k——多环并联机构所有支链的反螺旋去除公共约束后的反螺旋系最大无关组数

ξ——机构中存在的局部自由度

根据构态1的约束螺旋式(8)，可得公共约束数λ=3，则机构阶数d=3，并联机构所有支链的反螺旋去除公共约束后的反螺旋数目t=2，并联机构所有支链的反螺旋去除公共约束后的反螺旋系的最大无关组k=2，多环并联机构在去除公共约束的因素后的冗余约束的数目v=0，不是冗余机构。根据式(9)，2-RR/RRR并联机构的自由度为

M=3(6-7-1)+7+0-0=1

(10)

由此可知，只驱动R1时，此变胞并联机构具有1个绕y轴转动的自由度。

3.2 构态2机构自由度分析

此构态下，锁定1个驱动，不妨设R7锁定，当3-RRR变胞并联机构只驱动R1和R4时，其支链1和支链3的运动螺旋及其反螺旋分别为式(7)中第1式、第3式和式(8)的第1式、第3式，计算2-RRR/RR并联机构的支链2在定坐标系下的运动螺旋

(11)

根据运动螺旋与其约束螺旋互易求支链2的约束螺旋

(12)

根据式(8)的第1式、第3式、式(12)和自由度计算式(9)，可得此构态下的自由度为

M=3(7-8-1)+8+0-0=2

(13)

由此可知，当驱动R1和R4时，此变胞并联机构具有绕x轴和y轴转动的自由度。

3.3 构态3机构自由度分析

同时驱动R1、R4和R7，其支链1的运动螺旋及其反螺旋分别为式(7)中第1式和式(8)的第1式，支链2的运动螺旋及其反螺旋分别为式(11)和式(12)。计算3-RRR并联机构支链3在定坐标系下的运动螺旋

(14)

根据各运动螺旋与其约束螺旋互易求得支链3的约束螺旋

(15)

根据式(8)的第1式、式(12)、式(15)和自由度计算式(9)，可得此构态下的自由度为

M=3(8-9-1)+9+0-0=3

(16)

由此可知，此构态下3-RRR并联机构具有绕x、y和z轴转动的自由度。

同样可以得到，构态1中只驱动R4(或R7)运动模式下的自由度和构态2中同时驱动R4和R7(或R1和R7)时的自由度。通过对3种构态下自由度的计算可知，3-RRR变胞并联机构具有3种转动构态，各构态下的自由度如表2所示。

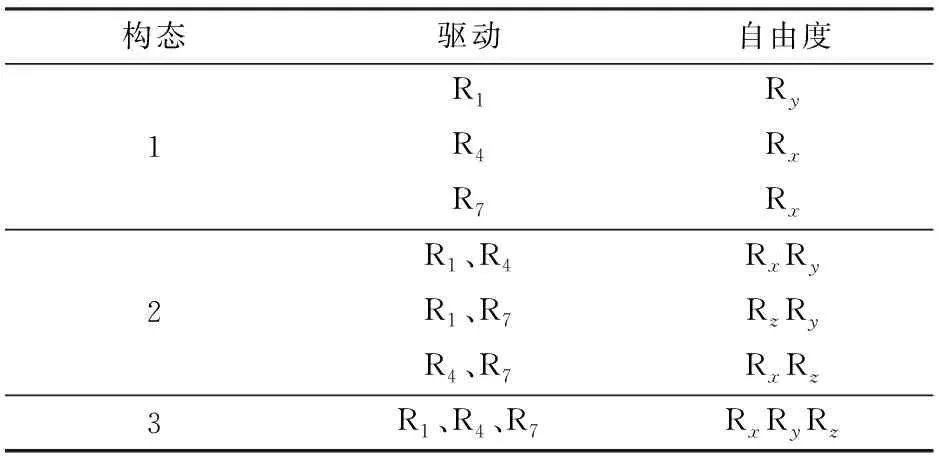
表2 驱动变胞并联球铰的运动模式Tab.2 Motion mode of actuated metamorphic parallel spherical joint

由于3-RRR机构具有一维、二维和三维3种转动构态，其三维转动构态与球铰等效，且通过驱动的锁死与开启实现机构的变胞，故可称作三构态驱动变胞球铰。

4 运动学分析

如图2所示，以动平台中心为原点，以R1的转动轴线为y轴，R4的转动轴线为x轴，在动平台上建立动坐标系oxyz(初始状态时，动坐标系与定坐标系重合)。

4.1 变胞并联机构运动学分析

已知动平台的姿态角(设动平台绕动坐标系x、y和z轴转动角分别为α、β和γ)和3-RRR变胞并联机构的各杆件长度，求驱动副R1、R4和R7转动角(分别设为θ1、θ2和θ3)。机构动平台坐标旋转矩阵R采用Y-X-Z型欧拉角，可得

R(βY,αX,γZ)=[RYβ][RXα][RZγ]

(17)

与动平台相连的转动副R3、R6和R9的各中心点在动坐标系的坐标矢量Aj为

(18)

与动平台相连的转动副R3、R6和R9的各中心点在定坐标系的坐标为

(19)

根据定长杆L23、L56和L89为转动副R3、R6和R9中心坐标与中间转动副R2、R5和R8中心坐标之差，可得

(20)

根据式(20)，可得3-RRR变胞并联机构的运动学逆解

(21)

对式(21)两边求导，可得构态3机构雅可比矩阵为

(22)

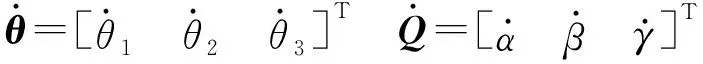
式中J——机构雅可比矩阵

同理可求得驱动变胞并联球铰构态1和构态2下机构的运动学逆解。

4.2 变胞并联机构运动仿真

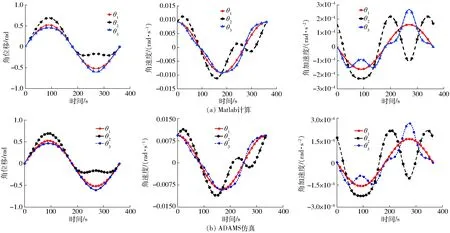
图3 3-RRR并联机构运动曲线Fig.3 Motion curves of 3-RRR parallel mechanism

从图3可以看出，运动学模型的计算结果与ADAMS仿真结果一致，验证了所建运动学模型的正确性[18-20]。同样的方法可验证构态1和构态2下机构的运动学。对三构态驱动变胞并联球铰运动学的分析为机构的实际工业应用奠定了一定的理论基础。且由于运动学是研究机构的输与入输出之间的映射关系，故同时也验证了驱动变胞并联球铰运动的可行性。

5 应用

基于3-RRR驱动变胞并联球铰，通过在动平台上串联P副和U副，构成SmPU驱动变胞支链。由于驱动Sm后驱动变胞支链的自由度为3，结合驱动选取原则，通过与3条包含3个驱动副的六自由度支链组合，提出了一种多模式3-SPS/SmPU驱动变胞并联机构。初始状态下，3-SPS/SmPU变胞并联机构中U副转动轴线分别平行于定坐标系的y轴和x轴。

图4 3-SPS/SmPU变胞并联机构Fig.4 3-SPS/SmPU metamorphic parallel mechanism

如图4所示，图中带箭头的运动副表示驱动副。当变胞球铰无驱动，3-SPS/SmPU变胞并联机构具有绕y轴和x轴转动和沿z轴移动的3个自由度；当变胞球铰处于构态1：只具有绕y(或x)轴转动时，3-SPS/SmPU变胞并联机构具有绕y轴和x轴转动和沿z轴和x(或y)轴移动的4个自由度；变胞球铰只具有绕z轴转动时，3-SPS/SmPU变胞并联机构具有绕y轴、x轴和z轴转动和沿z轴移动的4个自由度；当变胞球铰处于构态2：具有绕y轴和x轴转动时，3-SPS/SmPU变胞并联机构具有绕y轴和x轴转动和沿z、x、y轴移动的5个自由度；变胞球铰具有绕z轴和x(或y)轴转动时，3-SPS/SmPU变胞并联机构具有绕x、y、z轴转动和沿z轴和y(或x)轴移动的5个自由度；当变胞球铰处于构态3(即具有三维转动自由度)时，3-SPS/SmPU变胞并联机构具有6个自由度。即3-SPS/SmPU变胞并联机构具有8种运动模式。

6 结论

(1)提出了一种驱动位于定平台的3-RRR驱动变胞并联球铰，通过便捷的开启与锁死驱动即可实现机构的变胞。

(2)建立了3-RRR驱动变胞并联球铰的运动学模型，其与ADAMS仿真结果一致，验证了所建运动学模型的正确性。

(3)基于3-RRR变胞并联球铰，通过串联P副和U副，构成SmPU变胞支链。并将变胞支链SmPU应用于八模式3-SPS/SmPU变胞并联机构。