基于改进人工势场法的路径规划决策一体化算法研究
2019-10-10袁朝春翁烁丰何友国SHENJie
袁朝春 翁烁丰 何友国 SHEN Jie 陈 龙 王 桐
(1.江苏大学汽车工程研究院, 镇江 212013; 2.密歇根大学迪尔本分校, 迪尔本 MI 48128)
0 引言
路径规划决策算法是无人驾驶汽车的重要理论依据之一[1-3]。车辆行驶环境复杂而多变,这对无人驾驶汽车的路径规划决策提出了很高的实时性要求。目前常用的路径规划算法包括人工势场法、网格法、可视图空间法等。人工势场法采用虚拟的斥力与引力建立梯度力场,根据梯度力场矢量方向对车辆路径进行规划,该算法规划的曲线平滑,计算量较小,但易陷入局部最优点[4];网格法通过将当前环境划分为系列网格,并通过该网格是否存在障碍物判断网格的可通行性,以此规划出一条可通行路线,网格法需要大量的计算量,限制了算法的实时性[5];可视图空间法将环境中障碍物抽象为多边形,并绘制起点与终点之间的多条连线,并在此基础上筛选最优路径,该方法灵活性较差,在复杂变化环境下表现不佳[6]。
目前研究较多的路径跟踪算法有基于驾驶员预瞄模型的路径跟踪算法和基于模型预测控制算法的路径跟踪算法。驾驶员预瞄模型根据车辆未来的预估位置与目标位置的差距进行补偿决策控制,主要分为单点与多点预瞄模型,能够获得较好的跟踪控制效果[7-8];模型预测控制算法通过设置不同的评价函数来确定路径跟踪过程中各参数量对车辆的重要程度,最终获得理想的控制结果[9]。然而,现阶段的路径跟踪算法环节需要较大的数据量与计算量,导致无人驾驶汽车的路径规划与决策控制环节存在着时滞,会引起检测信息与真实行驶环境的偏差。
本文基于车辆行驶过程中的环境信息与运动学信息对行驶碰撞风险等级进行评估,并且基于车辆动力学因素及环境交通参与者状态建立改进人工势场模型,将无人驾驶汽车的路径规划与控制决策相结合建立控制与决策一体化算法,以期为无人驾驶汽车在复杂环境下的实时控制提供帮助。
1 车辆行驶环境安全性判定
车辆行驶环境动态复杂而多变。为了保证行驶过程中的安全性,本文基于车辆行驶运动学特性与车辆行驶环境特征,建立车辆横、纵向安全模型,以综合反映车辆行驶过程中的安全性。
1.1 纵向安全模型
为了反映车辆在行驶过程中的纵向安全特性,本文建立了一种基于道路、车辆特征的分级安全距离模型,以体现车辆与环境交通参与者的不同级别的碰撞风险,为车辆纵向速度的控制决策提供合理依据。
(1)直行工况
行驶过程中,车辆的实际制动能力受车辆性能参数、轮胎-路面摩擦因数和实际驾驶环境等的影响,假设车辆制动系统可以发挥道路的最大制动效能,则最大制动减速度主要受轮胎-路面摩擦因数和实际驾驶环境的影响。车辆行驶过程中,纵向方向上需保持的距离如图1所示。

图1 车辆纵向安全距离Fig.1 Longitudinal safety distance model
结合车辆运动学特征并综合道路环境、车辆因素影响,利用车辆最大制动减速度、自车车速、前车车速、前车减速度等信息建立纵向分级安全距离模型[10-12],为
(1)
(2)
式中Dbr1、Dbr2——1、2级安全距离阈值,m
vx——车辆当前行驶纵向速度,m/s
ar-max——车辆最大制动减速度,m/s2
vlf——当前车道前方交通参与者速度,m/s
alf——当前车道前方交通参与者加速度,m/s2
Tbr——自车制动响应时间,s
(2)弯道工况
如图2所示,弯道行驶过程中,车辆的实际行驶路径的距离与传感器检测的直线距离有所偏差。
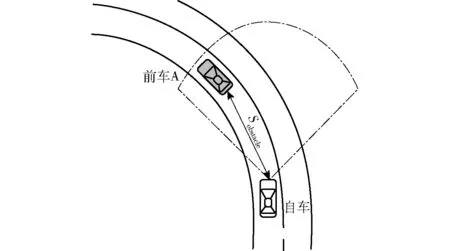
图2 弯道行驶工况示意图Fig.2 Vehicle driving on a bend
传感器的测量结果Sobstacle与车辆的预期行驶轨迹存在偏差,无法准确地描述自车行驶到前车位置过程中实际行驶的距离。为了保证安全判断的准确性,本文按照图3所示的方法对交通参与者与自车之间的距离作了修正计算。
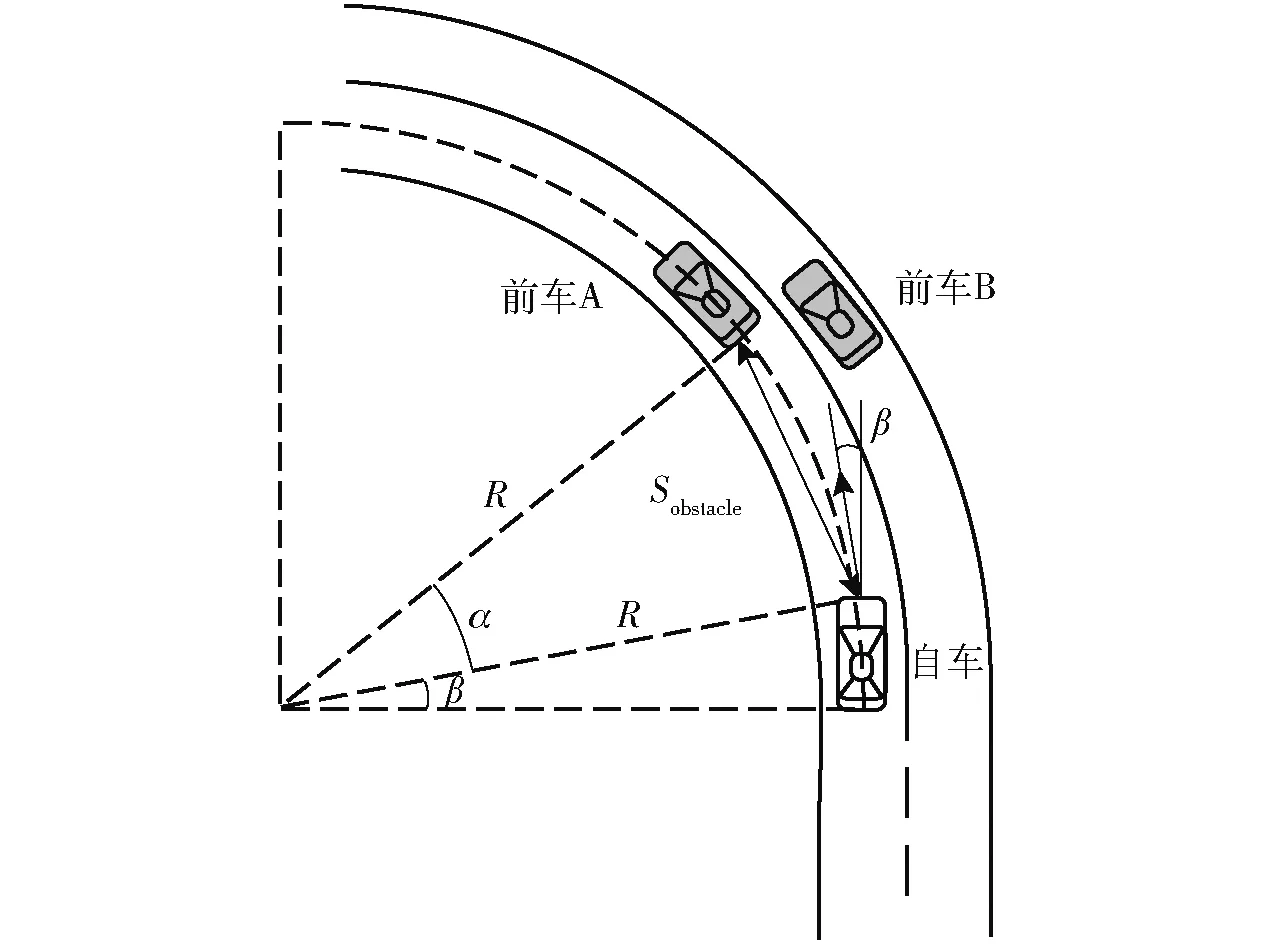
图3 车辆在弯道行驶工况中的修正距离Fig.3 Corrected distance on a bend
自车与前方交通参与者之间的修正距离为
(3)
式中S′obstacle——修正后自车与前方交通参与者距离,m
α——车辆行驶轨迹扇形的圆心角,(°)
δ——前轮转角,(°)
l——前后轴距之和,m
R——车辆转向半径,m
根据前方交通参与者修正距离与分级安全距离模型分级阈值的关系,得到车辆目前行驶环境纵向安全级别为
(4)
1.2 横向换道安全模型
车辆行驶过程中,不仅需要合理控制纵向速度以保证车辆不会与前方交通参与者发生碰撞,还需要在当前车道存在拥堵或静止障碍物时控制车辆执行换道操作。为了保证换道过程中的安全性,建立了车辆横向换道安全模型[13-15]。
换道过程中,为了保证车辆不会与前方车辆发生碰撞事故,结合无人驾驶汽车与前向环境交通参与者的运动学信息,建立前向换道防碰撞模型为
(5)
式中fjud——换道过程前方交通参与者碰撞风险判别参数
Tchange——换道所需时间,s
vf——邻车道前方交通参与者车速,m/s
af——邻车道前方交通参与者加速度,m/s2
Sremain——预留安全车距,m
Ssf——车辆与邻车道前方障碍物纵向距离,m
同时,为了保证车辆不干涉相邻车道后方车辆的正常行驶,结合无人驾驶汽车与后向环境交通参与者的运动学信息,建立了后向换道防追尾模型
(6)
式中bjud——换道过程后方交通参与者碰撞风险判别参数
vb——邻车道后方交通参与者车速,m/s
ab——邻车道后方交通参与者加速度,m/s2
当满足条件:fjud>0和bjud>0时,车辆安全换道状态参数Csafe为1,不满足时,Csafe为0。
2 车辆7自由度动力学模型
为了更好地分析车辆动力学主要特征,作如下假设:直接将前轮转角作为方向盘输入,不考虑转向系统影响;不考虑车辆垂直运动;假设车辆为刚性系统,忽略悬架系统;忽略侧向风对车辆产生的影响。根据车辆特性,建立图4所示的车辆7自由度动力学模型[16-18]。
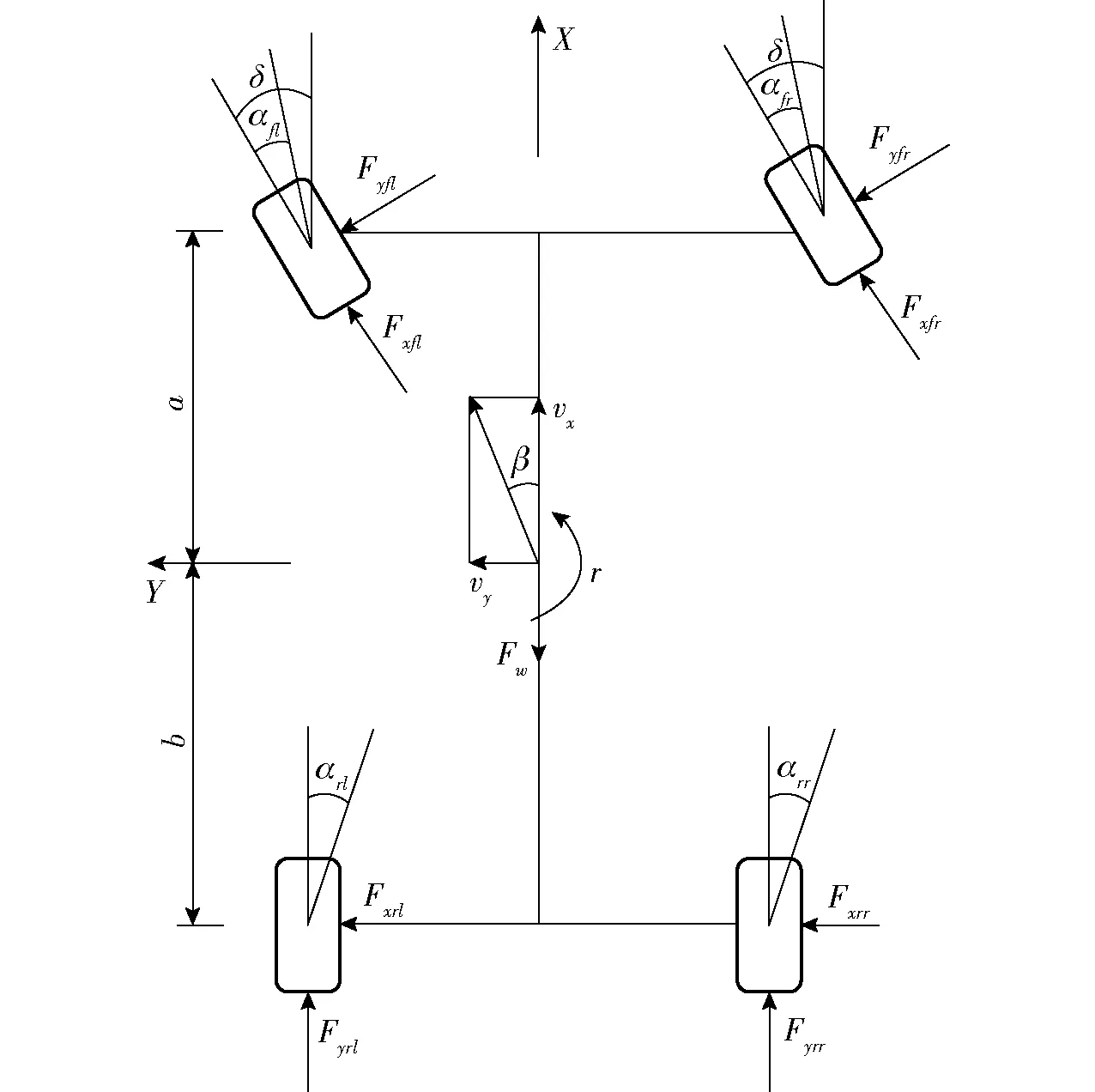
图4 7自由度车辆动力学受力示意图Fig.4 Forces of seven degrees of freedom model
(1)动力学方程
7自由度车辆动力学模型包括2个平动(纵向、侧向运动)和5个转动(横摆运动、4个车轮转动),动力学方程为
(7)
式中vy——横向车速,m/s
r——横摆角速度,rad/s
Fxi、Fyi、Fzi——轮胎纵向力、侧向力、垂向力,i分别对应左前轮fl、右前轮fr、左后轮rl、右后轮rr,N
m——整车质量,kg
a、b——前后轴到质心的距离,m
Iz——整车绕Z轴的转动惯量,kg·m2
tw1——前轴轮距,m
tw2——后轴轮距,m
Fw——车辆行驶过程中空气阻力
(2)约束方程建立
采用魔术公式建立轮胎模型,考虑到车辆在行驶过程中由于加速或减速引起各车轮的垂直载荷偏移,建立各轮胎垂向载荷力求解公式为
(8)
式中hg——整车质心高度,m
各轮胎侧偏角计算公式为
(9)
各车轮轮心在车轮坐标系下纵向速度为
(10)
式中vt_fl、vt_fr、vt_rl、vt_rr——轮胎坐标系下的轮胎纵向速度,m/s
(3)Simulink模型建立
如图5所示,使用Simulink搭建7自由度整车动力学模型。

图5 整车动力学模型Simulink框图Fig.5 Simulink block diagram of vehicle dynamics model
3 路径规划决策一体化模型
局部路径规划算法的核心是在全局路径规划算法的基础上寻找2个节点之间的行驶最优路径[19]。现有算法需要先根据环境情况规划一条行驶路线,通过控制器控制车辆在此路径上进行跟踪。然而,智能车辆行驶过程中,环境信息与车辆自身信息处于不断的更新状态,传统路径规划决策算法在规划层与决策层的脱离可能引起无人车控制的不稳定性。
在传统路径规划与路径跟踪的基础上,利用多类约束下的虚拟斥力与引力模型体现智能车在交通法规、交通事故风险、车辆动力学等方面所受的约束。用路径规划决策一体化模型代替传统路径规划算法与路径跟踪控制器,为车辆提供合理的局部路径的同时提供当前所需的执行机构的最优控制值,为复杂工况的智能车辆主动避撞规划提供更加合理高效的方法。算法流程如图6所示。

图6 改进人工势场算法流程示意图Fig.6 Flow chart of improved artificial potential field algorithm
3.1 人工引力建模
人工虚拟引力代表智能车辆行驶过程中对其具有吸引作用的环境因素,主要有全局规划虚拟引力与车辆换道虚拟引力,分别用于提供智能车辆行驶过程中克服环境阻力正常行驶所需的牵引力及换道操作对车辆的牵引作用。
3.1.1全局规划虚拟引力建模
全局规划路线虚拟引力用于提供车辆正常行驶所需的牵引力,其大小与当前行驶道路的最高限速、车辆在该路面行驶的滚动阻力系数以及车辆自身质量有关。该设计虚拟引力是为保证智能车辆在无交通参与者或交通参与者碰撞威胁级别为0级的道路上能够在该虚拟引力的作用下持续加速,并在车辆速度与当前道路限速相同为止之后达到受力平衡状态并保持匀速行驶,直到前方出现交通参与者或道路限速发生变化为止。而在前方道路有其他交通参与者时,车辆将根据该交通参与者对自车的威胁级别进行处理,当威胁级别处于1级时,全局规划引力将仅提供保持车辆在当前速度下正常行驶的力,当威胁级别处于0级时,全局规划虚拟引力为0,释放车辆油门。
在无坡道的道路上,该虚拟引力表示为

(11)
式中μroll——车辆滚动阻力系数
A——车辆的等效迎风面积,m2
Cw——车辆的风阻系数
vlimit——车辆行驶最高速度,m/s
Kattract-plan——全局规划虚拟引力系数
3.1.2智能车辆换道引力建模
智能车辆行驶过程中,当遇到存在前方交通参与者或其他阻碍车辆正常行驶的状态时,车辆需要进行换道行驶。该引力为智能车辆的换道提供决策与执行依据。
车辆换道引力受当前行驶路面的滑动摩擦因数、车辆行驶速度、车辆已完成的换道距离、车辆质量等因素决定。车辆换道引力计算式为
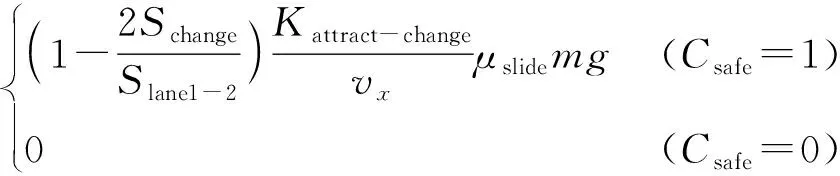
(12)
式中Schange——车辆已完成的横向位移距离,m
Slane1-2——车辆与所在车道及换行车道的中线距离,m
μslide——路面滑动摩擦因数
3.2 人工斥力建模
虚拟斥力代表车辆行驶过程中对车辆行驶具有排斥作用的环境因素,用于引导车辆规避交通参与者(车辆、行人、道路两侧灌木等)与车辆自身特性约束(动力学特性、运动学特性)。主要分为:前向交通参与者斥力与前方传感器检测盲区虚拟斥力。
3.2.1前向交通参与者斥力建模
前向交通参与者斥力用于表征前方交通参与者对于车辆产生的影响,能充分反映前方交通参与者对于自车的威胁,可以保证车辆在发生碰撞之前完成制动或减速。
该斥力与车辆当前行驶速度、车辆与前方交通参与者理论安全距离、当前路面附着力系数、整车质量、前方交通参与者运动速度有关。以建立的交通参与者筛选算法与车辆安全距离模型作为依据,对车辆运动学特性进行合理分析,建立前方交通参与者斥力模型为

(13)
式中Kr-obstacle——前向斥力系数
μroad——当前路面最大附着力系数
Srem——行驶过程中车辆与前方交通参与者预留安全距离,m
3.2.2前方传感器检测盲区斥力建模
传感器检测盲区斥力用于反映车辆在前方存在传感器检测盲区时的制动减速度特性。该模型根据传感器检测的盲区边界,在该边界的基础上控制车辆进行制动减速,以保证车辆在该力的作用下能够避免盲区内突然出现交通参与者引起制动距离不足而导致的交通事故。
该虚拟斥力主要由前方传感器盲区边界与自车距离、自车行驶速度、当前道路附着力系数确定,计算式为
(14)
式中Kr-blind——前方传感器检测盲区斥力系数
Sblind——盲区边界与车辆当前距离,m
4 Carsim/Simulink联合仿真分析
为了验证提出模型的有效性与优越性,使用Carsim/Simulink建立了多个仿真工况,对算法有效性与时滞性进行了分析。
4.1 算法有效性验证
仿真设车辆迎风面积为1.6 m2,风阻系数为0.3,质量为1 100 kg,车辆滚动系数为0.014,道路附着力系数设为0.85,方向盘与前轮转角传动系数为20。
4.1.1全局规划虚拟引力模型验证
为了验证该模型的有效性,设置了不同的道路限速工况。工况1,车辆以初速度40 km/h在直线车道上行驶,将道路速度分别限制为60、80 km/h。车辆速度与加速度变化曲线如图7所示。
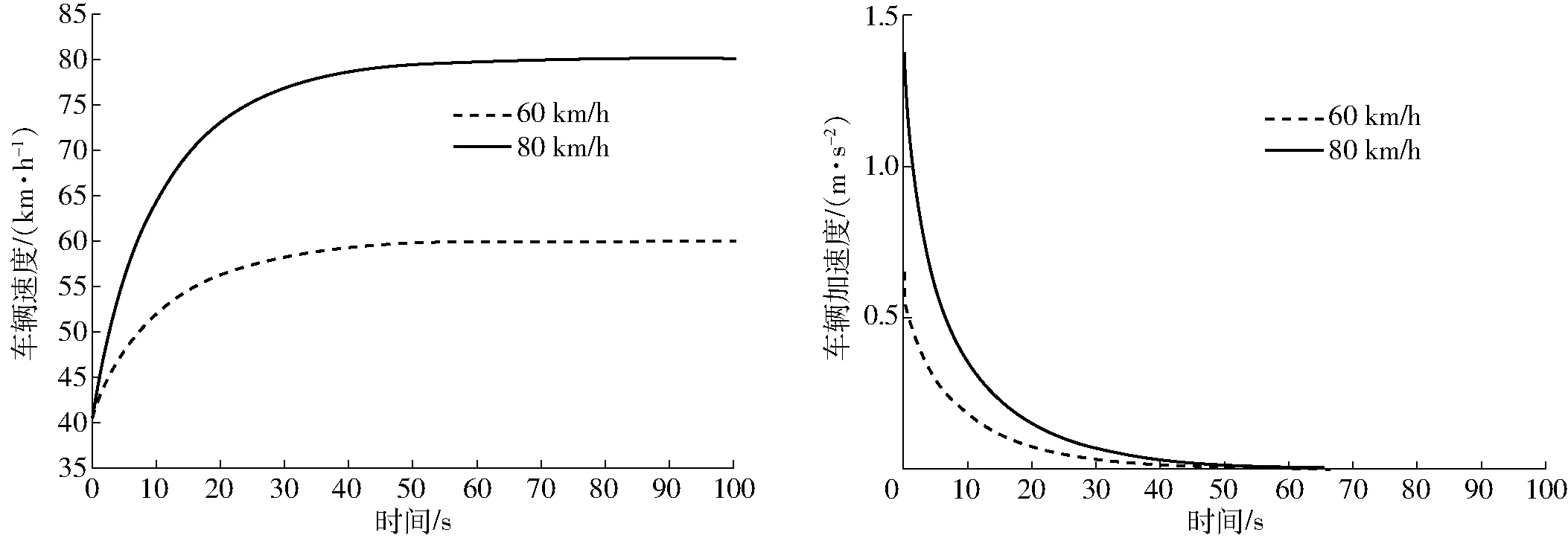
图7 车辆速度与加速度变化曲线(工况1)Fig.7 Diagram of vehicle speed and acceleration (condition 1)
由图7可以看出,在全局规划虚拟引力的作用之下,车辆在无交通参与者道路上行驶时将保持一个逐渐减少的加速度进行持续加速,并在车辆速度达到当前限速值之后保持匀速直线行驶。
工况2,车辆在直线车道上行驶,道路前1 km的限速为60 km/h,后续道路限速为80 km/h。车辆的速度与加速度变化曲线如图8所示。
由图8可以看出,在全局规划虚拟引力的作用下,前半段道路上,车辆将持续加速行驶,向60 km/h的速度持续逼近,并在道路限速改变之后改变加速度,控制车速向80 km/h的速度逼近。
工况3,车辆在直线车道上行驶,道路前1 km的限速为80 km/h,后续道路限速为60 km/h。车辆的速度与加速度变化曲线如图9所示。
由图9可以看出,在全局规划虚拟引力的作用下,前半段道路上,车辆将持续加速行驶,向80 km/h的速度持续逼近。道路限速改变之后,车辆的全局规划虚拟引力小于车辆当前所受的行驶阻力的,车辆将减速,车速向60 km/h的速度逼近。
通过上述3种工况的仿真,可以看出,全局规划虚拟引力可以引导车辆速度向当前路面的限速条件不断逼近,直到车辆行驶速度达到当前道路允许的最大行驶速度。
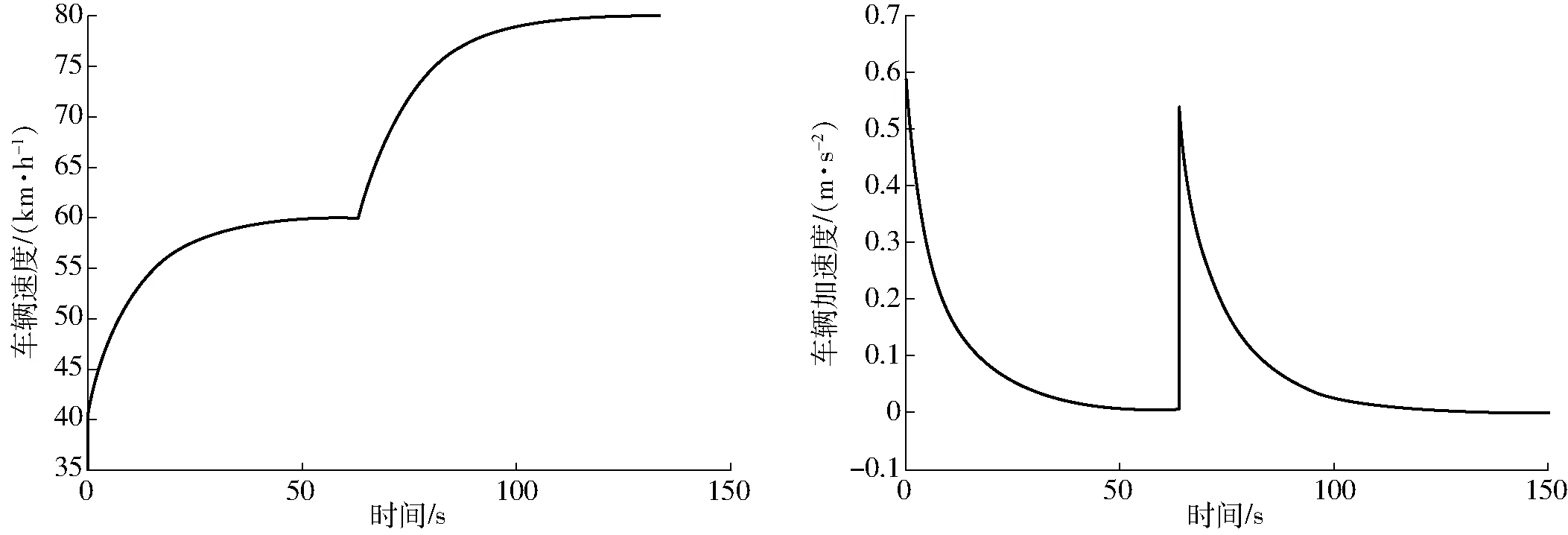
图8 车辆速度与加速度变化曲线(工况2)Fig.8 Diagram of vehicle speed and acceleration (condition 2)
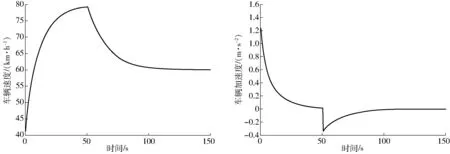
图9 车辆速度与加速度变化曲线(工况3)Fig.9 Diagram of vehicle speed and acceleration (condition 3)
4.1.2换道引力模型验证
为了验证该模型的有效性,设置了3种行驶工况,车辆分别以60、80、100 km/h的速度行驶,在换道引力与车辆行驶引力的综合作用下进行换道操作,方向盘转角变化、车辆侧向加速度变化、车辆位置变化、车辆质心侧偏角变化如图10所示。

图10 方向盘转角、车辆侧向加速度、车辆位置与车辆质心侧偏角变化曲线Fig.10 Diagram of steering angle, lateral acceleration, vehicle position and side slip angle
如图10所示,不同行驶速度下,车辆的方向盘转角峰值随车速的增加而减小;不同车速下,车辆侧向加速度的峰值均可控制在1.5 m/s2以内,可保证良好的乘坐感受;车辆位置变化为平滑曲线,转向过渡自然;车辆质心侧偏角未超过0.2°,保证了良好的车辆稳定性。
4.1.3前向交通参与者斥力模型验证
为了验证该模型的有效性,针对不同的前方交通参与者场景与自车速度进行了仿真分析。设定前方交通参与者行驶速度为20 km/h,车辆与前方交通参与者初始距离为70 m,车辆以60、80 km/h的速度沿道路行驶,车辆速度、车辆与前方交通参与者距离变化曲线如图11所示。

图11 车辆速度及车辆与前方交通参与者距离变化曲线Fig.11 Diagram of vehicle speed and distance from obstacle ahead
如图11所示,在车辆与前方交通参与者的距离小于安全距离模型所规定的阈值之后,此时,车辆前向交通参与者斥力大于道路行驶引力,车辆在合力的作用下减速,在车辆与前方交通参与者的距离大于安全距离模型所规定的阈值之后,车辆又会在道路行驶引力的作用下加速,最终,车辆与前方交通参与者的距离稳定在安全距离模型所允许的值附近。综上,车辆前向交通参与者斥力可以保证行驶中的前向碰撞安全性。
4.1.4传感器盲区斥力模型验证
为了验证该模型的有效性,设定了一种传感器盲区突然出现交通参与者的工况,该工况为:车辆以60 km/h的速度在道路上行驶,前方100 m处车辆右前方有一传感器盲区,传感器盲区于5.5 s时突然出现交通参与者,分别在未考虑传感器盲区斥力与考虑传感器盲区斥力的基础上分别进行仿真分析,车辆速度与加速度曲线如图12所示。
由图12可以看出,考虑盲区边界条件的情况下,车辆会较早地对盲区风险做出预判而提前减速,在交通参与者出现后,车辆由于预判减速的存在,留有足够的制动距离,从而规避碰撞事故的发生,而未考虑盲区的情况下,车辆在发现前方交通参与者之后才开始制动减速,制动距离过短,易导致碰撞事故的发生。
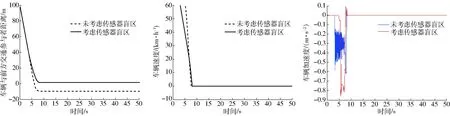
图12 车辆与盲区障碍物距离、速度、加速度变化曲线Fig.12 Diagram of vehicle distance from blind area, vehicle speed and vehicle acceleration
4.2 算法时滞分析
仿真实验所使用的运算平台CPU处理器为Intel G4560,RAM为4 GB。Matlab版本为R2014a,Carsim版本为8.1。
选用基于MPC的轨迹规划算法与基于MPC的路径跟踪算法作为参照对象,建立图13所示的联合仿真模型[20],规划量输出频率为50 Hz,设定仿真时间为5 s,使用基于Matlab中profile函数对算法进行了运行时间分析,重复进行10次,不计Carsim动力学模型耗时,得到的结果如表1所示。综合多次实验结果可知,该算法单次运行所需时间为0.06 s。
搭建图14所示的基于改进人工势场法的路径规划决策一体化算法模型,使用profile函数对其进行时滞分析。控制量输出频率为1 000 Hz,运行时间为5 s,重复10次的程序运行耗时数据如表2所示,由表2可知,单次规划决策平均运行时间为5.5×10-5s。
由表1、2可知,本文提出的路径决策规划一体化算法在时滞方面表现更优。
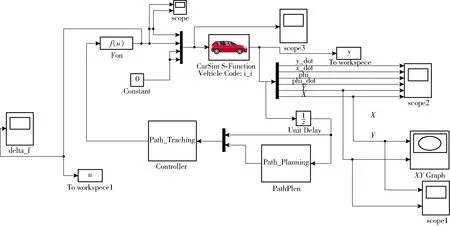
图13 基于MPC的轨迹规划算法与基于MPC的路径跟踪算法模型Fig.13 Model of MPC-based trajectory planning algorithm and MPC-based path tracking

s
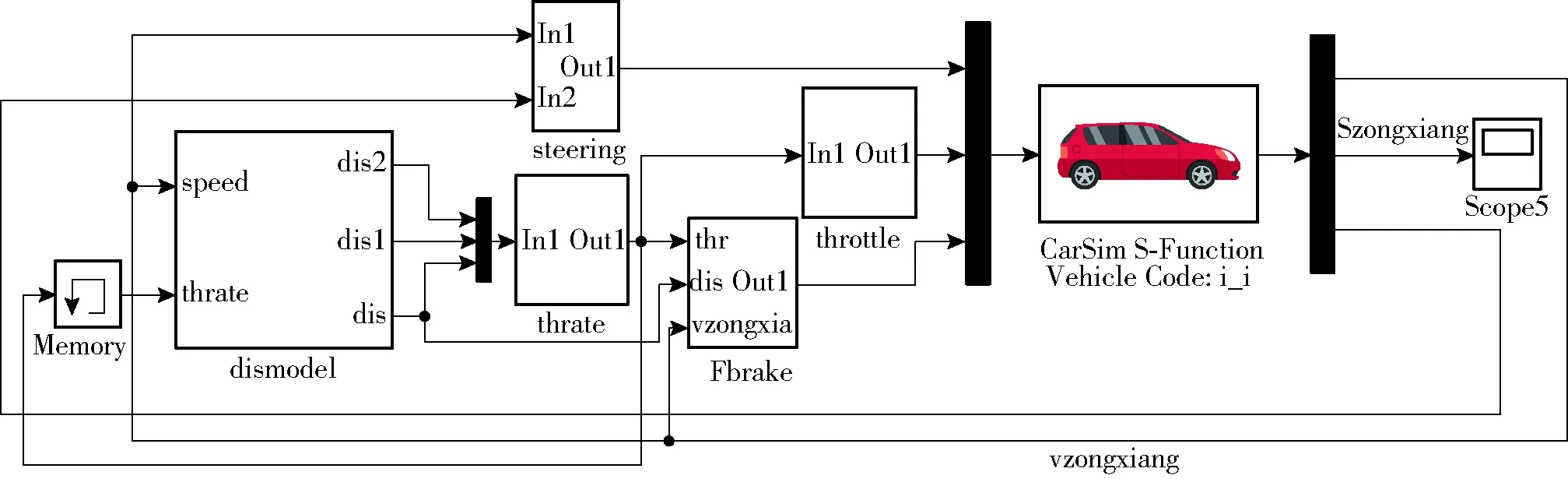
图14 基于改进人工势场法的路径规划决策一体化算法模型Fig.14 Integrated algorithm model of path planning and decision-making based on improved artificial potential field method

s
5 结论
(1)针对车辆行驶环境特征与自身运动学特征对智能车行驶过程中横纵向风险进行了分析,综合反映了智能车行驶过程中的环境安全性。
(2)针对智能车辆传感器盲区作了盲区斥力分析,避免传感器盲区带来的车辆碰撞风险。
(3)提出了路径决策规划一体化算法的概念,根据车辆与环境信息建立了改进人工势场模型,利用模型在规划车辆行驶路径的同时给出车辆控制量,减小了规划决策过程中时滞的影响。
