基于改进K均值聚类算法的燃气泄露检测研究
2019-10-08李咏豪

摘 要: 天然气管道会出现损坏现象导致天然气泄露,因此,快速准确地判断天然气的泄露具有重要意义。针对天然气泄露的检测问题,本文提出一种基于改进K均值聚类的检测方法。该方法在提取声发射信号特征的基础上,提出了基于数据点的邻点数目来选取初始聚类中心,并采用信息熵方法来确定聚类类别数目。实验结果表明,本文提出的方法较好了解决了原始K均值方法的问题,从而能准确地给出泄露检测结果。
关键词: K均值;邻点;信息熵;泄露检测
中图分类号: TH865 文献标识码: A DOI:10.3969/j.issn.1003-6970.2019.05.016
本文著录格式:李咏豪. 基于改进K均值聚类算法的燃气泄露检测研究[J]. 软件,2019,40(5):8689
【Abstract】: The damage of natural gas pipeline will lead to natural gas leakage. Therefore, it is of great significance to quickly and accurately judge the leakage of natural gas. For the detection of natural gas leakage, a detection method based on the improved K-means clustering algorithm is proposed. We select the initial cluster centers based on the number of neighbors of the data point after the extraction features of acoustic emission signal. Forthermore, we determine the number of clusters with the method of information entropy. The experimental results show that the proposed method avoids the problem brought by original K-means and achieve the better leak detection result.
【Key words】: K-means; Neighbor point; Information entropy; Leak detection
0 引言
管道運输是天然气的主要运输渠道,天然气管道现在遍布全国。由于种种原因,天然气管道会出现损坏现象导致天然气泄露[1]。因此,快速准确地判断天然气的泄露具有重要意义。当燃气发生泄露时,天然气管道的内部会将管道中的部分能量以弹性波进行释放,即所谓的声发射现象[2]。这种弹性波是一种广义的声发射信号,可以用来进行泄露判断。针对复杂的声发射信号,本文引入聚类分析方法进行燃气泄露的判断。K均值聚类方法是一种经典的无监督聚类方法[3],该方法简单方便,但也存在以下缺点,包括聚类数目K以及初始聚类中心需要预先定义,一旦定义错误就会给聚类结果带来不稳定性。本文在提取声发射信号特征的基础上,提出了改进K均值聚类方法来检测燃气信号泄露与否,并提出利用数据点的邻点数目选取初始聚类中心,以及信息熵来给出聚类数目。实验结果表明本文提出方法的具有一定的优越性。
1 改进的聚类中心选取方法
在K均值方法中,首先,用户预先输入聚类的数目K,并在数据集中随机选取K个点作为初始聚类中心,接着,计算各数据点到初始聚类中心的欧几里德距离[4],并将该数据点分配到离其距离最近的簇中,当所有数据点都分配完之后,再以各簇的均值作为新的聚类中心,重复上述过程,直到满足目标函数为止[5]。
有学者提出基于密度的初始聚类中心选取方法[6],通过计算数据点周围的数据量来选择初始的聚类中心,从而降低了K均值聚类算法随机选取初始聚类中心带来的聚类误差,提高了聚类的准确率,减少了运算次数和运算时间,但该方法只提高了初始聚类中心的准确性,仍然没有解决孤立点对后续迭代过程中聚类中心选取的影响[7],针对该问题,本文在该方法的基础上作了改进,在保证初始聚类中心选取准确的前提下消除了孤立点对聚类中心选取的影响。具体做法如下:第一步:计算每一个数据点周围的邻点数目,计算完毕后将得到的数值按从大到小排列,将数值最小的几个数据点直接删除掉,这样就可以把孤立的数据点从数据集合中删除,消除了孤立点的影响。另外,将数值最大的点作为第一个类别的聚类中心,选取距离该点最远的数据点作为第二个类别的聚类中心,以此类推,逐渐得到第三个、第四个及以后的类别聚类中心。
2 改进的聚类个数确定方法
信息熵可以量化表示一个数据集合的离散程度[8],在聚类的过程中,当数据的类别数和数据点所归属的类别发生变化时,整个数据集的信息熵之和也会发生变化。我们可以把信息熵值的变化当作是一个判定聚类类别数的判断量。由此,我们可以把相邻两个类别之间信息熵的差值变化最小看作是数据集合最稳定之时,从而可以得到数据集合最佳的聚类类别数。有学者将信息熵的概念引入到模糊聚类中,通过计算隶属度得到数据集合的信息熵[9],本文将信息熵概念引入到普通的K均值聚类算法中,利用数据点与聚类中心的距离来得到信息熵。利用前面得到的聚类中心,定义数据点到聚类中心的偏离度,根据偏离度计算聚类后的信息熵,以此来决定聚类的个数。算法的具体思想如下:
其中,Pij表示第(i)个数据点到第(j)个类中的偏离度;S表示类的信息熵;类的总体信息熵即为上式,将每一个类的信息熵求和即可得到所有类的总体信息熵。
随着聚类过程的变化,会有不同的数据点被聚类到不同的类别内,每个类别的聚类中心也在随之算法的进行不断更新,这样一来每个数据点属于各个类的偏移度会随之发生变化,从而导致了类内的信息熵变化以及整个数据集整体的信息熵变化。因此,我们做如下定义:
数据集合K均值聚类分为j个类时的状态称为数据集的第j个状态,同理,数据集第j个状态的的信息熵值为Sj。
定义数据集的信息熵跳变值如下:数据集从第j-1个状态跳跃到第j个状态的信息熵值的变化即 。
定义数据集的信息熵跃迁值[9]:数据集从第j-1个状态跳跃到第j个状态的信息熵值的变化与数据集从第j个状态跳跃到第j+1个状态的信息熵值的变化的差值:
3 实验数据采集与分析
3.1 实验数据采集
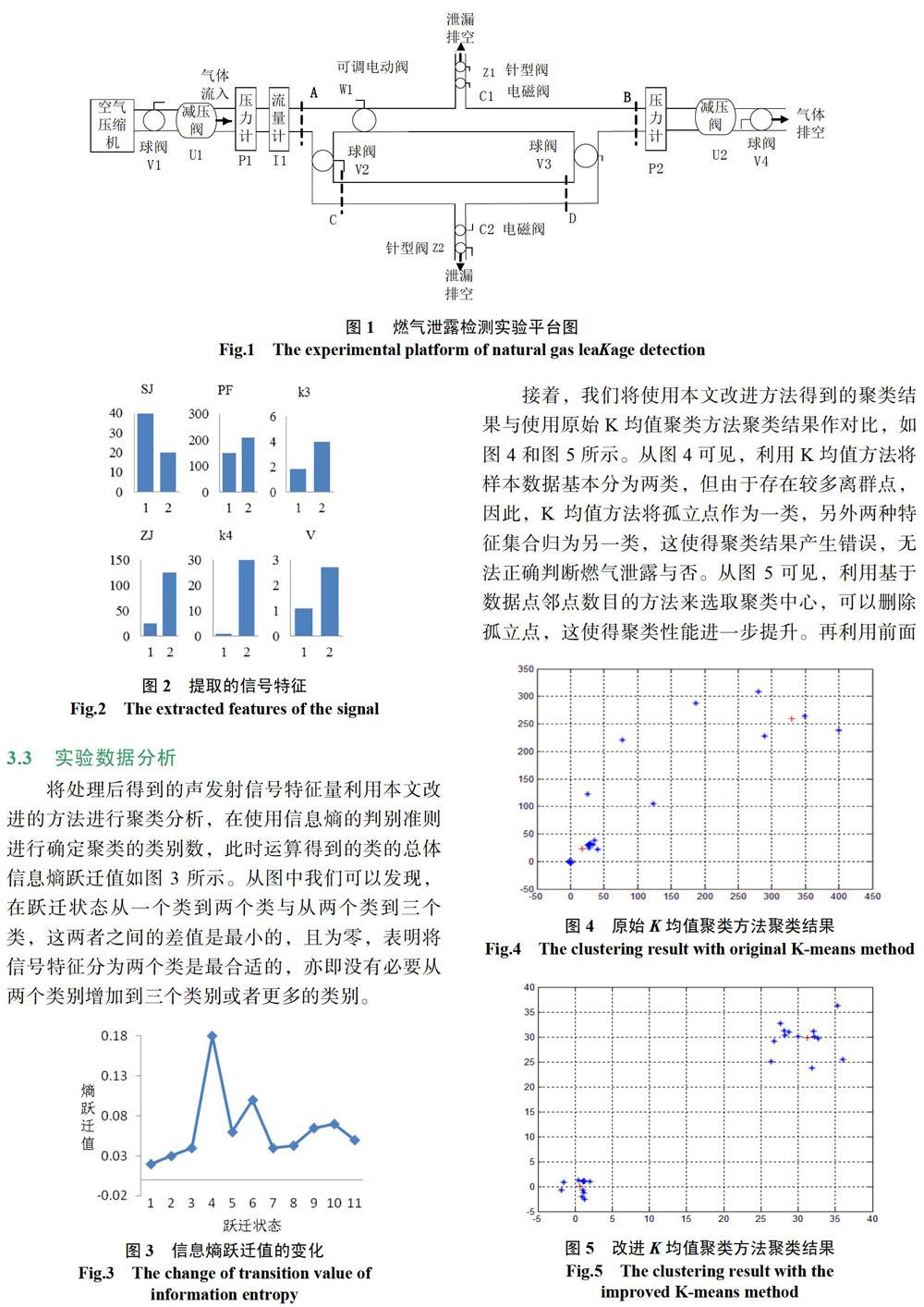
本文搭建了包括直管和支管的泄露检测平台,如图1所示。该泄露检测平台中,AB段和CD段分别为直管和支管,并且AB与CD构成一条回路,实验管径为DN20,利用空气压缩机来模拟燃气泄露,球阀V1用来控制管道的开与断,减压阀U1的作用是将高压气流变换成低压且稳定气流,压力计P1与P2用来显示气流在该位置的压力值。实验中,通过声发射传感器实时获取所有的数据。
3.2 特征提取
当管道中存在燃气泄露之后,其中传输的信号会发生一定的变化[10]。本文提取使用的特征量[10]主要有上升数目SJ,频域峰值PF,峰态k3,振铃数目ZJ,偏斜度k4,方差V。泄露信号特征与非泄露信号特征对比如图2所示,其中,柱条1和2分别表示非泄露信号和泄露信号提取的特征向量。
3.3 实验数据分析
将处理后得到的声发射信号特征量利用本文改进的方法进行聚类分析,在使用信息熵的判别准则进行确定聚类的类别数,此时运算得到的类的总体信息熵跃迁值如图3所示。从图中我们可以发现,在跃迁状态从一个类到两个类与从两个类到三个类,这两者之间的差值是最小的,且为零,表明将信号特征分为两个类是最合适的,亦即没有必要从两个类别增加到三个类别或者更多的类别。
接着,我们将使用本文改进方法得到的聚类结果与使用原始K均值聚类方法聚类结果作对比,如图4和图5所示。从图4可见,利用K均值方法将样本数据基本分为两类,但由于存在较多离群点,因此,K均值方法将孤立点作为一类,另外两种特征集合归为另一类,这使得聚类结果产生错误,无法正确判断燃气泄露与否。从图5可见,利用基于数据点邻点数目的方法来选取聚类中心,可以删除孤立点,这使得聚类性能进一步提升。再利用前面介绍的信息熵来判断聚类数目,得到对于所提取的燃气信号特征可以将其分为两类。在图5中,数据点在左下角和右上角都较为集中,左下角的数据说明,无泄露时信号各种特征都比较平稳,变化幅度不大;对于右上角的数据点,反映这些数据点的特征值的波动幅度较大。因此,根据提取到的信号的特征,我们可以判断是否存在燃气泄露。
4 结论
根据数据点的邻点数目来选取初始聚类中心,可以使聚类中心位于数据较集中的位置,并使其不受孤立点影响,另外,利用信息熵确定聚类数目,较好地解决了原始K均值聚类方法的缺点,实验结果验证了利用上述方法,可以准确判别燃气泄漏与否。
参考文献
[1] 孙立瑛, 李一博, 靳世久等. 基于小波包和HHT变换的声发射信号分析方法[J]. 仪器仪表学报, 2008, 29(8): 1577-1581.
[2] XU QingQing, ZHANG LaiBin, LIANG Wei. Acoustic detection technology for gas pipeline leaKage[J]. Process Safety and Environmental Protection, 2013, 91(4): 253-261.
[3] 孫吉贵, 刘杰, 赵连宇. 聚类算法研究[J], 软件学报, 2008, 19(1), 48-61.
[4] 胡伟, 改进的层次K均值聚类算法[J]. 计算机工程与应用, 2013, 49(22): 157-159.
[5] Bouras, C., Tsogkas, V. , Clustering User Preferences Using Kmeans[C]. 2011 Seventh International Conference on Signal-Image Technology and Internet-Based Systems (SITIS), 2011: 75-82.
[6] 李宇泊. K均值算法初始聚类中心选取相关问题研究[D]. 甘肃: 兰州交通大学, 2012.
[7] Qi chen Ma, Xiangfeng Luo, Yong Luo. Information Entropy Based the Stability Measure of User Behaviour Network in Microblog[C]. 10th International Conference on Semantics, Knowledge and Grids (SKG), 2014: 67-74.
[8] Jinhua Xu, Hong Liu, Web user clustering analysis based on KMeans algorithm[C]. 2010 International Conference on Information NetworKing and Automation (ICINA), 2010: 6-9.
[9] 吴春旭, 一种基于信息熵与K均值迭代模型的模糊聚类算法[C]. 中国管理科学学术年会, 2008: 152-156.
[10] L. Y. Meng, Y. X. Li, W. C. Wang et al. Experimental study on leaK detection and location for gas pipeline based on acoustic method[J]. Journal of Loss Prevention in the Process Industries, 2012, 25(1): 90-102.