一种BFGS校正的改进信赖域方法
2019-10-08章安阁张舸
章安阁 张舸


摘 要: 本文利用经典的信赖域方法,针对无约束优化问题,对信赖域进行改进,并在此基础上对算法进行BFGS校正。数值实验证明,相比传统的信赖域方法,改进的信赖域方法在计算效率上有了很大提高;而加入BFGS校正后,新算法相比改进的信赖域方法又有了进一步的提高。
关键词: 无约束最优化;信赖域法;BFGS校正
中图分类号: O224 文献标识码: A DOI:10.3969/j.issn.1003-6970.2019.07.020
【Abstract】: We proposed an improved trust region method with BFGS, which is based on the traditional trust region method and used to improve the trust region for unconstrained optimization problems. On this basis, the BFGS correction of the algorithm is carried out. The numerical experiments show that, comparing with the traditional trust region method, the improved trust region method with BFGS has greatly improved the computational efficiency, and compared with the improved trust region method after adding BFGS correction, the new algorithm has further improved.
【Key words】: Unconstrained optimization; Trust region method; BFGS correction
0 引言
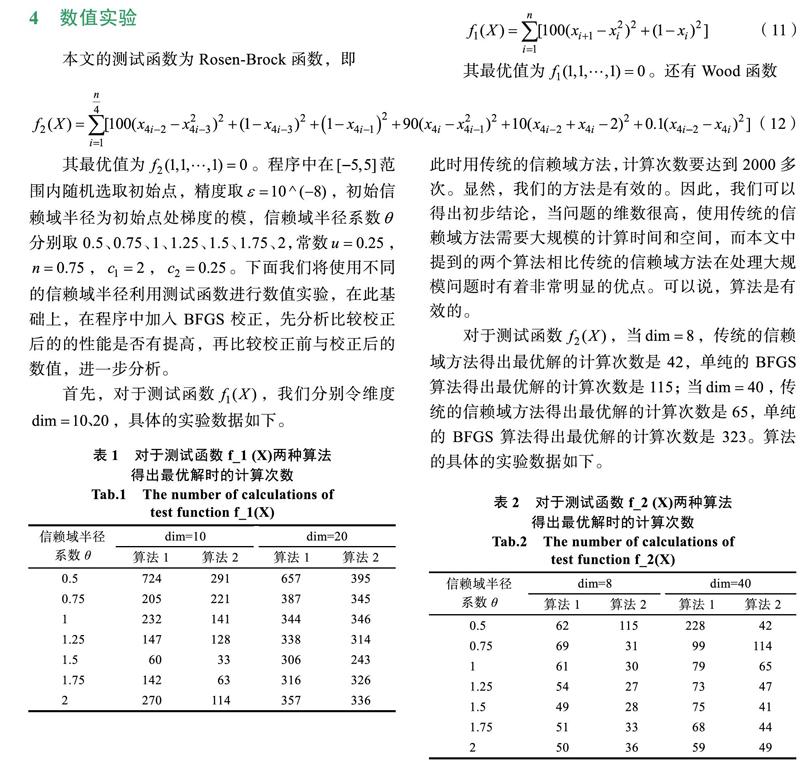
分析表1,可以看出,對于测试函数 ,当 取 时,计算次数最少;对比每一行的第二列和第三列数据,或者是第四列和第五列数据,会发现,加入BFGS校正后,计算次数也或多或少地有所下降,只有当 取 , 时次数增加了16,在可接受的范围内。但是当 时,传统的信赖域方法只需要计算21次,两种方法都不如传统的信赖域法的计算效率。但是本文提出的加入BFGS修正的改进信赖域方法(算法2)也只是稍逊于传统的信赖域方法。在维度 时,计算次数相比 时有了明显增加,但是对比之下还是当 取 时,计算次数最少;对比每一行的第二列和第三列数据,或者是第四列和第五列数据,会发现,加入BFGS校正后,计算次数也或多或少地有所下降,增加也是在1-2之内浮动。同样的,此时用传统的信赖域方法,计算次数要达到2000多次。显然,我们的方法是有效的。因此,我们可以得出初步结论,当问题的维数很高,使用传统的信赖域方法需要大规模的计算时间和空间,而本文中提到的两个算法相比传统的信赖域方法在处理大规模问题时有着非常明显的优点。可以说,算法是有效的。
对于测试函数 ,当 ,传统的信赖域方法得出最优解的计算次数是42,单纯的BFGS算法得出最优解的计算次数是115;当 ,传统的信赖域方法得出最优解的计算次数是65,单纯的BFGS算法得出最优解的计算次数是323。算法的具体的实验数据如下。
当维度较低时(dim=8),除了在θ取0.5时,次数翻了一番,当θ取其他值时,算法2相比算法1 在计算次数上有所减少,观察第三列数据,我们还可以发现当θ的值变动,计算次数的变化并不大,而且当θ取1.5时,算法2计算次数最少(28次),相比传统的信赖域法(42次)和单纯的BFGS算法(115次),都是算法2更好。;当维度升高(dim=40),除了在θ取0.75时,算法2相比算法1的计算次数有所上升,其他情况下算法2都要比算法1的计算次数少。同样的,当θ取1.5时,算法2计算次数最少(41次),相比传统的信赖域法(65次)和单纯的BFGS算法(323次),也是算法2更好。
5 总结
信赖域法和BFGS修正都是在计算优化问题时的常用方法,本文提出了一种加入了BFGS修正的改进的信赖域算法,是二者优点的一个融合。近年来,数值优化方法的发展很快,文献[1-4]都是对信赖域法进行了大量的改进,文献[5-7]更是将信赖域法与BFGS方法进行了各种糅合,本文提出的算法亦是如此,且在计算次数上有了减少。未来,针对此算法,也可以用其他的测试问题进行进一步的测试与研究。在以后的研究中,作者将亦会把本文的思想应用于最优化算法中直接法[8-10]的研究。感谢导师贺祖国教授对本文算法的宝贵意见与指导。
参考文献
G. X. Ma, “A Modified Trust Region Methods for Un-con?-
strained Optimization (in Chinese),” Master's Thesis, 2003.
J. Nocedal and Y. Yuan, “Combining Trust Region and Line Search, Y. Yuan, ed.,” Advances in Nonlinear Pro-gramming,
Kluwer, 1998, pp. 153-175.
Q. H. Zhou, Y. R. Zhang, F. X. Xu and Y. Geng, “An Improved Trust Region Method for Unconstrained Opti-mization,” accepted by Science China Mathematics.
Qinghua Zhou, Yarui Zhang, Xiaoli Zhang, “An Improved Line Search and Trust Region Algorithm” accepted by A Journal of Software Engineering and Applications, 2013, 6, 49-52.
景书杰, 张小亮. 解线性约束优化问题的自适应-BFGS信赖域算法[J]. 2010.《山西大学学报(自然科学版)》, 33(4): 500-503.
袁功林, 韦增欣. 一个新的BFGS信赖域算法[J]. 2004.《广西科学》, 11(3): 195-196, 200.
李文钰. 一类修正的BFGS信赖域方法[D]. 硕士学位论文, 2008.
M. J. D. Powell*UOBYQA: unconstrained optimization by quadratic approximation, Report No. DAMTP 2000/NA 14, University of Cambridge.
M. J. D. Powell*.The NEWUOA software for unconstrained optimization without derivatives., Report No. DAMTP 2007/NA05, University of Cambridge.
贺祖国. 混合策略的直接法研究. [学位论文]. 中国科学院: 2002.
