基于改进Center Loss函数的行人再辨识

张 璐，刘阿建

(1.武汉大学，湖北 武汉 430061；2.太原理工大学 信息与计算机学院，山西 晋中 030600)

0 引 言

常用的行人再辨识网络模型有两种：一种是基于样本对或三元组的验证网络模型。该模型由于早期公开的行人再辨识数据集较小被广泛采用，如VIPeR[1]，仅为每个身份的行人提供两幅图片；另一种极具潜力的是基于分类损失函数的分类模型[2]。该模型最初应用在图像分类中，之后受到行人再辨识研究者的青睐得益于几个大数据集的公布，如CUHK03[3]，Market1501[4]和 DukeMTMC-reID[5]。这使得训练一个更深的网络而不出现过拟合成为可能。尽管分类损失函数不仅可以充分利用数据集的标注信息，而且无需将样本进行配对，但其主要缺陷是训练目标与测试过程不一致。如训练出来的分类网络模型在进行测试时，需要将分类损失函数层移除掉(开集测试过程)。一部分研究者[6-7]结合两种损失函数的优点使行人特征具有较好的辨别性。此方法与人脸深层验证网络[8]有相类的地方，不同类的特征被分类损失函数分隔出来，同时类内距离小且类间距离大的问题被验证损失函数解决。这些方法跟目前常用的一些方法相比，在几组常用的行人再辨识数据集上有较优的表现，但是在网络训练之前，需要配对训练样本，样本种类越多，配对方式和数量越多。即使对样本进行严格的控制，但网络依然存在稳定性差、收敛慢等缺陷。

为了避免样本配对，并且使学习到的行人特征依然具有较好的判别能力，文中将Center Loss函数和分类损失函数Softmax Loss相结合，使网络在分类损失Softmax Loss与Center Loss函数的联合监督下，可以学习出更具判别性的行人特征。Softmax Loss函数将不同类分隔开，同时Center Loss函数具有和验证函数类似的功能，能使类内距离变小，使行人特征更具辨别性。文中将人脸识别函数Center Loss用于行人再辨识研究中，作用是使同类之间的差别变小，但是该函数不能解决不同类之间差距不大的问题。在同一个空间中，两个不同的类分布的很靠近或者部分重叠时，虽然每个类大部分都集中在中心点或距中心点距离较近的地方，但是辨别性依旧不太理想。因此文中对Center Loss函数进行改进，在Center Loss函数中加入类间距离变量，使类间中心最小距离变大，使其具有较好的辨别性。

1 Center Loss函数

Center Loss函数在进行网络构建的过程中，在分类网络Softmax Loss的基础上，在其特征提取层中加入损失函数Center Loss，用来计算每个类中心的欧氏距离。这样对网络进行收敛后，同一类型的样本，其行人再辨识的特征就集中在此类别的中心。这种与不加入损失函数Center Loss的分类网络相比，同类别的行人特征类内的距离更小，其中Center Loss函数的定义如下：

(1)

其中，cyi∈RD表示所属类别为yi的特征xi的中心点，并且cyi随训练批次的更新不断更新，yi样本数及特征的变化时，cyi随之更新；M表示样本数量。

另外，为了排除个别特殊样本给训练带来波动，定义中心学习率α。当网络的传播方向为反向时，其梯度LC的定义见式2，cyi的更新见式3：

(2)

(3)

其中，α∈[0,1]，如果yi=j，则δ(条件)=1，否则为0。

文中是将Softmax函数和Center Loss函数相结合，因此总损失函数表示为：

(4)

其中Softmax函数和Center Loss函数的平衡系数用λ表示。当λ=0时，则该式表示仅使用Softmax Loss函数的分类网络。

2 Center Loss函数的改进

标准的Center Loss函数在行人特征空间中，为每个类在训练过程中计算一个中心，并且使该类的特征向计算的中心点集中，其目标是减小类内距离，但是此函数不能解决不同类之间差距不大的问题。在同一个空间中，两个不同的类分布的很靠近或者部分重叠时，虽然每个类大部分都集中在中心点或距中心点距离较近的地方，但是辨别性依旧不太理想。因此在训练过程中，既考虑类内距离又考虑类间距离，通过对Center Loss函数进行改进，在Center Loss函数中加入类间距离变量，使类间中心最小距离变大，使其具有较好的辨别性。改进Center Loss函数的定义为：

(5)

因为类内中心距离矩阵具有对称性，文中将式5进行简化，即：

(6)

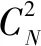
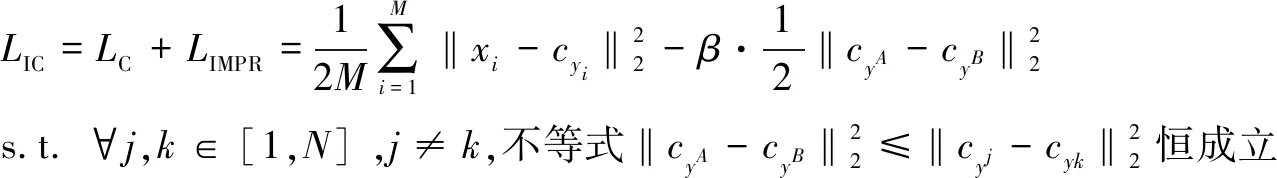
(7)

在反向传播中，LIMPR的梯度计算为：

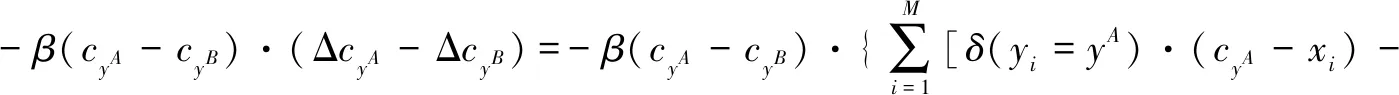
δ(yi=yB)·(cyB-xi)]}

(8)

3 实验与分析

3.1 Mnist数据集上的实验

本节通过实验展示网络学习行人再辨识特征分布的图像，直观感受改进的网络模型是否具有较优的表现，同时通过定性定量分析确定改进算法是否更加适合行人再辨识的应用。实验参考文献[9]中的Mnist数据集[10]和LeNets++网络。为了便于观察结果，将选定网络的输出维度设置为2，即学习到的行人再辨识的特征为2维，可以通过二维平面显示实验结果。实验中参数设置与文献[9]相同，除特殊说明外，实验随机选取样本图像。文中实验样本数量设置为10k。

采取四组网络模型进行行人再辨识实验，四组网络模型分别是：仅使用Softmax Loss函数作为损失函数；仅使用Center Loss函数作为损失函数；Softmax与标准Center Loss相结合作为损失函数；Softmax与改进的Center Loss相结合作为损失函数。把参数λ和β分别设置为0.1和1。图1一共四组图，分别对应上述4种损失函数。

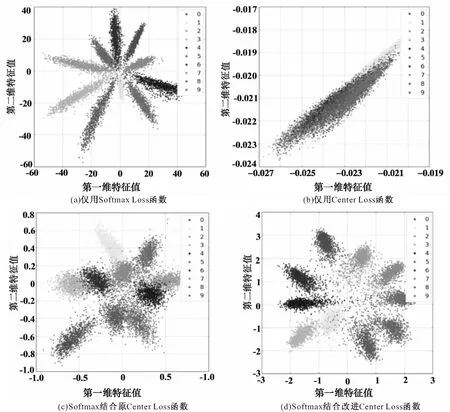
图1 Mnist数据集图像二维特征的分布

从图1(a)可知，仅使用Softmax Loss函数作为损失函数，不同类的特征之间能很好地区分开，但是同类之间的类内距离不能很好的聚集；从图1(b)可知，仅使用Center Loss函数作为损失函数，同类之间的类内距离控制在-0.03～-0.02之间，但是不同类也重叠在一起，不能很好地区别开；从图1(c)可知，Softmax与标准Center Loss相结合作为损失函数，同类之间的类内距离控制在-0.75～0.75之间，并且不同类之间没有重叠，部分已能区分开，但是部分依旧有重叠，例如类别1和类别7有部分特征重叠，这可能影响经过该网络进行行人再辨识特征的提取分类结果的准确性。从图1(d)可知，以Softmax与改进的Center Loss相结合作为损失函数，同类之间的类内距离控制在-2～2之间，同时所有不同类别的类能很好地分离开，并且类间距离比较大，在-3～4之间，使行人再辨识特征的提取更加容易。实验结果表明，在Mnist数据集和LeNets++网络基础上，改进的Center Loss和Softmax函数相结合的方法能使类内距离较小，类间距离较大，能够很好地满足行为再辨识的要求。

样本数设置为10k和50k进行实验，再对实验结果进行归一化处理，处理结果如图2和图3所示。从图2(a)可以看出，10k样本数时，提取的特征值基本能分开，但样本数达到50k时，图2(b)显示提取的特征值基本无法区分。从图3(a)和图3(b)可以看出，样本数不管是10k还是50k，都能满足类间距离较大类内距离较小的要求。由实验结果可知，Softmax与改进的Center Loss相结合作为损失函数的方法比Softmax与标准Center Loss相结合作为损失函数的方法更优，尤其是在样本数较多的情况下，改进的方法优势更加明显。

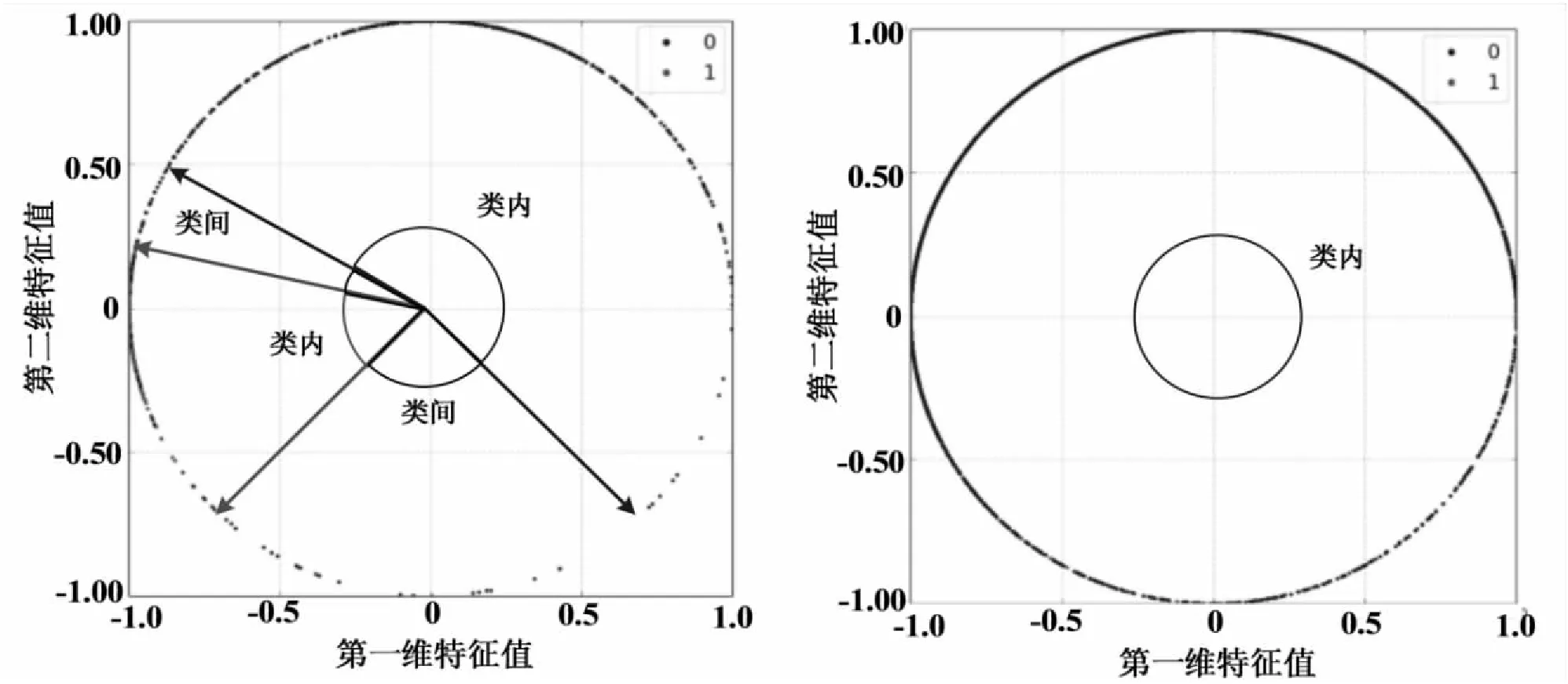
(a)10k幅图像特征分布 (b)50k幅图像特征分布图2 Softmax结合原Center Loss函数的归一化特征

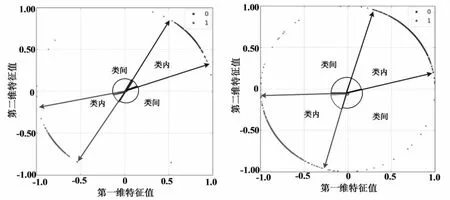
(a)10k幅图像特征分布 (b)50k幅图像特征分布图3 Softmax结合改进Center Loss函数的归一化特征

3.2 行人再辨识实验

3.2.1 数据集

选取了4个常用于行人再辨识研究的数据集进行实验，即CUHK03与Market1501、VIPeR与CUHK01[11]，其中前两个是大数据集，后两个是小数据集。CUHK03与Market1501通过DPM检测器对行人图像进行裁剪，这样的数据集更接近实际应用。另外，该实验除了Market1501均采用single-shot的测试方法，而Market1501采用的是multi-shot的测试方法。single-shot的测试方法是指在数据集中有且仅有一幅图像与目标图像来源于同一个行人，multi-shot的测试方法是指在数据集中有多幅图像与目标图像来源于同一个行人。实验的数据集均根据各自的测试协议对样本进行设置和数据集进行训练，测试报告按测试协议对测试结果取平均值。

3.2.2 数据输入准备

实验第一步是准备数据集图像，将所有图像设置成128×48的大小；然后通过所有图像计算得到训练集的均值，并把均值图像剔除出来；再通过二维变换把剩下的图像进行扩充，增长7倍；最后把幅度范围控制在-6到6之间，将图像中心设置为左边原点，随机向坐标轴方向平行移动。

3.2.3 网络框架与基本网络

文中使用的基础网络是CNN[12]与Attention-39[13](网络的详细介绍参见文献[12-13])，这种网络的主要优点是在反向传播的过程中，防止出现梯度爆炸式增长或消失不见等情况，同时有利于网络快速收敛；基本网络的最后一个全连接层输出512维的特征FC；除了全连接层，其他所有层后面都连接激活函数，该函数是线性单元且带有修正参数。

3.2.4 测试方法

因为行人再辨识是一个开集测试过程，即测试样本与训练样本的类别没有交集。因此分类子网络在测试过程中是无效的。首先通过基础网络对准备的目标图像进行特征提取，同时提取待测图像的特征；然后计算每一个待测图像特征与目标图像特征的余弦值，构建一个M×N的矩阵，其中M表示选取的目标图像数量，N表示选取的数据集图像数量。实验将特征值进行归一化处理，最后得到的余弦值就是欧氏距离。

实验采用Rank-1-5-10和mAP(mean average precision)，此方法操作方便且节省空间。并且将实验结果与当前最好的同类实验结果进行比较分析，

3.2.5 实验结果与分析

基于CUHK03数据集的实验结果见表1，表中不特殊说明，“I”表示仅使用Softmax Loss为损失函数，“I-C”表示使用Softmax Loss结合标准的Center Loss为损失函数，“I-IC”表示使用Softmax Loss结合改进的Center Loss为损失函数，CNN与Attention-39是文中选定的两个基础网络。

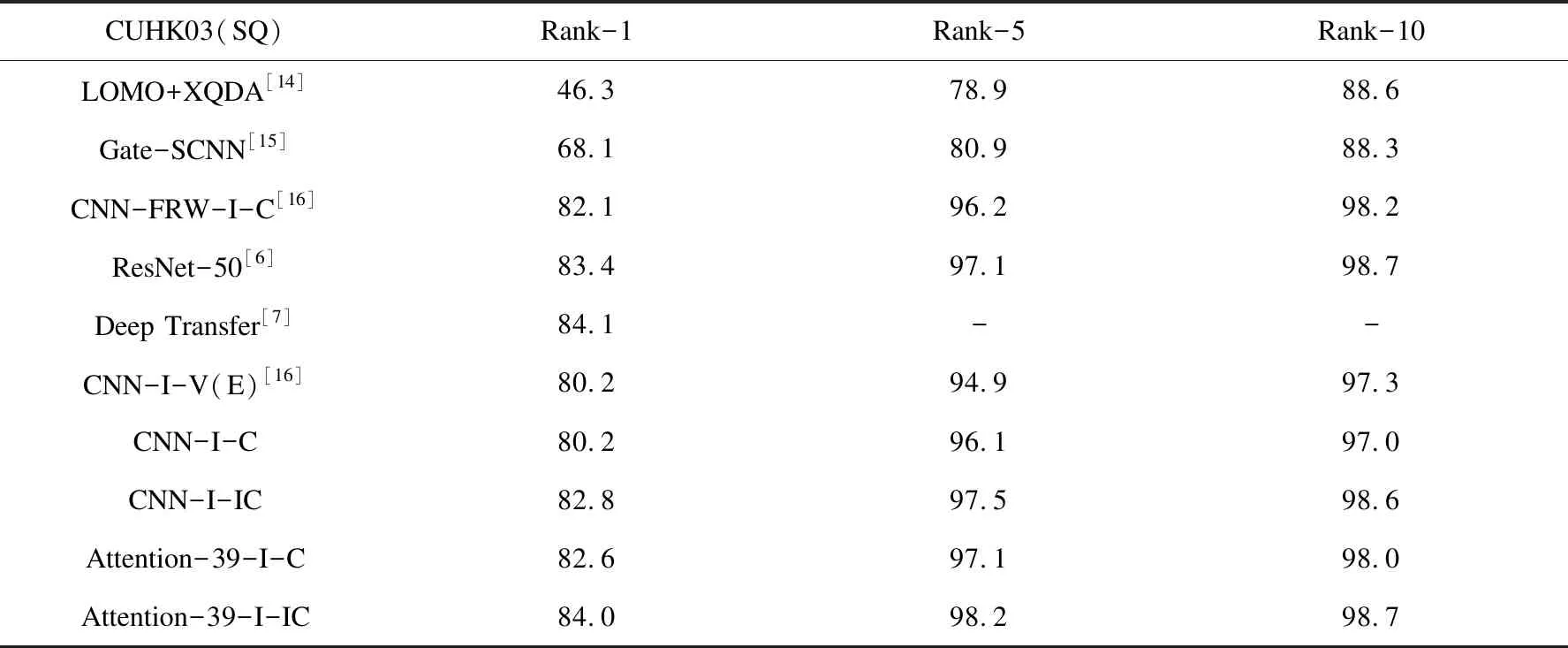
表1 CUHK03数据集上的实验结果比较

从表中结果可以看出，两种基础网络“I-C”的结果要优于“I”的结果，表明Center Loss函数能有效减小类内距离；“I-IC”的结果除了Rank-1项，其他均优于“I-C”的结果，表明文中的改进算法可以有效减小类内距离，同时增加了类间间距；“Attention-39-I-IC”算法跟当前最好的几种算法相比较，也显示出了优势。

在Market1501数据集上，文中算法同样优于目前很多算法，如表2所示。然而，在两个小数据集上的结果表明(见表3)，DNS网络模型更适用于小数据集，有较好的表现。

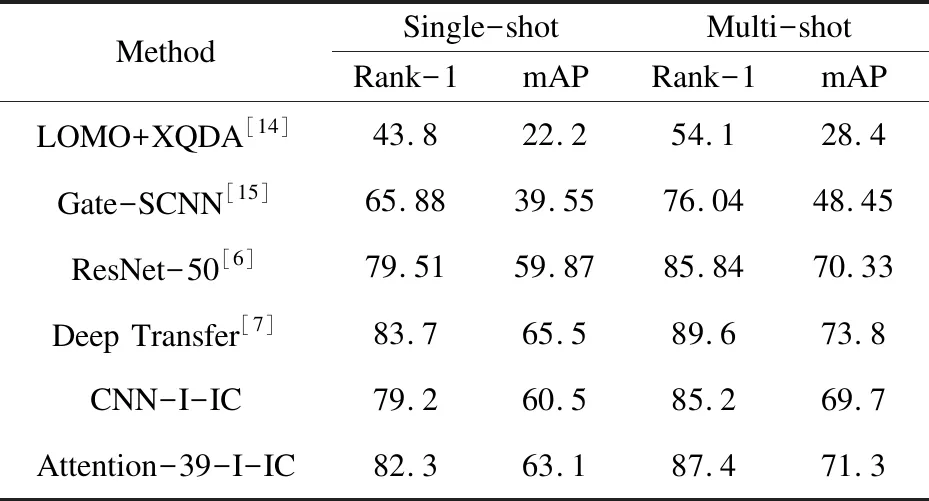
表2 Market1501数据集上的实验结果比较

从实验结果可知，Deep transfer算法表现要优于文中改进算法，原因是Deep transfer算法使用分步转化的方法，首先根据训练集精调网络模型，再进行测试。另外文改进算法在小数据集上表现一般，原因是文中算法要求充足的样本对每一个类进行训练，训练不够会引起网络的过拟合。虽然该算法在小数据集上性能不好，但是改进的Center Loss函数相比原函数，依然有一个点左右的提升。

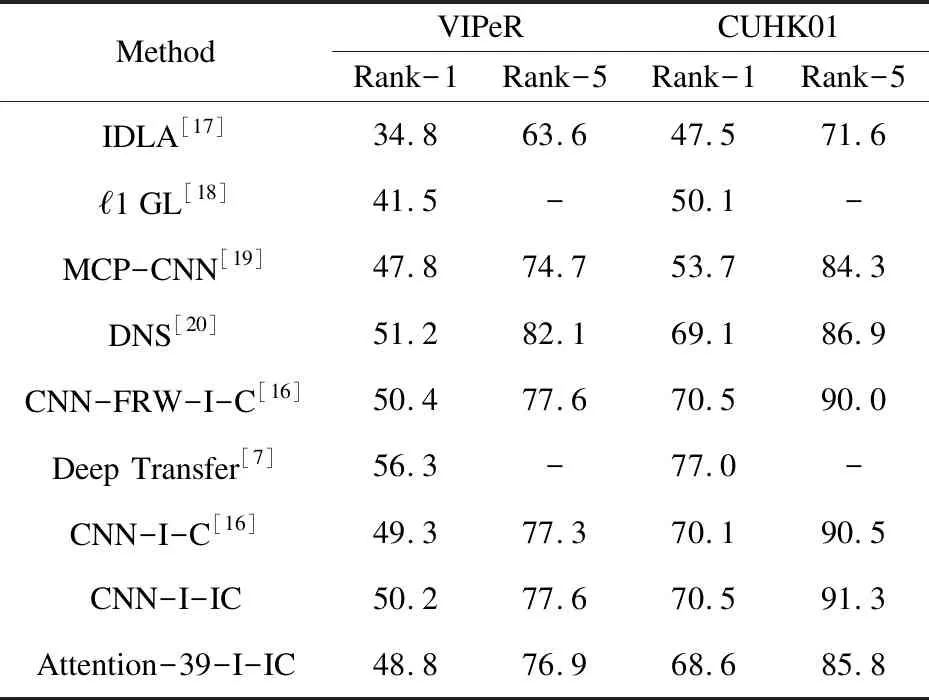
表3 VIPeR与CUHK01数据集上的实验结果比较

4 结束语

文中对行为再辨识算法进行研究，Center Loss函数能使同类类内距离较小，加入Center Loss函数的方法能使不同类之间被区分开，但由于类间间距较小，影响特征分类的准确性。所以文中对Center Loss函数进行改进，该算法满足了减小类内最大距离和增加类间最小距离的要求。实验结果表明，文中改进算法优于标准函数算法，同时也优于当前很多比较好的算法，特别是在大数据集上表现更加明显。