基于WNN-SVM的水文时间序列预测方法研究

余 洋，万定生

(河海大学 计算机与信息学院，江苏 南京 211100)

0 引 言

在大数据时代，数据已经成为重要的资源。面对海量的数据，对其进行有效的处理和分析变得非常重要[1]。而时间序列数据挖掘(time series data mining，TSDM)已成为数据挖掘领域的重要分支，主要通过不同的数据挖掘技术[2]分析时间序列的局部特征从而挖掘出时间序列内在的规律，这将有助于实现时间序列的异常检测、预测等目的[3]。

而具有随机性、突变性的复杂时间序列如水文时间序列的预测已成为国际热点。此类时间序列预测方法主要有三类：一是定性预测方法，根据预测对象的特性、状态，采用类推对比、专家打分等方法来预测序列；二是因果关系预测法，对目标时间序列和影响因子序列基于因果关系进行统计预测；三是时间序列预测法，根据时间序列自身变化规律进行预测，常见的有自回归模型(AR)、自回归滑动模型(ARMA)[4]、人工神经网络(ANN)、相空间模型、灰色理论和支持向量机(SVM)等。Kottegoda[5]提出在线性随机模型中ARMA对Vanern河流量进行了预测，但其在非平稳序列中的表现不够精确。Wei Shouke等[6]将小波神经网络应用于江河月径流量拟合和预测上，得出WNN相对于后者能显著增加预测精度的结论，但其对多变化的流量精度仍有缺陷。

由于这些模型的适用范围不同，而此类复杂时间序列既包含线性成分又含有非线性成分，对单一模型的优化不能完全克服其局限性[7]。针对此问题，文中提出了基于WNN-SVM组合的水文时间序列预测模型。

1 支持向量机和小波分析

1.1 支持向量机

支持向量机(support vector machine，SVM)是一种基于统计学习理论构建的典型神经网络，它的基本思想是使用一个线性模型解决非线性的问题，将一些非线性的输入空间映射到高维的特征空间。利用最佳的超平面构造边界，使决策类之间实现最大分隔，在新的空间构建一个线性模型表示原来空间的非线性决策边界，最后转化为一个凸二次规划问题进行求解。在线性可分的情况下，二元决策类分离表示为：

y=ω0+ω1x1+ω2x2

(1)

其中，y为输出向量，xi为特征值，ωi为平面的权重值。

支持向量机将输入转换成高维特征空间，以构造一个线性模型来实现非线性类边界。在非线性可分的情况下，高维的最大超平面边界方程可以表示为：

(2)

其中，K(x(i),x)为核函数。输入空间中产生的不同类型的支持向量机有不同的核函数，常见的核函数有多种，例如多项式核和高斯径向基核等。

1.2 小波分析

1.2.1 小波变换

小波(wavelet)是一种特殊的长度有限，平均值为0的波形。它的“小”体现在时域具有紧支性或近似紧支性，它的“波”体现为正负交替的波动性，即直流分量为零。小波变换(WT)利用信号在一簇基函数构成的函数空间的投影表征该信号。在低频部分具有较低的时间分辨率和较高的频率分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，能实现信号的多分辨率分析，得到信号的等价描述[8]。小波变换可分为连续小波变换(CWT)和离散小波变换(DWT)[9]。

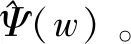
(3)

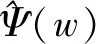
(4)

其中，a是尺度因子；b是位移因子。

定义2：任意L2(R)空间中的一维信号f(t)作离散小波变换的表达式为：

Wf(j,k)≤f(t)

(5)

1.2.2 紧致型小波神经网络

小波神经网络(WNN)从结构上分为两大类[10]，一类是小波变换与神经网络松散耦合形成的松散型小波神经网络。整个系统由小波变换和神经网络以串联形式构成。小波分解作为神经网络的前置处理手段[11]。另一类是小波变换与神经网络紧密融合形成的紧致型小波神经网络[12]。文中采用的是第二种，其基本思想是以小波分析中的小波基函数代替BP神经网络中的Sigmoid族激活函数，并以小波函数的尺度因子置换输入到隐含层的权值，以位移因子置换隐含层阈值。紧致型WNN由输入层、输出层和隐含层组成，信号前向传播，误差反向传播。其表达式为：

(6)

2 WNN-SVM组合预测模型

具有随机性、突变性的复杂时间序列如水文时间序列的确定性成分、周期性成分和非确定性因素，使得单一模型及其改进对预测精度的提升空间十分有限。传统时间序列模型对序列平稳性要求较高且预测效果不尽人意，对此提出一种基于小波变换的组合预测模型。与传统的以权系数最优为目标的组合预测方法不同，通过引入小波变换，使得序列的高低频成分分离，针对高低频序列特征，分别采用不同的预测算法。以水文时间序列为例，其建模流程如图1所示。

2.1 均值归一化

复杂时间序列普遍波动频繁且差值较大，因此首先有必要对时间序列进行归一化处理以减小模型误差。处理数据的归一化方法通常为线性函数归一化(Min-Max scaling)和0均值标准化(Z-score standardization)，但由于水文时间序列数据在个别处峰值极高，采用线性函数归一化方法会导致大多数数据处于一个极低的值，损害模型的训练，甚至导致梯度消失或爆炸；而0均值标准归一化方法则要求原始数据的分布近似为高斯分布，否则归一化的效果会变得很糟糕。

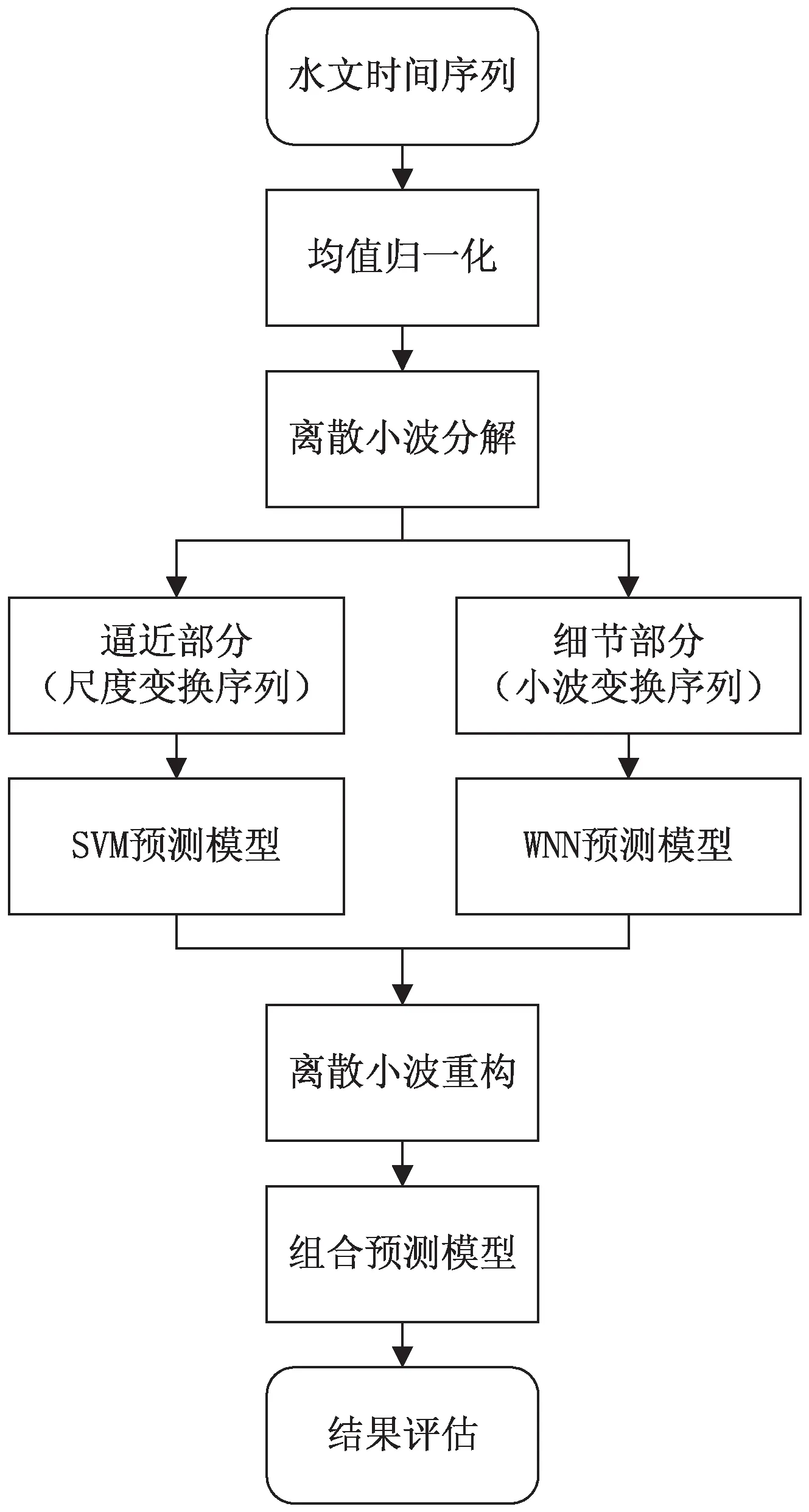
图1 组合预测模型建模流程

因此，提出一种基于均值的归一化方法，经验证其有效规避了梯度消失和梯度爆炸，具有较好的训练效果。归一化公式如下：

(7)

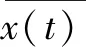
2.2 组合预测模型建模

算法思想：在对时间序列进行预处理后，通过相空间重构的方法将低维时间序列向高维转换。随后对时间序列信号进行小波分解，有助于发挥小波的多分辨率分析优势，同时也是组合模型并行预测的必要步骤。结合子序列的波形特征和波动频率，针对波动性很高的高频小波变换序列，用WNN模型对其进行拟合预测，能有效提高预测的准确性。针对包含趋势项和周期项的低频尺度变换序列，利用SVM模型预测其未来值，同时能降低计算量。最后将子模型输出的预测值序列进行小波重构，得到预测值。

算法步骤：

(1)对原始复杂时间序列进行去噪、均值归一化等预处理。

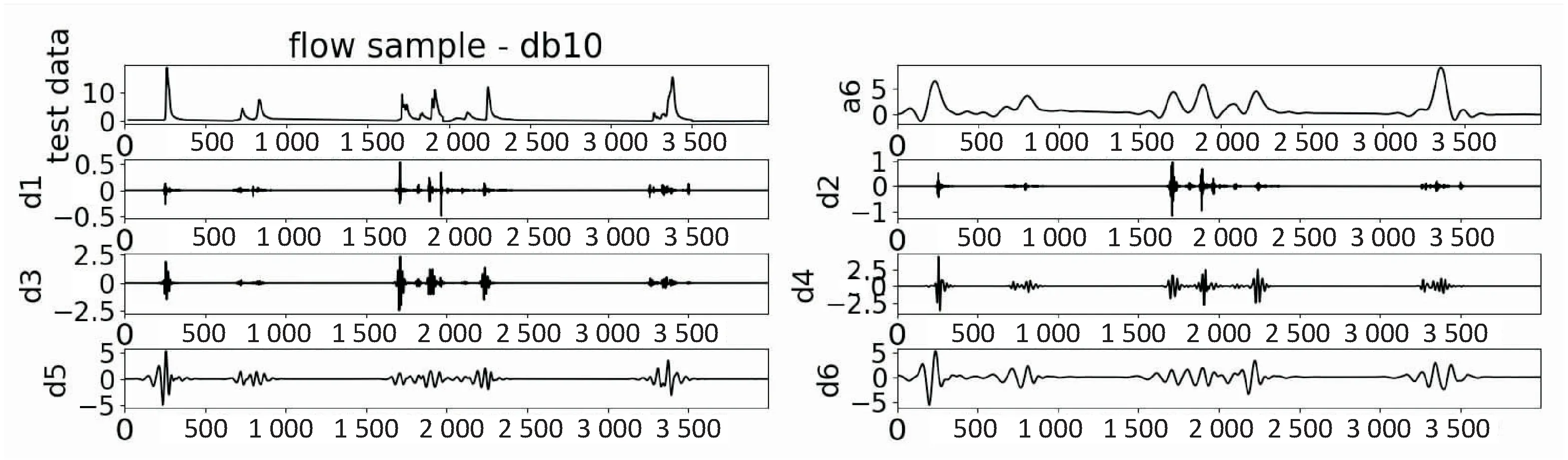
(2)对清洗后的时间序列数据进行小波分解，得到不同频段的小波。小波分解函数通常按照自相似原则和小波支撑集长度进行选择。大部分应用选择支撑集长度为5～9的小波，因为支集太长会产生边界问题，支集太短消失矩太低，不利于信号能量的集中。朱跃龙等[13]采用db10小波作为流量预测时的分解小波，因Daubechies(db)小波适合提取时间序列跃变特征，而实验流域流量序列细节波动与db小波非常相似，因此选择db10小波作为原始时间序列分解的小波基，分解层级为6。分解算法见算法1，重构算法见算法2。

算法1：Signal_Wavedec(db,sourceData)。

输入：db：过滤器类型；sourceData：归一化时间序列。

输出：cA[n]：分解后的近似部分序列-低频部分；cD[n]：分解后的细节部分序列-高频部分。

for(n=0 to decLen) do

cA[n]=0,cB[n]=0；//遍历小波变换结果序列长度,初始化分解序列

for(k=0 to filterLen) do

p=2*n-k；

if((p<0)&&(p>=-filterLen+1))

tmp=sourceData[-p-1]；

else if((p>dataLen-1)&&(p<-dataLen+filterLen-2))

tmp=sourceData[2*dataLen-p-1]；

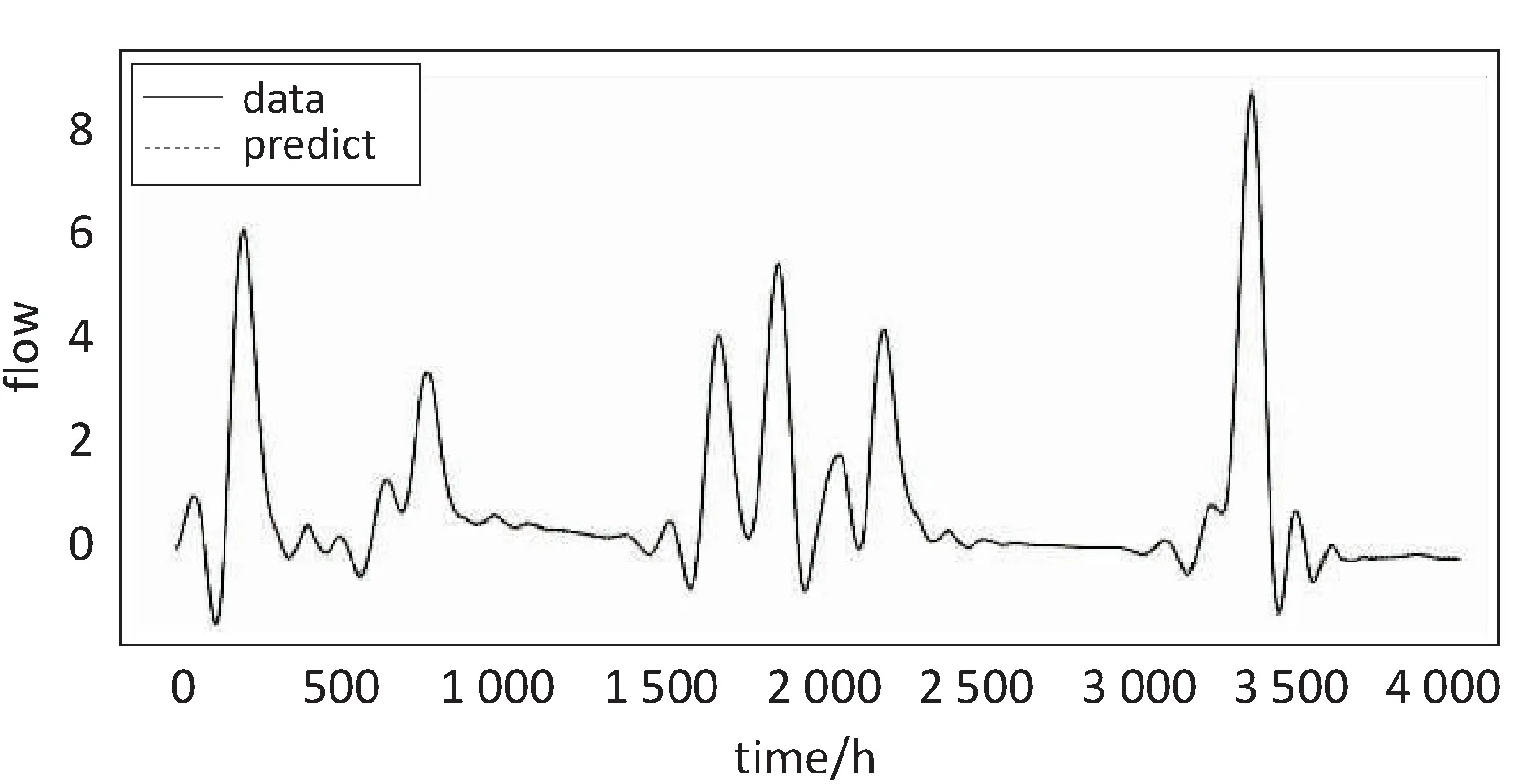
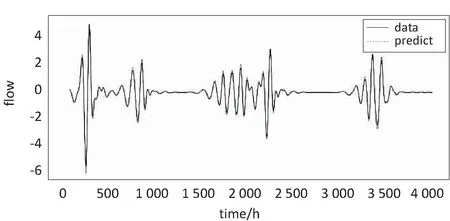
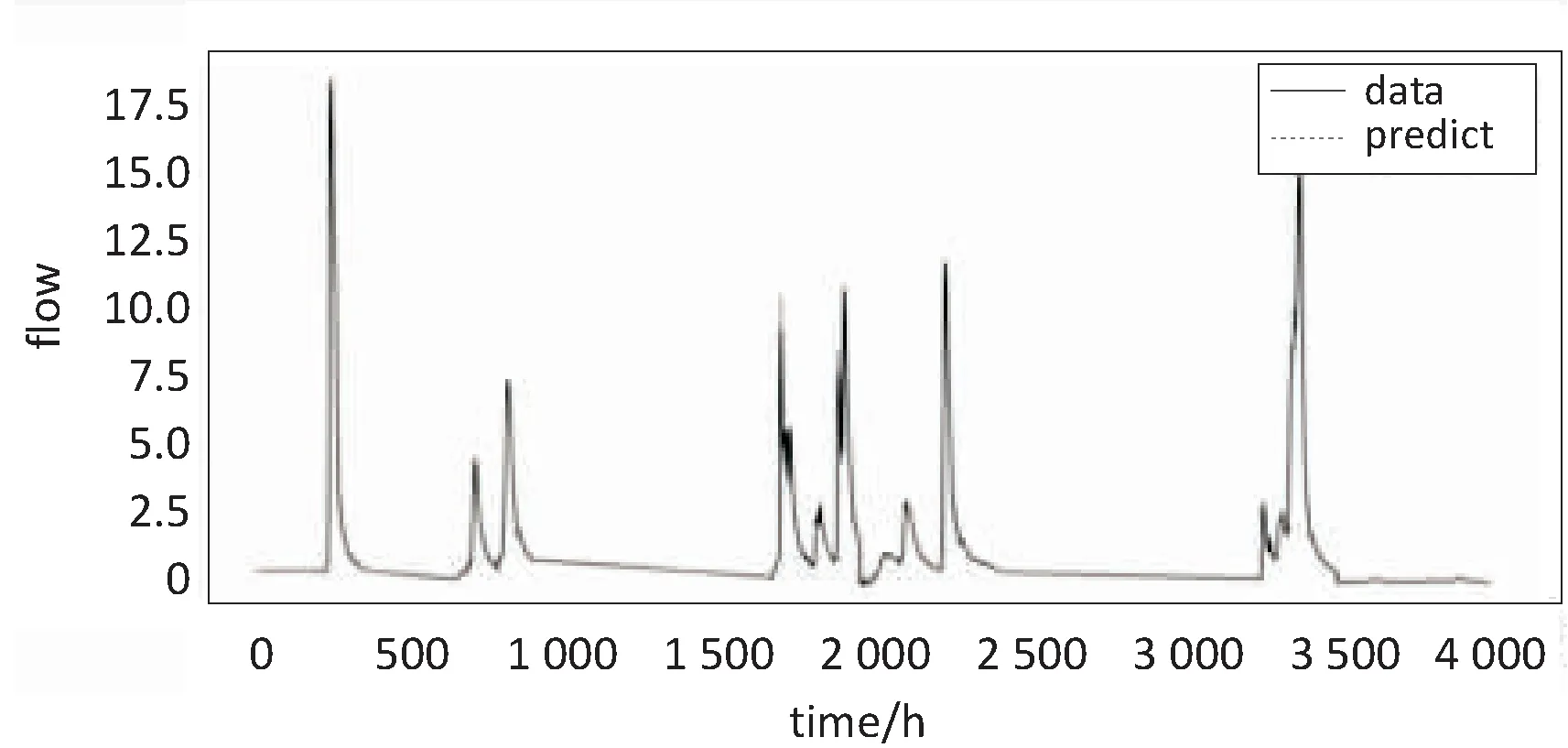
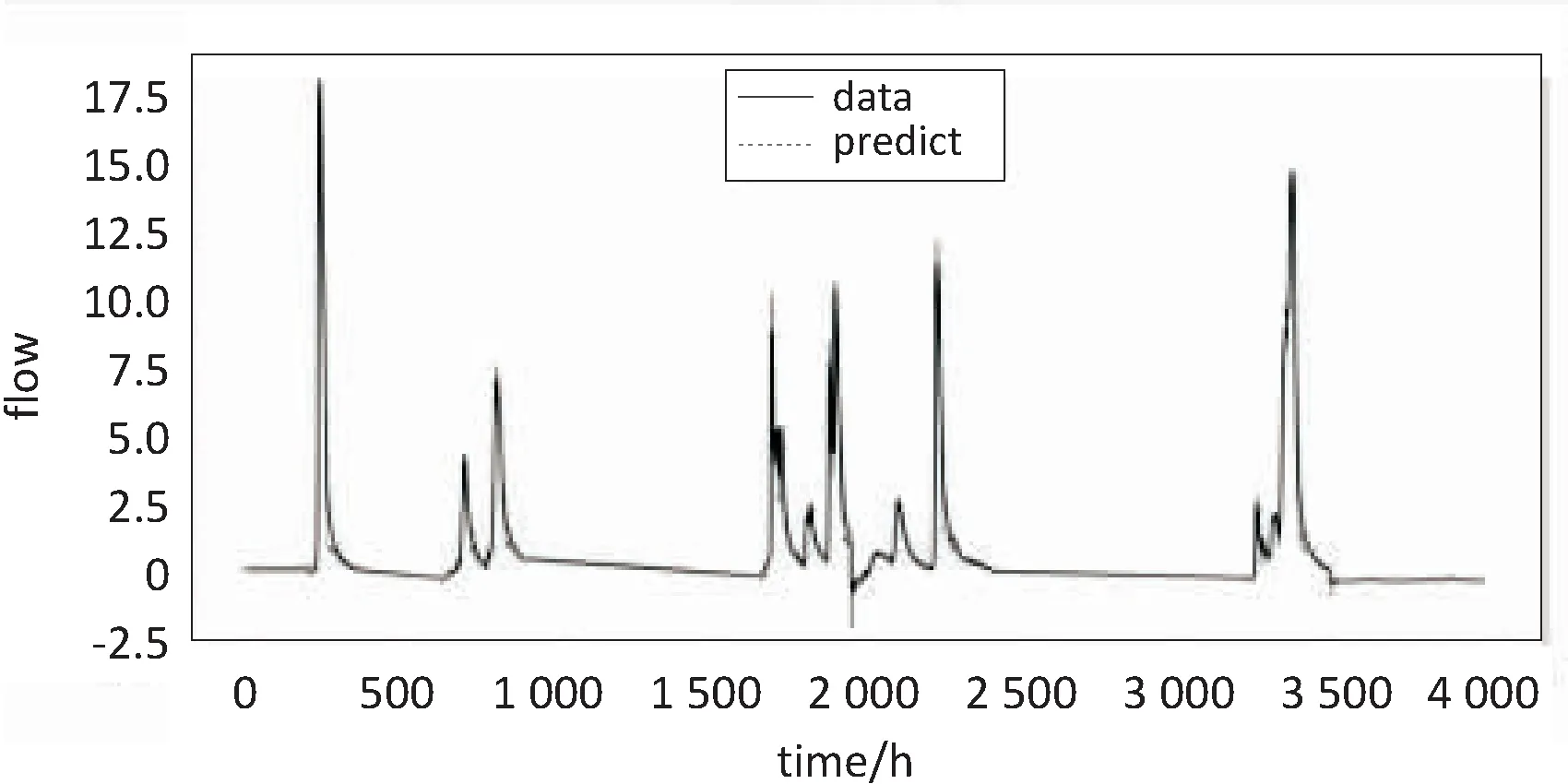
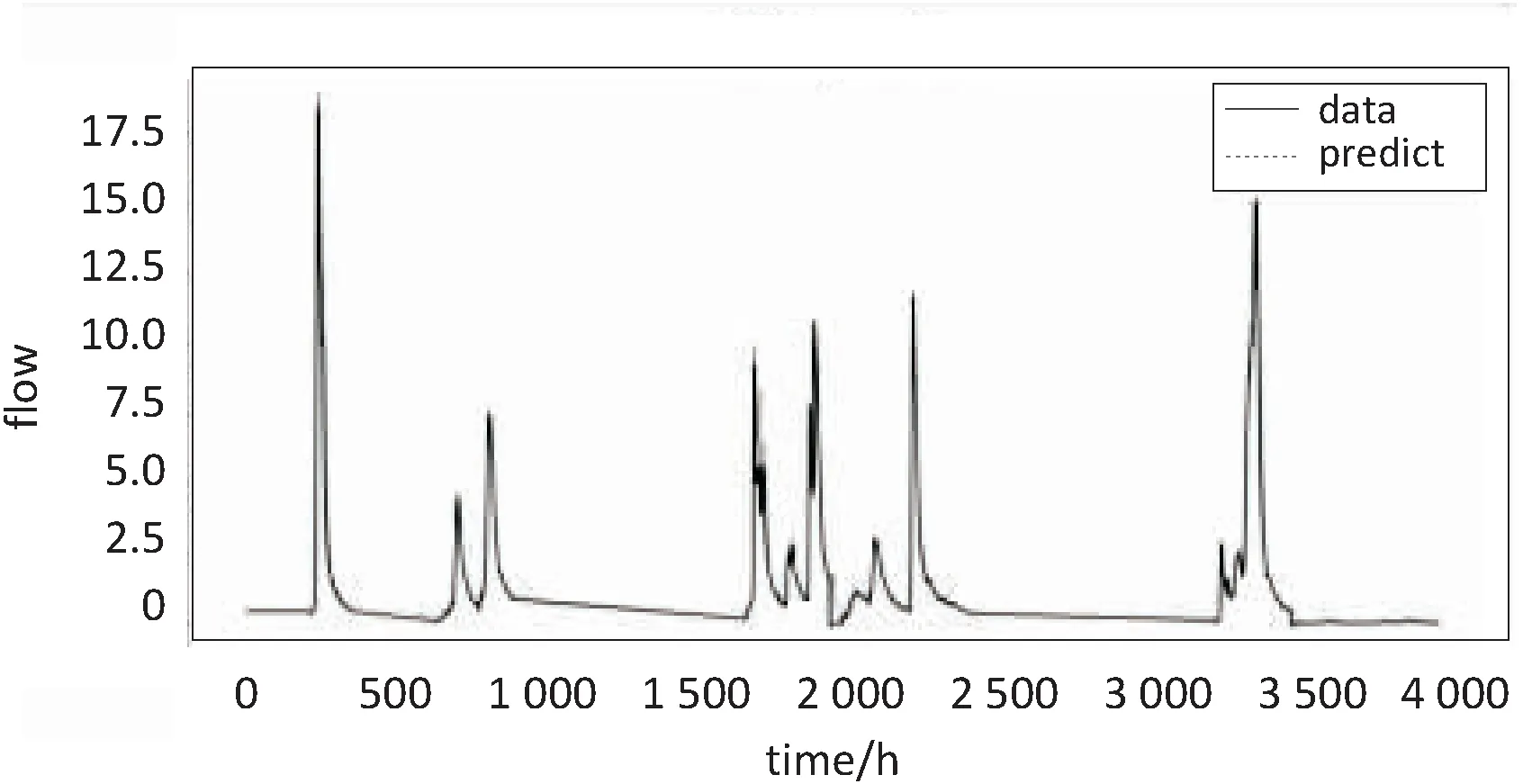
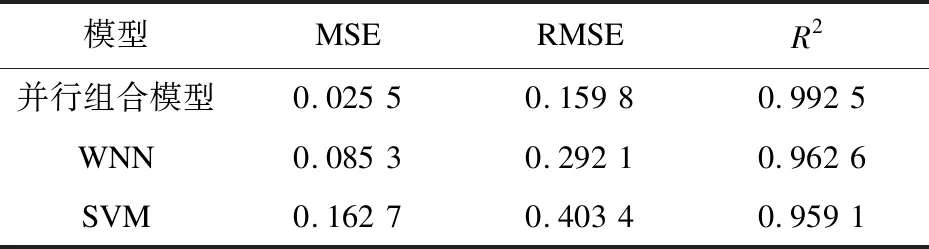
else if((p>=0)&&(p

tmp=sourceData[p]；

else tmp=0；//信号边沿对称延拓

cA[n]+=m_db.lowFilterDec[k]*tmp；

cD[n]+=m_db.highFilterDec[k]*tmp；

end for

end for

算法2：Signal_Waverec(cA,cD,db)。

输入：db：过滤器类型；cA，cD：分解后的低频高频序列。

输出：recData：重构后输出的数据。

for(n=0 to recLen) do

recData[n]=0//遍历小波变换结果序列长度,初始化重组序列

for(k=0 to cAlength) do

p=n-2*k+filterLen-1；

if((p>=0)&&(p

recData[n]+=m_db.lowFilterRec[p]*cA[k]+m_db.highFilterRec[p]*cD[k];//信号重构

end for

end for

(3)在时间序列数据分解后对各子序列进行相空间重构[14]，由此可以将低维时间序列向高维转换，尽可能挖掘到序列间的相关信息[15]。设时间序列为x(t)，t=1,2,…,N，嵌入维为m，时间延迟为τ，则重构相空间为：

y(t)={x(t),x(t+τ),…,x[t+(m-1)τ]},t=1,2,…,M

(8)

其中，M=N-(m-1)；τ为相空间中的相点数。实际应用中，若时间延迟τ太小，则相空间矢量在数值上过于接近，无法提供两个独立的坐标分量；若时间延迟τ太大，则两坐标分量的相关关系又趋于独立，根据自相关函数法分析，选定τ=1，m=25。

(4)针对分解后的低频尺度变换序列构建支持向量机模型进行预测。普遍认为，基于高斯核函数的支持向量机具有较好的模拟效果[12]，实验选取高斯核函数(RBF)作为支持向量机模型的核函数，定义为：

K(x,xc)=exp(-g‖x-xc‖2)

(9)

模型中惩罚参数C设置为10.0，不敏感损失函数ε设置为0.1。将相空间重构后的二维数据输入至模型中进行训练，并对测试数据进行预测。

(5)对小波分解后的高频小波变换序列应用小波神经网络进行预测。小波神经网络输入维数和小波函数是影响网络性能的重要因素[16]。通过对小波系数进行相关性评价，发现嵌入维m=25，时间延迟τ=1时，具有较高的相关性。经测试选取小波函数为Morlet小波，其基函数和导函数分别为：

Ψ(x)=exp(-x2/2)*cos1.75x

(10)

Ψ'(x)=-(xcos1.75x+1.75sin1.75x)*

exp(-x2/2)

(11)

随后设计小波神经网络的结构。根据相关性分析设置输入层节点数为128，输入维度为25，隐含层数为1，输出层节点数为1，优化器为Adam函数，损失函数为MSE，验证数据集为训练数据集的10%，最大迭代次数为100。进行网络迭代训练得到WNN模型。具体过程如算法3。

算法3：WNN_premodel(train,test)。

输入：train：小波变换序列训练集；test：小波变换序列测试集。

输出：测试集预测值test_simu。

初始化参数：输入节点数m，输出节点数N，隐含节点数n，训练样本数S，迭代步长etha，最大迭代步数StepMax；

G<-normrnd(0,1,n,m+1),W<-normrnd(0,1,N.n+1)； //权值系数矩阵随机初始化

while(flag==0) do //未达到训练要求或迭代步数

WaveNetIn<-G*[X;ones(1,S)]；

V<-ψ(x)；//小波函数基函数

Y<-tansig(W*[V;ones(1,S)])；//计算WNN输出

if(Step>=StepMax) flag<-1；//退出

else

dtansigWV<-4*exp(2W[V;ones(1,S)])/(exp(2W[V;ones(1,S)]+1)^2)；

W<-W-etha*(-(dtansigWV*EA)*[V;ones(1,S)]’)；//输出层系数矩阵更新

DL<-ψ'(x)；//小波函数导函数

dEdG<- -DL*(W(:,1:n)’*Gamma)*[X;ones(1,S)]’；

G<-G-etha*dEdG；//输入-隐含层权值系数矩阵更新

end if

end while

3 实验及结果分析

3.1 实验结果

实验平台为PyCharm2017.3.4，采用的数据集为屯溪流域从1981年5月1日至2007年3月25日共计43 996个小时流量数据。数据集被分为两部分，一部分是训练数据共39 998条，用于训练调整网络权值和系数；另一部分是测试数据共3 998条，用于测试网络性能。

对归一化流量序列进行离散小波变换，采用Mallat算法，小波的低通滤波长度不能太长，同时能提取序列跃变特征，采用db10小波作为小波分解函数，分解层级为6层，分解后的低频尺度变换序列为a6，高频小波变换序列为d1，d2，d3，d4，d5，d6。因为随着分解层级的提高，每次循环抽样都会减少低频近似分量的数据量，因此对分解后序列应进行单支重构，便于预测。测试数据分解序列如图2所示，训练数据与其相似。

图2 测试数据流量时间序列小波分解

利用SVM模型对尺度变换序列a6进行仿真预测，得到SVM模型对测试数据a6序列的拟合及预测结果如图3所示。

图3 SVM模型预测a6序列效果

依次导入训练数据的d1，d2，d3，d4，d5，d6序列，对WNN进行网络迭代训练，在迭代次数不到50次时损失函数值已趋于稳定，说明WNN的收敛速度良好；利用训练好的WNN对测试数据集的3 998个样本进行测试，其中对d6小波变换序列的预测效果如图4所示。

图4 WNN模型预测d6序列效果

将SVM子模块和WNN子模块得出的预测结果进行重构，即可得到组合模型的预测结果。将尺度变换序列a6和小波变换序列d1，d2，d3，d4，d5，d6的预测值进行重构得到组合模型的输出，如图5所示。

图5 WNN-SVM组合模型预测效果

同时，应用单一的WNN模型及SVM模型对流量序列进行预测，得到的预测序列如图6、图7所示。

图6 WNN模型预测效果

图7 SVM模型预测效果

将基于小波变换的并行组合模型与单一的WNN模型以及SVM模型的预测值进行对比，同时选择均方误差(MSE)、均方根误差(RMSE)和决定系数(R2)对上述模型的预测效果进行参数检验，得到的参数统计结果如表1所示。

表1 模型性能对比

3.2 实验分析

通过实验验证，SVM模型对尺度变换子序列的拟合程度与WNN模型对小波变换子序列的拟合程度都处于较高的水平。同时，文中提出的WNN-SVM组合模型对测试序列的拟合程度非常贴近原始序列真实值。而SVM模型和WNN模型在整体上虽然保持了一定的准确性，但在波动转折点具有一定的迟滞性，导致较大误差。在参数检验上，MSE、RMSE越贴近0，则预测效果越好，R2则越贴近于1，表示拟合程度越高。可以看出，并行组合模型的MSE和RMSE明显低于WNN和SVM模型的MSE和RMSE，而R2值则比WNN和SVM模型更贴近于1，验证了其预测能力，相对单一模型具有更好的性能表现。

4 结束语

针对单一模型对具有随机性、突变性复杂时间序列预测精度的不足，提出一种基于小波变换的组合预测模型，将SVM模型与WNN模型相结合的组合模型应用于测试屯溪流域的小时流量数据。为验证方法的有效性，将其与传统的单一WNN模型和SVM模型进行对比，经实验验证组合模型的预测精度高于单一模型，证明了该并行组合模型的有效性。但对于小波基函数及分解层次的选择，仍依赖于实验对比分析。同时，对复杂时间序列预测期的延长还有待后续研究。