基于电信大数据的信用卡精准营销算法研究及应用

成 晨，韩玉辉，程新洲，张 恒（中国联通网络技术研究院，北京100048）

1 概述

随着机器学习、AI技术的研究和推广以及5G万物互联时代的到来，大数据技术已逐渐成为行业技术革命的新动能，运营商大数据则以其用户规模巨大、覆盖空间广、时间连续性强的优势发挥着重要作用。通过运营商大数据，我们可以获取业务行为、时间位置、使用偏好、终端等信息，形成用户360°画像，为垂直领域带来新思路和新动能。

在金融行业中，信用卡业务是银行零售业务利润贡献的重要组成部分，也是促进产品和服务供求方交易的良性循环的催化剂，而信用卡本身也是联系银行、客户、特约商户等多方关系的重要渠道，其客户类别和客户需求呈现多元化、个性化的特征，因此精准挖掘潜在信用卡用户对银行增加收入、开拓市场、构建生态链有着重要意义。基于运营商大数据及机器学习算法，可以深刻洞察信用卡用户及意向用户的特征，将潜在客户转变为实际客户，从而增加银行信用卡业务收益。在此过程中，基于客户特征划分用户群体，并获取影响意向率和转化率的关键因素，具有重要意义，聚类算法是解决此类群体划分问题的常用方法。

K-means算法是经典的聚类算法，该算法以样本之间的距离作为衡量样本是否相似的指标，先假设簇是由距离相近的样本组成，通过对簇划分的优化，使簇内距离之和最小，也就是找到簇间独立且簇内紧凑的簇群。因此，通过K-means算法可以对信用卡用户及潜在用户群体进行聚类，基于每个簇的特征获取影响意向率、转化率和核卡率的关键因素，更加有的放矢地进行信用卡推广。

在K-means聚类算法中，第1步为簇头的选择，在所有的节点中随机选择k个节点作为簇头，然后根据簇内节点的位置更新簇头，因此，若初始簇头的选择不合理，将会影响最终聚类结果。而群体智能算法有着良好的健壮性，可以有效解决这类多模态、非线性的np-hard问题。

2 基于人工蜂群算法的K-means聚类算法

2.1 K-means聚类算法

K-means算法是经典的聚类算法，其根本目标是通过对簇划分的优化，使簇内距离之和最小。假设在集合{Y}，y1，y2，…，yn中有N个个体，聚类目标是把N个个体划分为k个簇，表示为U={u1，u2，…，uk}，使划分结果中簇内的个体间的距离最小。步骤如下：

a）在集合{Y}中，选择k个节点u1，u2，…，uk作为初始簇头。

b）把另外N-k个非簇头节点分配到k个簇中，使每个节点与簇头的距离之和最小。

c）基于步骤b）的分类结果更新k个簇头，如公式（1）所示：

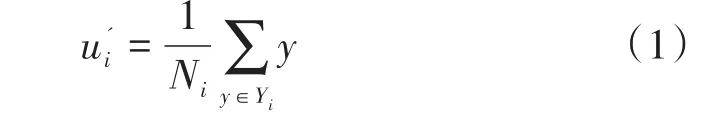
其中，Ni表示簇 Yi中第 i个体，表示更新后的第i个簇头；

由此可以看出，在K-means聚类算法中，第1步是选择k个初始节点作为k个簇的中心，在后面的进化中，根据簇内节点的位置更新每个簇的中心，如果在某一次进化后，簇内距离与簇间距离的比值没有发生变化，则迭代结束。因此k个聚类中心的初始化对聚类结果有较大影响，若随机生成的k个聚类中心不合理，可能会导致聚类效果不佳。

2.2 人工蜂群算法

群体智能算法为解决K-means算法的簇头初始化问题提供了可行方案。群体智能算法的灵感来自于群居性动物利用个体间的协作所表现出的宏观智能行为，其结构为分布式、并行性、不存在中心及控制器，可用于解决目标确定的np-hard问题，包括细菌觅食算法、蛙跳算法、粒子群算法、蚁群算法等等。人工蜂群算法（Artificial bee colony algorithm）是基于群体智能的一种典型算法，其基本思想为蜂群通过个体之间的信息交流和分工合作完成蜂蜜采集，算法以适应度函数作为进化的依据。该算法由蜂蜜源（Source）、引导蜂（Leader）、侦查蜂（Scouter）和跟随蜂（Follower）4个要素组成，步骤如下：Leader发现Source并共享信息；Follower根据Leader提供的信息以一定的概率进行搜索；如果Leader多次搜索到的Source没有改善，则放弃现有蜜源，其角色转化为Scouter寻找新的Source，当搜索到高质量的Source时，再转化为Leader。

由上可知，角色转换是人工蜂群算法特有的机制，与蛙跳算法、粒子群算法等群体智能算法不同，它通过Leader、Follower和Scouter三者的角色转换及群体协作的方式寻找高质量Source，其中Scouter用于避免算法陷入局部最优解，Leader用来维持当前最优解，Follower用来提升搜索效率。

在人工蜂群算法的实施过程中，假设解空间维度为K，则Source的位置表示为式（2）：

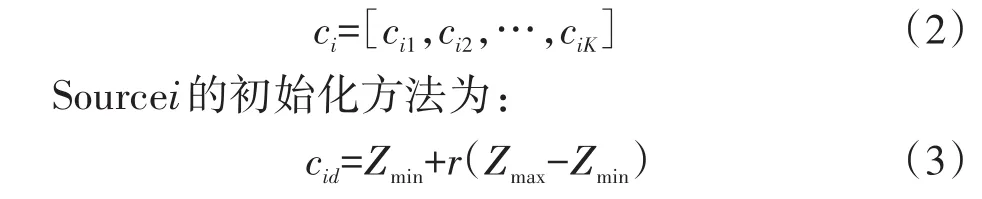
其中 r=rand（0，1），Zmin≤xik≤Zmax，Zmin和 Zmax分别表示解空间最小值和最大值，cid表示第i只蜜蜂源的第d维空间的值。

在初始阶段，Leader在Sourcei周围产生一个新的Source，方法如式（4）所示。

其中j≠i，u∈［-1，1］，服从随机分布，wik表示第 i只引导蜂的第k个解空间的值。则新产生的第i只Source表示为：

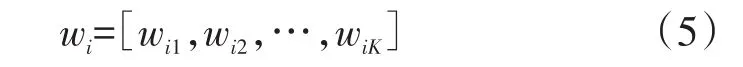
其适应度表示为F（ci），F（ci）计算方式由具体问题确定。以最小化优化问题为例，若F（wi）＜F（ci），则按照贪婪选择机制用wi代替ci，否则保留ci。所有的Leader按照式（4）进行更新后，返回交流区同步各自的信息，随后Follower按照式（6）计算更新概率：

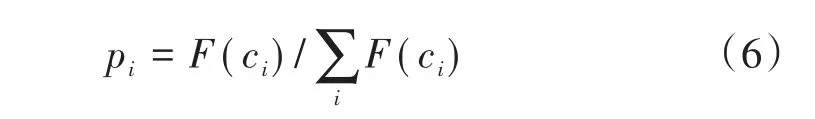
随后，随机产生 ri，ri∈［0，1］。若 ri＞pi，则基于式（3）产生新的Source。

设迭代次数为T，在搜索过程中，若Source ci经过T次迭代后并未找到更好的Source，则它将会被丢弃，它相应的Leader转化为Scouter角色。Scouter在定义域内随机产生一个新的蜜蜂源，如式（7）所示：

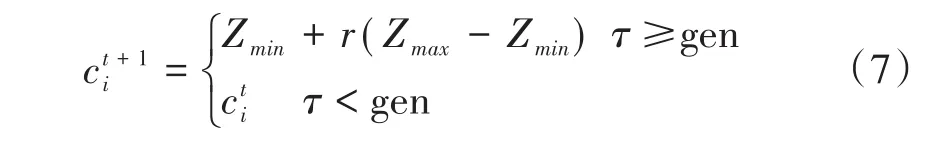
其中，τ为尝试次数，gen为最大尝试次数。

综上所述，人工蜂群算法的步骤为：

a）设定参数gen，解空间个数P，解维度K以及最大迭代次数T，初始化Source ci。

b）为每个Source ci分配一个Leader，按照式（3）搜索，产生新的Source wi。

c）适应度计算，根据贪婪算法确定是否保留该Source。

d）根据式（5）判断ci是否被保留以及Leader是否转换为Scouter。

e）Follower按照式（6）进行搜索，根据贪婪算法确定是否保留Source。

f）判断是否放弃ci，若是，将Leader转化为Scouter，若否，则进行步骤h）。

g）根据式（7）生成新的Source。

h）判断是否达到最大迭代次数，若是，终止迭代，输出最优解；若否，返回步骤b）。

基于sphere函数将人工蜂群算法与粒子群算法进行性能对比，采用式（8）所示的测试函数。

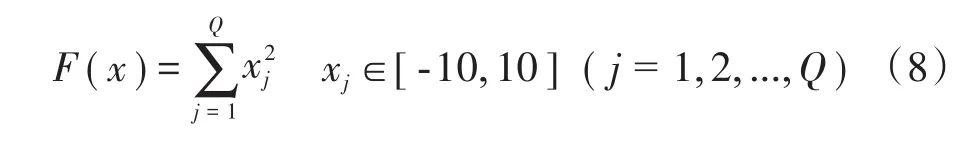
其中Q为算法中初始解的维度，F（x）为适应度值。

在迭代初期，粒子群算法比工蜂群算法收敛速度快，但是，由于人工蜂群算法引入了角色转换机制，使得算法更容易跳出局部最优解，在全局范围内进行优化，故人工蜂群算法有更高的收敛精度，有更强大的全局搜索能力。

2.3 基于人工蜂群算法的K-means聚类模型

把人工蜂群算法引入K-means聚类算法的簇头初始化过程中，其步骤如下：

a）初始化样本总数为N，簇头个数k。

b）并按照式（2）初始化蜂蜜源（Source）。

c）基于步骤b的簇头选择方案，把另外N-k个非簇头节点分配到k个簇中，使每个节点与簇头的距离之和最小。

d）用K-means方法进行簇头节点的更新，根据式（1）计算每个Source的适应度值：

e）根据2.2中所述的人工蜂群算法更新Source。

基于公开测试集，把基于人工蜂群算法的K-means聚类算法和传统K-means聚类算法进行对比，测试算法性能。“白酒质量”数据集的每个样本包含酸碱度、酒精度等11类指标，并带有分类标签，通过判断样本分类的正确度测试算法性能。进行5次独立重复试验，试验结果如表1所示。

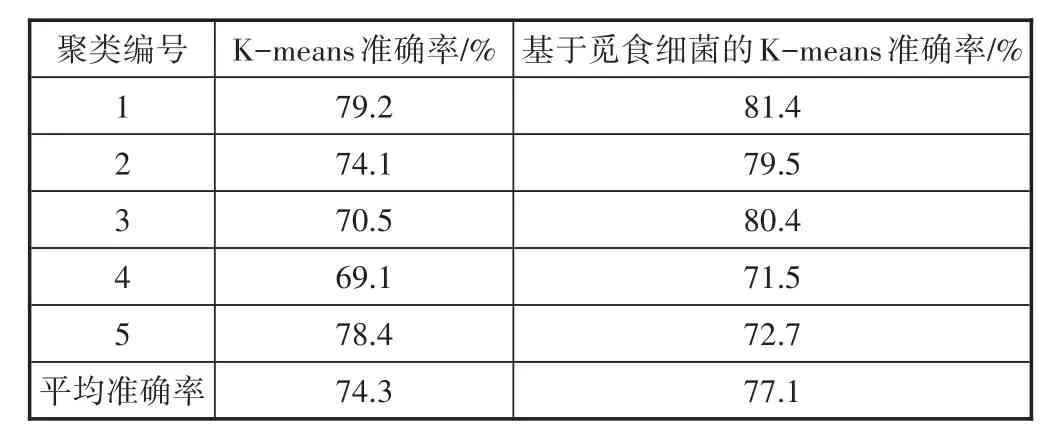
表1 2个算法聚类的准确性对比

由表1的结果可以看出，与传统的K-means算法相比，把人工蜂群算法引入K-means的簇头初始化过程，可以获得更好的聚类效果。

3 算法在信用卡精准营销中的应用

运营商大数据，特别是OSS域数据，详细刻画了用户的业务行为、时间位置、使用偏好、终端等信息，数据维度高，结构复杂，特征丰富，采用基于人工蜂群算法的K-means聚类模型进行分析，可以直观刻画出每个聚类特征以及影响意向率、转化率、核卡率的关键因素，为信用卡精准营销提供了有效支撑。

本文采用了某省2019年3月12日至2019年3月18日7天的XDR（X Detail Record）数据，筛选出10万用户，采用DPI（Deep packet Inspection）技术对数据进行解析入库，完成数据脱敏及预处理后，进行数据探索，方案如下。

3.1 数据探索

目前已经针对该10万用户进行了信用卡推荐，且已知其中完成了转化和核卡的用户ID。其中转化是指用户已经提交了办理该信用卡的申请；核卡是指用户提交了办理该信用卡的申请，且已通过银行审核，得到了该信用卡。首先，进行数据探索，为构建特征工程做准备。全体用户和转化用户的下行流量箱图如图1和图2所示。全体用户和转化用户的工作日日均话次如图3和图4所示。

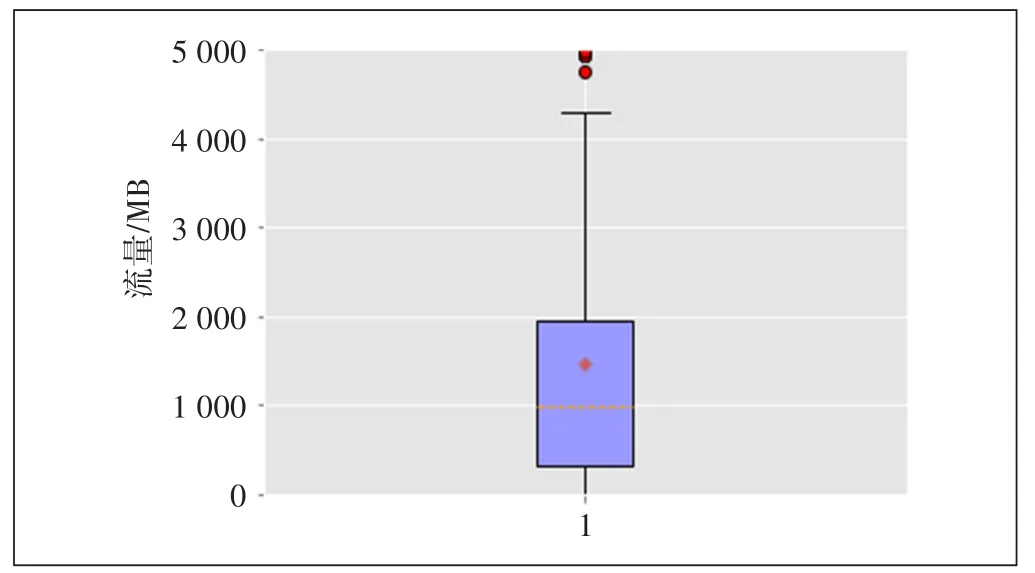
图1 转化用户的日均下行流量

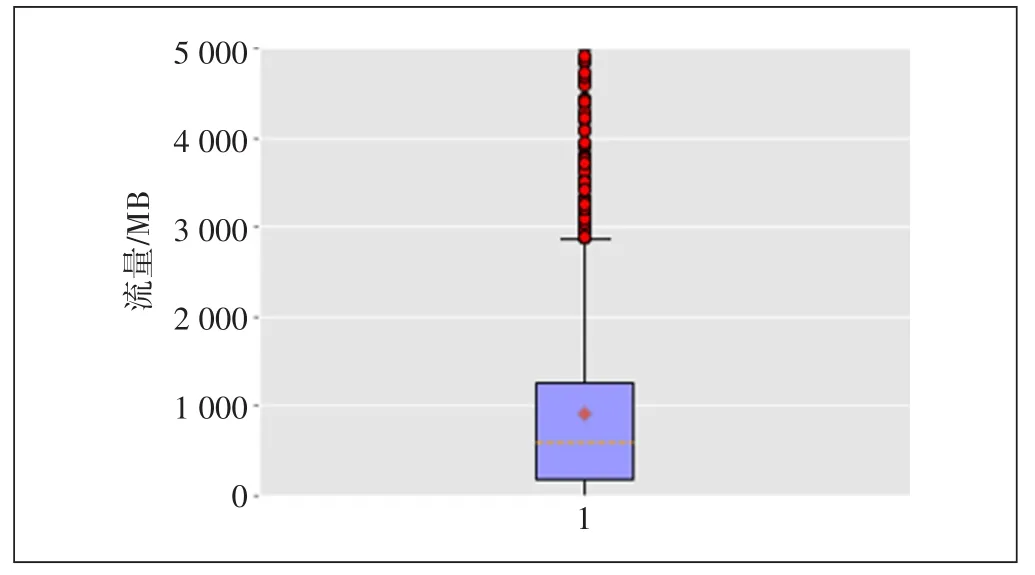
图2 全体用户的日均下行流量

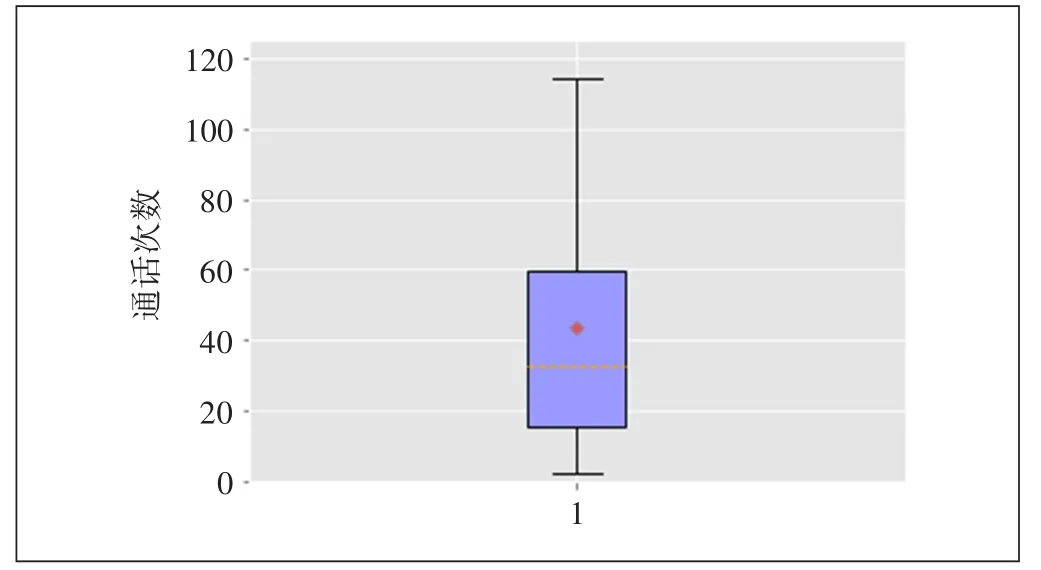
图3 转化用户的工作日日均话次

可见转化用户日均下行流量均值约为1 600 MB，中位数约为1 000 MB；全体用户的日均下行流量均值约为900 MB，中位数约为600 MB，存在一定差距；转化用户的7天话次均值为45次，中位数为33次，全体用户的7天话次均值为20次，中位数为9次，存在一定差距。

3.2 特征工程

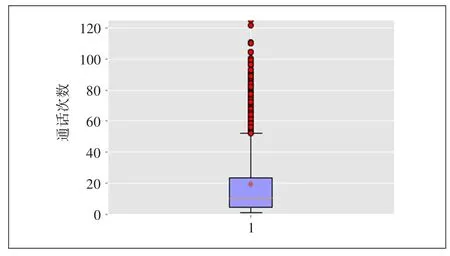
图4 全体用户的工作日日均话次

基于数据探索，整合7天XDR数据并关联工参，构建如表2所示的特征。

表2 聚类特征枚举

做如下设定：日间为8：00—19：00，夜间指19：00—次日8：00；根据DPI流量识别库对APP进行人工分类，各类别之间可以重复；为简化数据解析难度，假设用户每10 min访问同一个APP最多1次。采用等频分箱法对各个特征进行归一化处理，并删除异常值。

3.3 用户聚类

基于人工蜂群算法的K-means聚类模型对用户进行簇的划分，步骤如下：

a）初始化样本总数N=100 000，簇头个数k=7。

b）根据人工蜂群算法，设定参数gen=10，解空间个数100，解维度K=7以及最大迭代次数T=1 000，并初始化初始化P=100个蜂蜜源（Source），第i个解表示为：

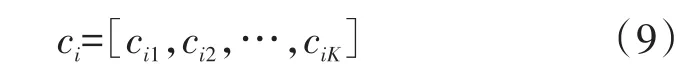
其中，向量ci中的元素cim为簇头，是一个h维向量，h为特征数据量，本文h=132；

c）基于步骤b）的簇头选择方案，把另外99 993个非簇头节点分配到7个簇，使节点与簇头的距离之和最小。

d）用K-means方法对簇头节点进行更新，计算每个Source的适应度值。

e）根据2.2中所述的人工蜂群算法更新Source。

f）迭代结束后，输出每一个簇的用户列表、聚类特征、转化率和核卡率。

3.4 结果分析

本案最终将100 000个用户基于132个特征分成7个聚类，由于篇幅限制，只在表3中标注每个聚类的意向率和核卡率，从中选择聚类中差异性较大的特征进行描述。

表3 聚类结果

从表3可以看出，聚类2和聚类6的转化率较高，达到6%以上；聚类7的核卡率较高，达到3‰以上。

聚类2、6、7的共同特征为日均流量和日均通话时长高于其他3个聚类，可见这3类用户的业务行为活跃水平高于平均值；7日使用年轻时尚APP个数/日使用全部APP个数、日均使用年轻时尚APP次数以及日均使用年轻时尚APP流量高于其他3个聚类（其中年轻时尚APP的列表包括今日头条、抖音、西瓜视频、小红书、快手等16种APP），表明聚类2、6、7对于年轻时尚类的APP有较高的使用率。

除此之外，每个聚类的自由特征如下。

聚类2的特征为：7日使用网贷类APP个数以及日均使用网贷类APP次数显著高于其他聚类（其中网贷APP包括人人贷、微粒贷、蚂蚁借呗、分期乐、快贷贷款、君融贷、闪电贷款、借点钱、宜人贷借款、拉卡拉、借了吗、惠借宝、借贷宝、拍拍贷借款等APP）；购物类APP的指标一定程度上高于其他聚类；工作日经过小区个数和休息日经过小区个数的比值较低。因此，可将聚类2概括为：有申请网贷的习惯，有较强的购物欲，可能没有较为固定的工作。

聚类6的特征为：日均使用银行及支付类APP次数显著高于其他聚类（特别是招商银行、京东金融、工商银行等APP），日均使用优惠促销类APP（拼多多、美团团购、薅羊毛、羊毛管家等）次数显著高于其他聚类，网贷类APP的指标一定程度上高于其他聚类，工作日经过小区个数较低而休息日经过小区个数较高，可能为价格敏感型用户，且在校学生比例可能较高（通过移动性指标得出）。

聚类7的特征为：网贷类APP指标较为显著地低于聚类2和聚类6，但是工作日经过小区个数/休息日经过小区个数指标较高，7日使用理财类APP个数以及7日使用理财类APP个数/7日使用全部APP个数较高（理财类APP包括pp理财、挖财宝、玖富钱包等），远高于其他聚类，同时办公类、股票及财经类、汽车类、家长类、家装类、旅行类APP指标略高于平均水平。聚类7的核卡率较高，该类用户具备和聚类2、6差别较大的特征：有一定的存款或资产，较大可能有较为正式的工作，且近期可能会有旅行、家装、购车等大额消费需求。

基于以上聚类结果，可以得到影响信用卡转化率和核卡率的关键性特征，从而更加有的放矢地进行信用卡精准营销。

4 总结

信用卡业务是银行零售业务利润贡献的重要组成部分，通过运营商大数据，可以对用户进行全面立体的刻画，进而分析信用卡潜在用户的特征。本文提出了基于人工蜂群算法的K-means聚类算法，可以提升K-means算法的簇头初始化水平，从而提升K-means算法性能。以信用卡精准营销为例，将该算法运用在信用卡精准营销场景中，可以获取影响意向率、核卡率的关键要素，从而更加有效地发掘潜在用户，未来该方法也可以运用到其他垂直领域，为行业发展带来新思路和新动能。