转子系统模态综合法
2019-09-27李文浩
李文浩
(哈尔滨电机厂有限责任公司,黑龙江哈尔滨 150040)
0 引言
结构系统动力分析通常采用整体结构有限元方法,可用于复杂的大型结构分析,例如蒸汽轮机,飞机,车辆,船舶等整体结构,但该方法计算规模大,计算时间长,所使用的磁盘空间和计算机系统太大。在有限元方法用于更高频率的振动分析时,需要将结构分为大量的单元,来得到详细的应力特性和位移。此时,模型里节点有数十万或是数百万个自由度,要直接解析这么大的结构模型是非常困难的[1]。即使可以进行分析,也需要花费大量时间并且效率极低。
模态综合方法是一种降低产生自由度的方法。此方法能够使大型模型简化变小,首先对每个子结构进行模态解析,再完成模态综合。因为只用了每个子结构的低阶模态,因此,大幅降低了整体模型结构的动力模型的自由度。并且,还能在不同机器上模态分析每个子结构,从而提升计算的速率[2]。
本文将着重论述常用于转子动力学中的模态综合方法。
1 模态综合法的基本思想理论和步骤
1.1 基本思想和理论
此方法的基本原理是根据其结构特征,将一个复杂的结构划分为多个子结构。再使用离散化方法对各个子结构进行多个力学解析。基于每个子结构的结点位移坐标,完成坐标变换和子结构进行分组。只需将每个子结构的模态坐标分组到整体结构坐标中,由子结构连接条件,执行第二坐标转换,从而清除非独立坐标,获得表示整个结构运动的广义坐标。这样,组集得到的模型的独立广义坐标的数量大大降低[2]。从而能得到整个系统的动力方程,此方程以独立的模态坐标表述。通过这种方式,求解低阶系统的动力学方程要容易得多[3]。由于大大降低了自由度,机器时间和存储器显著减少,传递矩阵法所需的机器时间较少,计算精度也非常令人满意。
子结构方法中最常用和最成熟的就是模态综合法,Raylei-Ritz方法,是动态子结构的理论基础。
1.2 模态综合法的基本步骤
模态综合法包括以下两个步骤[3]:
(1)基于每个子结构的结点位移坐标,完成坐标变换和子结构进行分组。
(2)由子结构连接条件,执行第二坐标转换,从而清除非独立坐标,获得表示整个结构运动的广义坐标。
模态综合方法遵循有限元方法,首先分析每个局部子结构,然后通过某种方法进行整体分析。通过每个子结构模态解析,获得一个“假设模态”,此“假设模态”可以根据一定的原则很好地表述整个模型结构的振动[4],然后使用假设模态分析法解析整个模型结构的振动。
假设某个简单的无阻尼自由振动结构,将原始的结构化为两个子结构α和β,各个子结构自由度包括界面自由度与内部自由度[5]。两个子结构的自由度,以矢量形式表述的物理坐标为
(1)
由力的对接条件和界面连续性条件,得
(2)
在简单叠加之后,获得整个结构的动能为
(3)
系统的总势能为
(4)
其中,[mα]、[mβ]和[kα]、[kβ]是质量矩阵与刚度矩阵,分别对应于α和β子结构的物理坐标{uα}和{uβ}。解析每个子结构的动力特征,选择合适的分支模态形成模态矩阵[φα]与[φβ],并对β和α子结构进行模态坐标变换可得
{uα}=[φα]{pα}
(5)
{uβ}=[φβ]{pβ}
(6)
其中,{pα}和{pβ}分别是两个子结构的模态坐标。子结构的自由度远大于分支模态数量。等式(5)和(6)通常被称为第一坐标变换,将等式(5)和(6)代入等式(3)和(4),由分支模态坐标表述的系统动能和势能即为
(7)
(8)
其中
[mα]=[φα]T[mα][φα],
[mβ]=[φβ]T[mβ][φβ]
(9)
[kα]=[φα]T[kα][φα],[kβ]=[φβ]T[kβ][φβ]
(10)
(11)
显然,因为存在等式(2)表示的条件约束,系统的模态坐标中,不是所有坐标都是独立的,因此由等式(7)、(8)表述的系统势能和动能表达式代入第二类拉格朗日方程,以获得结构系统运动方程[6]。仅在{p}去除了独立模态坐标时,才可以代入第二类拉格朗日方程中。
可以从每个分支的模态坐标变换方程(5)和(6)获得。
(12)
(13)
由此可得
(14)
(15)
由界面位移连续条件(2)式,可得
或写为
(16)
简记为
[C]{p}={0}
(17)

(18)
所以,等式(17)也可表述为

(19)
即得
{pd}=-[Cdd]-1[CdI]{pI}
(20)
所以有
(21)
[S]是独立坐标变换矩阵
(22)
上述公式(21)是第二坐标变换。所以独立广义坐标{q}={pI}可用于表述该结构的势能和动能
(23)
(24)
其中
[M]=[S]T[m][S]
(25)
[K]=[S]T[k][S]
(26)
因此,获得了无阻尼结构系统的自由振动方程
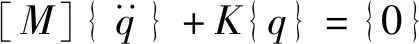
(27)
对应的系统广义特征值可表示如下
([K]-ω2[M]){A}={0}
(28)
这是综合每个子结构得到的新方程。等式阶数与每个分支结构模态的总和数减掉子结构连接坐标的数量相等。
普通的动力学方程,同样能够获得具有减小的自由度的等式方程

(29)
式中,由等式(27)得出[M],[K],其中[C]与{F(t)}可表示为
[C]=[S]T[c][S]
{F(t)}=[S]T{p}
(30)
为了描述空间结构的构造,即其运动和变形状态,通常使用两种类型的广义坐标:“物理坐标”和“模态坐标”。描述结构中每个点的几何位置坐标为物理坐标,是表述每个模态组件大小的坐标为模态坐标。这里使用术语“模态”而不是“振动类型”,因为“振动类型”是结构的变形形式作为主要振动。“模态”的概念是模式概念的概括,它不仅包含结构主振动的变形形式,它还包括由某些特定外力或关节位移产生的结构的静态变形形式。
转子动力学模态综合方法的基本思路和步骤基本相同,只是如何划分子系统,如何选择子系统的Ritz基础,如何处理综合中对接条件的发展,高效的模态综合技术是用很少的Ritz基来实现令人满意的精确度。子结构振动分析中,已发展出Ritz基选取的各种办法,如:约束子系统方法,自由子系统方法,组件假设形式方法。
2 总结
模态综合法有许多优点:
(1)显著节省计算机计算资源和时间,从而提升计算效率。
(2)此方法为子结构技术,能够计算超大的模型,同时,计算精度高。
(3)能够灵活的修改大系统中子系统设计。如果修改了子系统结构,则只需要重新计算修改后的子系统,再收集每个子系统。此过程中,不需要重新计算整个结构,降低了计算的时间。
因此,对于复杂大型结构,如:水轮机转子、船舶、汽车、飞机等结构,利用模态综合法分析结构,能够更好地解决计算速率和精度问题。
