陆基导弹的数学模型预算法设计*
2019-09-27王少纯王哲峰陈昱辰刘艳龙张馨丹
王少纯 王哲峰 陈昱辰 刘艳龙 张馨丹
(1.沈阳航空航天大学航空宇航学院 沈阳 110000)(2.沈阳大学环境工程学院 沈阳 110044)(3.沈阳航空航天大学航空发动机学院 沈阳 110000)
1 引言
随着我国国防力量的发展,弹道导弹已经成为捍卫祖国主权的战略力量。当导弹在飞行时,其质心在空间内会形成一条运动轨迹,这条轨迹就是通常所说的基准弹道,我们通过对弹道的分析研究可以提高导弹的性能和命中率。
因此在设计导弹时,要经过弹道分析掌握导弹的运动规律,进而选择正确的结构参数、选择合适的飞行弹道以及进行正确精准的弹道计算、进而评定导弹的基本性能参数、同时也能够为导弹的飞行试验提供需要的理论弹道参数数据。导弹弹道按照坐标系不同划分为绝对弹道和相对弹道。其中绝对弹道是建立在惯性坐标系中的导弹弹道模型。例如地空导弹、岸舰导弹、近程的地地导弹。本文通过对导弹飞行过程中位置参数和舰船运动时的位置参数进行分析,建立模型,确定导弹的轨道模型并解决相关问题。
2 导弹打击目标的具体分析
导弹的制导过程是一个复杂的过程,在这一过程中,可能会受到大气环境、攻击参数和对方反导系统拦截等很多条件的干扰。本文只考虑导弹本身轨迹的改变和攻击目标(航母)的运动以及地球的自转及曲率影响。
当目标为静止状态时,通过参数方程对三维空间内的弹道进行参数化分解,将导弹弹道这一复合的轨迹分解成为三个相互垂直的分运动。通过对三维位置点的分解,可以得到三个方向关于时间的速度参数方程,并代入地球自转[1],地主曲率和变轨技术等产生的影响因素,即可描绘导弹的弹道轨迹。
当目标具有一定运动速度,且运动方向与导弹三个分运动方向其中一个方向在同一直线上,因此只需要在弹道轨迹的基础上进行相关方向运动参数的修改即可。在此问题中,我们只需要考虑导弹第二阶段的飞行,即发射中段的导弹飞行模型即可达到跟踪的目的。以抛物线的顶点为起点,完善导弹中段的动态飞行模型与算法。
通过对导弹发射点和航母起始点在地球表面相对位置的确定,得到如下的相对位置图。
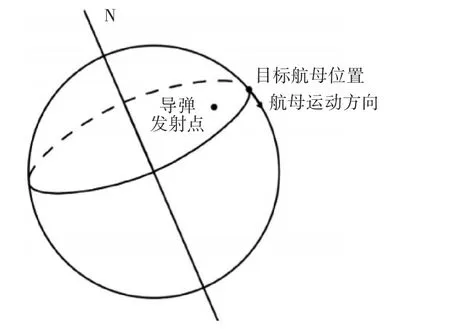
图1 导弹发射点与航母在地球上位置确定
通过二者的坐标和在途中的相对位置可以看出,在初始时刻,二者的维度不同。因此,即使航母不运动,导弹若命中目标,也需要跨越纬度飞行。同时导弹必须要向前飞行和向上方飞行以升高飞行高度。我们可以将导弹的飞行轨迹看成一个三维的曲线[2]。
对导弹的运动建立三维模型,将其运动轨迹分解为竖直(z)方向,东西(x)方向,南北(y)方向。
若从上空观测导弹的飞行轨迹,会发现如图2(a)中锁死的弹道轨迹,从某一纬度所在平面观测,会发现如图2(b)中所示的弹道轨迹。
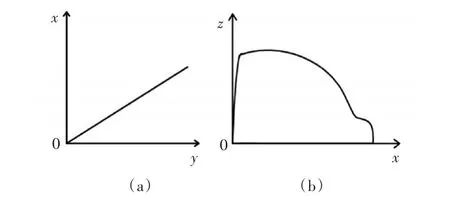
图2 不同角度的导弹弹道轨迹
导弹在发射后的运动轨迹可分为三部分[3],即发射段、中段和末段。如图3所示,导弹在发射段受重力和推进器产生的推力作用(空气阻力忽略不计)做抛物线式运动;在发射中段,导弹的运动可再分为两部分,一是只受重力和空气阻力作用的自由弹道,二是在卫星调控的基础上,受到重力和空气阻力共同作用的再入弹道;当航母进入导弹的打击范围,导弹进入末段轨迹,自主打击目标。
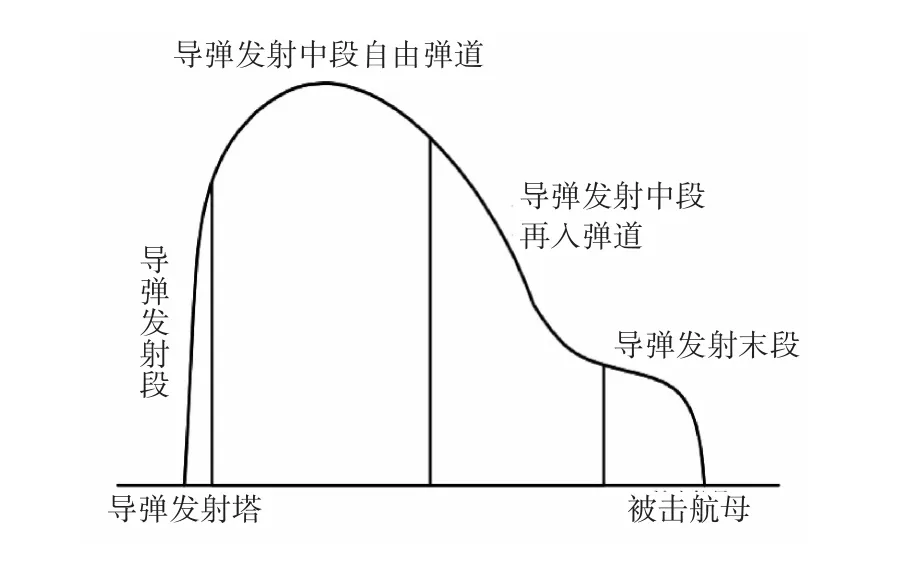
图3 导弹发射全程示意图
将导弹在x,y和z方向上的运动均看成为多次变加速运动的合运动,得到如下的运动方程。
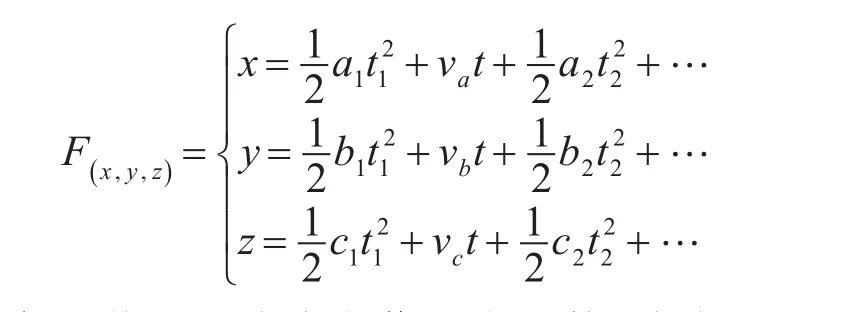
将导弹的运动分为若干个函数,式中的an,bn,cn等分别为导弹在第n段中x、y、z方向上的加速度,tn为导弹在第n段所经过的时间[4]。
以导弹发射车为坐标原点,xi为原点与地球的切线,方向指向正东方向,xi轴和zi轴相互垂直,方向竖直向上。导弹在发射段时,由于只受燃料推力,空气阻力和重力的作用,其轨迹可以简化为抛物线(y等于0)。在o-xizi坐标系内可以建立其弹道方程:
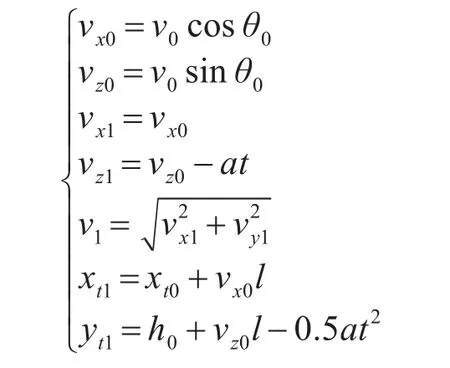
式中v0,h0分别为导弹发动机关机时的速度和高度,xt0为导弹在发动机关机时,在平面坐标系o-xizi上的横坐标,vx0,vz0分别为导弹发动机关机处,速度在坐标系上沿oxi轴和ozi轴上的分量,vx1,vz1和xt1,zt1分别为导弹于发射段时,在坐标系上的速度和位移分量,θ0为导弹发射段开始时的倾角(极小),t为导弹在发射段的运行的时间,a为导弹在上升时所受到的加速度矢量和,H为导弹飞行高度[5]。
在导弹的中段,导弹可分为自由弹道和再入弹道两个阶段,自由弹道是近似抛物线的运动轨迹,再入弹道为导弹从脱离抛物线到再一次进入到大气层后的运动轨迹。
导弹的自由弹道可以看成是导弹质心运动和绕心运动的结合。在中段,导弹的运动微分方程应由运动学方程,控制方程,质心运动方程和绕质心运动的动力学方程共同组成。我们同样以导弹发射车为坐标原点,研究导弹姿态运动方程[6]。
导弹质心运动方程可由动力学方程和质心运动方程积分求得:

导弹姿态方程可以利用导弹转动角速度ω1在坐标系的投影方程:
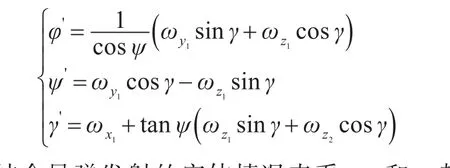
结合导弹发射的实体情况来看,ψ和γ都是很小的量,可以近似认为 sinψ≈ψ,sinγ≈γ,cosψ≈cosγ≈1。
与导弹进入自由弹道相比,导弹在进入再入弹道后所受的力主要为大气产生的阻力和导弹自身所受的重力。所以在以导弹发射车为坐标原点的三维坐标系中,可以建立再入弹道的微分方程:

式中:m为导弹去掉推进器后的弹头质量;vt为导弹质心在三维坐标系上速度的模;XF为空气阻力,并且:

式中ρ为空气密度;s为导弹横截面积Rb为导弹底部半径;d为导弹最大直径;vl为音速,v为导弹速度;i为弹性系数,该系数与导弹外形有关;为马赫数对应的标准阻力系数;F为阻力函数,另:
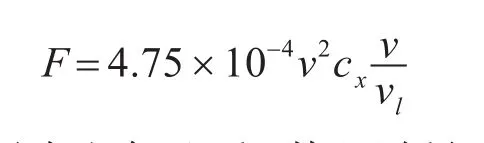
H为无因次空气比重,其跟随导弹高度变化的经验公式为
当高度小于9300m时:
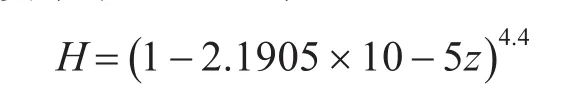
当高度大于等于9300m时:
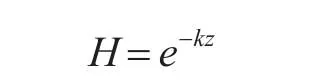
式中:k=0.0001。
在导弹中段的自由弹道结束后,导弹马上进入再入弹道,结合自由弹道和再入弹道,可以建立方程为
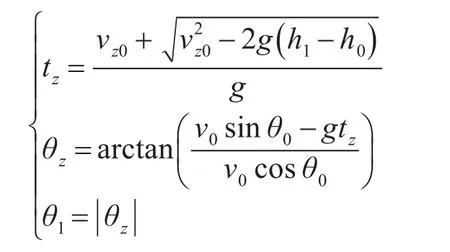
式中:h1为导弹结束自由弹道时的高度;θz为再入角;tz为导弹结束自由弹道时的时间,θ1为导弹进入再入弹道时的倾角。
考虑到在制导导弹的打击过程中,对方的反导系统会进行拦截,故找出有效的行进轨迹来对导弹进行变轨处理,来最大化降低拦截的可能性十分必要[7]。机动变轨技术是导弹在飞行中可随时改变其弹道,以躲避敌方反导防御系统拦截的一种突防技术,通常分为全弹道变轨和弹道中末段变轨两种。因为导弹发射初期是在己方国土内,所以敌人很难如此迅速的检测到发射信号,并且导弹在弹道末端是以二十秒内保持1000m/s的超音速进行俯冲,在这种高速短时状态下敌人很难精确对导弹进行拦截。因此,为节约发动机燃料和实现最高效的精确打击,我们将变轨技术只应用在中段。现阶段常用的变轨轨迹为蛇形机动和s形机动,其变轨原理均是有自带的小火箭在短时间内产生推力而完成。
变轨过程加速度是由推力T大小,方向单位向量uT和导弹的质量m决定的,即
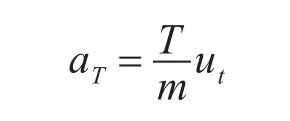
式中导弹的质量随燃料燃烧而减小,T可以表示为
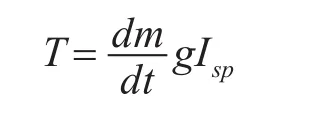
由上可得,推力方向也就是变轨方向是决定推力大小等参数的决定因素。所以我们研究出了基于大风级下的海浪波动模型。此模型通过模拟在大风级自然风下海浪的波形,来形成导弹的变轨轨迹。此轨迹具有随机性强,风级固定下稳定的特性,所以对最终打击精度不会有太大误差。我们将海浪高度在坐标系内的变化用一个三元函数来表示[8]:
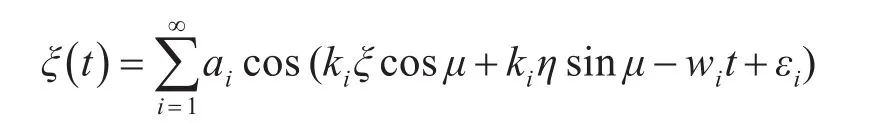
其中,ai,ki,wi,εi分别为第i次谐波的波幅,波数,角频率,初相位。
我们知道导弹变轨是由导弹携带的多个矢量火箭发动机,产生的脉冲推力来完成,在变轨过程中由于减少了前进方向的速度分量,会增加飞行时间。为了降低导弹负担,和避免贻误战机,并我们将海浪模型简化成二维问题。
这种“二元不规则波”可表示为
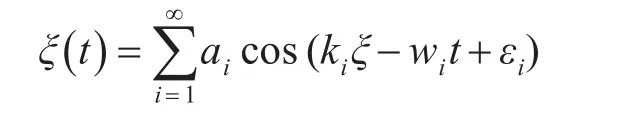
3 反导导弹杀伤区模型
从航空母舰发射的反导导弹的杀伤区是其不低于某一给定概率杀伤目标的空间范围,它主要是有反导系统的火控系统的参数决定,并且需要同时满足以下四个不等式。这表示出的区域就是反导系统的有效杀伤区。其中我们不考虑时间对相遇的影响[9]。
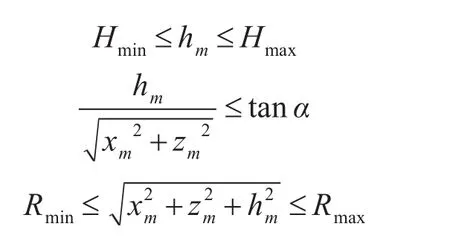
式中:Qm为OX与正北方向夹角。
我们可以把地球看成是一个绕地轴自西向东旋转的球体,由于它的旋转运动,地球表面上从两极到赤道上,各点的运动速度是随当量半径的增长而增大的。越靠近地球两端,表面的运动线速度越大,反之越小。而且,在同一维度上,海拔高度的不同也会导致线速度的偏差,比如说摩天大楼楼顶的线速度要大于底座的线速度。所以计算导弹轨迹时,如果不计算自转产生的影响,那么在导弹的长距离跨经纬度的飞行过程中,就会因为这两方面因素的影响,最终会导致无法精确打击目标。
这其中一个重要参数为偏近角E
平进点角:
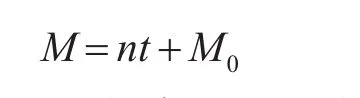
式中:M0=E0-esinE0相当于T=0时的平近点角。
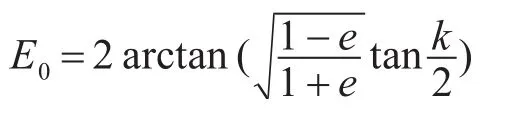
从开普勒方程可知,如果已知偏近点角E求M非常容易,但是在已知M的条件下求E,这是一个超越方程,用微分迭代比较容易求解。
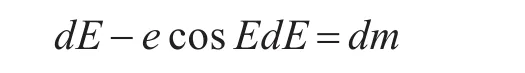
即
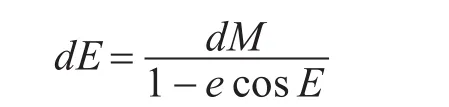
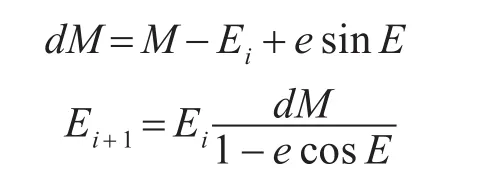
收敛条件:
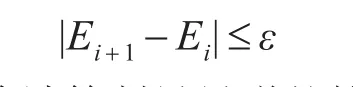
之后为精确计算制导导弹的轨道和打击点,我们在两个惯性参考系中,选择对发射段结束的分离点进行分析。A坐标系原点为地球质心,X,Y,Z轴满足右手法则且固定在地球上;B坐标系的X,Y,Z三轴的指向和A相同,但是它们随地球自转而旋转,即三轴的指向在不断变化。由上述两个坐标系的定义可得:1)在发射段结束时刻,A坐标系中导弹的位置矢量与B坐标系的导弹位置矢量相同[10],即:rKA=rKB,rKA和rKB的两个位置分量分别表示关机点经度和关机点纬度,K表示关机点。2)导弹在坐标系A,B中的速度不一样。速度矢量差为地球自转速度在该高度引起的牵连速度,用VKe来表示。导弹在A坐标系中的速度矢量VKA(Vx,Vy,Vz)为已知参数,则在B坐标系中的速度矢量VKB为
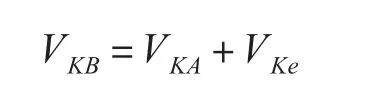
地球自转转向为自西向东,其角速度为w,所以,其引起的牵连速度VKe的方向沿K点自西向东,大小为ωrKcosΘk,这里Θk为K点纬度,rK为K点
赋初值:
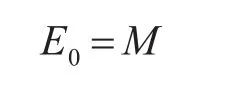
迭代公式:到地心的距离。
因此,考虑地球自转的导弹速度为
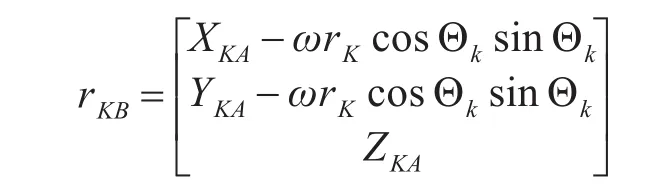
XK,YK,ZK是rKA的直角坐标形式。因此,当不考虑地球自转时,关机点的速度参数为rKA,rKA,而上述验证的考虑地球自转时的关机点参数为rKA,rKB。
如果把地球视为一个半径为6300km的球体,那么它的曲率不能忽略。
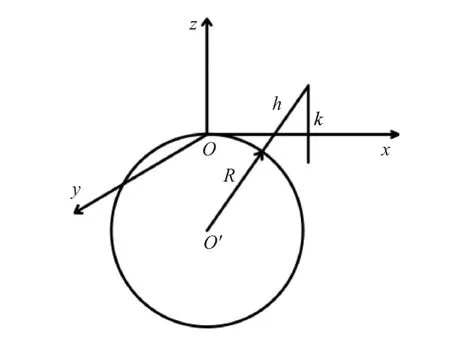
图4 地球曲率对导弹打击点的影响
不考虑地球曲率时,导弹平在飞段的弹道倾角θ≈0°,而实际上导弹存在弹道倾角θ':
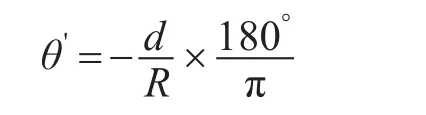
式中,d为导弹的飞行距离。
当导弹飞行340km时,θ'-θ=-3.09°,所以地球曲率对导弹打击点的影响不可忽略。

图5 俯仰角示意图
因为近程导弹的主轴不跟踪地球曲面[11],导弹发射时决定其运动状态,而且导弹的各方向角是以各向主轴作为基准测出的,所以导弹的各方向角的定义取决于以上所定义的坐标系。因为导弹发射时的水平面与主轴始终成一定角度,所以导弹的倾角始终是导弹发射时的水平面与弹轴的夹角(ϑ),而不是和所处位置水平面的夹角(ϑ'),如图3所示。所以只需假设原始坐标系是惯性参考系,根据导弹距离地表的高度(h)及其变化率(h')来模拟无线电高度表测得的导弹高度及其变化率,将其加入到导弹的高度控制回路中,并且把重力加速度改为g',建立考虑地球曲率的导弹弹道模型:

综上我们可以得出导弹打击模型为
通过对导弹运动的三维建模进行分析求解,我们已经得出了导弹打击静止点的运动方程。当航母向正南方向(y方向)以速度Vk匀速运动时,在上一个模型基础上,给导弹运动方程添加一个y方向的速度Vk即可得到问题二的模型[12]。
导弹质心运动方程可由动力学质心运动方程积分得:
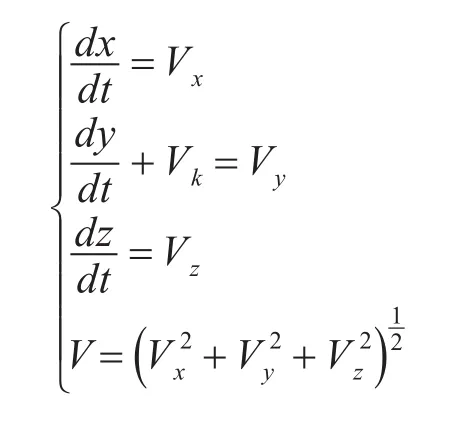
导弹姿态方程可以利用导弹转动角速度ω1在坐标系的投影方程:

与问题一相同,结合导弹发射的实体情况,ψ和γ都是很小的量,可以近似认为sinψ≈ψ,sinγ≈γ,cosψ≈cosγ≈1。
在目标移动时,导弹的中段自由弹道运动方程为
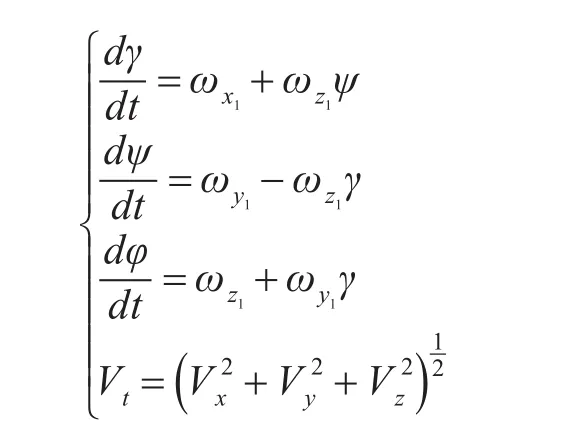
导弹进入再入段后,除y方向上加的匀速运动外,其运动方程和问题一相同,即:
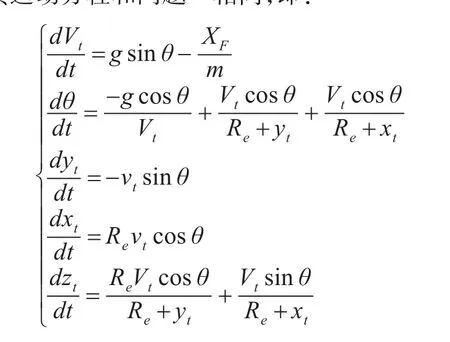

式中:m为导弹去掉推进器后的弹头质量;vt为导弹质心在三维坐标系上速度的模;XF为空气阻力,并且:式中ρ为空气密度;s为导弹横截面积Rb为导弹底部半径;d为导弹最大直径;vl为音速,v为导弹速度;i为弹性系数,该系数与导弹外形有关为马赫数对应的标准阻力系数;F为阻力函数,另:
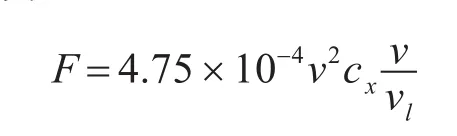
H为无因次空气比重,其大小跟随导弹高度变化的公式为
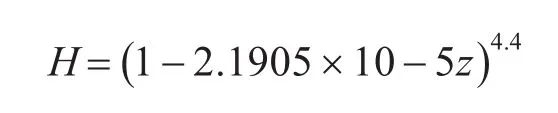
结合自由弹道和再入弹道,建立方程:
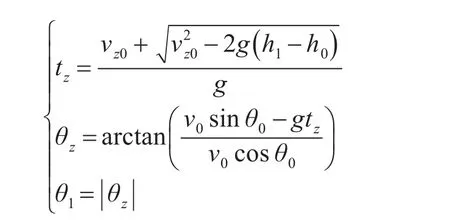
式中:h1为导弹结束自由弹道时的高度;θz为再入角;tz为导弹结束自由弹道时的时间,θ1为导弹进入再入弹道时的倾角
所以在目标航母以Vk的速度向南方向行驶时导弹的中段运动方程为
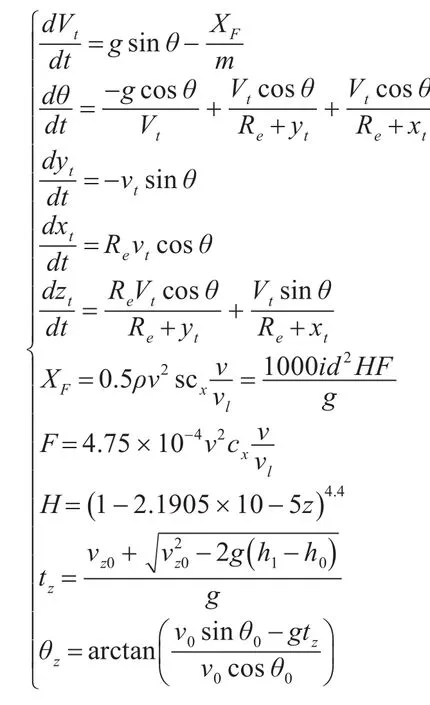
4 结语
该模型针对打击静止目标时的轨迹和打击静止目标时的轨迹均进行了数字化分析,并结合于公式,建立了全面的导弹打击和预防拦截模型,增加了精准率并减小了偏差。同时,考虑到到温度,天气,空气质量等对本模型的干扰,均将其设为干扰因子,计算比例后带入模型。
