改进神经网络的传感器故障诊断与容错处理*

温嘉斌, 赵红阳, 刘子宁, 包 汉

(哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080)

0 引 言

目前无刷直流电机(brushless DC motor,BLDCM)广泛应用于工业,航空航天等各个领域。无刷直流电机为获取位置信号需要安装位置传感器,来检测转子位置。考虑到传感器成本、体积等实际因素,无刷直流电机上使用最多的是霍尔传感器,然而当出现恶劣的环境条件如：高温、潮湿、外部震动、电磁干扰等均可能会对霍尔传感器产生很大的影响,在控制系统中,霍尔传感器的故障,将导致无刷直流电机工作异常,影响整个控制系统的稳定性。因此,霍尔传感器故障诊断及电机的容错运行已经成为电机调速领域的一个研究热点,国内外对此进行了大量相关的研究[1～6]。

人工神经网络是近几十年来得到迅速发展的一个前沿课题。由于其能够进行大规模并行处理,且具有高容错性、高自组织性、自适应性及逼近任意非线性函数的能力,其在突破现有瓶颈,更深入地探索和研究非线性现象时发挥了重要的作用。文献[7]设计了一种神经网络状态观测器,根据实际系统和神经网络观测器输出残差,从而对传感器故障进行诊断并确定容错控制系统。文献[8]提出一种基于神经网络的时间序列预测器的传感器故障诊断方法,先用神经网络对传感器输出序列建立预测模型,然后利用神经网络预测模型预测传感器输出值和传感器实际输出之差判断传感器是否发生故障。文献[9]提出一种混合粒子群优化(hybrid particle swarm optimization,HPSO)算法与神经网络相结合的传感器故障诊断的方法，利用HPSO算法对神经网络模型参数进行了优化,建立了预测模型,用于传感器故障诊断。但当训练样本过大,且要求精度较高时,人工神经网络还面临一些难题,传统反向传播(back propagation,BP)神经网络会有输出均方误差较大,诊断准确性较低的缺点。

本文设计了一种改进神经网络霍尔传感器故障诊断模型,并利用反电势法对传感器故障进行容错处理。最后通过仿真验证了整个控制系统的故障诊断能力,仿真结果表明,改进神经网络性能更好,输出误差绝对值低于传统神经网络输出误差绝对值,传感器故障诊断率高于传统方案。当传感器出现故障时,可实现电机容错运行,有效提高了系统的稳定性。

1 改进BP神经网络的故障诊断及容错策略

1.1 用于故障诊断的改进BP神经网络算法及拓扑结构

BP神经网络是一种多层前馈神经网络,该网络的特点是信号向前传播,误差反向传播。输入信号从输入层至隐含层,最后到达输出层。当输出与期望不匹配时,则进入反向传播,根据算法调节神经网络各层权值与阈值,最终得到期望输出[10]。

本文选择电磁转矩、相电压、相电流、电磁转速作为神经网络诊断霍尔传感器的故障特征。

为提高传统BP神经网络故障诊断准确率,本文设计了一种BP神经网络组合模型,将传统BP神经网络并行组合,给每个神经网络赋予相同初始权值,首先训练单个BP神经网络,每个BP神经网络有对应权重,后通过算法将单BP神经网络合并成多神经网络并行组合模型,再利用样本对组合模型进行反复训练,调整每个神经网络的初始权值,最终诊断结果由单BP神经网络输出函数加权得到。该算法详细过程如下：

1)提取故障数据作为每个BP神经网络的训练样本,设有b组训练数据,每组训练数据分布权值为1/b,对训练数据进行预处理,初始化神经网络的权值与阈值。

2)训练每个BP神经网络,用训练数据训练BP神经网络并预测训练输出,得到预测误差和E,误差和E计算公式为

(1)

3)计算权重并进行权重调整,根据误差和E计算序列权重w,权重计算公式为

(2)

(3)

式中g(i)为预测诊断输出,y(i)为期望诊断输出。

4)最后对单BP神经网络进行组合,设组合神经网络输出函数为z(x),每个神经网络输出函数为f(x)1,f(x)2,…,f(x)i。z(x)满足

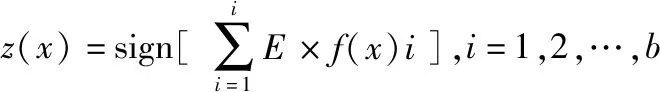
(4)

输出为神经网络诊断结果。整个算法流程如图1所示。

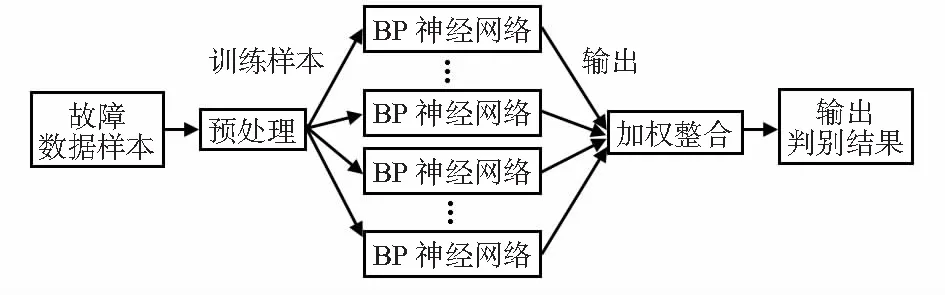
图1 改进神经网络算法流程

本文BP神经网络采用4×4×5的三层结构,输入层有4个神经元,对应上述传感器故障4种特征指标,输出层有一个神经元,当输出1代表传感器无故障,电机正常运行,输出-1是代表传感器出现故障。

改进神经网络模型由4个传统BP神经网络组成,其拓扑结构如图2所示,输入为训练样本,样本被送到4个BP神经网络中,4个传统BP神经网络输出加权得到改进神经网络故障诊断输出。

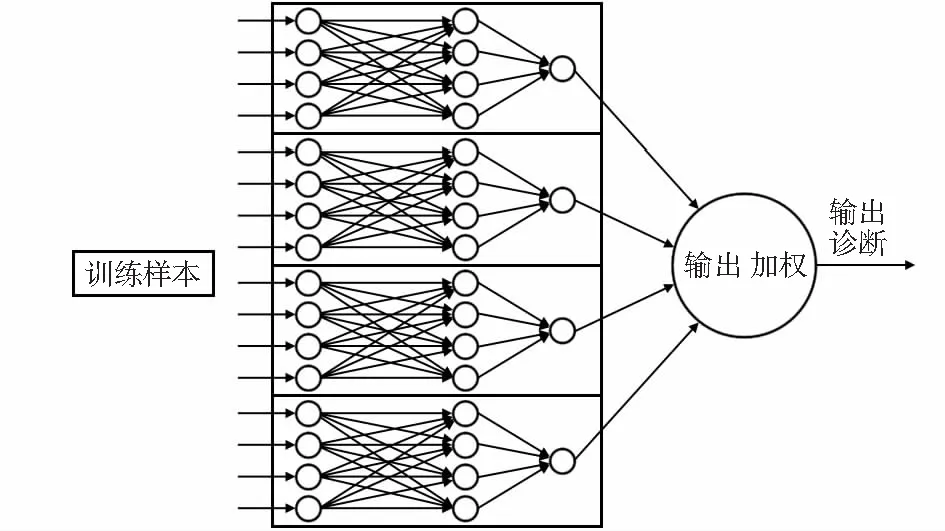
图2 改进神经网络结构

1.2 无刷直流电机传感器故障容错策略

在本文所设计的控制器中,采用了2套控制系统实现对电机的控制,其中,备用控制系统采用了无位置传感器系统来对电机进行容错控制。无位置传感器系统选择线反电动势过零法作为其容错控制方法。

为将有位置传感器故障系统顺利切换到无位置传感器的工作模式,本文设计了基于S函数的线反电动势过零点控制模块,具体模型如图3所示。S-F模块内有编写的S函数,在切换过程中可实现当前输出值与无位置传感器系统的输出值进行统一。在容错过程中只需要使用SIMULINK中的选择模块(Switch)便可以实现无刷直流电机从有位置传感器启动到无位置传感器的运行的顺利切换。

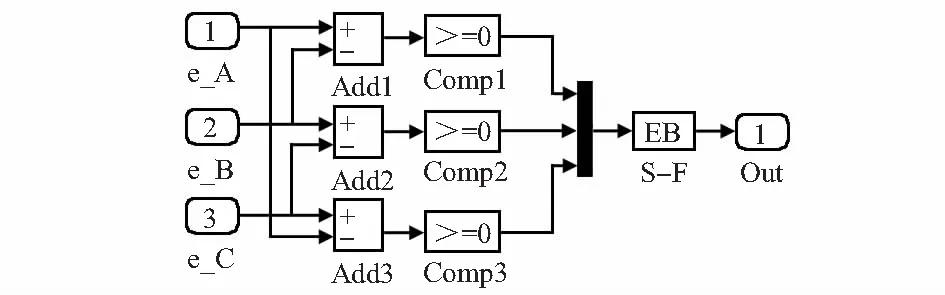
图3 线反电动势过零点模块

2 系统仿真分析

为验证本文所设计的无刷直流电机控制器的可行性,利用基于无刷直流电机的数学模型和MATLAB /SIMULINK搭建了无刷直流电机容错系统。在仿真中选用的无刷直流电机参数：Rs=1 Ω,LM=6.7 mH,转动惯量J=0.02 kg·m2,磁极对数为4,反电动势系数为Ke=0.048 V/rpm,阻尼系数B=0.000 2 N·m·s/rad。

在仿真中,本文在霍尔传感器信号中加入与、或门作为扰动信号,模拟信号丢失或其他故障情况。仿真中设0.2 s加入扰动,模拟霍尔传感器出现换相延迟及单个霍尔传感器故障,发生以上故障时无刷直流电机转速波形如图4所示,从图中可观察到,传感器出现故障及受到干扰时电机运行过程中均出现波动,电机不能平稳运行,单相传感器出现故障时电机在运行中相较另一种情况波动较大。

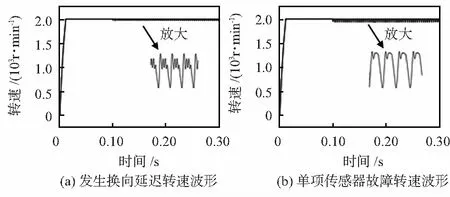
图4 霍尔传感器发生故障无刷直流电机转速波形

仿真后对故障特征参数进行数据提取,作为神经网络的训练样本数据,考虑到神经网络训练速度并节约功耗,单个样本的故障特征数据取故障发生后3 000个数值,以图4为例,选取0.2 s后的3 000个电流、电压、转速、转矩数据。从总故障样本空间中选择300组4×3 000训练样本,并分配权重,另取100组样本作为测试数据。通过训练,改进神经网络训练的均方差变化情况如图5(a)所示,在482次训练时达到稳定。

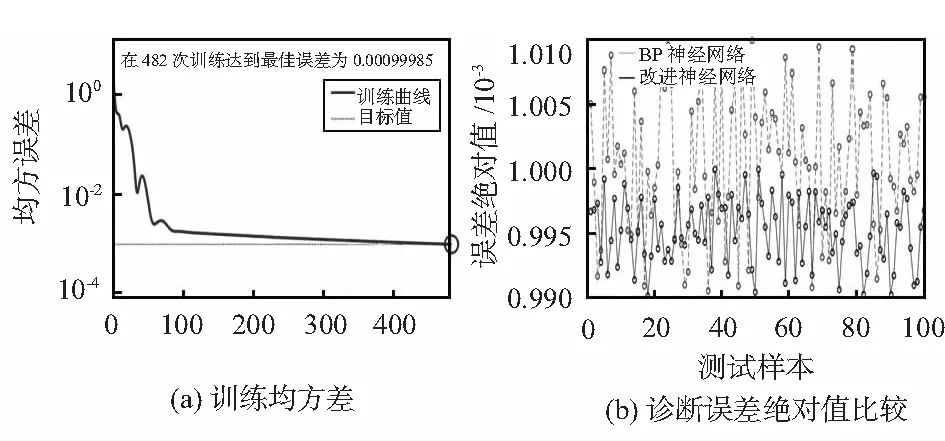
图5 神经网络训练均方差及诊断误差

图5(b)为改进神经网络与传统BP神经网络输出误差绝对值比较,可观察到改进神经网络输出误差明显低于传统BP神经网络误差。

取100组测试数据对神经网络进行检测,改进神经网络故障诊断准确率达到96 %,传统BP神经网络故障诊断准确率为91 %。

设0.3 s加入神经网络对故障进行诊断,针对换相延迟及传感器出现故障两种故障效果,无刷直流电机矫正后的转速波形如图6所示,从仿真结果可看出,采用容错控制的电机几乎无波动,与正常运行的电机性能基本保持不变,电机能够正常运行。

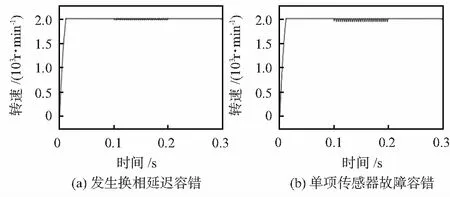
图6 霍尔传感器发生故障容错后无刷直流电机转速波形

通过仿真和实验验证可知：1)改进神经网络比传统BP神经网络具有更高的故障诊断率,性能更好。2)当不使用容错技术,霍尔传感器受到干扰或出现故障时,电机转速出现波动,不能平稳运行。3)改进神经网络检测到霍尔传感器故障后,控制系统切换至无位置传感器系统实现容错处理,对电机的转速波动有明显的纠正,电机能够实现平稳运行。

3 结束语

本文针对BP神经网络在样本数据量大,导致误差较大,准确率较低的问题,设计了一种改进神经网络模型,用于检测霍尔传感器故障,当检测出故障时,系统切换到无位置传感器系统对电机进行容错控制。经过仿真验证,改进神经网络与BP神经网络相比有更小的诊断误差,且故障诊断率可达到96 %。霍尔传感器出现故障时,控制系统可以保证无刷直流电机正常换相,电机实现较平稳运行。