机场客运接驳专线车辆营运优化

肖焕彬，初良勇,2*

(1.集美大学 航海学院，福建 厦门 361021；2.集美大学 现代物流研究中心，福建 厦门 361021)

0 引言

21世纪以来，在国家民航政策推动和航空市场自身不断扩充的合力作用下，我国机场数量逐步增加，各个机场间的竞争日趋激烈[1]。机场客运接驳专线是指以机场为中心，发往市内某个区域、周边城市等的一种接驳运输方式，以与机场交通配套合作为营运目的[2]。致力于打造以机场为中心，辐射周边的便捷、快速的机场地面客运接驳网络是各大机场客运接驳企业的长期发展目标。营运车型的合理配置是提升城市公共交通服务水平的重要内容[3]，机场客运接驳专线作为城市公共交通的重要组成部分，其营运方案和车辆配置方案不仅对机场乘客选择交通接驳工具有重要影响，而且与机场客运接驳专线企业的营运效率和财务收入密切相关。

国内外对公交车发车间隔的研究较多。Delle等[4]对不同公交运行方案进行分析，提出不同模式下的车辆调度优化方案；Palma等[5]通过考虑车辆数量、乘客延误费用以及不同期望出行次数，构建单线公交发车时刻优化模型；牛学勤等[6]以客流需求为基础数据，以乘客满意度和企业满意度加权平均最大为目标建立公交线路发车频率规划模型；邹迎等[7]以多条线路的区域调度为研究对象，建立以社会总体效益最优为目标的发车计划优化模型，提出“逐条配班，优化成网”的思想；覃运梅等[8]、Luhua等[9]根据公交调度优化的特点，以企业收益和乘客利益最大为目标建立公交发车间隔优化模型；Qian等[10]考虑乘客的车上时间成本、营运者成本，建立公交发车间隔的优化模型；陆婧等[11]考虑发车间隔和乘客人数的关系，对机场巴士发车时刻表进行优化；Parbo等[12]、Saharidis等[13]和Bruno等[14]研究乘客换乘的情况，以乘客换乘时间最短为目标对公交车的发车间隔优化进行研究。在车辆配置优化研究方面，国内外的研究相对较少。Jansson等[15]147-148提出采用车辆容量建立线性关系式a+bS(a为线路固定成本，b为线路变动成本，S为营运车辆容量)代表公交车的单位时间营运成本，进而求得最适合的车辆容量及发车间隔；祝付玲等[16]构建多车型的运力配置模型，但未定量研究车辆容量对发车间隔的影响；韩璧璘等[17]基于公交运输能力构建模型，对不同车型进行输送能力分析，最后得出营运车型的选择方案；李克聪等[18]对市内及城际客运营运的最佳车辆配备进行研究，提出最佳营运车队规模模型；Ruisanchez等[19]、Dell′olio等[20]、Ibeas等[21]以车辆营运成本和乘客等车成本之和最小为目标，建立营运车型优化模型，并设计相应算法进行求解；Ceder等[22-23]根据运力配置多目标方法，制定了多车型兼顾均衡载客量的发车计划。

上述研究中，较少考虑到营运中的实际车辆容量限制条件，而在实际营运中，选择满足容量需求的车型对公交服务水平和乘客满意度有重要影响。本文在考虑实际车辆容量限制下，单位时间内发车供给必须满足乘客需求的状况，构建相应的优化模型并进行求解，对机场客运接驳专线的营运车型选择和发车间隔进行优化。

1 问题描述与条件假设

1.1 问题描述

在某个机场的客运接驳专线中，营运总成本分为营运者成本和使用者成本，同时乘客需求随时间改变时，最佳车辆容量也随之改变，需要在某个特定约束下，安排车辆容量与乘客需求相匹配的车型及制定线路合理的发车间隔，满足乘客需求，在这个过程中使营运总成本达到最小。

1.2 假设条件

1)线路规划上只有2个端点(始点和终点)设站，即只有2个端点有乘客需求，符合大部分机场客运接驳2点专线的实际情况[24]。

2)目标函数不考虑购车成本。

3)发车间隔的制定必须考虑到每次发车皆能满足当时的最高需求。

4)不考虑线路营运中突发情况对模型的影响，默认线路的日客流量相对稳定。

2 车辆营运优化模型

2.1 模型构建

在机场客运接驳线路中，营运者成本和使用者成本随营运车辆容量(即车型大小)和发车间隔的变化而变化。本文在不考虑购车成本的条件下，以营运总成本最小为目标函数构建模型，求解满足单位时间内乘客需求的最佳车辆容量，并在车辆容量限制下求解最佳发车间隔。

1)营运者成本

营运者成本为车辆在单位时间内的营运总成本，其决定因素在于投入营运的车辆数

N=nT/h，

式中：T为线路单趟营运所需时间，h，T=D/v，其中D为车辆实际行驶的线路距离，km,v为车辆的平均速度，km/h；h为发车间隔，h;n为每次发车的数量，辆。

根据实际情况，大部分线路每次发车数量为1辆，即n=1辆,故营运者成本

Co=NB=DB/(vh),

式中：B为单位时间车辆的营运成本，元/辆。

2)使用者成本

使用者成本包括乘客等车时间成本与乘客车上时间成本。

当发车间隔在合理范围内，一般乘客会随机到达站点等车，在乘客到达站点的时刻随时间近似均匀分布的状况下，乘客平均等车时间近似为βh，β为等车时间系数，β=0.5，乘客等车时间成本

Cw=Quβh,

(1)

式中：Q为单程线路总需求，人/h；u为乘客等车时间费用，元/人。

乘客车上时间成本

Cv=Qwd/v,

式中：w为乘客车内时间价值，元/人；d为乘客平均乘车距离，km。

故使用者成本

Cu=Quβh+Qwd/v。

(2)

由于车辆单位时间营运成本与车辆容量(即车型)有关，故本文采用线性单位时间公交车营运成本函数B=a+bS求解最佳营运车辆容量S*[15]147-148。

此外，在实际营运当中，须考虑最小和最大发车间隔。最小发车间隔通常由投入营运的车辆数决定。最大发车间隔分为2个层面：一是公共交通政策所决定的间隔，主要是为维持一定公共交通服务水平所设定的发车间隔；二是在实际车辆容量限制下，单位时间内发车供给必须满足乘客需求的发车间隔。

为使乘客需求得到满足，最大发车间隔的制定必须考虑到每次发车皆能满足当时的最大需求，故本文侧重第二个层面。

为使线路的营运成本最小，根据式(1)(2)、文献[15]147-148及满足乘客需求的最大发车间隔限制条件，构建模型

minC=minCo+minCu，

s.t.
Co=D(a+bS)/vh，
Cu=0.5Quh+Qwd/v，
h≤S/G，

式中：G为最大单位时间乘客需求，人/h。

2.2 求解方法

将线路r以kmin(k=30，60，120，…)为单位分为m个时段t(t=1，2，3，…，m)，则线路r在所有时段t的总成本函数

Cr=Dr(a+bSr)/(vrthrt)+0.5Qrtuhrt+Qrtwdrt/vrt，

(3)

式中：Dr为线路r的实际距离，km；Sr为线路r的营运车辆容量，人/辆；vrt为线路r在t时段的车辆平均行驶速度，km/h；hrt为线路r在t时段的发车间隔，h；Qrt为线路r在t时段的总需求，人/h;drt为t时段在线路r上的乘客平均乘车距离，km。

同时，在营运线路的基本配车数量可以满足发车间隔的情况下，为了节省成本，营运车辆应尽量选取小型车辆[25]，故根据模型的约束条件，对应的发车间隔选取容量限制边界条件h=S/G，则线路r的营运总成本

(4)

式中：Gr为线路r上最大单位时间乘客需求，人/h。

1)最佳车辆容量

将式(4)的Cr′对Sr求一阶偏导数，令其为0并求得Sr*，再将Cr′对Sr求二阶偏导数，得：

(5)

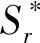
(6)

2)最小发车间隔

将式(6)代入式(3)，Cr对hrt求一阶偏导数，令其为0并求得Hrt，再将Cr对hrt求二阶偏导数，得：

∂2Cr/∂hrt2=2Dr(a+bSr*)/(vrthrt3)，

同理可知，Cr对hrt的二阶偏导数也为正值，故可证所求Hrt为总成本最小的发车间隔

根据容量限制约束条件h≤S/G，可知实际最佳发车间隔

(7)

3 算例分析

表1 2019-01—06厦门机场3条主要专线数据

厦门机场所有客运接驳专线中有厦门北站专线、曾厝垵专线和轮渡专线3条主要营运线路，营运时间为每天8:00—20:00，其在2019-01—06的营运数据如表1、2所示(表1、2中数据由元翔(厦门)空港快线有限公司提供)。

表2 2019-01—06厦门机场主要专线各时段平均需求量及平均行驶速度

表3 厦门机场3条主要专线在各个时段车辆的最佳发车间隔 min

目前，厦门机场北站专线及轮渡专线的营运车型为45座的宇通牌ZK6108客车，在不考虑购车成本的条件下，建议可替换成容量接近26座和27座的车型；曾厝垵专线的营运车型为33座的宇通牌ZK6842客车，建议可替换成容量接近21座的车型。此外，在满足乘客需求的条件下，通过对3条主要营运线路进行发车间隔的优化，相比原来固定的发车间隔和更多的日发车班次计划，可进一步控制营运成本，改善公交营运能力。

4 结语

本文在满足乘客需求的条件下，对机场客运接驳专线的营运车辆容量和发车间隔进行优化配置，降低了公交营运成本。可将多余的车辆投入新开发的专线或者客源潜力较大的专线，提升营运服务水平，进而提高对乘客的出行吸引力，这无疑会为客运企业及机场接驳运输带来益处。

提高机场客运接驳运输的营运效益，除了从车辆配置方面进行改进，亦可从以下途径进行优化：定期进行接驳运输市场的调查，以获取和掌握最新的市场动态资讯，从而做出相应的决策；结合运输市场需求推出不以机场为起始点的客运接驳专线，扩大自身产业在运输市场中的比例，降低对机场资源的依赖；对部分多余车辆进行客制化，尝试引入“定制巴士”模式，让一部分机场营运车辆根据乘客预先提出的需求自由选择行驶线路，以此吸收更多乘客，扩大市场占有率。