深部隧洞工程衬砌外水压力取值研究

陈 军，徐 江,2，罗代明,2，陈大松，刘其文

(1.贵州省水利水电勘测设计研究院,贵州 贵阳 550002；2.贵州省喀斯特地区水资源开发利用工程技术研究中心,贵州 贵阳 550002)

对于深部隧洞工程，天然地下水面线与隧洞轴线之间高差很大，形成了较高的外水头。对水工隧洞、公路与铁路隧洞而言，整个寿命周期既受到较大的地下水荷载作用，也会影响地下水赋存环境。地下水对隧洞的荷载作用是隧洞设计中的关键问题之一，在很多特定条件下，衬砌与围岩脱离，围岩中的渗透体积力不再对衬砌应力产生影响，衬砌成为承受外水压力的独立结构[1]，地下水对衬砌的作用按面力考虑，也即水岩分算[1- 3]，这是目前隧洞工程衬砌设计普遍采用的方法。

外水压力作为深部隧洞工程衬砌结构设计的关键参数，取值与外水头、隧洞防渗与排水方式等密切相关。隧洞工程对地下水的处理方式为全封堵、全排、堵排结合3种。全封堵方式由于需要承受同地下水头基本相当的水压力，因此不适宜深部隧洞工程；全排方式则容易造成地下水过渡排放、地面沉降及生态环境的破坏；堵排结合是围岩灌浆层与排水系统组成的地下水综合处理系统，在深部隧洞工程中得到了广泛应用，堵是控制地下水的排放量，排则是降低作用于衬砌的外水压力，二者不可或缺。

衬砌外水压力计算方法主要有3种：①折减系数法，SL 279—2016《水工隧洞设计规范》[4]采用折减系数法计算作用于衬砌的外水压力，是目前国内隧洞工程设计规范中唯一明确外水压力计算方法的标准，其本质是对静水压力的折减，折减系数与地下水活动状态、地下水对围岩稳定的影响相关[4]，因此需要根据隧洞开挖后揭露的地质条件才能进一步确定，前期设计时很难控制，除此以外，折减系数取值范围较大，设地下水位线至隧洞中心水头100m，若地下水影响符合SL 279—2016表C.0.2中的3级条件，则折减系数取0.25～0.6，对应外水压力为0.25～0.6MPa，具体取值难以把握，对受力较差的圆拱直墙断面隧洞，衬砌结构与配筋设计存在诸多不确定性；②解析法，П.У.Пοинматкин[2]曾就最简单的情况推导出各因素对称条件下渗透压力作用的弹性力学解(1972)，王秀英[5]基于堵排结合的地下水处理方式，根据地下水动力学理论[6]，推导了各向同性均匀连续介质、稳定流条件下圆形隧洞衬砌外缘、围岩灌浆层外缘的水压力以及隧洞排水量，针对外水压力计算的解析公式基本都是基于衬砌渗透排水而推导的，对于设置排水系统的隧洞，可以等效认为衬砌是透水的，并采用“等效渗透系数”来反应衬砌的下水排导特性[7]，但具体取值仍然是解析法求解外水压力的难点，不同的取值将得到不同的外水压力，在实际应用中困难重重；③有限元法，主要针对设置有排水孔的地下工程，比较典型的方法有杆单元法、排水子结构法、以管代孔、空气单元法、复合单元法等[8- 13]，排水子结构法排水子结构理论较严密，计算精度较高，但不足之处是需定义子结构与排水孔之间的关系，会显著增加数据准备的工作量和计算的复杂度，其他方法则是寻求宏观等效方法，避免对排水孔进行物理上的直接模拟，只要模拟出“排水效果”，其优点是不增加计算量，但受参数或模型“等效化”精度约束，计算精度不足。

依托贵州黔西北某隧洞工程，基于堵排结合的地下水处理方式，将深部隧洞工程地下渗流模型简化为轴对称问题，建立了含有排水系统的三维有限元模型，分析了衬砌的外水压力取值，得到了一些有益的结论，为类似工程今后的设计提供参考。

1 解析法求解衬砌外水压力

1.1 圆形隧洞轴对称解及适用性

山区深部隧洞工程，隧洞位置处的水深低于埋深，假定围岩为各向同性均匀连续介质，隧洞为圆形，衬砌内径为r0，外径为r1，远场稳定水头为r2为地下水头；地下水头很高设为H，水流为稳定流，其运动规律服从Darcy定理，同时假定隧洞的排水通过衬砌均匀渗水实现(认为隧洞工程排水孔流量均匀分布到衬砌中)，衬砌渗透系数k1，围岩灌浆层渗透系数kg，围岩渗透系数kr，可简化为轴对称问题进行处理，简化计算模型如图1所示。

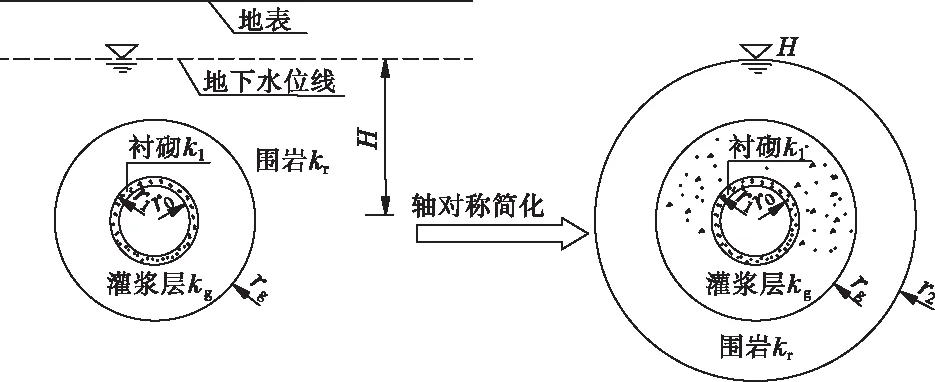
图1 圆形隧洞轴对称简化模型

由于衬砌厚度相对于地下水头较小，衬砌渗透力可以简化为作用在衬砌外缘的表面力，该表面力取该处的孔隙水压力[5,7]。根据地下水动力学理论[6]，推导出圆形隧洞的排水量Q和衬砌外水压力P1的计算公式[5,7,14]。

(1)

(2)

式中,h1—衬砌外缘处水头。

隧洞轴对称解不仅适用于圆形断面，同样适用于正方形断面、圆拱直墙断面、客专双线断面，只需要将非圆形断面按周长等效法换算成圆形隧洞尺寸即可[14,15]。除此以外，轴对称解也可用于浅埋隧洞水压计算[14]，但应注意求解得到的水压为隧洞中心处水压，对断面较高的隧洞应注意水压在高度方向的变化。

1.2 工程实例分析

贵州黔西北某隧洞工程长2.75km，最大埋深430m，最大作用水头79.6m(对隧洞中心)。由于采用圆拱直墙断面(断面尺寸12m×16.5m，顶拱中心角120°)，水荷载作用下衬砌的力学性能远差于圆形断面，因此，外水压力的取值对衬砌结构设计影响巨大。隧洞按周长等效原则换算为圆形断面后衬砌内径r0=8.46m，外径r1=9.26m，固结灌浆层厚度取6m,即r2=15.26m，远场稳定水头r2=H=79.6m，围岩渗透系数kr=1×10-6m/s(对应透水率5Lu)，考虑到一般固结灌浆技术水平取围岩灌浆层渗透系数kg=6×10-7m/s(对应透水率3Lu),隧洞设有排水系统，排水可以均匀排出，衬砌渗透系数为k1，设围岩渗透系数与衬砌渗透系数之比为n=kr/k1，利用式(1)—(2)可以分析隧洞衬砌渗透系数与排水量、衬砌外缘水头关系如图2—3所示。

图2 衬砌外缘水头与n的关系

图3 隧洞排水量与n的关系

由图2可知，衬砌渗透系数取值对外水头影响巨大。衬砌外缘水头随围岩渗透系数与衬砌渗透系数之比n增大而增大，也即衬砌渗透系数越小衬砌外水头越大；当n=5时，衬砌渗透系数为2×10-7m/s，衬砌外水头为12.25m，每延米隧洞排水量为14.72m3/d；当n=1000时，衬砌渗透系数为1×10-9m/s，衬砌外水头为77.47m，每延米隧洞排水量为0.47m3/d。

由图3可知，隧洞排水量随围岩渗透系数与衬砌渗透系数之比n增大而较小，也即衬砌渗透系数越小排水能力越差。同时，还可建立衬砌外水头与隧洞排水量的关系，如图4所示，显然，外水头随排水量的增大而线性减小，说明衬砌的透水性越好则衬砌的外水头越低，对应水压力也越小，相应要求隧洞排水性能越高。

图4 衬砌外水头与隧洞排水量的关系

根据式(1)，还可以计算出未衬砌前(毛洞状态，且未固结灌浆)的隧洞排水量为20.09m3/d。在上述讨论中，n的取值被限定在5～1000。若n→0，也即衬砌透水性能无限好，属全排方式，此时衬砌外水头近乎为0，排水量17.39m3/d低于毛洞排水量，说明围岩灌浆层能发挥堵水效应，若固结灌浆层渗透系数进一步减小则堵水效应更加明显，这里不再进一步展开。若隧洞未设排水系统或排水系统失效，也即隧洞采用全封闭不排水方式，根据GB 50108—2008《地下工程防水技术规范》[16]，对抗渗等级W8的衬砌混凝土而言，其渗透系数可取5×10-12m/s，则n=200000，计算得到衬砌外水头为79.59m，每延米隧洞排水量为0.002m3/d，近乎不透水，实际上当n≥1000时，排水性能极差，基本属于全封闭不排水方式，此时衬砌外水头近乎为全水头79.6m。式(2)还表明，只要围岩灌浆层渗透系数不为0，当衬砌采用全封闭不排水方式时，衬砌外水头即为全水头H，部分学者通过试验也证明了这一结论[7,14]。

由前述分析可知，衬砌外水头与隧洞排水量关系巨大。圆形隧洞轴对称解基于衬砌是透水的假定，而衬砌的透水是通过排水系统来实现，排水系统设计将决定衬砌渗透系数k1。由于不能准确获取衬砌渗透系数的具体数值，因此很难确定衬砌的外水压力具体数值，这也是目前采用解析法计算衬砌外水压力的困难。需借助有限元法才能准确求解排水系统条件下隧洞的外水压力。

2 有限元求解衬砌外水压力

排水孔是隧洞的主要排水工程措施之一，也是轴对称问题衬砌透水的计算假定，因此采用有限元法分析设置排水孔隧洞的衬砌外水压力。

2.1 计算假定与模型

2.1.1计算假定

从实用化角度对渗流计算假定如下[14]：隧洞围岩为均质、连续、各向同性介质；渗流为稳定流并服从Darcy定理；地下水位恒定，不因隧洞开挖、排水孔的排水而改变。

2.1.2计算模型

排水孔被用于改变渗流场，降低作用于隧洞衬砌的外水头，改善衬砌受力，因此作用于隧洞的外水压力将取决于有排水孔的隧洞渗流场分析。排水孔是人工设置在岩体中的圆形空心强导水通道，为渗流提供了一个相对开阔的空间，它对渗流的阻力远小于周边的裂隙和岩块，这就使得裂隙和岩块中的水流从排水孔孔壁渗出[11]，其原理与地下水向各向同性介质中水井的稳定运动相同[17]，因此将排水孔的孔壁作为溢出面边界，按给定水头边界条件处理。Gurehgian(1975)把排水孔作为计算域内给定水头的边界条件用有限元方法求解[8]，使用这一方法的困难在于排水孔的尺寸非常小(直径5～10cm)，远远小于计算域尺寸，而且隧洞排水孔众多，若将每一个排水孔作为内边界处理，将使网格过分复杂。

排水孔的横断面为圆形，其半径与巨大的渗流模型尺寸相比极小，可以采用等效矩形溢出边界代替圆形溢出边界，将空间曲面转换为平面以达到简化计算的目的，具体如图5所示。

图5 排水孔溢出边界等效为矩形溢出边界示意

计算域内渗流岩体按轴对称问题进行简化，也即模型呈圆环面状。由于隧洞衬砌多为防渗混凝土，因此渗透系数极小，近乎不透水，排水完全靠排水孔，因此模型不再考虑混凝土衬砌的作用，扩展为空间模型后由围岩灌浆层圆环岩体、远场圆环岩体组成，具体如图6所示。空间模型两端部为无排水孔溢出边界端部圆环体(体3)，无排水孔溢出边界端部圆环体(体3)之间由有排水孔溢出边界圆环体(体2)、无排水孔溢出边界圆环体(体1)交替连续排列组合而成。有排水孔溢出边界圆环体(体2)在洞轴线方向的长度为b，取排水孔周长为0.157m(孔径为5cm)；排水孔中心沿洞轴线方向的间距为L=2m，无排水孔溢出边界圆环体(体1)在洞轴线方向的长度为L-b；无排水孔溢出边界端部圆环体(体3)在洞轴线方向的长度为L/2-b/2，围岩渗透系数、围岩灌浆层渗透系数同前。具体建模时，纵向考虑布置5道排水孔断面，模型纵向长度与排水孔中心沿洞轴线方向的间距L有关，当L为2m时，模型纵向长10m，当L为3m时，则模型纵向长15m。

计算域圆环体外表面为给定水头H，排水孔为溢出边界，伸入岩体的长度为t，具体如图7所示，圆环体内表面(衬砌外表面)边界条件如图8所示，以不透水边界为主。

图6 圆环体隧洞排水孔三维渗流模型示意

图7 渗流模型边界条件示意

图8 模型内表面(衬砌外表面)边界条件展开示意

将计算域简化为轴对称问题并采用排水孔等效矩形溢出边界后，既能准确反映排水孔溢出边界的特性，又大幅降低了众多排水孔溢出边界三维隧洞渗流模型的建模难度，有效解决了网格复杂化的问题。除此以外，也有利于分析解析法中衬砌的等效参数；与常规的矩形水头边界相比，相同参数条件下圆形外水头边界渗流模型的来水量更大，因此对排水孔的排水能力要求也更高，得到的结果更加安全可靠。

2.1.3计算方法

渗流场与温度场在基本理论、微分方程、初始边界条件3个方面具有极大的相似性，因此可利用ANSYS热分析热传导模块来分析渗流问题[14,18]。

2.2 衬砌外缘水头特征

不同的径向排水孔布置方式，对衬砌外缘的剩余水头值的影响是不同的。当排水孔夹角为30°，也即断面均布12根，同时排水孔纵向间距为2m时，排水孔中心处的衬砌外缘水头特征如图9所示；当排水孔夹角为40°，也即断面均布9根，同时排水孔纵向间距为4m时，排水孔中心处的衬砌外缘水头特征如图10所示。

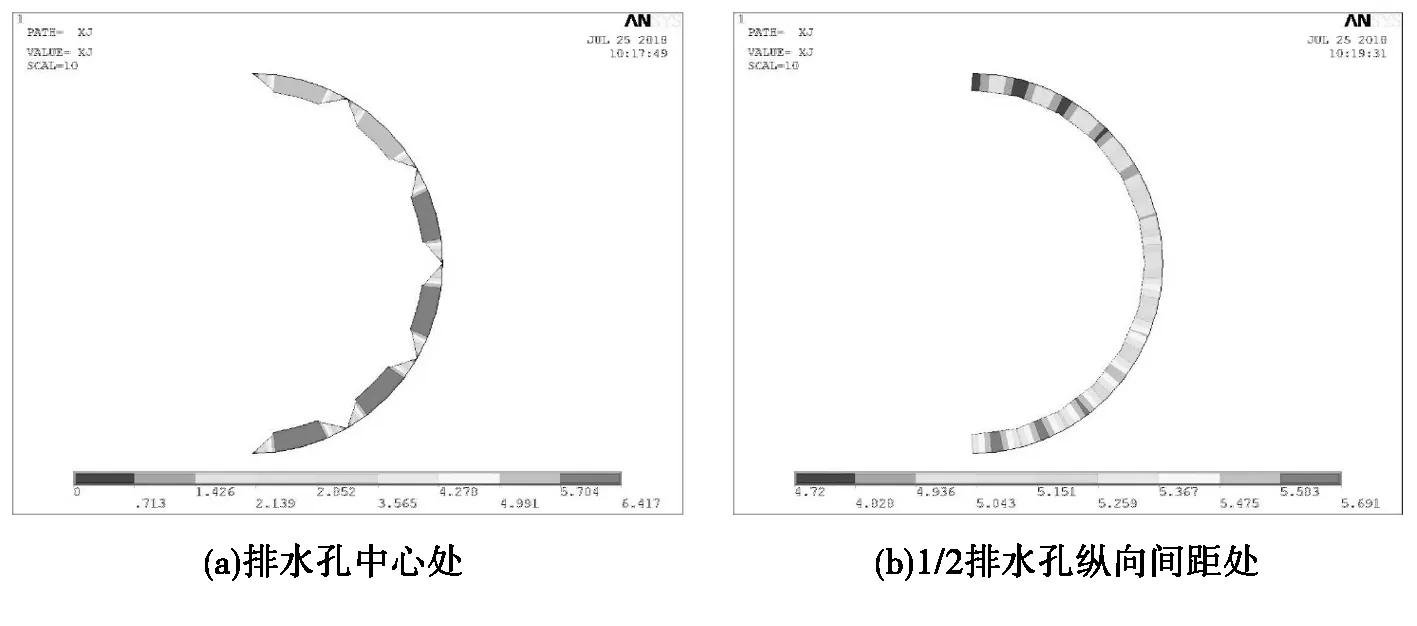
图9 衬砌外缘水头特征1(单位:m)

图10 衬砌外缘水头特征2(单位:m)

很显然，排水孔布置越密集衬砌外缘水头越低，最大作用水头并未出现在1/2排水孔纵向间距处断面，而是出现在排水孔中心处断面，位于相邻2根环向排水孔之间，图9方案的最大外水头为6.417m，图10方案的最大外水头为22.101m。为进一步分析作用水头，沿衬砌外缘对水头进行积分，可求解出图9方案排水孔中心处断面、1/2排水孔纵向间距处断面对圆心的平均水头分别为4.424m、5.716m，图10方案的分别为14.463m、18.083m。值的注意的是，衬砌外缘水头自拱顶至拱底逐步增大，但并不是按高差规律变化，以1/2排水孔纵向间距处断面为例，图9方案拱顶外水头4.72m，拱底5.691m，图10方案拱顶外水头15.253m，拱底20.901m；因此衬砌受力计算时应按外水头分布进行加载。

2.3 排水孔布置对衬砌外缘水头的影响

为进一步了解排水孔布置对衬砌外缘水头的影响，计算了排水孔夹角20°、30°、40°、60°、90°、以及排水孔纵向间距为2m、3m、4m时的情况。根据排水孔的夹角，可以计算出排水孔的环向间距，选择1/2排水孔纵向间距处断面作为特征水头断面，分别计算出对圆心的平均水头，可得到平均水头与排水孔环向间距的关系，如图11所示。

图11 衬砌外缘平均水头与排水孔环向间距关系

显然，作用于衬砌外水的平均水头随排水孔环向间距的增大而增大，随排水孔纵向间距的增大而增大。就本工程而言，排水孔的环向间距应控制在5m以内，纵向间距应控制在3m以内，此时作用于衬砌的外缘平均水头可控制在10m以内，将有效改善特大断面衬砌的受力。

采用有限元法计算得到未衬砌前(毛洞状态，且未固结灌浆)的隧洞排水量为20.29m3/d，是解析法计算结果的1.01倍，就工程应用而言具有较好的对比效果。同样，可得到排水量与排水孔环向间距的关系如图12所示。同样，可以得到衬砌外缘水头与排水量的关系如图13所示。

图12 隧洞排水量与排水孔环向间距关系

图13 衬砌外缘平均水头与排水量关系

显然，作用于衬砌外水的平均水头随排水孔环向间距的增大而减小，随排水孔纵向间距的增大而减小；作用于衬砌外缘的平均水头随排水量的增大而线性减小，不同的排水孔布置将决定系统的排水性能，排水孔布置越密集排水性能越好。

2.4 与解析法的对比

根据前述渗流计算成果，按照排水量相等的原则，根据式(1)可以计算出不同排水孔布置对应的衬砌等效渗透系数k1；按式(2)计算衬砌外缘水头。进一步将解析法计算结果与有限元法计算结果进行了对比，具体见表1。

表1中，衬砌外缘水头为对圆心的平均水头，有限元法计算得到的水头为排水孔中心处断面与1/2排水孔纵向间距处断面对圆心平均水头值的平均值作为特征水头。由表1可知，当衬砌等效渗透系数大于等于1×10-4m/s以后，也即k1/kr≥100，每延米隧洞排水量恒定为17.39m3/d，衬砌外缘水头近乎为0，衬砌相当于全排。因此，当采用有限元法计算得到的排水量≥17.39m3/d时，等效参数均按1×10-4m/s取值；事实上，解析法的溢出边界假定为衬砌内缘，衬砌外侧还存在一层围岩灌浆层圆环岩体，而有限元法的溢出边界为排水孔，排水孔则直接伸入了围岩灌浆层圆环岩体，由于溢出边界条件的变化必然导致排水量的差异。

表1 解析法与有限元法衬砌外缘水头对比

等效渗透系数随着排水孔环向夹角的增大而减小，排水能力也相应降低；但排水系统也不是越密集越好，当L=2m时，当夹角≤30°时，有限元计算得到的特征水头下降幅度不明显，而解析法计算得到的特征水头近乎为0。值的注意的是，采用解析法求解得到的排水量与有限元法相同，但衬砌外缘特征水头却小于有限元法，且排水孔布置越密集，这种差异越大，这同样是由于溢出边界的差异导致的。解析法中的溢出边界条件均匀连续，而排水孔的溢出边界间隔跳跃不连续，即使排水量相同，对水头的削减必然小于连续溢出边界，但是也更加真实可靠。因此，在采用解析法求解衬砌外水头时，需要进一步研究排水孔不连续溢出边界对水头计算公式的影响，提出相应的修正系数。

综上所述，当排水孔环向夹角采用20°，纵向间距3m时，衬砌外缘水头特征值为5.21m，将大幅改善深部隧洞工程圆拱直墙断面衬砌受力，经济性不言而喻。

3 结语

深部隧洞工程在地下水水位较高条件下采用堵排结合的地下水治理原则有利于隧洞本身的施工和运行，由于本工程所在地的地下水生态环境要求不高，因此按照常规的固结技术水平确定了相应的计算参数，采用圆形隧洞轴对称解分析了衬砌渗透系数对外水头、排水量的影响及关系。同时，采用有限元法分析了含有排水孔系统隧洞三维渗流场，得到了衬砌外缘水头特征值，并进一步研究了对应解析法中的衬砌等效渗透系数取值，发现了解析法与有限元法由于溢出边界的差异，即使排水量相同，计算得到的外水头将存在差异，需要进一步进行修正。尽管采用的有限元模型存在一定简化，但对深部隧洞工程衬砌外水压力的研究与应用具有广泛适用性。对于限量排放的隧洞，可以采用高压固结灌浆，并作进一步研究分析其外水头特征。