全球气候不同变化指标对流域暴雨洪水极值非一致性变化影响分析

孙 娟

(辽宁省河库管理服务中心(辽宁省水文局)，辽宁 沈阳 110003)

全球气候变化对水资源时空循环格局产生较大程度的影响，对暴雨洪水极值发生频率、时空分配特征以及强度特征产生不同程度影响，使得区域洪涝灾害的风险程度加重，对现有水利工程防洪安全产生不同程度的影响。当前气候变化对水资源序列非一致影响是水文学科亟待解决的难题和热点问题，也是人类社会对区域水资源保护以及水资源管理提出的研究需求。多个研究结果表明，不同气候变化指标对中国区域水资源影响较为显著。近些年来，GAMLSS模型可以对多个变量进行非线性变化分析，在分析气候变化对区域暴雨洪水影响的非一致研究中应用较为广泛，但在北方地区还未得到相关应用，为此本文结合GAMLSS模型，以辽河流域为例，结合GAMLSS模型定量分析4类全球气候变化指标对流域暴雨洪水极值非一致性变化的影响。研究成果对分析气候变化影响下辽河流域防洪安全、生态环境演变等具有重要参考价值。

1 GAMLSS模型原理

GAMLSS模型通过构建变量的概率密度函数f(yi)，并假定各个变量yi服从θi=(ui，σi，νi，τi)概率密度函数的分布，概率分布函数中的各个参数可以通过变量解译得到。在概率分布密度函数中μi，σi表示变量的大小变化以及时间变化的参数，而υi，τi则表示为变量分布函数的峰度及偏度。通过单调函数gk，可以表示出分布参数θk与解释变量Xk之间的关系：

(1)

也就是：

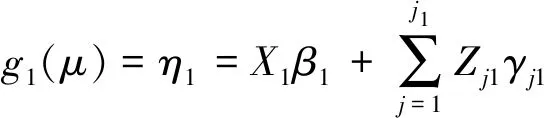
(2)

如果不考虑随机观测变量的参数分布影响，则可令jk=0，模型转换方程变为：

gk(θk)=ηk=Xkβk

(3)

若分析变量服从双参数变量的概率分布密度函数，则模型可转换成：

g1(μ)=X1β1g2(σ)=X2β2

(4)

通过假定变量分布与时间变化的尺度函数，建立其变化方程为：

(5)

将式(5)与式(4)结合，得到分布变量函数各参数与时间变化的函数方程。

g1(μt)=β11+β21t+……+βI11tI1-1g2(σt)=β12+β22t+……+βI22tI2-1

(6)

建立GAMLSS模型自回归变量的参数估计函数，函数方程为：

(7)

通过构建不同变量物理因子和参数变量之间的关系函数，可以对各参数进行解译。

(8)

通过试算方法对目标函数参数进行最优估计，得到不同参数的最优化估计值。

2 研究结果

2.1 站点概况

本文以辽河干流铁岭站为例，该站点位于辽河的中游，是辽河干流主要控制水文站点，该站点到辽河上游福德店水文站的河道长度为143km，流域区间的集水面积为13839km2，是铁岭站以上流域暴雨洪水主要区域，该区域主要分支河流为招苏台河、清河、柴河，福德店水文站以上流域主要为低山丘陵地区，海拔高度较低。而从福德店水文站到铁岭水文站这一区间主要为山地和丘陵的混合区域。海拔高度在200～900m之间。依据铁岭站1953—2018年实测洪水数据，结合GAMLSS模型，通过分析不同气候变化指标对辽河流域铁岭站暴雨洪水极值的影响。

2.2 模型最优拟合分布结果

结合GAMLSS模型对4类气候指标与暴雨径流两个变量的非一致关系进行分析。当变量累计概率密度函数参数未常量化，则认为其具有一致性变化(Model0)，当其参数变量随时间发生变化，则表示具有非一致性的变化(Model1)，而当参数变量随气候指数发生变化时，则表示为气候变化影响的非一致性变化模型(Model2)，在模型构建的时候，对各模型下与最大降雨和最大径流的拟合优度进行分析，结果见表1—2。

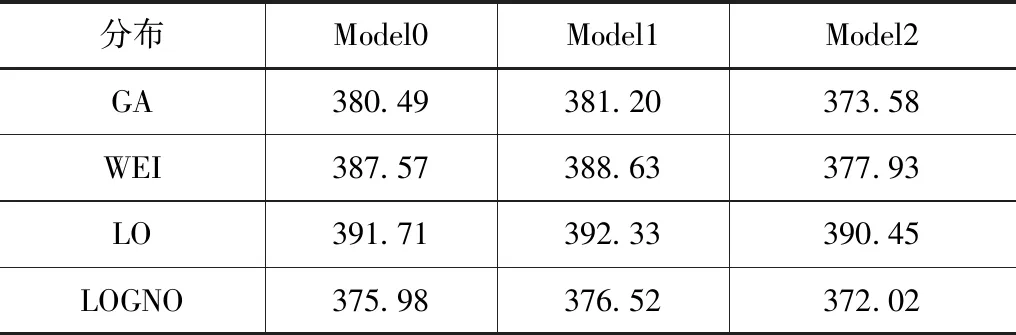
表1 年最大降雨量各模型AIC值

表2 年最大流量各模型AIC值

从表1—2中可看出，各模型的拟合优度AIC值变化不同，从总体变化结果可看出，对数分布下各模型与年最大降雨量和最大流量拟合程度最高，各模型下对数分布的AIC平均值最小。从表1—2中还可看出，三类模型下AIC的变化较为统一，均呈现逐步递减的变化趋势，表明各个模型下对数据系列的优化拟合程度逐步增加。考虑到时间和气候变化指标下各模型拟合结果较优，可看出气候变化对流域水文变量非一致的影响十分明显。

2.3 各类气候指标与暴雨洪水极值系列相关分析结果

在最优拟合分布分析的基础上，结合最优分布函数建立各气候指标与年最大降雨量及年最大流量之间的相关性，分析结果如图1所示。

图1 各气候指标与年最大降雨量级最大流量的散点图

从图1中可看出各类气候变化指标与年最大流量变化相关程度较低，这主要是因为流量受人类活动影响程度较大，如水利工程和下垫面变化对流量均产生较为明显的影响，因此使得年最大流量和各类气候变化指标的相关程度逐步减低，且与气候指标之间非线性变化较为复杂，非一致性变化较为突出。年最大降水量与各气候变化指标的相关程度明显高于年最大流量与气候变化指标的相关度，这主要是因为降水不受人类活动影响，其变化的主要成因主要来源于气候变化的影响，年最大降雨受到各类气候变化影响程度较大，年最大降雨量和各类气候变化指标之间的非线性影响程度较低，非一致现象不突出。

2.4 模型最优拟合分布参数函数分析

为对各模型最优分布下的函数参数进行优化分析，将年最大降雨和最大流量最优的拟合值和气候变化变量函数构建相关函数关系，从而确定各类气候变化指标与最大降雨与最大流量之间的非线性变化关系，分析结果见表3—4。

表3 年最大降雨序列和气候变化相关函数分析结果

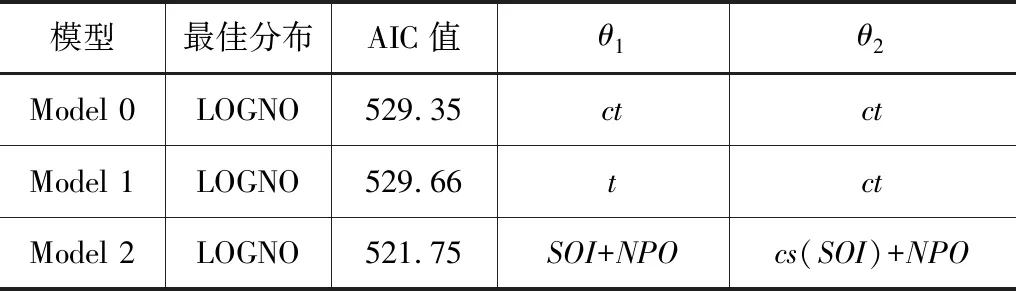
表4 年最大流量序列和气候变化相关函数分析结果

图2 各模型年最大降雨及流量量序列拟合残差分布图

从表3—4中可看出，年最大降雨和流量最大的分布参数θ1与南方涛动呈现较为明显的非线性变化，而与北极涛动呈现较为明显的线性变化，而另外一个参数θ2则与太平洋年代际振荡气候指标变化呈现明显的线性变化。分布参数θ1最佳协同分布变量为南方涛动和北极涛动两类气候变化指标，南方涛动及北极涛动时分布参数θ2的最佳协同分布变量。总体而言，北太平洋涛动对各区域最大降雨和流量分布参数的影响较小。由此可见，南方涛动、北极涛动、以及太平洋年代际振荡通过与最大降雨量和最大流量之间的线性及非线性变化关系进行影响转化，而太平洋年代际振荡则通过对线性变化关系对变量的方差产生较为明显的影响。基于Model 1和Model 2估计的5%、50%、95%分位数曲线如图2所示。从图2中可看出，Model 1模型下其占据最大流量比值为5%的序列呈现较为明显的递减变化趋势，而另外两个分位数递减变化较为不明显。加入不同气候变化指标后，Model 2在各变量序列中的曲线能够对其变化特征进行较为清晰的变化识别。可以看到，Model 2的5%分位数曲线突变十分剧烈，有几个明显的突变点，5%和50%分位数曲线变化不显著。这可能是因为气候因子的影响。

3 结语

暴雨洪水极值的最优分布为对数正态分布，该模型的AIC准则值最小，在区域年降雨径流极值序列拟合分析中可推荐使用。各气候变化指标中，暴雨洪水极值主要与SOI的非线性关系及NPO的线性关系，即SOI和NPO是分布参数θ1和分布参数θ2的最佳协变量。PDO和AO对分布参数的影响较小。

本文在气候变化指标对洪水影响分析中未能将人类活动影响进行分析，而最大流量受气候和人类活动的共同影响，在以后的研究中还应将人类活动影响进行分解后作为单一变量进行分析。