步进电动机细分驱动建模与运行曲线优化设计

瞿 敏,陈伟元 ,王 鹏

(1.苏州市职业大学 电子信息工程学院,苏州 215104； 2.江苏省光伏发电工程技术研究开发中心,苏州 215104)

0 引 言

步进电动机作为一种数字控制式伺服电机，匹配相应的电机驱动电路后，通过电脉冲信号改变电机励磁状态，使转子转动一定的角度。输入脉冲与电机位移之间存在着严格的同步对应关系，因此步进电动机具有定位精度高、无位置累计误差、响应速度快、可靠性高、易于控制等优点，并被广泛应用于自动化领域[1]。

驱动器性能与控制方法直接影响电机的运行性能与控制精度。步距角细分驱动技术的提出使电机步距角大大减小，提高了控制分辨率，步进电动机运行更加平稳、受控，有效改善电机低频运行时的振动问题[2]。另外，针对步进电动机起停过程中存在的失步、堵步和振动问题，电机运行速度曲线的设计与优化也成为研究热点。研究表明，在细分驱动的基础上结合恰当的升降速控制策略，能够进一步提高电机控制精度和系统稳定性，改善电机动态响应能力[3-4]。

本文以两相混合式步进电动机为研究对象，基于正弦电流细分和斩波恒流电机驱动方法,建立了电机开环控制系统仿真模型，实现了合成圆形旋转磁场下的电机恒等力矩步距细分驱动。并在细分驱动模型基础上进行电机升降速曲线仿真，提出了正弦加速度S曲线优化法，并对优化后的S运行曲线进行仿真验证。

1 电机控制系统建模

混合式步进电动机数学模型包含电气和机械两部分[5]。在假设电机磁路线性，且忽略相位之间互感的情况下，混合式步进电动机单相绕组电压与绕组电阻压降、转子位置变化、绕组电流变化相关，其中A相绕组的电压平衡方程：

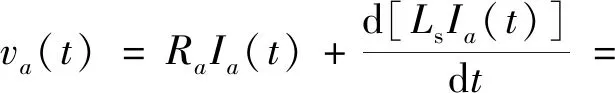
(1)

式中：Ls为A相自感，与转子位置角θ有关。

两相混合式步进电动机的矩角特性可视为单相励磁转矩的矢量和，是静转矩Tsm与偏转角度Δθ的函数：

Te=TA+TB=-Tsmsin(pΔθ)

(2)

在旋转运动下建立以电机轴为对象的机械运动方程：

(3)

式中：JL为机械负载的转动惯量；JM为电机转子的转动惯量；D为机械系统粘滞阻尼系数；TL为电机负载转矩。

综合电压平衡方程和机械运动方程，可以得到混合式步进电动机的仿真模型[6]。

在MATLAB/Simulink开发环境下搭建两相混合式步进电动机控制系统模型如图1所示。控制模型主要包含驱动模块、电流控制模块、升降速曲线生成模块和参数设置模块。

图1 电机控制模型

驱动模块由功率管构成两个H桥电路，分别实现电机A相与B相绕组电流功率驱动，并由电流反馈与比较电路实现相电流的斩波恒流控制。

依据步进电动机恒转矩细分原则，当步进电动机两相绕组采用相位相差90°、幅值按正弦规律变化的电流作为驱动电流时，电机内部合成恒幅均匀的定子旋转磁场，从而实现恒转矩幅值控制。此时电机A，B相绕组电流满足：

(4)

式中：Im为电流矢量幅度；n为细分数；s为在确定细分数后电机转动设定角度所需的步数。

使用Simulink中的S函数设计正弦电流细分控制模块，为两相绕组提供幅值、频率和细分数可调的阶梯正、余弦电流。当电流控制模块输出幅值为2 A、4细分时相电流如图2所示。控制模型理论细分数可以任意配置，但受到仿真步长约束，当系统仿真步长为10-6s时，电机细分数可在1 000范围内设置。实际在满足控制系统要求情况下，依据电机运行转速适当提高细分数，增大步距分辨率，可以提高电机运行稳定性与控制精度。

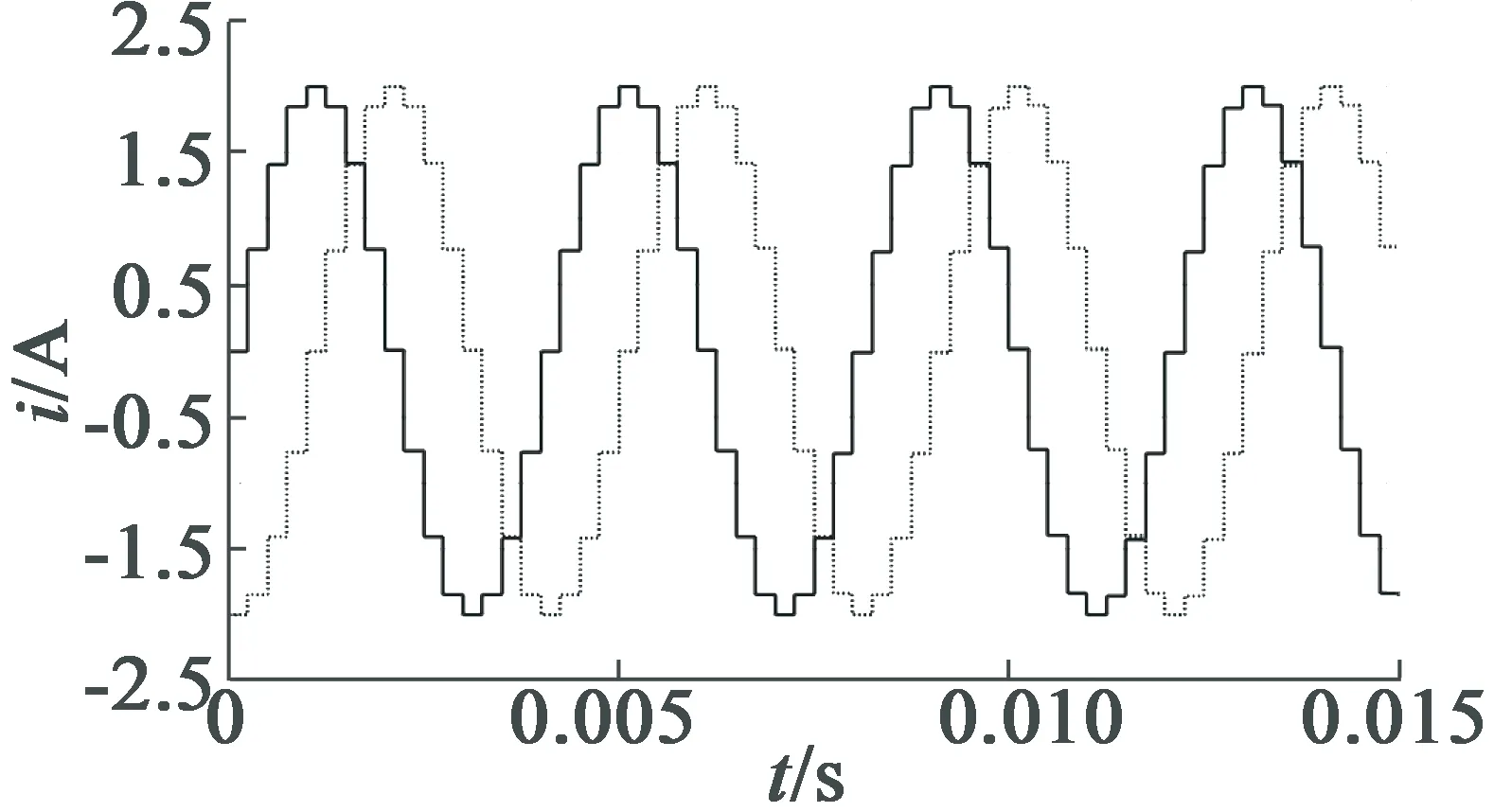
图2 4细分电机相电流仿真波形

2 传统升降速曲线分析

步进电动机直接起停时电机转速和加速度存在较大突变，加上转子惯性作用，往往导致电机失步、过冲、振动等问题。合理的电机升降速曲线设计有助于电机快速平稳运行。常见升降速方案有梯形、抛物线和S形[7]，如图3所示。

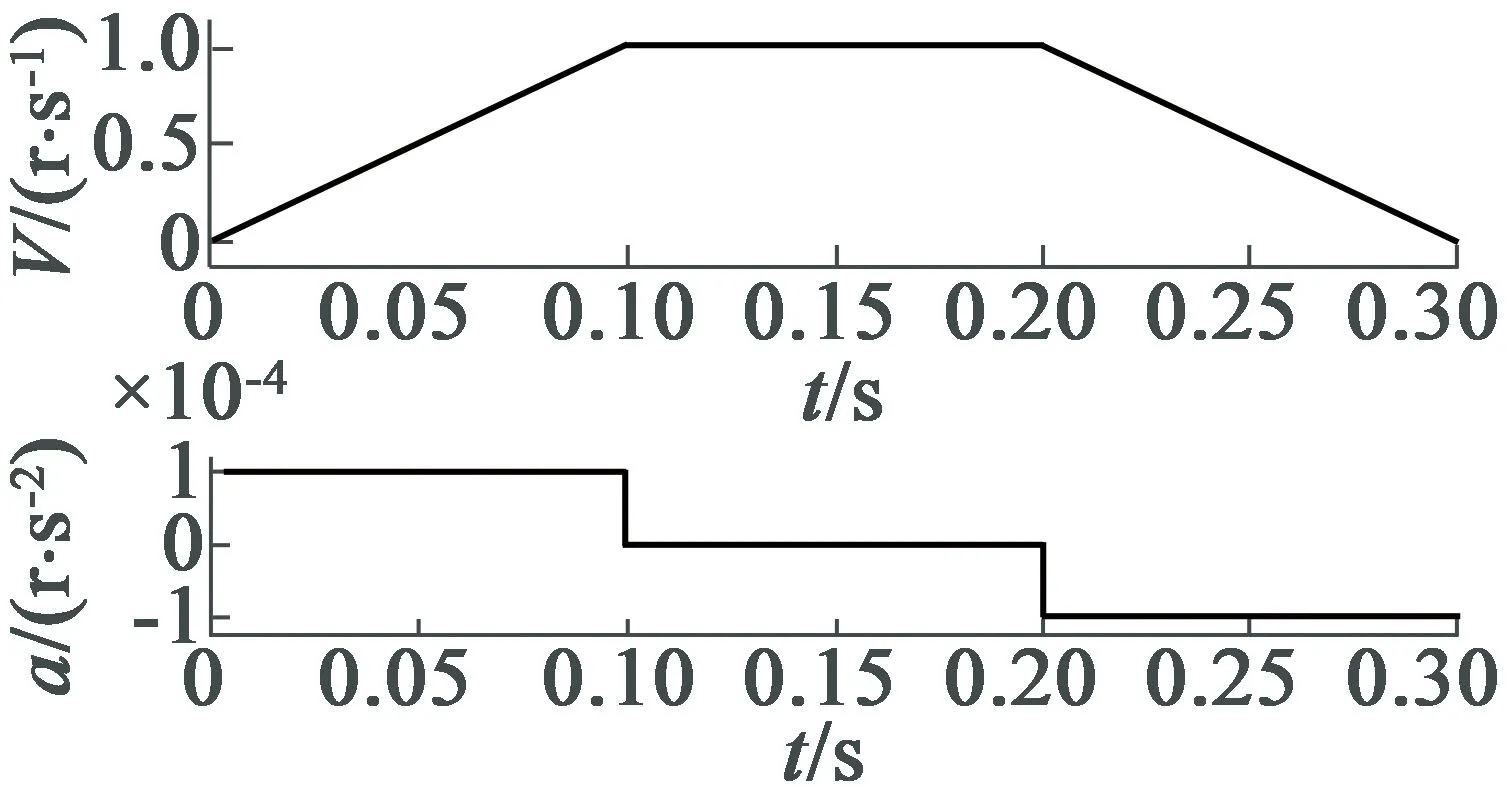
(a) 梯形

(b) 抛物线形

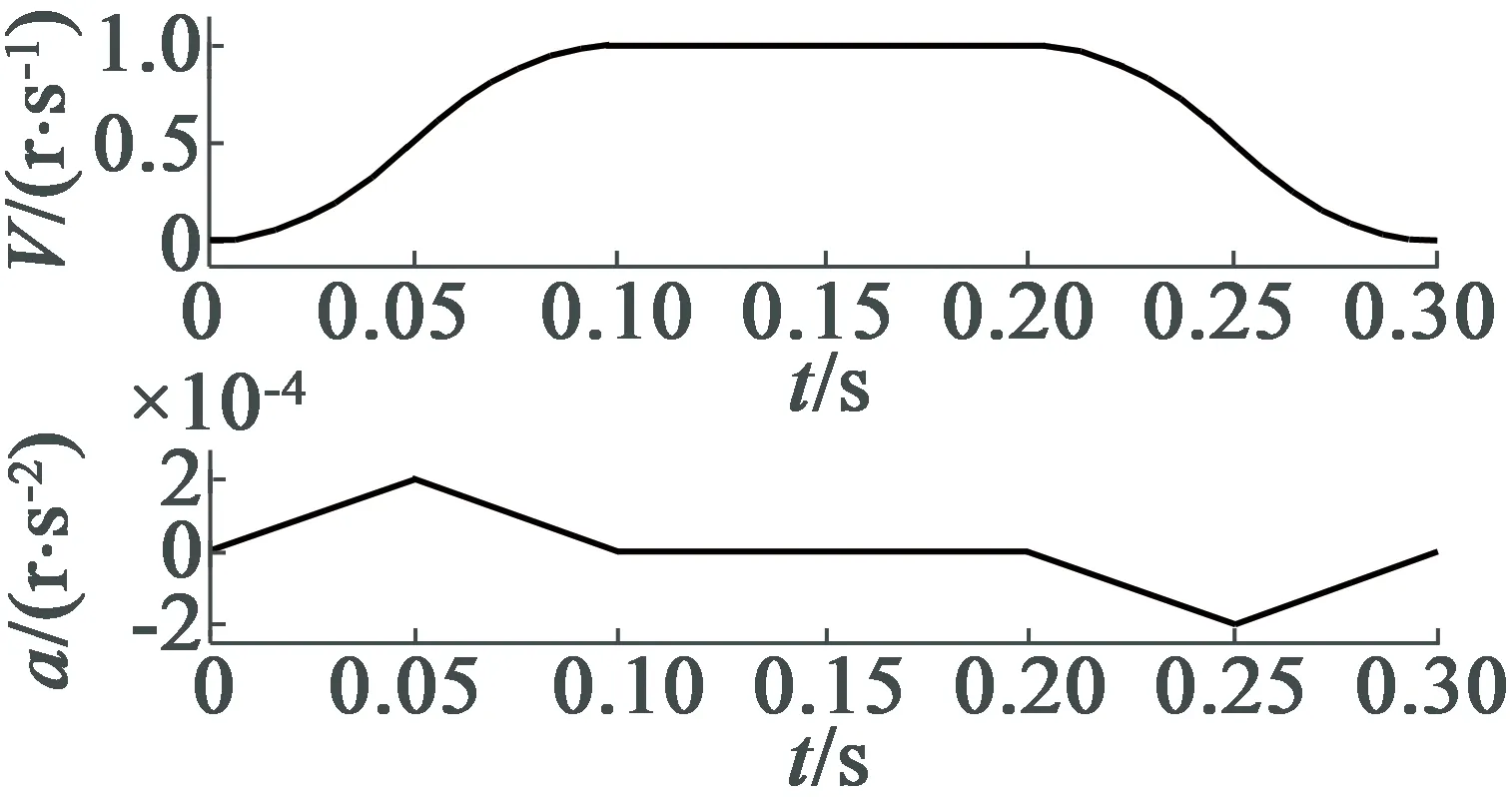
(c) S曲线形

梯形速度曲线在加速和减速阶段速度线性变化，加速度恒定，如图3(a)所示。其算法实现简单、效率高、响应快，但速度曲线过渡过程不够平滑，曲线分段衔接处加速度存在阶跃，会对电机带来柔性冲击。

图3(b)中电机加速和减速阶段速度按照抛物线规律变化，速度曲线相对平滑，电机升速快，但在起点和终点加速度大。起步时电机静态惯量比较大，须以较小的起动频率进行升频。在停止时，为了避免过冲，应该以较小的加速度实现降频[8]。抛物线法对电机存在一定柔性冲击，适合对升降速率要求较高的场合。

S曲线法因电机在加减速过程速度曲线呈“S”形而命名，其实现方法不固定，主要以加速度不产生突变为核心思想，达到电机快速平稳运转的目的[9-10]。传统5段S曲线法将电机的运行过程分成加加速—减加速—匀速—加减速—减减速5个阶段，如图3(c)所示。其中升速阶段的S曲线由两段抛物线构成加加速和减加速。S曲线法的速度平滑性好、运动精度高，加减速在任何一点的加速度都是连续变化不产生突变，但不够平滑，能在一定程度上避免柔性冲击。由于其涉及阶段较多，故实现过程较复杂。

3 正弦加速度S曲线优化

3.1 速度曲线设计

为了进一步改善5段S曲线的加速度平滑特性，采用正弦函数对加速度曲线进行优化。

设计电机加速阶段加速度曲线函数：

式中：Ton为电机起动时间。当常数A=10，加速时间Ton=0.1 s时得到正弦加速度曲线如图4(a)所示。

对式(5)的速度函数在[0,Ton]范围内进行积分,得到速度函数：

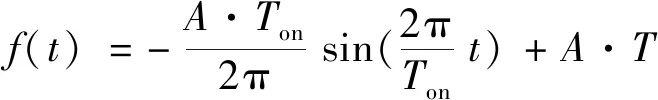
(6)

归一化后改进S速度曲线如图4(b)所示。

(a) 加速度曲线

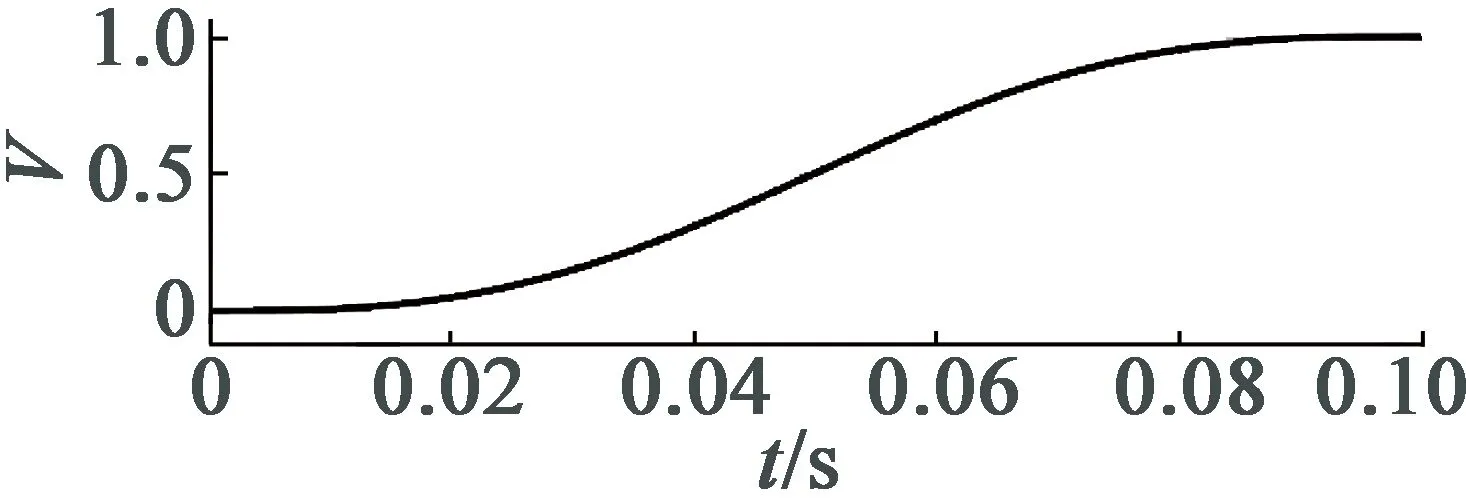
(b) 速度曲线

对正弦加速度积分,生成的速度曲线呈S形，也由加加速—减加速2个阶段构成，曲线连续光滑。加速度与加加速度均为正弦函数，具有连续可导特性，能有效抑制运行过程中的高次谐波。

对于完整电机运转过程，电机匀速阶段加速度恒定为0；减速阶段加速度与加速过程相反，加速度曲线位于Y轴负半轴。对整个加速度曲线进行积分，获得电机完整运行过程速度曲线，如图5所示。整个电机运行过程中速度与加速度曲线均平滑过度，无突变、无拐点，对电机柔性冲击小。

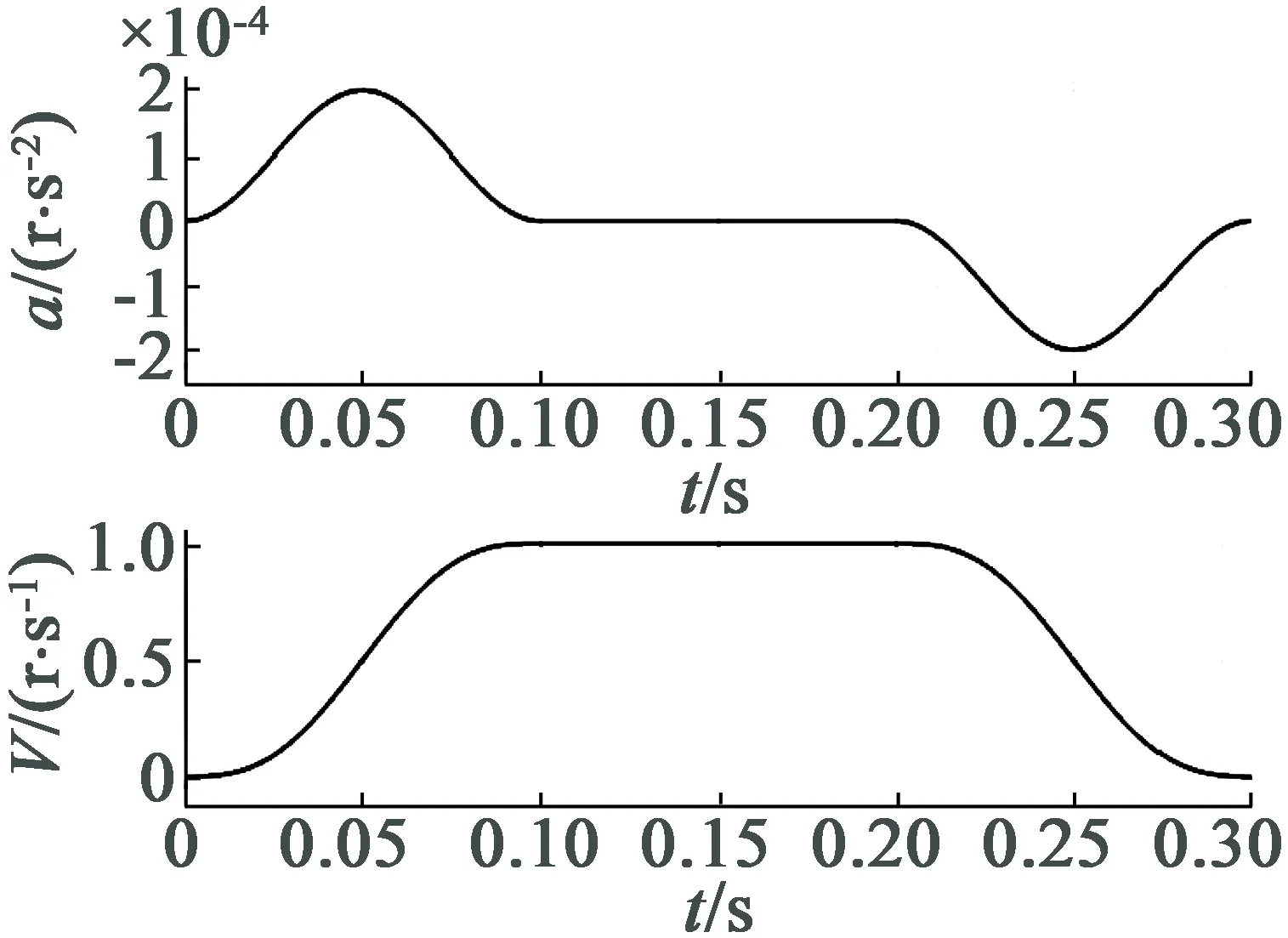
图5 正弦加速度S曲线仿真

3.2 矩频特性分析

合理的加减速曲线不但要满足速度与加速度的连续性，还要符合步进电动机矩频特性要求。加速过程中加速度所需要的转矩既不能超出电机矩频特性中的转矩要求，又要能够充分利用各个频率下步进电动机所能提供的转矩。

运行频率较低时，步进电动机输出转矩较大且稳定，当电机运行频率大于最大运行频率f1后，电机的输出转矩逐渐变小，如图6所示。

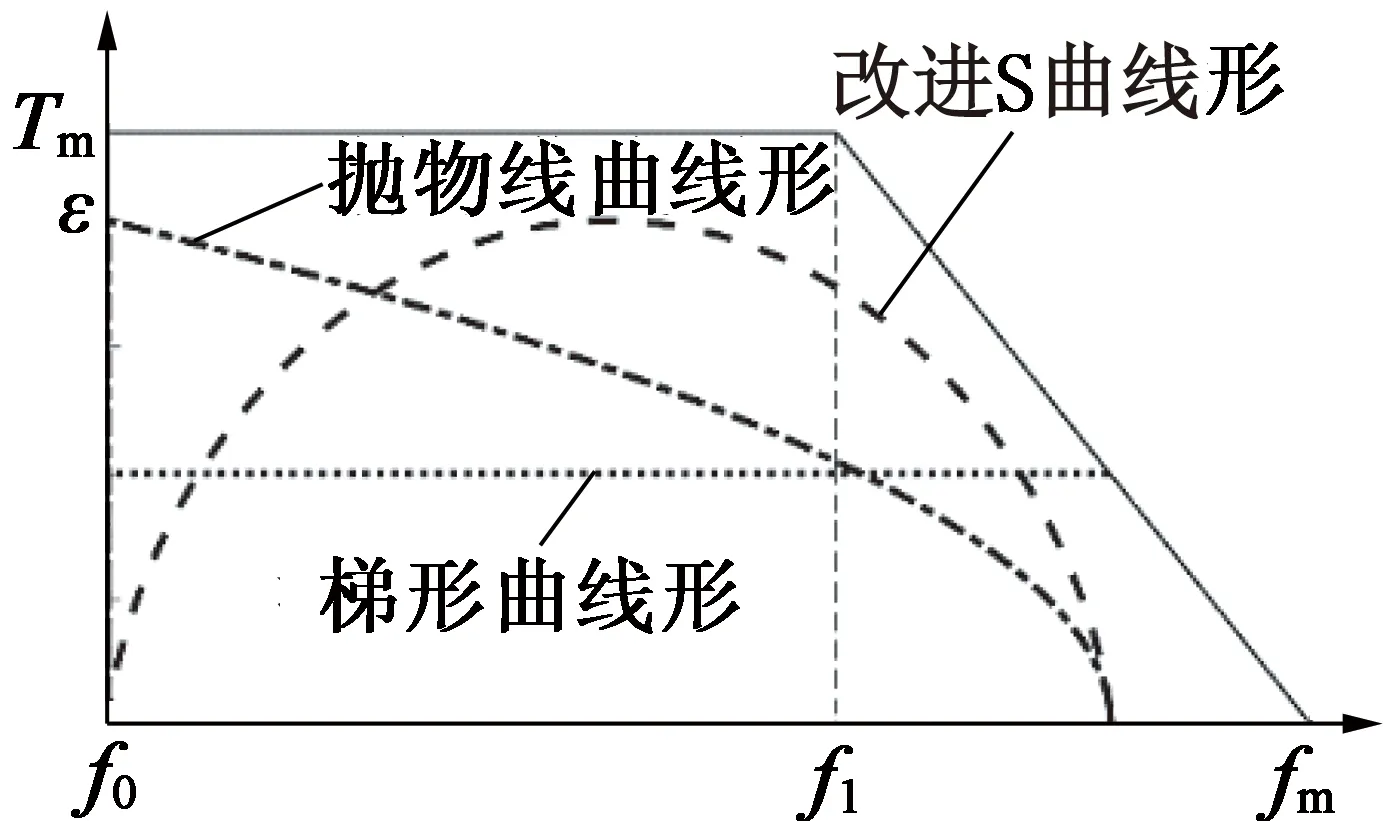
图6 加速度频率特性

将正弦加速度S曲线的加速度频率特性和梯形、抛物线以及电机矩频特性曲线进行对比分析发现，相比于梯形和抛物线速度曲线，正弦加速度S曲线的角加速度ε随驱动脉冲频率f快速增加时能够平滑过渡，这样在提高系统快速性的同时，减小了对系统的冲击。另外，在整个升速频段内能够更加充分利用电机提供的有效转矩。

4 步进电动机运行仿真

使用恒流斩波细分控制模型分别对梯形、抛物线和正弦加速度S曲线3种步进电动机加减速模式进行仿真，获得电机相电流与角速度波形，如图7所示。选择转子齿数50，步距角1.8°，保持转矩0.23 N·m，转子惯量35 g·cm2,额定相电流1.5 A，绕组电感3.2 mH的两相混合步进电动机。控制器采用256细分驱动，电机目标转速为5 r/s，加速时间和减速时间均设置为0.1 s，电机整体运行时间为0.3 s。电机两相电流相位差90°，幅值按正弦规律变化的同时，频率按照设计曲线要求连续变化，电机转速波形符合设计曲线要求，证明细分恒流斩波电流控制策略能实现对电机不同加减速方案的控制。

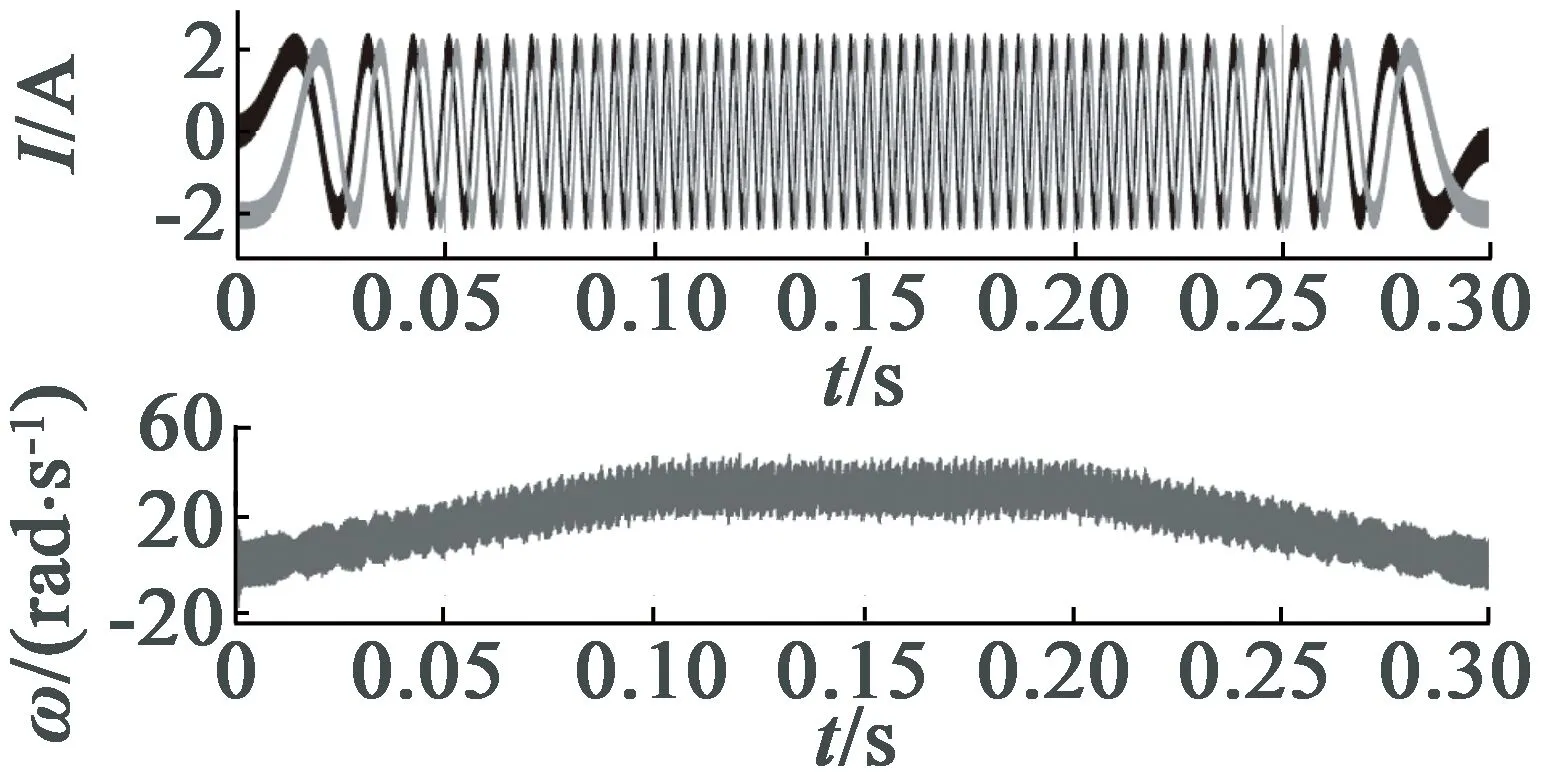
(a) 梯形

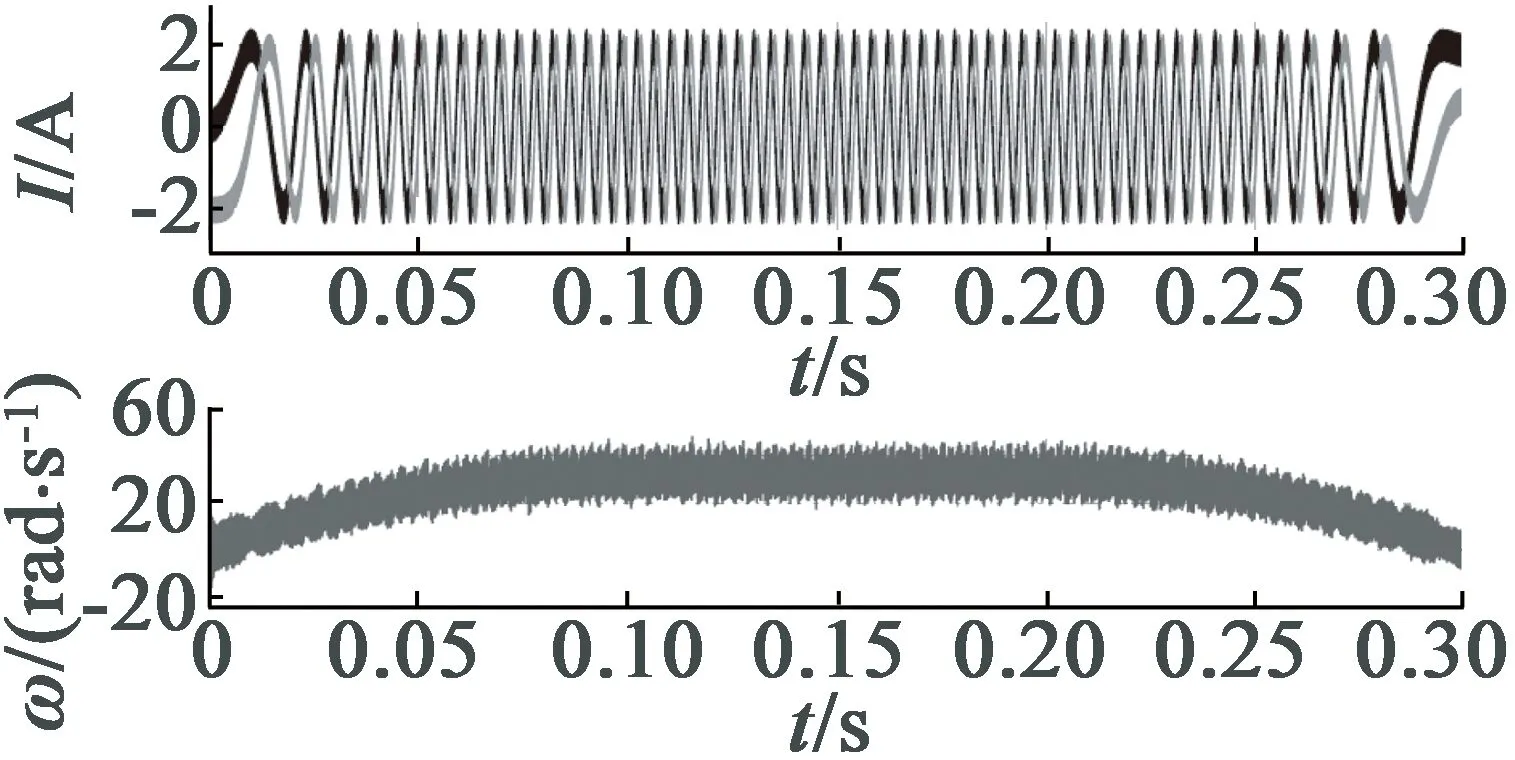
(b) 抛物线形

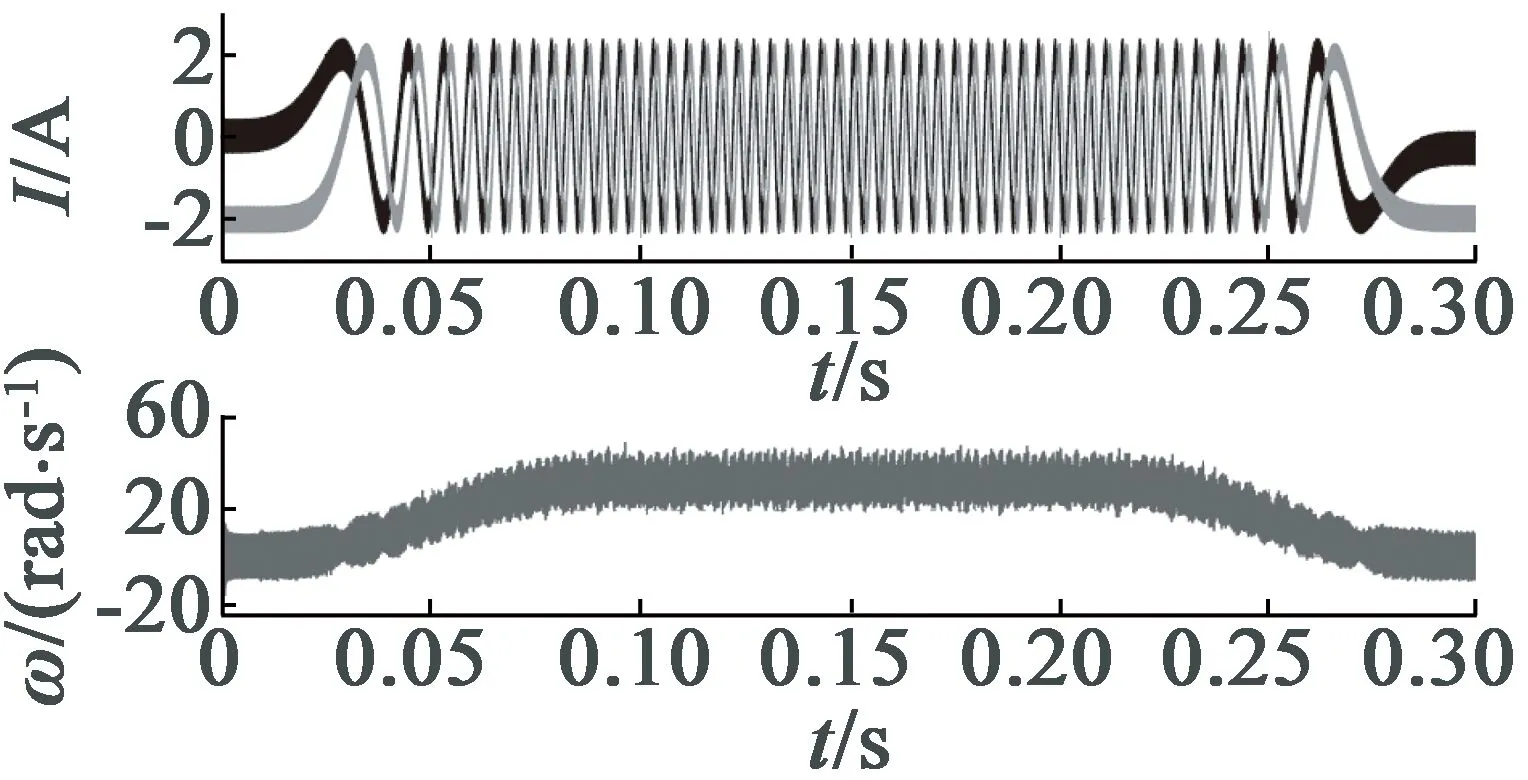
(c) 正弦加速度S曲线

在相同目标转速和相等加减速时长下，对比梯形、抛物线和改进S曲线升降速策略下的电机位置输出曲线，如图8所示，抛物线速度曲线具有提速与减速快的特点，相同运行长度下有着最大输出转角，正弦加速度S速度曲线和梯形速度曲线加减速效率相当。

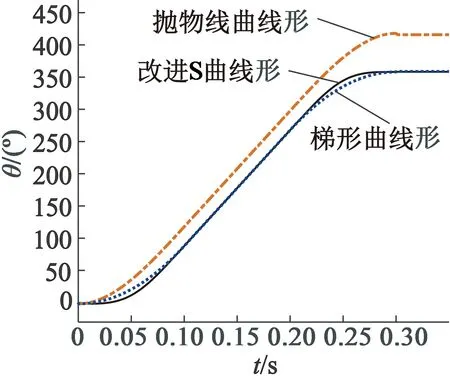
图8 电机运动位置仿真

进一步研究速度曲线对电机振荡的影响。分别在不同的电流细分数下，对梯形、抛物线、5段S曲线和正弦加速度S曲线进行电机停止阶段的残余振荡幅度分析，仿真结果如表1所示。由对比数据发现，抛物线法在不同的细分电流情况下电机运行终点处的位移振幅均较大，加速度突变对电机带来了较大冲击；而优化后的S曲线在终点处电机位移振荡幅度均小于其余几种升降速方案，电机运行更加平稳，柔性冲击小。

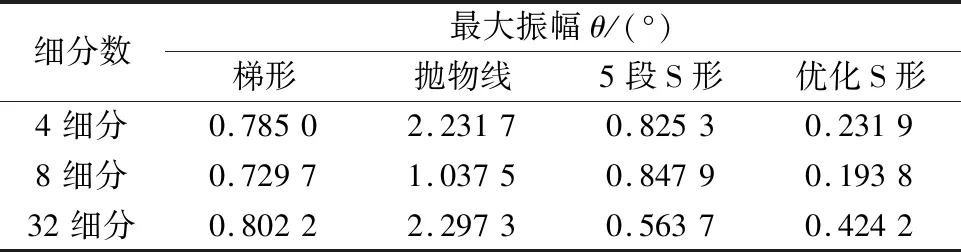
表1 不同速度曲线下最大残余振荡幅度比较

5 结 语

本文从两相混合式步进电动机的电气与机械特性分析出发，构建了基于相电流正弦细分策略的恒流斩波步进电动机开环控制模型，提高电机运行稳定性和控制精度。通过对步进电动机升降速方案进行对比分析表明，传统速度曲线法存在着速度曲线不光滑、加速度曲线突变不连续的现象，对电机带来柔性冲击。正弦加速度S曲线改进方案，其加速度为正弦函数形式，具有平滑连续可导特性，提高电机运行的平稳性。改进后的S速度曲线转矩特性更加优良，加速度会随着电机起动转速的变化而连续变化，并能够充分利用加速过程中电机提供的有效转矩。在相同运行条件下采用正弦加速度S曲线，电机起停更加平稳，电机振动小。仿真结果表明，基于正弦加速度S曲线升降速下的步进电动机细分控制策略能够改善电机运行稳定性，提高电机开环控制精度，适用于对电机运行平稳性和位置精度要求较高的场合。