深圳市抽水蓄能电厂的调速系统设计与应用

李青, 万波, 胡振恺, 沈燕

(深圳蓄能发电有限公司， 深圳 518172)

0 引言

调速控制系统是抽水蓄能电站的核心，承担机组启动、停止、工况转换和负荷调整的任务，关系到机组、电网运行的安全和稳定。传统PID型调速系统依赖于机制运行工况，难以适应工况大范围波动的需求，也不能对未来工况进行预测。基于上述情况，国内学者将分数阶PID控制、模糊控制、模型预测控制等方法应用于调速控制系统中，虽然可以满足工况大范围变化的运行需求，但不能准确描述水轮机的实际工况[1]。基于上述情况，本文利用机组动态特性的水轮机全特性曲线，从抽水蓄能机组工况频率调节和负荷开度调节方面，提出适合抽水蓄能电厂机组工况的非线性预测控制方法。该方法由3个子模型(描述管道弹性水击效应的二阶水击模型、基于饱和限幅的液压执行模型和基于发电机转子运动特性的一阶发电机模型)构成，可以减少水轮机全特性曲线反复迭代插值的数量，并对系统中水轮机未来工况预测的信息序列进行优化。

1 建立抽水蓄能机组调速系统的非线性模型

抽水蓄能机组调速系统由控制器、液压执行机构、引水系统、水轮机和发电机5部分组成。在对控制器进行优化时，要结合其他4部分来分析，所以要将整个装置作为研究对象，构建整体的非线性模型[2]，如图1所示。

1.1 液压执行机构

液压执行机构模型采用主接力器进行函数模拟传递，并控制速率限制、开度限制等非线性因素，形成内部闭环结构[3]，如图1所示。

1.2 引水管弹性水击模型

为了准确描述长引水管动态特性，需要构建弹性水击模型，掌握引水管道的水击效果，其计算如式(1)。

(1)

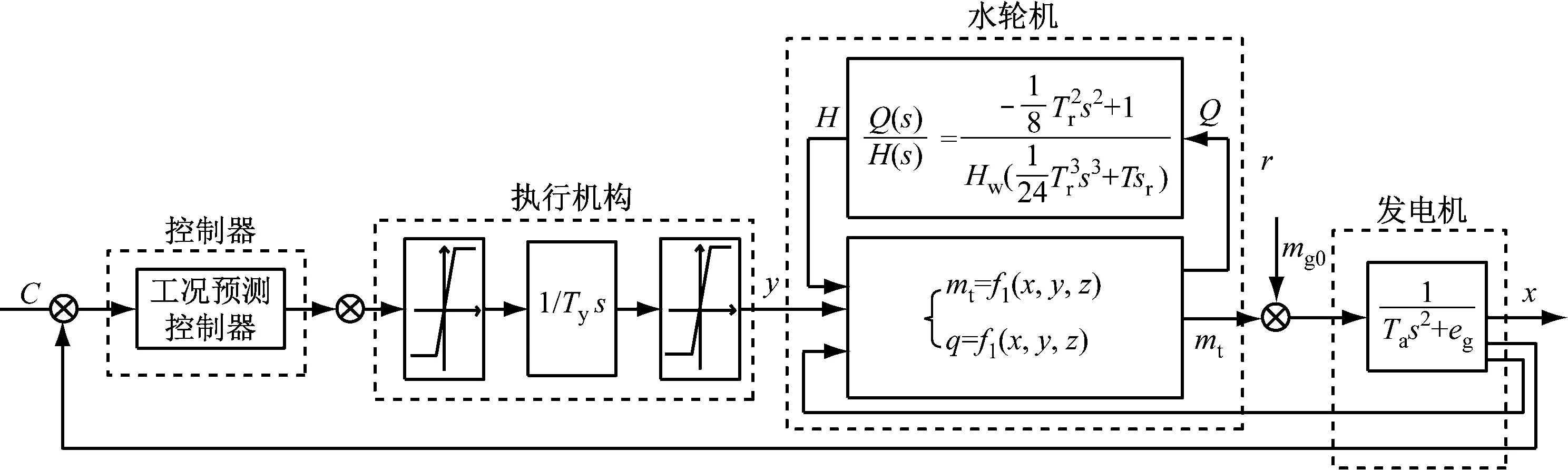
图1 非线性预测控制下的调速系统模型

其中，Tr为水击相长，Hw为引水管道特性系数。

1.3 水轮机非线性插值模型

为确保抽水蓄能电站安全运行，需要进行水轮机全特性曲线分析。水轮机飞逸工况和制动工况区呈现“S”型特征，而水泵工况区呈现交叉、重叠线性，如果直接应用曲线进行插值计算，会影响计算结果的准确性，或者由于其存在多值，而无法进行插值计算。因此，需要借助Suter法进行处理，将导叶开度作为参数，将全特性曲线转化为Suter曲线[4]，减少全特性曲线在水泵区和反水泵区的交叉和重叠现象。利用Suter法将实测的单位流量函数Q11=f1(α，n11)和单位力矩函数M11=f1(α，n11)转化为以x、y为参数的周期变化性函数WH(x,y)、WM(x,y)，计算如式(2)、式(3)。

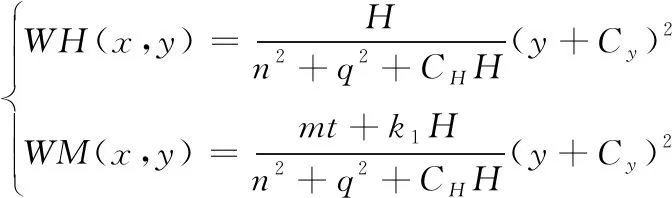
(2)

和

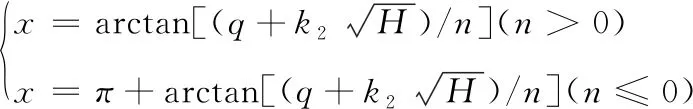
(3)

其中，H、n、q、mt分别为水头、转速、流量和转矩的相对值，经过Suter变化后，对应参数为k1、k2、Cy、CH。

1.4 发电机组模型

发电机采用反应转子运动特性与机组自我调节能力的一阶发电机算法，其空载运行时的微分描述如式(4)。

Tadw/dt+enw=mt-mg0

(4)

其中，en为机组自动调节系数，w为转子转速的偏差值，mt为机械功率偏差值，mg0负荷变动值，Ta电机的总惯性系数。

2 抽水蓄能机组非线性预测方法

传统PID调速控制系统采用频率调节和开度调节模式，进行机组空载工况调节和负荷工况调节。在负荷工况调节过程中，控制系统对水轮机的转速偏差和导叶开度偏差进行计算，并将水轮机稳定转差系数加在PID的积分值上，使水轮机的导叶开度值等于预设值[5]。这种基于PID法的控制方式存在两点不足，一点是在工况大幅变化的情况下，PID参数由于对工况数据值的过度依赖，不能进行事先预测，影响控制效果；二是PID控制系统依据当前和过去检测信号的偏差量计算即时控制率，缺乏对工况未来状态的预测。基于上述分析，本文提出基于模糊PID结构的非线性预测方法，对抽水蓄能机组的控制参数进行设定，使其适应于包括水轮机空载、运行、机组并网、负荷调节在内的多个典型工况。预测控制器在求解t时刻的即时控制率时，分为2步。

步骤1 ：求取模糊PID控制器在t时刻的实时参数。

由于出力调节过程监测的两个状态量转速和开度，构造模糊推理机输入e(t)和ec(t)，结果如式(5)。

(5)

其中，e(t)为t时刻水轮机输入，ec(t)为t与t-1时刻水轮机输入值，wref为水轮机最大转速，w(t)为t时刻水轮机转速；bp为转差系数；y(t)最大导叶开度，yref为t时刻导叶开度。

运用模糊计算法得到当前工况下，PID控制系统的三个预整定参数ΔKp,ΔKi,ΔKp， 如式(6)。

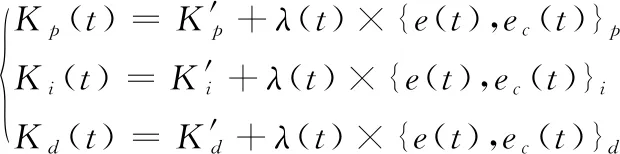
(6)

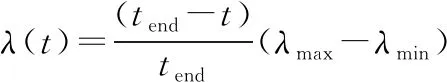
步骤2：将第一节中的调速控制模型作为预测模型，将步骤1中得到的模糊PID参数作为控制参数，对系统未来时间内状态进行预测性计算，并得到调速器控制增量序列 {Δu(t/t)，…，Δu(t+i-1/t)，…，Δu(t+Np-1/t)}。预测控制增量的计算步骤如下：

(1)计算PID在t时刻的第i个预测时域的控制率增量u(t+i-1/t)和控制率Δu(t+i-1/t)，如式(7)。

Δu(t+i/t)=Kp[Δw(t+i/t)-Δw(t+i-1/t)]+

KiΔT[Δw(t+i/t)-bpΔy(t+i-1/t)]+

Kd/ΔT[Δw(t+i)-2Δw(t+i-1)+Δw(t+i-2)]

(7)

其中，bp为永态转差系数，在空载和开机时为0，并网和负荷时为0.06。 将式(7)中获得的控制率带入图1中的执行机构模型中，可以得到预测时域i的导叶开度偏差相对值y(n+i)；

(2)引水系统、叶轮机和发电机间存在耦合关系，可以依据调速系统在第i-1预测时段获得w(n+i)，Q(n+i)，H(n+i)，mt(n+i)的状态量和y(n+i)。通过对流量Q、转速w的迭代计算，可以得到i+1个预测采样时刻的系统状态量w(n+i+1)，Q(n+i+1)，H(n+i+1)，mt(n+i+1)。

(3)对i是否等于预测时长Np，如果i=Np，那么t时刻的状态预测结束；如果i≠Np，则i=i+1，并循环执行(1)-(3)步骤。

(4)通过对已求得的预测控制增量序列{Δu(t/t)，…，Δu(t+i-1/t)，…，Δu(t+Np-1/t)}进行非线性衰减加权处理，得到当前时刻预测控制器的即时控制率u(k)的值，如式(8)。

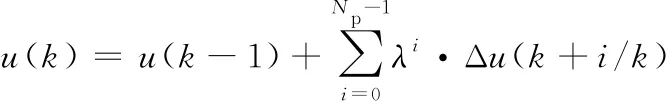
(8)

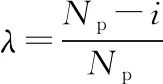
3 调速系统设计的仿真分析

以深圳抽水储能电站机组调速系统为研究对象，进行非线性模型仿真分析，电站基本额定参数如表1所示。

表1 深圳抽水储能电厂额定参数

3.1 水轮机开机过程仿真

依据深圳抽水蓄能机组的实际运行经验，设定开机过程的仿真控制策略。在开机过程初期阶段，当机组转速<90%的额定转速(频率=45 Hz)时，水轮机导叶以恒定速度进行一段式线性开启，达到空载限制开度后保持不变，待机组转速达到90%时，机组转入预测控制。其中，预测控制器的相关参数如表2所示。

表2 工况预测控制器的相关参数

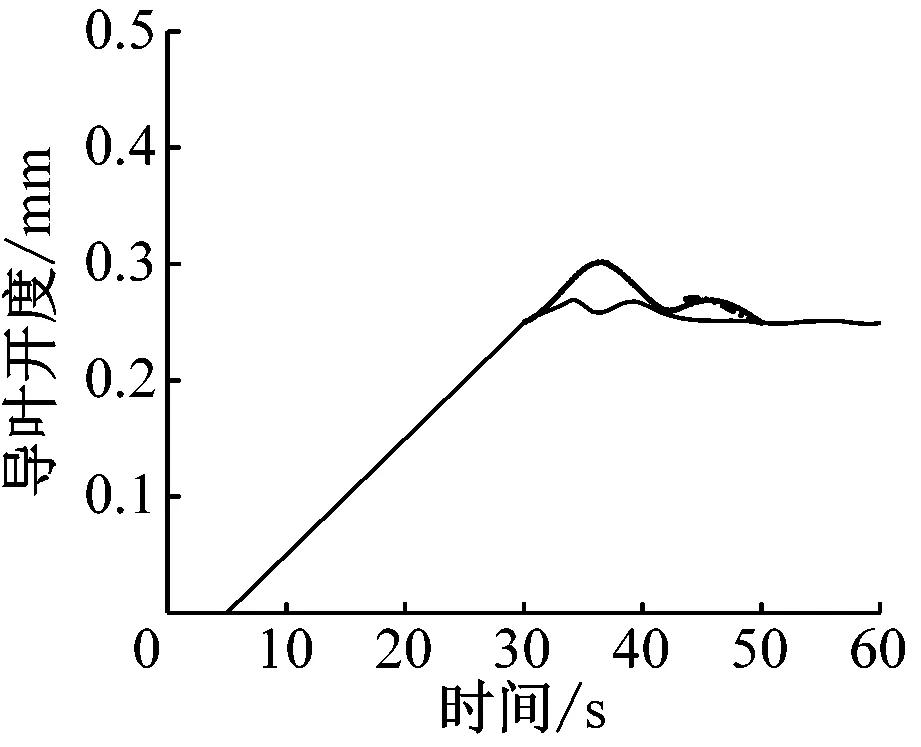
分别采用传统PID开度调节、模糊PID开度调节和非线性预测控制法，对深圳抽水储能电厂的水轮机工况进行仿真分析，仿真结果如图2所示。

A B

C D

从图2中的A、C图可知，单纯对PID控制器进行参数的模糊自适应调整，虽然可以在一定程度上调节机组开机的导叶开度和转速，但整体上仍然与PID控制效果一致。本文提出的非线性预测控制方法，利用每个采用周期中对水轮机未来系统状态的预测，得到预期时域内的转速累计偏差，并进行反馈控制，有效减少调节增量，缩短调节时间。由图2中的B、D可知，在机组转速达到90%额定转速后，控制策略能有效降低系统转入闭环控制时机械的转矩和水压波动幅度，缩短由开机暂态转为空载稳定运行的时间。上述分析可知，非线性预测控制方法可以有效地控制深圳抽水储能机组的发电方向开机。

3.2 减少25%负荷调节过程仿真

在由100%额定负荷向75%额定荷载转换的过程中，对单台抽水蓄能机组进行PID开度调节、模糊PID开度调节和非线性预测控制调节，并比较3种方法的仿真结果，如图3所示。

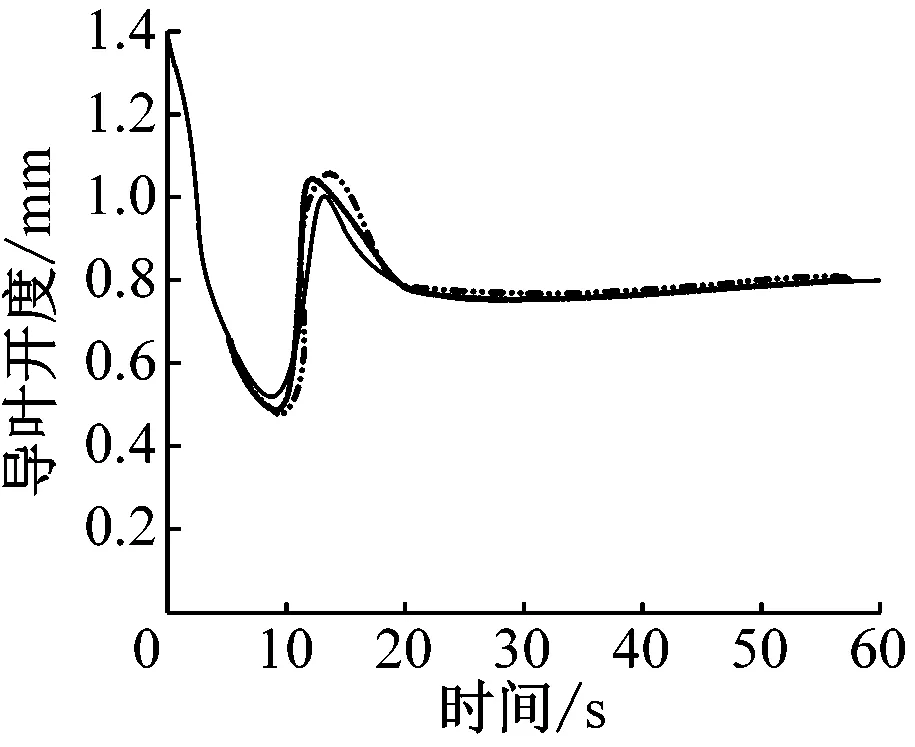
A B

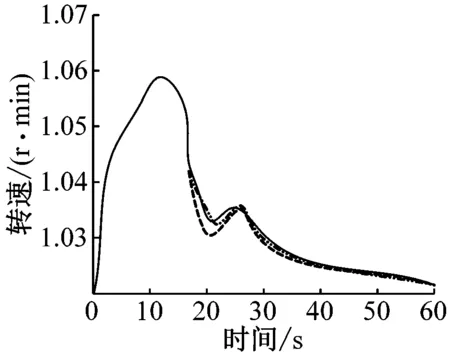
C D

由图3中A可知，非线性预测控制下的导叶开度由负荷额定开度降低至新的稳定状态时，震荡衰减更快，阻尼特性更强；由图3中B可知，在组织负荷发生变动方面，非线性预测控制下的抽水储能机组较PID控制机组，由负荷不平衡引起的上升状态中恢复更快，第二次转速波动后的转速恢复时间更短，调节增量更少；由图3中B、D可知，非线性控制下的机组的水轮机转矩更小，引管内的水压波动更低。

综上仿真结果，本文提出的非线性预测控制方法在深圳抽水蓄能电厂的机组负荷变化方面，优于传统PID控制法，并在一定程度上抑制转速上升量和水压波动量，调节效果比较理想。

4 总结

本文针对深圳抽水储能电厂情况，提出适用于机组调速系统的非线性预测控制方法，对机组不同工况下有限时域内的系统控制增量和状态量进行预测，优化PID控制中的滚动计算过程，减少在线计算量；应用非线性递减加权方法，对时域内的预测控制增量进行累加计算，使调速控制器的即时控制率中包含对调速系统未来工况的预测信息，弥补传统PID控制器在对机组未来工况缺乏预测的不足。分别利用非线性预测方法、PID控制法、模糊PID控制法，对深圳抽水蓄能机组发电方向开机过程、负荷调节过程进行仿真分析，结果验证了非线性预测控制法在抽水蓄能机组发电方向、不同负荷调节方面的有效性和优越性。