基于特征匹配和MCL的全局融合定位算法研究

章洋 李星博 胡丁文 杨帆 兰长勇

摘要：传统的蒙特卡洛定位（Monte Carlo Localization， MCL）算法在实时性以及定位精度上，都还存在改进的余地。通过将特征匹配和蒙特卡洛定位进行融合，对基于特征匹配和MCL的全局融合定位算法进行了研究。融合定位算法在蒙特卡洛定位的基础上，增加了线段特征匹配的过程，用于缩小定位的范围，从而改善定位精度和实时性。在MATLAB软件以及机器人的测试实验中，通过三角形运动路径来对比蒙特卡洛定位算法与融合定位算法的定位精度，实验结果表明融合定位算法的定位精度比蒙特卡洛定位算法提高了78%。

关键词：蒙特卡洛定位;激光雷达;全局定位;特征匹配;机器人操作系统

中图分类号：TP242.6    文献标识码：A

文章编号：1009-3044（2019）19-0186-03

Abstract： The traditional Monte Carlo Localization algorithm still has room for improvement in real-time and positioning accuracy. By combining feature matching and Monte Carlo positioning， the global fusion localization algorithm based on feature matching and Monte Carlo is studied. Based on Monte Carlo Localization， the Fusion Localization algorithm increases the process of line segment feature matching， which is used to narrow the localization range， thus improving localization accuracy and real-time performance. In the MATLAB software and robot test experiments， the localization accuracy of Monte Carlo Localization algorithm and the Fusion Localization algorithm is compared by the triangle motion path. Experimental results show that the localization accuracy of the Fusion Localization algorithm is 78% higher than that of Monte Carlo Localization algorithm.

Key words： Monte Carlo Localization; Lidar; Global Localization; Feature Matching; Robot Operating System

移動机器人定位是指机器人通过感知获取环境信息，经过相关的信息处理而确定自身及目标位姿的过程[1]。机器人导航的相关问题更形象的一种表达方式是：“我在哪儿”“我要去哪儿”及“我如何到达那儿”[2]，而其中的第一个问题“我在哪儿”即机器人的定位问题，是实现机器人导航的前提。针对这一实际问题，前人已经提出了许多机器人定位的方法，例如比较流行的基于概率的定位方法和基于地图的定位方法[3]，尤其是基于概率的机器人定位方法，近年来受到大量学者的关注[4]。现有的研究和应用表明：概率定位方法是一种能够有效实现巡检机器人精确定位和自主导航的方法[5]。而基于概率的定位方法中，蒙特卡洛定位算法由于其较高的计算效率，在许多场景中得到应用。在文献[6]中，Dellaert等人基于马尔可夫定位方法，提出了一种利用粒子群描述概率分布的方法，即粒子滤波（particle filter， PF）算法。PF算法保留了马尔可夫定位法定位精度高的特点，同时，该算法易于实现，对硬件运算资源的要求较低，由于PF算法是受蒙特卡洛思想的启发，Dellaert等人也将这种定位方法称为蒙特卡洛定位，并且这一术语已经成为移动机器人定位研究领域的通用说法。但是经典的蒙特卡洛定位算法存在定位失效和机器人绑架的问题，很多学者针对这一问题提出了改进的方法，其中Fox等[7]人提出了自适应蒙特卡洛定位（Adaptive Monte Carlo Localization， AMCL）算法，AMCL有效地解决了MCL算法存在的定位失效的问题。

基于以上分析，本文对基于特征匹配和MCL的全局融合定位算法进行了研究。全局融合定位算法以开源机器人操作系统（Robot Operating System，ROS）的机器人为平台，首先使用线段提取（Line Segment Detector， LSD）算法[11]提取全局地图的特征数据，然后使用分开合并（Split-and-Merge，S-M）算法[12]提取机器人采集的激光雷达传感器数据中的线段特征，再将这些特征数据与数据库中存储的全局地图的特征数据进行匹配，匹配后可以得出机器人当前位姿的一个估计值，将这一位姿估计值应用于MCL算法中，这样大大提高了MCL算法的收敛速度，最终实现机器人的快速全局定位。

1 移动机器人全局定位算法

本文在MCL的基础上引入特征匹配实现融合定位功能，融合定位的主要思想是将特征匹配估算的位姿作为MCL算法中粒子群的初始位姿，融合定位算法流程如下所示：

步骤1：生成栅格地图的特征数据库。将栅格地图转换为二值图像，使用LSD算法提取栅格地图的所有线特征，组成栅格地图的特征数据库;

步骤2：生成实时特征。将激光雷达的扫描数据进行分区，使得分区后每个区域内都包含一条连续的线段特征，对每个区域内的数据使用分割-合并算法提取出区域内的线段特征;

步骤3：生成预测位姿集。根据实时特征中其中一条线段的线段长度，查找特征数据库中相同线段长度的线段特征，得到若干个预测位姿，将这些位姿组成预测位姿集;

步骤4：生成最优预测位姿。将激光雷达生成的原始扫描数据按预测位姿集中的位姿进行转换，使得所有扫描数据转换到全局地图坐标系下，计算扫描数据与全局地图的距离[Dj]：

[Dj=i=1Pdi]

其中，[Dj]为预测位姿集中第[j]个位姿对应的距离，[di]为扫描数据中第[i]个数据点距最近栅格点的距离，[P]为扫描数据中数据点的总数。最终，计算预测位姿集中所有位姿对应距离的最小值[Dmin]，最小值[Dmin]所对应的位姿作为最优预测位姿。

[Dmin=minD1，…，DN]

其中，[N]为预测位姿集的个数。

步骤5：根据最优预测位姿初始化MCL算法的粒子群，生成[M]个粒子。其中粒子的位姿初始化为最优预测位姿，所有粒子权值初始化为[1M]，应用测量模型计算粒子权重，计算粒子群的平均权重;

步骤6：判断粒子群的平均权重是否大于阈值，如果大于阈值，则进入步骤7，否则，返回，步骤2;

步骤7：应用运动模型估计粒子位姿。机器人产生位移，同时激光雷达产生一帧新的数据，使用运动模型的采样函数[pxtxmt-1，ut]对粒子的位姿信息进行更新，

[xt[m]?pxtxmt-1，ut]

其中，[xmt-1]表示[t]-1时刻粒子群[χt-1]中第[m]个粒子的位姿，[ut]表示从[t]-1时刻至[t]时刻之间机器人的运动数据，[xt[m]]表示[t]时刻该粒子的位姿;

步骤8：用测量模型计算粒子权重。使用测量模型的采样函数[pztxmt，m]计算粒子的权重值

[wmt?pztxmt，m]

其中，[zt]表示激光雷达[t]时刻的测量数据，[wmt]表示该粒子的权重值;

步骤9：估计位姿。计算粒子群[χ′t]中粒子的位姿期望得到估计位姿[xt]

[xt=m=1Mwmtxmt]

步骤10：粒子群重采样。

综上所述，基于特征匹配和MCL的全局融合定位算法的流程图如下图1所示：

2 实验及仿真结果

在测试全局定位时，将真实环境的栅格地图导入进来，在ROS系统上机器人按照固定的运行指令进行运动，机器人身上的传感器记录数据同时人为的记录真实路径，在MATLAB上分别通过蒙特卡洛定位和本文提出的融合定位两种定位方法计算出估计路径，对于定位误差的评估分别使用位置误差[εi]和路径误差[εp]来描述。位置误差的定义为

[εi=xi-xi2+yi-yi2]

其中，[εi]表示路径上第[i]次采集数据的位置误差，[xi]表示第[i]次采集数据时[x]方向的真实坐标，[xi]表示第[i]次采集数据时[x]方向的估计坐标，[yi]表示第[i]次采集数据时[y]方向的真实坐标，[yi]表示第[i]次采集数据时[y]方向的估计坐标。

路径误差[εp]定义为路径中位置误差的均方根误差

[εp=i=1Nε2iN]

其中，[εi]为路径上第[i]次采集数据的位置误差，[N]为路径上采集数据的总次数。

本次实验的真实环境是电子科技大学清水河校区科研楼B区2楼217附近的空间区域，机器人运动路径在真实环境中示意图，如图2所示。

3 结论

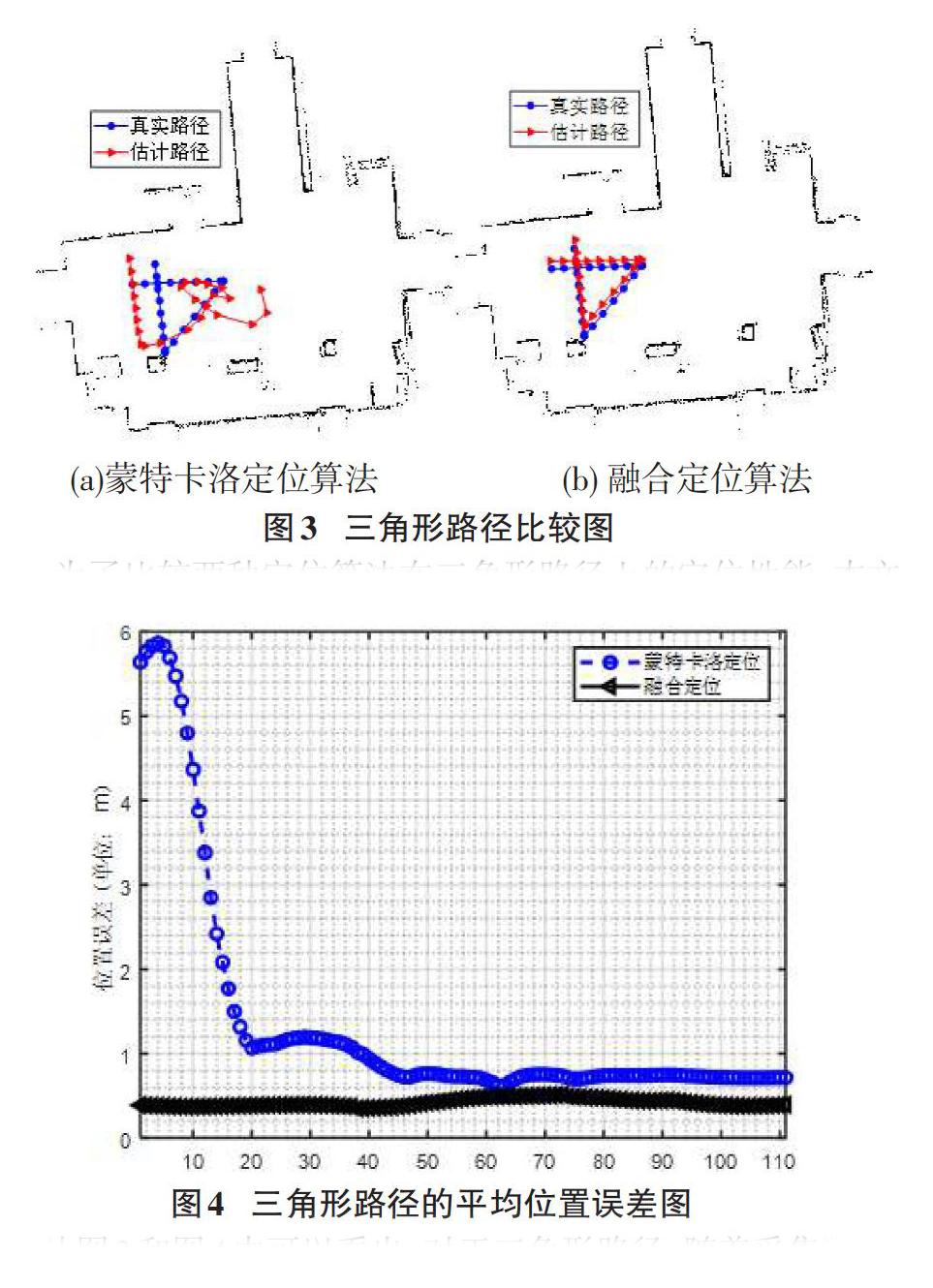
本文在传统的蒙特卡洛定位上，针对全局定位存在收敛时间，且路径误差较大，通过引入线段特征匹配，完成位姿的最初估计，再使用蒙特卡洛定位完成位姿跟踪，对基于特征匹配和MCL的全局融合定位算法进行了研究，在真实环境中，通过三角形的测试定位路径，并对测试路径分别测试20次，完成全局定位的测试。通过测试数据，我们发现融合定位的平均位置误差都小于蒙特卡洛定位的平均位置误差，不存在定位收敛時间，在路径误差上，融合定位的平均路径误差比蒙特卡洛定位提高了78%。

参考文献：

[1] 王鹏，李书杰，陈宗海. 移动机器人定位方法研究综述[C]. 第13届中国系统仿真技术及其应用学术年会，安徽，中国， 2011， 911-915.

[2] Leonard J， Durrant-Whyte H F. Mobile robot localization by tracking geometric beacons[J]. IEEE Transactions on Robotics and Automation， 1991， 7（3）： 376-382

[3] 张弦，苏志远. 自主移动机器人定位技术研究综述[J]. 机电产品开发与创新， 2010， 23（2）： 3-5.

[4] 时也，吴怀宇，徐文霞，等. 基于扩展卡尔曼滤波器的移动机器人SLAM研究[J]. 电子设计工程， 2012， 20（1）： 104-106.

[5] 操凤萍，啟要. 基于自适应蒙特卡洛算法的实时定位研究[J]. 计算机工程， 2018， 4（9）： 8-32.

[6] Dellaert F， Burgard W， Fox D. Monte Carlo Localization for Mobile Robots[A]. IEEE International Conference on Robotics and Automation[C]， 1999.

[7] Fox D， Burgard W， Dellaert F， et al. Monte Carlo Localization：Efficient Position Estimation for Mobile Robots[A]. National Conference on ArtificialIntelligence[C]， 1999： 343-349.

[8] Gordon N J，Salmond D J ， Smith A F M.Novel approach to nonlinear /non-Gaussian Bayesian state estimation[J].Proceedings F-Radar and Signal Processing，1993，140（ 2）： 107-113.

[9] 劉松国，朱世强，刘瑜，等. 移动机器人的蒙特卡罗自主定位算法研究[J]. 机电工程， 2005， 22（4）：38-42.

[10] Doucet A， Godsill S. On Sequential Monte Carlo Sampling Methods for Bayesian Filtering[R]. Cambrige： University of Cambrige， 1998： 1-36.

[11] R G Von Gioi， J Jakubowicz， J M Morel， et al. LSD： a line segment detector[J]. Image Processing On Line， 2012， 2： 35-55.

[12] V. Nguyen， A. Martinelli， N. Tomatis， et al. A comparison of line extraction algorithms using 2D laser rangefinder for indoor mobile robotics[C]. 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton， Alta， 2005， 1929-1934.

【通联编辑：梁书】