基于系统层次模糊优化模型的工业用水定额合理性研究
2019-09-24刘曾美陈斯达冯斯安蓝福鹏
刘曾美,陈斯达,冯斯安,蓝福鹏
(华南理工大学土木与交通学院,广东 广州 510640)
随着经济社会的发展、产业发展情况结构的调整以及节水工作的不断深入,现行用水定额逐渐与水资源条件、社会经济水平、技术发展情况以及节水型社会建设产生了不协调[1-3]。对用水定额的合理性进行评估,及时掌握定额制定、修订、执行的情况,是不断规范并强化用水定额管理的重要手段[4]。
目前,用水定额合理性评估的方法可大致归纳为4种:①通过典型调查,采用对比(类比)法以及定额分析法评估定额的合理性,如,黄燕等[5]采用类比法和二次平均法对海南省城镇生活用水定额进行合理性评估;张丽等[6]参照《海南省工业及城市生活用水定额(试行)》及国内其他地区工业用水定额标准,采用主观概率值法和横向比较法对三亚市主要工业用水定额进行评估,分析三亚市现状工业用水节水潜力;韩云[7]通过与国家定额标准以及松辽流域内辽宁省、黑龙江省用水定额进行对比,分析吉林省定额的完整性和先进性,研究定额的代表性和规范性。这类方法简单直观,便于摸底了解,适用于定性分析。②采用层次分析法评判用水定额的合理性,如施胜利[8]运用层次分析法,以覆盖性、合理性、先进性、实用性、公平性为准则评判上海市用水定额的合理性。当指标太多时,这种方法的数据统计量大,权重也难以确定,并且出现一致性随机偏离的可能性也越大,此外,这种方法也没考虑合理性评判的模糊性。③将一些评价方法与层次分析法结合起来评判用水定额的合理性,如,刘紫薇[9]采用多层次灰色关联综合评判法从覆盖性、合理性、先进性、实用性4个方面对陕西省、宁夏回族自治区、内蒙古自治区、新疆维吾尔自治区以及青海省的农业用水定额进行评估;焦军[10]采用多层次灰色关联综合评判法计算黄河流域各省区现行的火电行业用水定额指标序列与最优指标集的相似程度,从而确定用水定额的相对优劣程度;赵博等[11]基于层次分析法和模糊综合评判法评价辽宁省用水定额的合理性;李奎等[12]通过云模型改进的模糊层次分析法构建黄河流域火电行业用水定额评估模型。这类方法考虑了合理性评判的模糊性,从整体角度更好地解决评估过程中的主观不确定性,但未进行模糊优化。④基于投影寻踪法对用水定额的合理性进行评估,如邓敏慧等[13]基于投影寻踪法对长江流域火电行业取用水定额进行了多目标评价。投影寻踪计算量大,尤其当用水定额涉及的指标较多时,计算复杂,而且有些问题尚有待合理解决[14-15],因此较少应用于用水定额评估。
无论是工业用水定额、居民生活用水定额还是农业灌溉用水定额,从系统工程的观点,均可视为一个由不同层次组成的独立系统,故用水定额评价便成为一个具有多层次结构的评价问题,并且用水定额评估具有模糊性,因此可将系统层次与模糊优化理论有机结合起来的系统模糊优化理论[16-17]引入解决用水定额的合理性评价问题,其隶属度通过优化得到,且隶属度函数概率化,具有数学理论严谨、物理概念清晰、评价结果避免均化等特点,更能客观地反映实际情况[16-17]。鉴于此,本文以江西省工业用水定额为例,基于系统层次模糊优化模型[17]对其合理性进行评估。
1 系统层次模糊优化模型
工业用水定额合理性评估要考虑实际用水水平、产业结构、节水工艺和水平衡测试等众多评估因子。设评估因子的集合为M,则可根据评估因子的不同属性将M分解为m个独立的子系统[17],且每个子系统分别有a1、a2、…、am个独立的评估因子。设第i子系统中第j个评估因子的评分值为xij,则第i子系统中ai个评估因子的合理性评分情况可用向量xi表示:
xi=(xi1,xi2,…,xiai)T
(1)
根据用水定额合理性的优劣程度,设这一层次划分有t个评估等级。评估等级标准以向量v来表示:
v=(v1,v2,…,vt)T
(2)
每个子系统分别以一定的隶属度u隶属于某一评估等级,第i子系统的隶属度可用模糊向量ui表示:
ui=(ui1,ui2,…,uit)
其中
(3)
由于每个工业用水定额合理性影响因子对评估结果的影响程度不同,因此需要根据其影响的相对重要性赋予不同的权重,以客观反映各评估的相对重要性。评估因子的权重向量wi表示:
wi=(wi1,wi2,…,wiai)
其中
(4)
于是第i子系统的评估因子的评分值向量xi与第l等级的差异可用考虑了影响权重后的广义距离来表达:
(5)
为了更好地表达第i子系统评估因子的分值与评估标准各等级之间的差异,在模糊理论中,可将隶属度定义为权重。为得到最优分级向量,取目标函数为第i子系统的评估因子分值向量与各等级标准之间的加权距离和最小,即以第i子系统与各等级标准之间的加权距离和最小为目标函数来优选第i子系统评估因子隶属于各等级的隶属度,即:
(6)
约束条件
线性优化求解得到第i子系统隶属于第l等级的隶属度:
(7)
最大隶属度max(uil)所对应的等级便为第i子系统的评估等级。这里隶属度uil可以理解为概率数,即相当于第i子系统的合理性评分值xi属于第l等级的概率。于是可求得i子系统的合理性评分期望值xiai:
(8)
式中t为评判等级数。由式(8)便可以求得这一层次的m个子系统的合理性评分值。
这m个子系统便成为高一层次的评判对象,这一层次的模糊优化等级评价方法完全与上相同,故可用式(7)求得这一层次各子系统隶属于各等级的隶属度。如果这一层为最高层次,取其隶属度向量中最大的那个隶属度所对应的等级便为用水定额合理性评估的等级。若这一层不为最高层,其隶属度向量便是更高一层次的模糊优化等级评价的依据,逐层类推,算到最高层次时隶属度向量中最大的隶属度所对应的等级即为用水定额合理性评估的等级。
2 实例分析
2.1 研究区概况
DB36/T 420—2011《江西省工业企业主要产品用水定额标准》包括34个工业大类,制订了281个工业产品用水定额标准,涵盖的工业类别用水量占工业总用水量的90%以上,覆盖范围较好。江西省主要工业用水行业包括高用水及高污染产业和地方特色产业两类。其中,高用水及高污染产业包括造纸、石化、纺织、金属冶炼及压延、火电、食品加工6类,用水量占工业总用水量的86.7%;特色工业行业包括陶瓷和稀土2类,用水量占工业总用水量的0.6%。
江西省工业用水占用水总量的23.51%。随着技术水平的提升和产业结构的调整,工业用水量增加趋缓。江西省规模以上工业企业用水主要集中在重工业,特别是集中于钢铁、建材、化工、纺织、火电、造纸六大高耗水行业。各工业行业用水比例见图1,1999—2013年地表水和地下水供用水量变化见图2,1999—2013年水资源总量变化见图3。
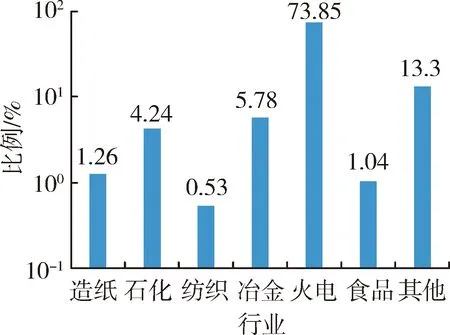
图1 各工业行业用水比例
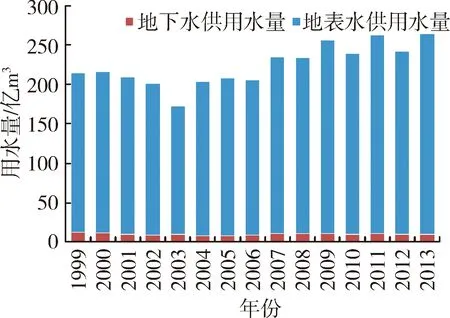
图2 1999—2013年供用水量变化
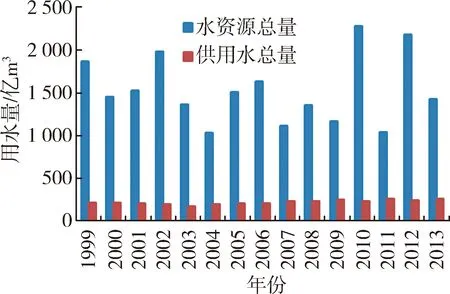
图3 1999—2013年水资源总量变化
2.2 层次结构
以江西省工业行业实际用水情况的调研资料为基础,结合《用水定额评估技术要求》和《项目节水评估技术导则》等相关标准的评估内容和标准,参考2016年最严格水资源管理制度考核内容、《重点工业行业用水效率指南》《江西省2015年水资源公报》等相关材料,分析其用水现状和水平,研究其影响和制约因素。以江西省工业用水定额合理性评估(T层)为最高层次的评判对象,把行业划分和定额制(修)订情况、产业结构特点、工业企业规模和工艺情况以及与现状用水水平对比情况4个子系统作为第二层(C层)评判对象,把第二层包含的各种因素(经筛选识别出)作为最低层(P层)的评判对象,构建江西省现行工业用水定额合理性评估系统的层次结构,见表1。
表1 工业用水定额合理性评判的层次结构

2.3 合理性评估
根据评估的特性将用水定额的合理性划分为7个评估等级:极差、差、较差、一般、较好、好、极好,相应取值分别为0、0.1、0.3、0.5、0.7、0.9、1.0。结合江西省用水现状和2016年最严格水资源管理制度考核自查报告,根据17位参与2016年最严格水资源管理制度考核的专家和工作人员给出的20个评判因子的评分值和权重以及4个评价指标的权重,计算得到各位专家评判的平均值见表2。
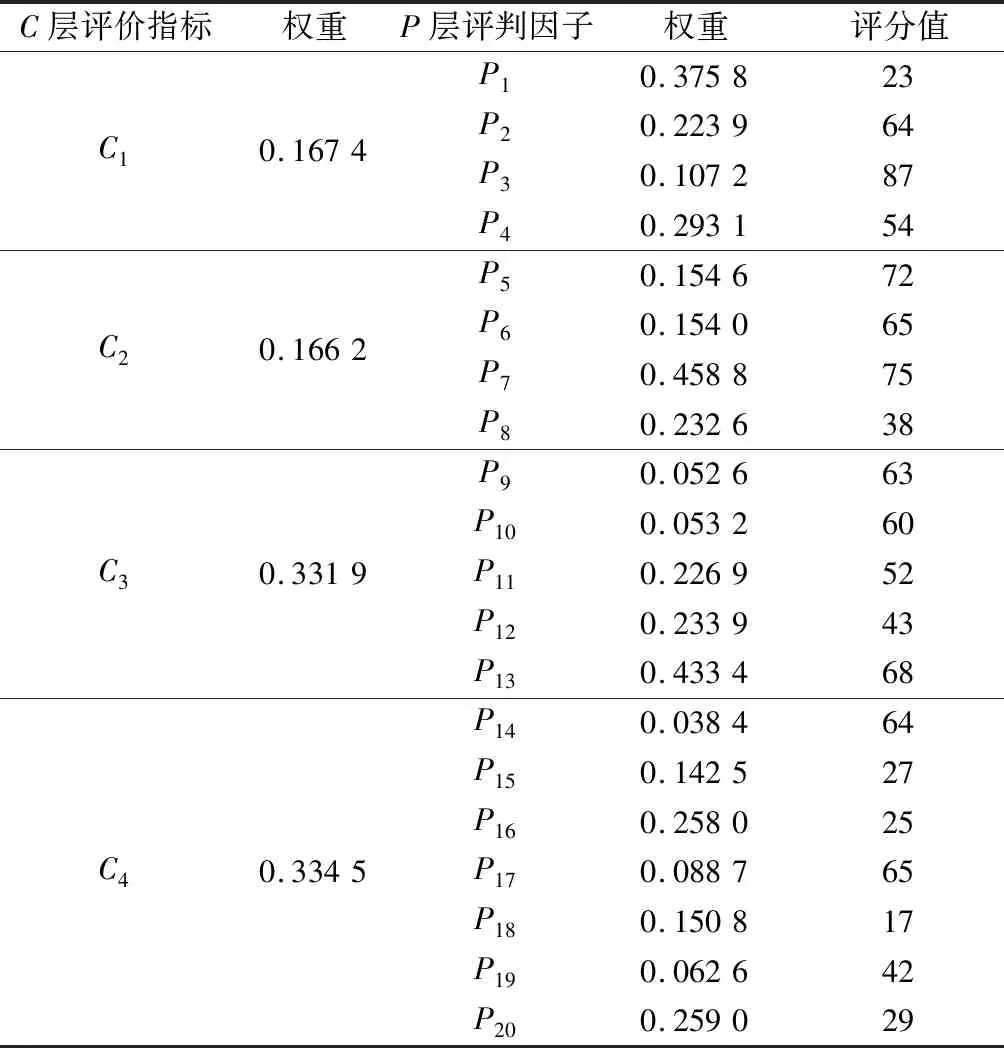
表2 专家评分值及权重
根据评判因子层的评分值向量、权重向量和等级向量,求得C层各子系统(即各评价指标)的隶属度向量分别为:u1=(0.091 8,0.115 8,0.188 9,0.239 8,0.173 1,0.105 5,0.085 1)、u2=(0.057 0,0.067 4,0.106 7,0.183 6,0.339 1,0.143 2,0.103 0)、u3=(0.057 3,0.069 2,0.118 9,0.298 5,0.274 0,0.103 3,0.078 8)、u4=(0.110 1,0.162 0,0.377 9,0.152 7,0.088 7,0.058 5,0.050 0)。计算得到C层次4个评估指标的等级期望值分别为0.489 4、0.599 8、0.555 4、0.370 7。
由此可见,行业划分和定额制(修)订情况C1的最大隶属度为0.239 8,所属等级为一般,其期望值为0.489 4,介于一般和较差之间;产业结构特点C2的最大隶属度为0.339 1,所属等级为较好,其期望值为0.599 8,介于一般和较好之间;工业企业规模和工艺情况C3的最大隶属度为0.298 5,所属等级为一般,其期望值为0.555 4,介于一般和较好之间;现状用水水平对比情况C4的最大隶属度为0.377 9,所属等级为较差,其期望值为0.370 7,接近较差等级值。
将C层各评估指标的等级期望值作为其评分值,根据评估指标层的评分值向量、权重向量和等级向量,求得江西省工业用水定额合理性评估总体的隶属度向量为u=(0.064 7,0.081 3,0.167 0,0.396 4,0.151 0,0.077 3,0.062 2),进而求得江西省工业用水定额合理性的总期望值为0.494 0。
由此可见,江西省工业用水定额总体评价的最大隶属度为0.396 4,所属等级为一般,数学期望值小于0.5,表明江西省现行工业用水定额的合理性属于一般,稍偏向较差。由于隶属度向量在该模型研究中的数学意义是各等级的概率分布,则江西省现行工业用水定额的合理性属于一般的概率为39.64%,属于较好的概率为15.10%,属于较差的概率为16.70%,属于好的概率为7.73%,属于差的概率为8.13%。
江西省现行工业用水定额的合理性一般,稍偏向较差,主要表现在与现状用水水平对比,江西省现行工业用水定额值与典型企业实际定额值对比明显偏高,其评分值仅为17。表3为江西省部分工业用水定额与典型企业实际用水定额值对比情况,可见与企业实际用水水平对比,这些定额标准明显偏高,其中,江西省定额标准远大于啤酒制造、普通钢、电解铝、包装纸和原油加工等产品的实际用水定额,浮动均超过了40%,合理性较差,难以在水资源管理中发挥作用,与本文研究结果相一致。
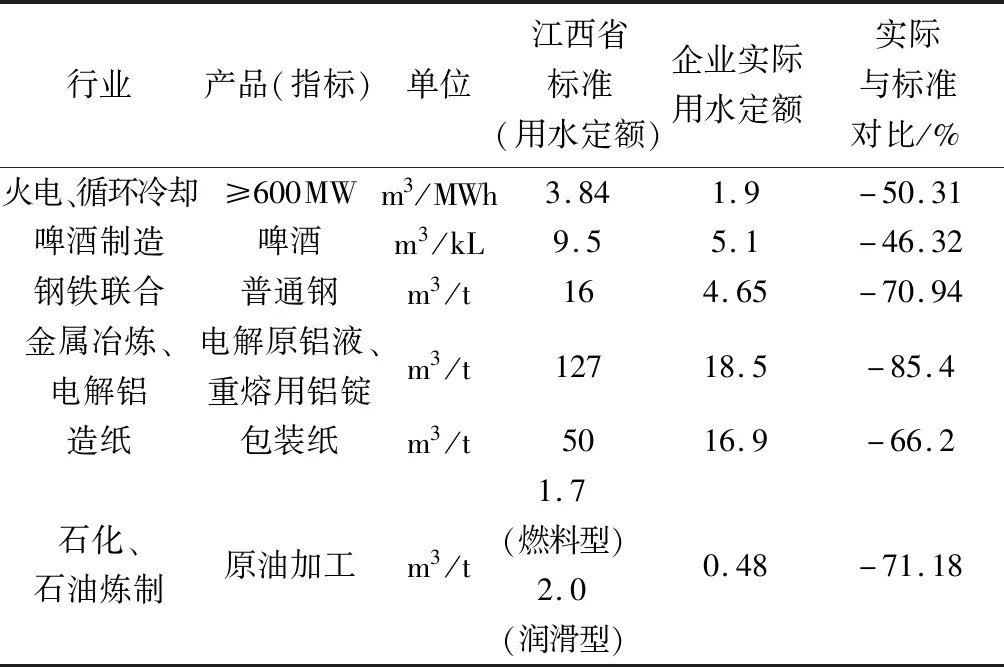
表3 江西定额标准与典型企业实际定额值对比
3 结 语
本文基于系统层次模糊优化模型评估江西省工业用水定额的合理性,结果表明将系统层次模糊优化模型用于用水定额的合理性评估是一条可行的途径。
