防冻胀护道型式对季冻区高铁路基冻结特征影响分析

2019-09-24

石家庄铁道大学学报(自然科学版) 2019年3期

(石家庄铁道大学河北省大型结构健康诊断与控制重点实验室，河北石家庄 050043)

0 引言

近年来我国高速铁路建设发展迅速。由于东北地区特殊的气候条件，该区域的高速铁路建设面临着较为复杂的季节性冻土路基冻胀融沉问题[1-2]，使铁路路基产生变形，引起轨道不平顺。主要是由于地温的变化影响导致。张玉芝等[3]基于哈大高速铁路3 a的现场监测数据和气温资料，研究路基地温随时间的变化特点和沿深度的分布规律，并预测地温场的变化趋势。工程上从各个层面采取了多种措施以控制路基变形[4-5]，如在冻深范围内采用防冻胀填料换填，在路基面采取防水封闭措施，设置保温层和防冻胀护道等。许健等[6-8]研究了保温、换填等防冻胀措施可能对路基地温场造成的影响，研究了加铺防冻胀护道对冻结深度的影响。上述措施取得了积极的治理效果，但仍存在一定的局限。由于无砟轨道路基上覆盖的轨道板对路基起到一定的保温作用，而路肩处覆盖较少；路基两侧太阳辐射情况不同，东坡受到的辐射要强于西坡，即存在阴阳坡效应[3]。上述两点原因，使路基在横向上产生地温差异，从而可能引起横向变形差异，造成轨道水平不平顺。研究学者[9-12]采用数值模拟方法分析了多年冻土区和季节冻土区路基保温护道的效果。基于此，本文基于监测断面实测数据，拟合初始值及边界条件，运用有限元软件COMSOL Multiphysics建立3种不同型式的防冻胀护道的路基模型并开展计算。研究不同型式防冻胀护道对路基冻结特征的影响，分析了其对路基横向地温及横向冻深差异的消除效果。

1 计算模型

1.1 模型建立及计算

1.1.1 温度控制方程

如果路基土体在冻结过程中不受外部力荷载，不计地基土体蒸发耗热，热量对流和水分迁移，根据能量守恒定律和傅立叶定律，可建立热传导微分方程如下

(1)

引入温度控制方程焓法[13]形式，用来考虑冰水相变作用

(2)

式中，ρ为材料密度；c为材料比热；λ为材料的热传导系数；T为温度；t为时间；H为焓。

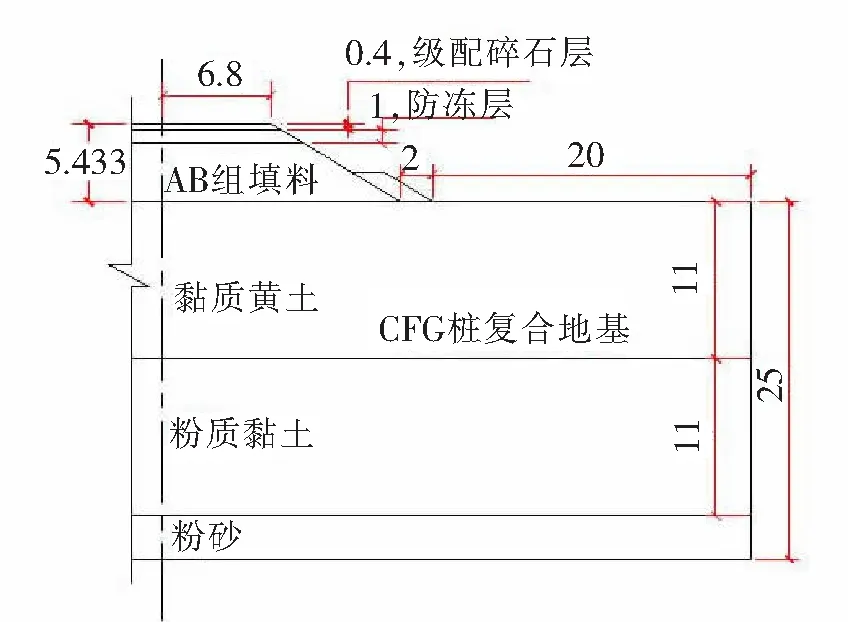
图1 路基断面结构(单位：m)

1.1.2 计算模型建立、边界条件及参数确定

路基断面结构见图1。Dirichlet(狄氏)边界条件是将边界条件确定为常数，或具体随时间变化的温度函数，又称基本边界条件。采用狄氏边界条件的方法，边界条件取值引用张玉芝等研究成果[3]。

通过实测数据的分析可得，级配碎石层，AB填料层，黏质黄土层存在季节性冻融；粉质黏土层，粉砂层常年处于不冻状态。在建立计算模型的过程中，存在相变的材料采用式(2)温度控制方程焓法形式，需输入焓和导热系数；始终处于单一物态的材料可采用式(1)温度控制方程基本形式，需输入密度、比热和导热系数。由于冻结深度在路基高度范围内，更加关注的是路基范围的温度场，地基为CFG桩加固的土体，其导热系数和比热容参数与黏质黄土等存在一定差异，但由于加固后的地基实际热学性质可能需要一段时间才能稳定，计算过程中统一按照黏质黄土等土体的热学参数选取，对浅层土体的温度场影响并不显著。根据文献[3]和文献[13]，材料热学参数如表1～表4所示。

表1 材料的密度 kg/m3

表2 材料的比热 J/(kg·℃)

表3 材料的导热系数 W/(m·K)

网格划分采用自由剖分三角形网格，共划分4 840个三角形单元。将相应参数输入，先进行稳态计算一次，再进行瞬态计算[14]。瞬态计算起点为2010年8月1日，总时间取30 a，步长为24 h。

1.2 不同型式防冻胀护道的设置

护道的材料选用AB填料，为探究不同护道型式对路基冻深及横向冻深差异的影响，在实测断面的基础上改变断面护道的几何尺寸，新增了2种路基防冻胀护道型式。

(1)维持护道宽度2 m不变，将两侧护道高度由2 m统一升高为3.7 m，如图2所示。为方便表述，下文将称此种护道型式为“3.7 m对称型护道”。

表4 材料的焓 106J/m3

(2)维持护道宽度、东侧护道高度2 m不变，将西侧护道高度升高至与路基顶面齐平，达到5.433 m，如图3所示。下文将称此种护道型式为“5.433 m非对称型护道”。

此外，为方便进行比较，将实测断面护道型式(两侧护道宽和高各2 m)称为“2.0 m对称型护道”。

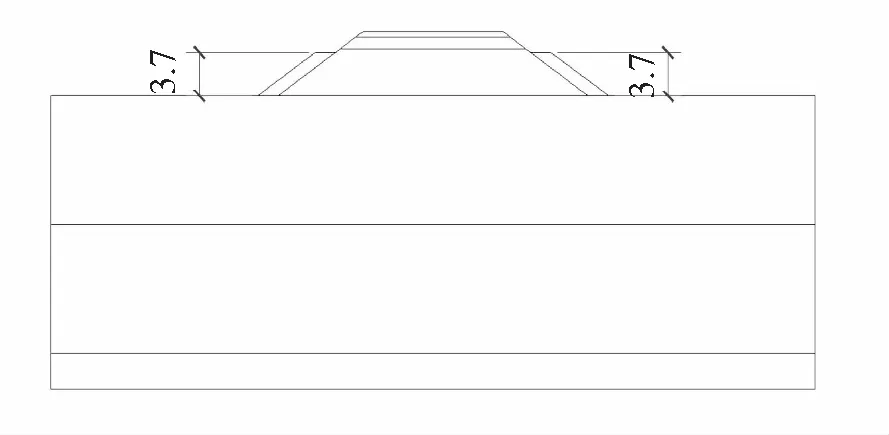
图2 3.7 m对称型护道(单位：m)

图3 5.433 m非对称型护道(单位：m)

2 数值计算结果及分析

2.1 模型验证

路基断面为DK883+330，测点选东路肩、西路肩和线路中心处距路基顶面以下0.8 m，2010年8月1日—2013年8月1日的实测地温值与模型模拟值进行比较，比较结果见图4。从图中可以看出模拟值与实测数据基本上比较吻合，有相同的变化规律，所以选用的该模型及参数和边界条件的取值是合理的，温度场的计算结果是可以利用的。

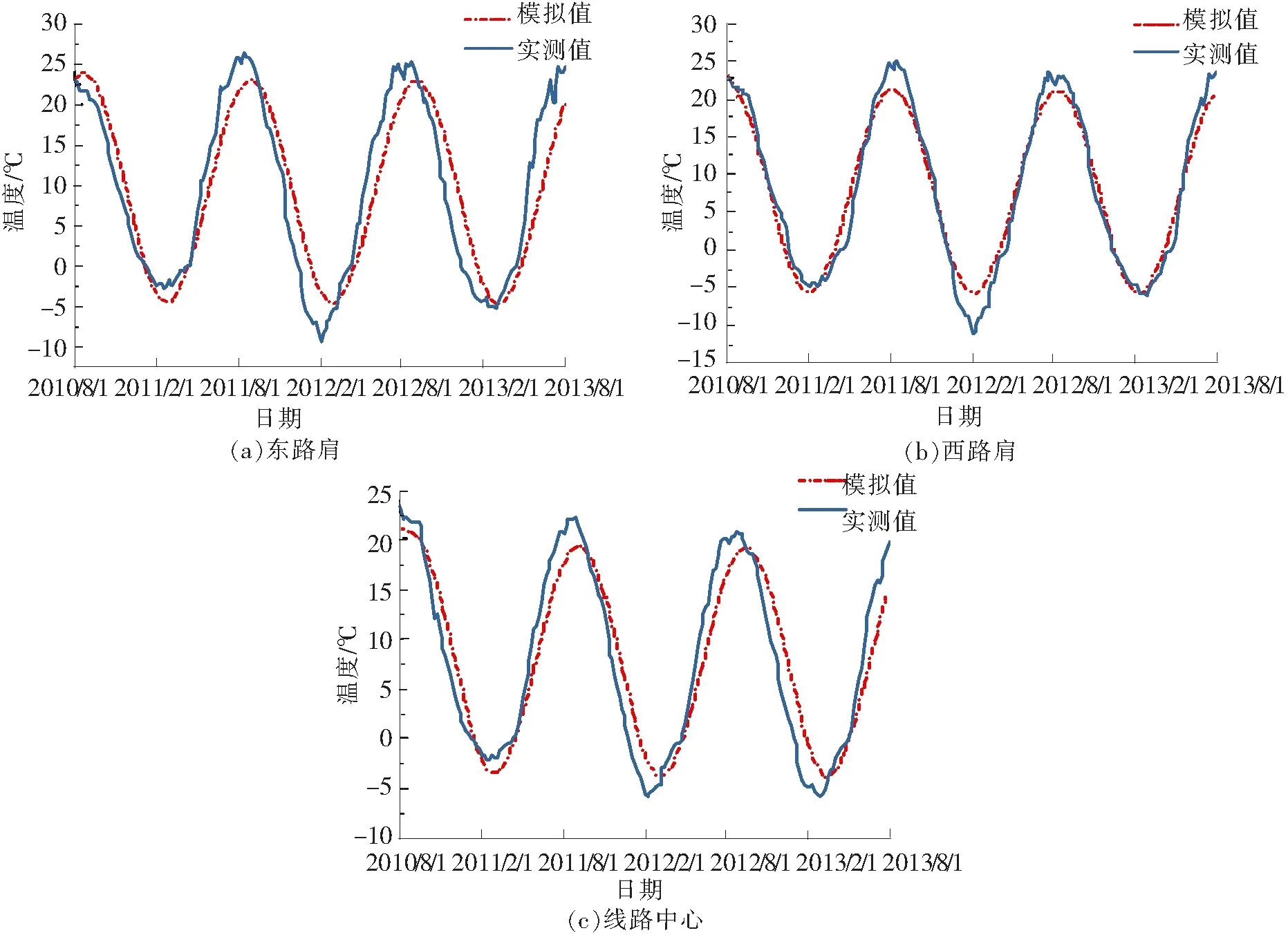
图4 路基顶面以下0.8 m处地温实测值与模拟值的比较

2.2 温度场稳定年限分析

由于路基填土具有较大热阻，且该断面所属路基填筑时间为2010年8月，外界温度接近年最高气温，路基和地基土体内积蓄了较多的热量，因此在修建路基后，地基土内原有热学平衡被打破，路基和地基土体需要一定时间来达到新的热学平衡。

图5 2.0 m对称型护道温度变化曲线

取东西路肩及线路中心测孔路基顶面以下5.8 m处测点，绘制30 a间测点的温度变化曲线。2.0 m对称型护道路基在线路中心-5.8 m的温度变化曲线见图5，其它2种型式的路基各测点的温度变化曲线规律和结果一样。

经过计算，观察3组曲线可知，由于考虑了气候变暖因素，引用了地温增温率系数[15]，约10 a后地温的平衡位置开始呈稳定升高趋势，可知此时热力平衡已经形成。

2.3 地温时程曲线

通过比较3种不同型式路基不同位置、不同深度处的地温时程曲线，研究不同型式护道对路基地温的影响以及对横向温度差异的消除效果。图6和图7分别为3种型式路基在路基面以下0.8 m(记作-0.8 m)及路基面以下2.8 m(记作-2.8 m)深度东西路肩处地温随时间的变化曲线。平均地温及其差异的具体值见表5。

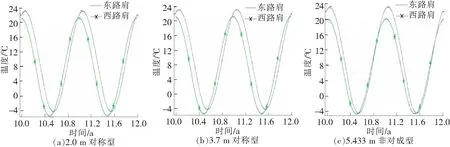
图6 不同型式护道-0.8 m处地温时程曲线

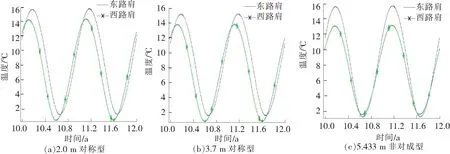
图7 不同型式护道-2.8 m处地温时程曲线

表5 平均地温和温度差异具体值 ℃

由图6、图7和表5可得出以下结论。

(1)继续采用对称型式，将护道高度提升到3.7 m对东西路肩位置-0.8 m及-2.8 m处的平均地温及地温横向差异几乎没有影响；增大防冻胀护道高度会稍稍降低路基的平均地温。

(2)采用非对称型式护道，阳坡侧护道高度不变，将阴坡侧护道高度提高到与路基同高反而会增大地温差异，但不显著，增幅约为0.1。

2.4 最大冻深比较

建模时为减小边界条件对计算的影响，现取线路中心两侧25 m，天然地面以下10 m的范围作为分析讨论的对象。由2.2节得，10 a后路基温度场达到稳定，现研究第11年内(2020年8月1日—2021年8月1日)典型时刻路基温度场，包括开始冻结时刻及冻深达到最大时刻。

以西路肩开始冻结作为路基冻结的起点。根据模拟结果，对比3种型式路基第11年内不同时刻的冻深，可得3种型式路基开始冻结的时刻均为2020年11月24日；达到最大冻深的时刻分别为：2.0 m对称型2021年3月1日，3.7 m对称型2021年3月6日，5.433 m非对称型2021年3月11日。

3种护道型式路基最大冻深的对比见图8，具体冻深值见表6，东西路肩的冻深差异取绝对值。

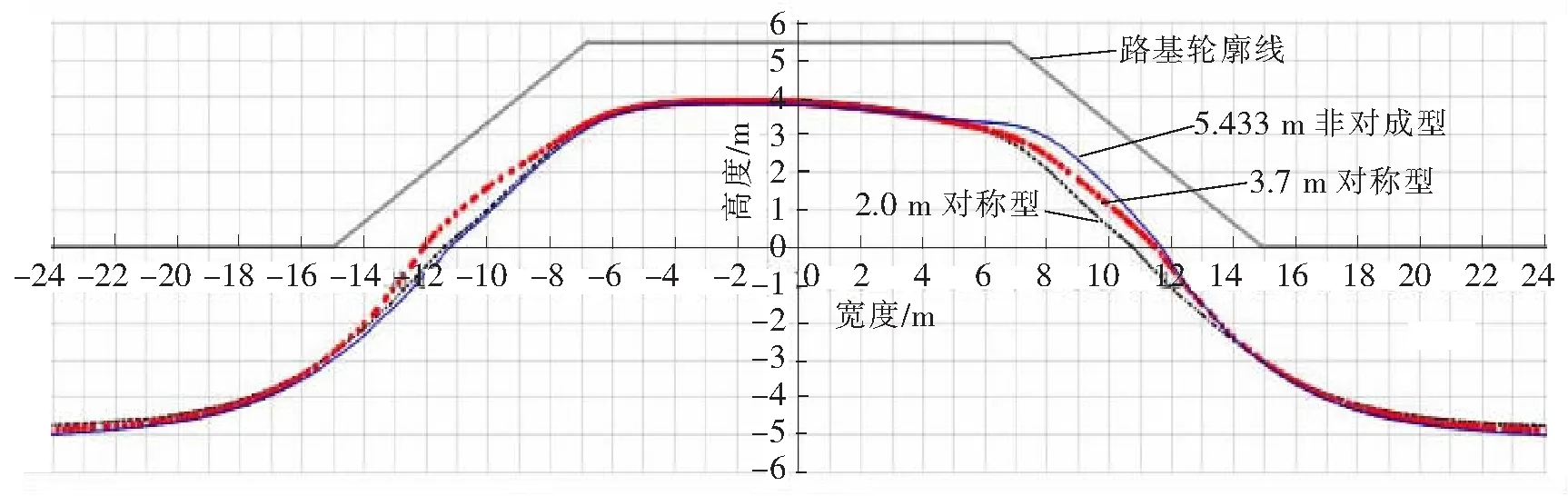
图8 3种型式护道的最大冻深对比

(1)从减小冻深的角度看，2种新型式护道的保温效果均优于现有2.0 m对称型护道。

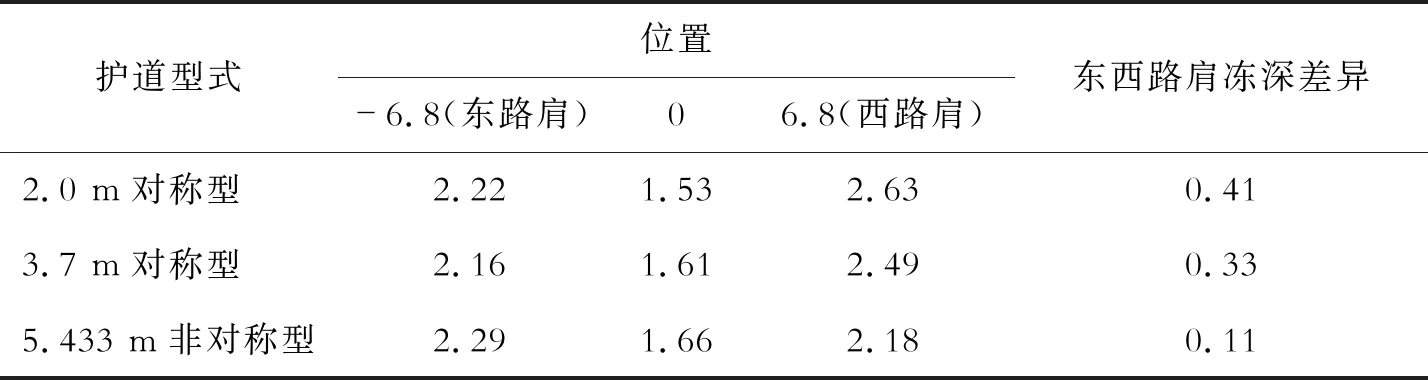
表6 3种型式路基冻深值比较 m

(2)3.7 m对称型、5.433 m非对称型同2.0 m对称型相比，增加的材料用量大体相同，且二者均能在增加了护道高度后在一定的影响范围内有效减小冻深。但从减小路基横向地温差异的角度考虑，仅增强西侧护道的5.433 m非对称型优于3.7 m对称型。

2.5 讨论

对数值模拟的计算结果进行了后处理，3种不同型式防冻胀护道对路基东西路肩平均地温，横向温度差异，最大冻深及最大冻深差异的影响进行了比较分析。不同型式的防冻胀护道对东西路肩位置-0.8 m及-2.8 m处的平均地温及地温横向差异影响非常小；在路基横向冻深差异的问题上，5.433 m非对称型设计对横向冻深差异的消除效果明显，较之于两种对称设计更有优势，根据现阶段研究成果，建议在修建类似季节性冻土区高速铁路路基南北走向时采用东侧较低，西侧较高，且西侧高度与路基齐平的非对称型式护道，以最大限度减小路基冻深及横向冻深差异。下一步需要做的是，如何有效调整防冻护道的型式使得横向地温和横向冻深差异最小。