粒子群优化算法在匈牙利水汽层析中的应用研究
2019-09-23严宇翔胡伍生
严宇翔,胡伍生
(东南大学 交通学院,江苏 南京 211189)
在大气层当中,对流层中的水汽,扮演着很多重要的角色。所以对水汽的监测,显得尤其重要。与传统的水汽监测手段不同,全球卫星导航定位系统(GNSS)能够提供24 h、全天候的观测[1-2]。GNSS观测值受对流层中水汽的影响,在信号接收的过程中,会产生一个湿延迟[3-4]。不少学者研究了利用GNSS信号湿延迟对水汽进行三维重建的技术[5-7]。例如,王维等[5]根据上海地区GPS综合应用网,研究了代数重构技术中的3种算法,即ART、MART和SIRT,实验结果表明,这3种重构算法具有可行性,而且收敛较快,结果比较可靠。何林等[6]采用香港SatRef的观测数据,对Kaczmarz算法及其变种,共8种常见的代数重构算法进行了对比分析,实验发现,效果最好的是CAV算法,再者是Cimmino算法,另外验证了松弛因子的重要性。
以上算法都属于代数重构算法,需要设置合适的松弛因子,但是一般都是通过经验选取,设置方法很有技巧性。而粒子群算法是一种智能的优化算法[8],自适应强,能够自动搜索出最优的松弛因子,可以解决松弛因子凭经验选取的弊端。
本文的目的是利用层析技术来重建匈牙利地区水汽折射性(refractivity)的三维分布,因为水汽的折射性(refractivity)与水汽的密度密切相关[9-10]。本文提出利用粒子群优化算法选择松弛因子,根据匈牙利地区的GNSS 网络的数据进行层析实验,并用粒子群算法方法优化松弛因子解算层析方程,得到水汽折射性的三维分布,并与探空数据进行比对,验证方法的可行性。
1 对流层水汽层析原理
1.1 层析模型
有很多学者详细阐述了GNSS 对流层水汽层析的原理,本节的有关公式参考自文献[5-7]。
湿延迟的产生原因是对流层大气折射,定义为:
(1)
其中:nw是湿折射指数 (wet refractive index);Nw是湿折射性(wet refractivity)。
将式(1)离散化,用矩阵的形式表达,得到:
Ax=b.
(2)
其中:A为系数阵;x表示网格水汽密度;b为斜路径湿延迟的106倍。然而式(2)代表的线性方程是稀疏的,用一般的最小二乘算法无法解算。
1.2 层析解算算法
代数重构(ART)算法中,Kaczmarz算法是最为经典的算法之一[11]。Kaczmarz代数重构算法属于迭代算法,每一次迭代都包含有m步,每一步处理A中的一行射线。
代数重构(ART)算法原理:
(3)
其中,i代表第i行,x是用向量的形式表示的湿折射性;<·>代表向量的内积;λ是松弛因子。
粒子群优化(PSO)算法[12-14]的算式为:
(4)
(5)

(6)
PSO优化松弛因子层析算法步骤如下:
第1步:初始化m个粒子;
第2步:粒子状态的第一次更新, 根据式(4)和式(5);
第3步:根据式(6)计算粒子群中个体的适应度值 , 得到个体最优与群体最优位置;
第4步:根据式(4)和式(5),对粒子状态进行更新;
第5步:重复第3步;
第6步:达到迭代终止条件,获得最优松弛因子λ;
第7步:将松弛因子代入式(3),进行层析解算;
第8步:获得水汽折射性三维分布。
本文把传统的代数重构算法记作ART算法,把粒子群优化的代数重构算法记作PSOART算法。
2 数据
2.1 数据获得
实验数据采用根据匈牙利地区GNSS网络,由区域数值天气模型 (ALADIN/AROME模型)生成的虚拟斜路径延迟(SWD)数据[15-16]。数据时间为2017-09-11, 6~12 UTC。实验的这个时段,恰逢中欧地区的一段暴雨天气。一共生成了579条有效SWD射线。图1描述了GNSS站点的分布情况。利用匈牙利的两个城市Budapest和Szeged的探空站数据,为层析解算提供初始值和验证值。探空气球的发射时间分别是在2017-09-11的0:00 和 12:00。
2.2 数据处理
格网的划分情况如图1所示。
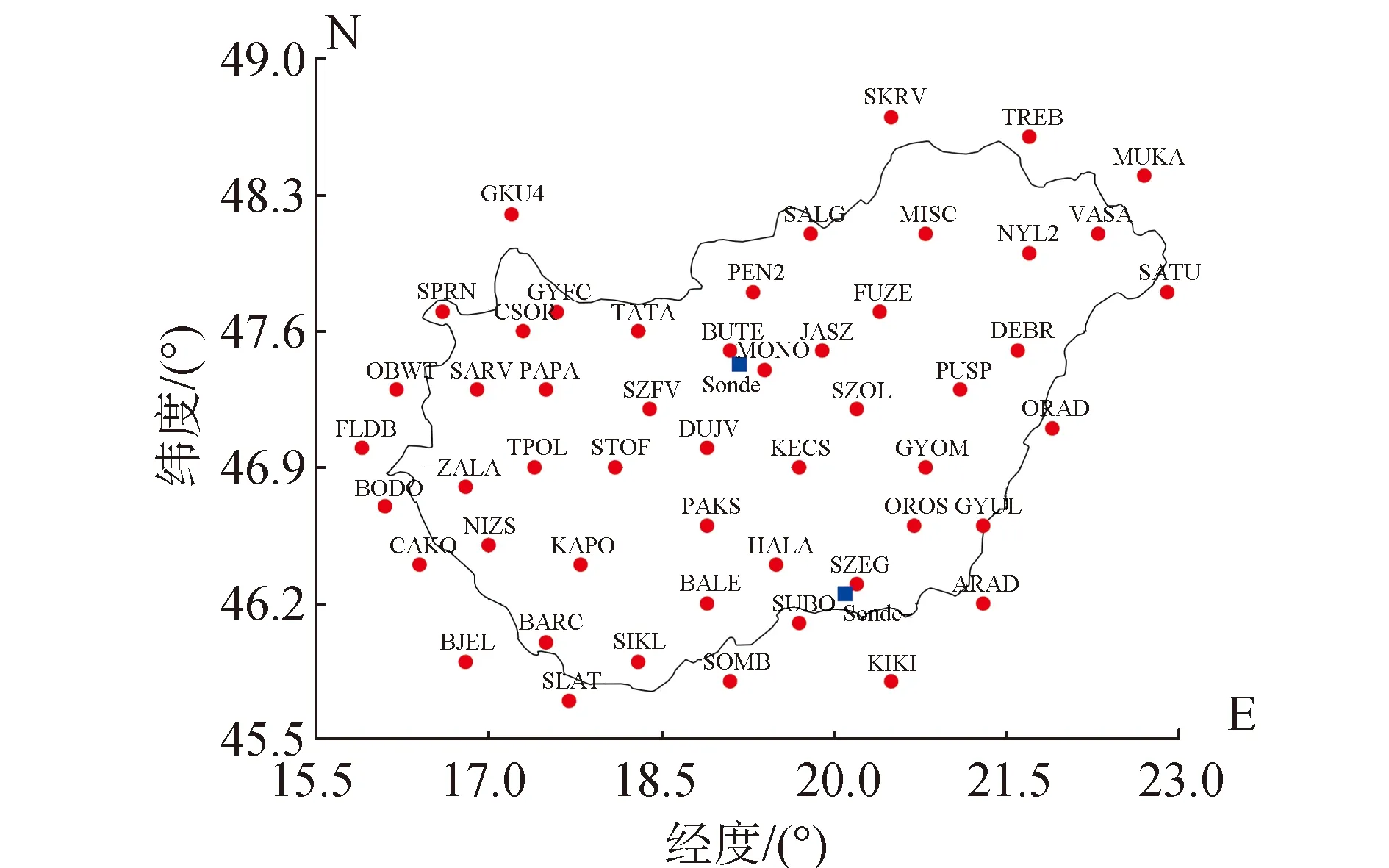
图1 格网的平面图
坐标系统的建立和三维格网的参数如下:原点:45.5° N, 15.5° E, 0 m;最大边界:49.0° N, 23.0° E, 12 000 m;X轴正方向:north;Y轴正方向:east;Z轴正方向:up;纬度方向格子长度:皆为0.7°;经度方向格子长度:皆为1.5°;垂直方向格子长度:1 000 m, 1 000 m, 1 000 m, 2 500 m, 2 500 m, 4 000 m;三维格网总格子数:5×5×6。
2.3 实验方法
本文分别采用传统的代数重构算法(ART)和粒子群优化的代数重构算法(PSOART)进行实验,并做对比研究。具体实验过程如下:
根据第1节中介绍的原理,构建三维水汽层析模型。Budapest 0:00的探空数据作为层析解算的初始值,实验中,GNSS信号射线的总数为579条,将其分为训练集和测试集两部分。训练集是利用其中450条来建立水汽层析模型,并采用粒子群算法优化松弛因子对层析方程进行解算,这450条射线的选择是随机的。剩下的GNSS信号射线作为测试集,用来对模型进行检验。另外,层析的结果也与Szeged®的探空数据进行了比较。
实验过程是用MATLAB编写的相关程序进行操作,其中利用了代数重构的相关工具包[11]。程序运行了多次。因为用来建立水汽层析模型的450条射线是随机选择的,所以每次程序的运行结果都有小差异,但十分地稳定。本文在第3节中,对其中一次的层析实验结果进行了展示。
3 结果分析
层析重建水汽三维分布的结果如图2所示,图中展示的是每一层的水汽折射性(refractivity)。
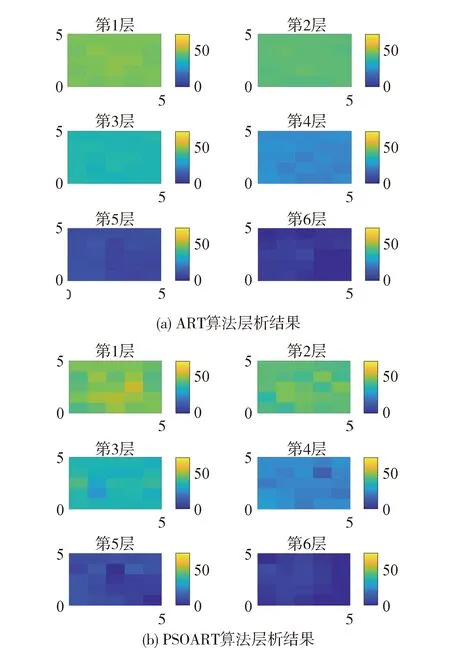
图2 水汽折射性三维分布
其中,PSOART算法中,应用PSO优化松弛因子的过程如图3所示。当迭代终止时,获得最优的适应度值,并得到此时对应的松弛因子,λ= 0.290 8。

图3 松弛因子优化过程
粒子群优化算法是一种随机搜索方法,图3显示,当达到迭代终止条件时,迭代次数为60,可见计算效率较高。
为了验证层析模型的精度,对根据层析模型重建的射线SWD值和原始的射线SWD值进行了残差分析。图4展示了残差序列的情况。其中包括训练集和测试集的结果两部分。
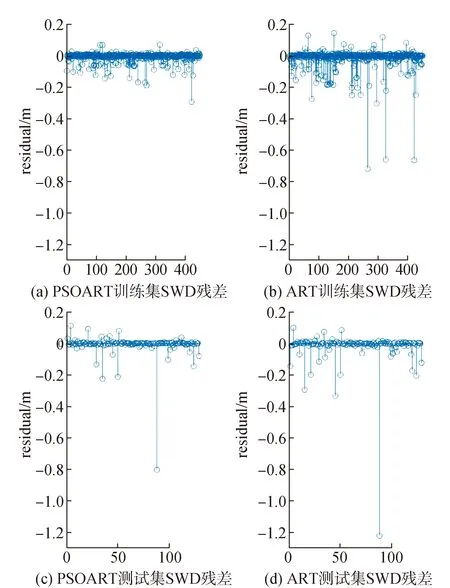
图4 原始SWD与模型重建SWD 的残差分析
结果表明,层析PSOART算法的残差序列整体比ART的要好,说明PSOART算法重建的SWD与原始的 SWD吻合度更好。另外,给出层析重建相对误差的计算结果,如表1所示。
相对误差的计算公式为:
(7)

表1 层析重建SWD的相对误差
结果表明,采用ART的层析结果,训练集和测试集的平均相对误差分别为2.2%和2.3%。而PSOART的训练集和测试集的平均相对误差分别为1.5%和1.6%,精度得到明显提升,验证了本文算法的可靠性。
本实验还将层析结果与探空的数据进行了比较。因为Budapest的探空数据被用来作为初始值,于是用Szeged的探空数据与层析结果进行验证。由于只获得了0:00 UTC和12:00 UTC时刻的探空数据,并没有获得9:00 UTC的探空数据,因此将层析结果与这两个时刻分别进行了比较。
图5表明Szeged地区的GNSS水汽层析结果与探空数据的吻合情况,可以看到无论是ART还是PSOART,层析重建的水汽折射性廓线与0:00的探空廓线,吻合度良好,与12:00的探空廓线有些许偏离,验证本文算法的可靠性。

图5 层析与探空的廓线比较
4 结 论
水汽在气象研究中有很多重要的应用。本文使用层析技术重建了匈牙利地区的三维水汽分布。分别比较了传统的ART算法和本文提出的用PSO优化松弛因子的PSOART算法。通过匈牙利地区的GNSS网络进行层析实验,实验结果表明,无论是平均相对误差,还是回归方程,PSOART算法的结果都要优于传统的ART算法。因此可知,使用粒子群优化的水汽层析是可行的,相比传统的ART算法,精度得到明显的提高,并且算法智能,自适应性强。
