淤地坝淤积对漫顶溃坝洪水影响数值模拟研究

张兆安， 侯精明， 刘占衍， 马利平， 李占斌， 李小纲

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室， 陕西 西安 710048；2.河北省邯郸水文水资源勘测局， 河北 邯郸 056006)

1 研究背景

为了治理黄土高原严重的水土流失问题，淤地坝作为最有效的防治水土流失的沟道工程措施[1]，在我国黄河流域被大量建造并使用[2]，它能够防洪拦沙、淤地增产、充分利用水沙资源和改善生态环境[3]，通过抬高沟底侵蚀基准面，提高了流域斜坡稳定性，减少了沟坡重力侵蚀发生的可能性[4]。但在实际运行中，随着淤地坝淤积高度变高，漫顶溃坝问题变得越来越频发。由于气候变化，我国极端降雨导致的致灾暴雨事件增加[5]，仅在1994年，陕北就有7347座淤地坝在暴雨中被摧毁[6]。因此，研究淤地坝溃坝洪水的影响具有十分重大的意义。

近年来我国西北淤地坝事故频发，国内关于淤地坝的研究日渐增多，王保勤[7]分析了渗水在淤地坝灾害中的危害，在淤地坝设计施工等方面提出建议；魏霞等[6]认为从长时间尺度、大范围来看水毁不是件坏事，淤地坝灾害防治研究对淤地坝的建设有着重要意义，肯定了对淤地坝水毁溃坝的研究；许五弟等[8]按照不同的暴雨洪水和库容状态对淤地坝进行了模拟分析，验证了淤地坝溃坝预报预警地理信息模型应用的可行性，但没有直观体现淤地坝的溃坝规律；王乃欣等[9]利用虚拟现实软件，在地形不变的情况下改变初始水位，对淤地坝溃决进行仿真研究，使淤地坝溃坝结果更加直观，但并未研究淤积高度对于淤地坝溃坝的影响；高海东等[10]用SINMAP模型定量评估了淤地坝淤积高度对斜坡稳定性的影响，研究了淤地坝淤积至不同高度时的斜坡稳定性，为淤地坝建设提供参考。但以上对于淤地坝灾害的研究都缺乏对淤地坝淤积高度与其溃坝洪水关系的研究。

为研究不同运行周期淤积高度改变下溃坝洪水特征的变化规律，本文采用耦合了溃口演变过程的二维水动力模型，模拟了淤积高度分别为20%、40%、60%、80%坝高情形下的淤地坝漫顶溃决及下游洪水演进过程，分析了淤积高度对溃坝洪水峰值的量化影响。研究成果可用于指导淤地坝运行维护及防洪减灾工作。

2 研究方法

本文采用考虑溃口演变过程的DB-IWHR模型计算溃口演变下的溃口处流量过程，并使用溃坝洪水演进模型(GAST模型)计算下游洪水演进过程，溃坝过程模拟流程见图1。

图1 溃坝过程模拟流程图

GAST模型即显卡加速的地表水及其伴随输移过程模型(GPU Accelerated Surface Water Flow and Transport Model (GAST))，该模型基于Godunov的有限体积法求解二维浅水方程，该方法可以稳定地解决不连续问题，严格保持物质守恒，应用二阶算法提高了模拟的计算效率和精度。它还耦合并模拟模型中浅水流动的一些其他物理化学反应，如沉积物和污染物运输。该模型的另一个特征就是使用GPU计算来提高计算性能。

2.1 溃坝洪水演进模型控制方程

平面二维浅水方程(SWEs)又称圣维南方程，被广泛用于模拟自然河流、湖泊和沿海地区的浅水流动，同时它还可以描述溃坝问题。二维浅水方程可以写成：

(1)

其中变量矢量、不同方向上的通量矢量以及源项矢量可以表示如下：

(2)

式中：q为变量矢量，包括水深h， m；qx和qy为x、y方向的单宽流量，m3/s；F和G分别为x、y方向的通量矢量;g为重力加速度，m3/s；u和v分别为x、y方向的流速，m3/s；S为源项矢量；zb为河床底面高程，m；Cf=gn2/h1/3为谢才系数，m1/2/s。

2.2 溃坝洪水演进模型数值方法

GAST模型采用Godunov格式的有限体积法对平面二维浅水方程进行求解。选用具有二阶时空精度的MUSCL型格式以初始水深来进行空间二阶精度的变量重组，以重组后的数值作为计算变量，使数值变量守恒。在控制单元内，界面上的物质与动量通量通过HLLC近似黎曼求解器计算[11]；通过静水重构来修正干湿边界处负水深；底坡源项用底坡通量法进行处理。摩阻源项(摩阻力)使用较为稳定的半隐式法计算，以此来提高稳定性[12]，并采用二阶显式Runge Kutta[13]方法进行时间步长的推进。

本模型模拟溃坝过程时，采用GPU并行计算技术实现高速运算[14]，以此来提高模型计算效率，但模型未考虑溃坝时的土动力过程。

2.3 溃口演变模型

本文使用DB-IWHR模型(DB模型)来模拟考虑溃口演变的情况下的溃口流量过程。DB模型由中国水利水电科学研究院开发，考虑了溃口断面的流量会受到水流在垂直方向冲刷影响，也会受到侧向扩展影响的问题[15]。由于下游河床很低，溃口出口水流按自由出流考虑，这时溃口断面流量可用宽顶堰公式计算[16]：

Q=CB(H-z)3/2

(3)

式中：Q为流量，m3/s；B为断面宽度，m；H为库水位，m；z为进口处河床高程，m；C为综合流量系数，经验取值为1.4 m1/2/s[16]。

关于冲刷计算，DB-IWHR模型提出一种双曲型侵蚀率模型，认为水流冲刷土石料时，土石料抵抗冲刷侵蚀的能力并非是无限制的[15]。关于溃口扩展计算，模型采用简化Bishop[17]法自动搜索临界圆弧滑裂面，对溃口扩展进行分析，相关原理和计算方法在文献[18]中有详细说明，本文不再赘述。

该耦合模型在文献[19]中模拟计算实际溃坝洪水已经得到验证。

3 淤积高度对溃坝洪水影响模拟

为研究不同运行周期淤积高度改变下溃坝洪水特征的变化规律，本文采用耦合了溃口演变过程的二维水动力模型，分别对矩形沟道、王茂沟某淤地坝模拟其淤积高度为20%、40%、60%、80%坝高情形下淤地坝漫顶溃决及下游洪水演进过程，其中矩形沟道及王茂沟某淤地坝坝高皆为10 m，并结合实际工程淤地坝坝高，将模拟坝高提升至20、30 m进行模拟，对所得结论进行一般性地拓展。

3.1 矩形沟道淤地坝溃决洪水过程模拟

为了研究淤积高度对溃坝洪水的影响，本文设计一个1 000 m×200 m的矩形沟道，以左下角作为零点，在x正方向795～800 m处为淤地坝(图2)。

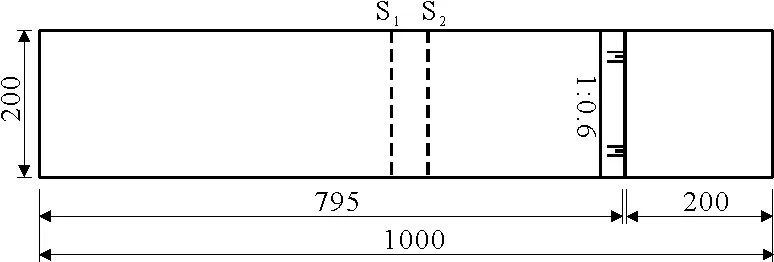
图2 矩形沟道示意图(单位：m)

3.1.1 矩形沟道溃坝方案 本文设定淤地坝坝高10 m，坝宽和坝长为5和200 m。坝体下游是一个坡面，坡度取1∶0.6。在漫顶的条件下，对不同淤积高度的淤地坝进行溃坝模拟，并在下游截取代表断面(图2中以S1、S2表示)进行研究。

3.1.2 DB-IWHR模型参数设置 用DB-IWHR模型建立溃口关系并计算溃口流量，再通过GAST模型计算下游河道洪水演进过程，设定曼宁系数为0.025[20]，下游为自由出流开边界，其余为闭边界，参考DB模型使用说明书及相关文献[21]，设定参数如表1所示。

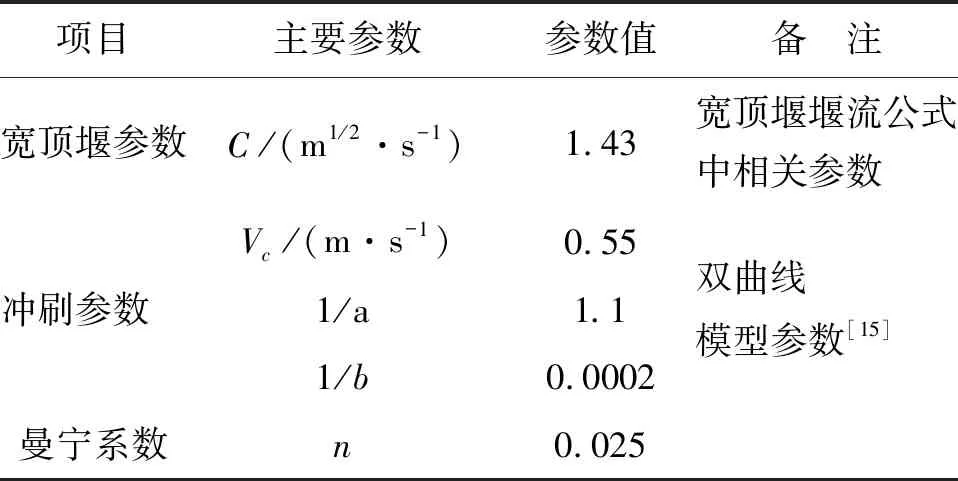
表1 DB-IWHR模型参数设定

设定入库流量Qin=0，保持初始水位H0=10 m始终不变。库容—水位关系满足以下方程：

dw=(Qn-Qin)dt

(4)

dH=dw/(200×200)

(5)

式中： dw为水量，m3； dH为水位，m; dt为时间步长，s;Qn为流量，m3/s。

3.1.3 矩形沟道溃坝模拟结果 图3和4分别为矩形沟道在库区淤积高度不同的情况下，下游代表断面的溃坝洪水流量过程线，以及两断面处洪峰流量与淤积高度拟合曲线(此处取均方根误差最小的二次多项式拟合)。由图3、4可以看出，洪峰流量随淤积高度的增加而下降，且下降趋势逐渐变缓。其中，S1处二次多项式均方根误差为1.92 m3/s，相关系数为0.999；S2处二次多项式均方根误差为2.87 m3/s，相关系数为0.999。

表2为不同淤积高度下代表断面的洪峰流量及洪峰流量削减率表，淤积高度至20%时，两断面的洪峰流量削减率增加至44.4%左右；淤积高度至40%时，两断面洪峰流量削减率增加至72.0%左右，故洪峰流量随淤积高度的增加而减小，洪峰流量削减率随淤积高度增大而增大。

3.2 王茂沟某淤地坝溃决过程模拟

3.2.1 研究区域概况 王茂沟位于陕西省榆林市绥德县，是韭园沟流域的一个分支，流域面积5.97 km2，其中沟间地占58.4%；沟谷地占41.6%，主沟长3.75 m[22]。自1953年开始综合治理后，建造淤地坝40多座，已拦泥超150×104m3，在沟内已经形成较完整的坝系[23]。

根据激光雷达扫描技术获取生成的1 m精度数字地形高程文件，选择一处典型小支沟，溃口完好，垂直于下游水流流向截取两个代表断面D1、D2，研究区支沟地形及代表断面位置如图5所示。

表2 代表断面洪峰流量及洪峰流量削减率

3.2.2 王茂沟溃坝洪水过程模拟结果 对王茂沟淤地坝地形及相关参数做类似矩形河道的处理，下游为自由出流开边界，其余为闭边界，在坝后的库区内，设定初始水位始终为10 m水位，不随淤积高度发生改变。模拟使用了高精度实际地形，经过模拟可以得到三维展示图(图6)及计算结果。

图7、8分别为王茂沟淤地坝在库区淤积高度不同的情况下，下游代表断面的溃坝洪水流量过程线，以及代表断面处洪峰流量与淤积高度拟合曲线，得到洪峰流量与淤积高度可用二次多项式进行拟合。由图8可看出，洪峰流量随淤积高度的增加而下降，且下降趋势逐渐变缓。其中，D1处二次多项式均方根误差7.359 m3/s，相关系数为0.995；D2处二次多项式均方根误差6.686 m3/s，相关系数为0.996。表3为代表断面不同淤积高度下的洪峰流量及洪峰流量削减率，淤积高度至20%时，两断面的洪峰流量削减率增加至48.2%左右；淤积高度至40%时，两断面洪峰流量削减率增加至74.0%左右，故可得出实际淤地坝地形与矩形沟道相似的结论。

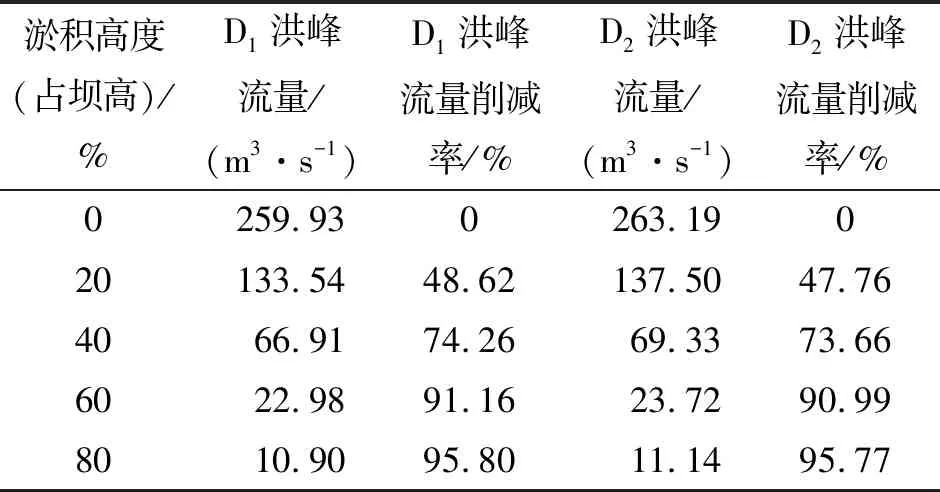
表3 代表断面洪峰流量及洪峰流量削减率表

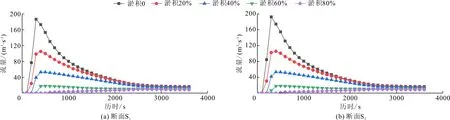
图3 代表断面处溃坝洪水流量过程线

图4 代表断面处洪峰流量与淤积高度拟合曲线

图5 研究区域地形及代表断面位置图

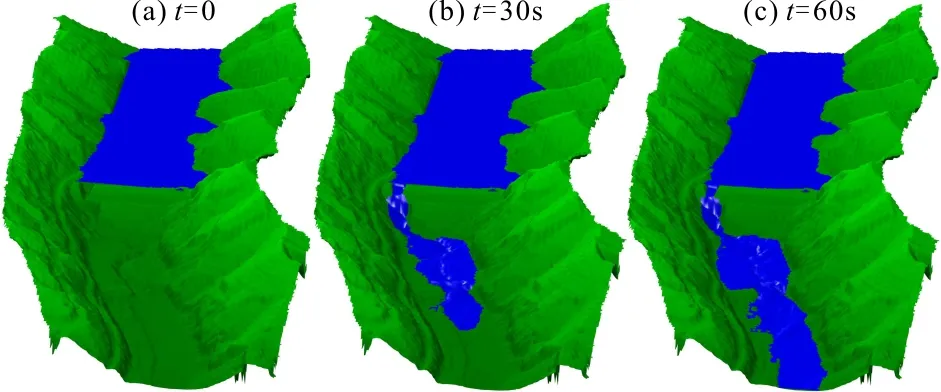
图6 溃坝洪水演进三维展示图

3.3 不同坝高下的淤积程度对溃坝洪水过程影响模拟

由以上分析得出，当淤地坝坝高为10m时，在各个算例中均得到统一的溃坝洪水演变规律，故本文再次计算理想沟道地形条件下坝高为20和30 m的情形，淤积高度每次增加量为淤地坝坝高的20%，结果如下：

图9、10分别为不同坝高的情况下，下游代表断面D1的溃坝洪水流量过程线，以及代表断面D1处洪峰流量与淤积高度拟合曲线。可得出与10 m坝高时类似的结论，坝高20 m时二次多项式均方根误差为4.641 m3/s，相关系数为0.999；坝高30 m时二次多项式均方根误差为16.435 m3/s，相关系数为0.998。

表4为不同坝高的情况下，代表断面D1不同淤积高度下的洪峰流量及洪峰流量削减率，淤积高度增至坝高的20%时，两种坝高的洪峰流量削减率平均增加至34.7%左右；淤积高度至40%时，两种坝高洪峰流量削减率平均增加至64.4%左右。得到结论与坝高为10 m时类似，即洪峰流量随淤积高度的增加而减小，洪峰流量削减率随淤积高度增大而增大。

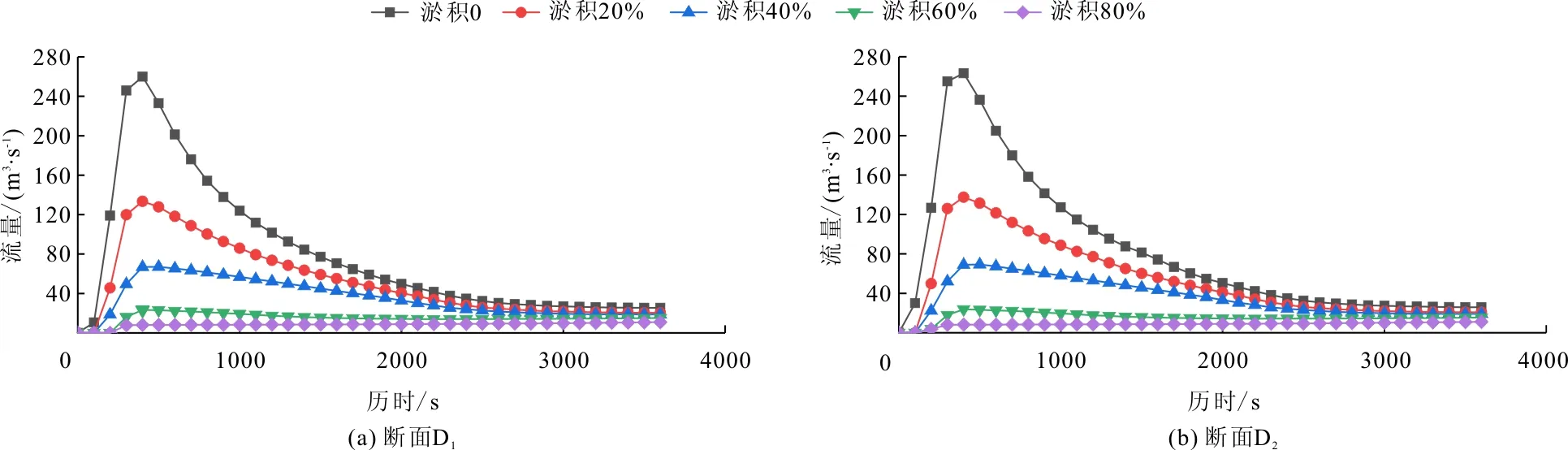
图7 代表断面处溃坝洪水流量过程线

图8 代表断面处洪峰流量与淤积高度拟合曲线

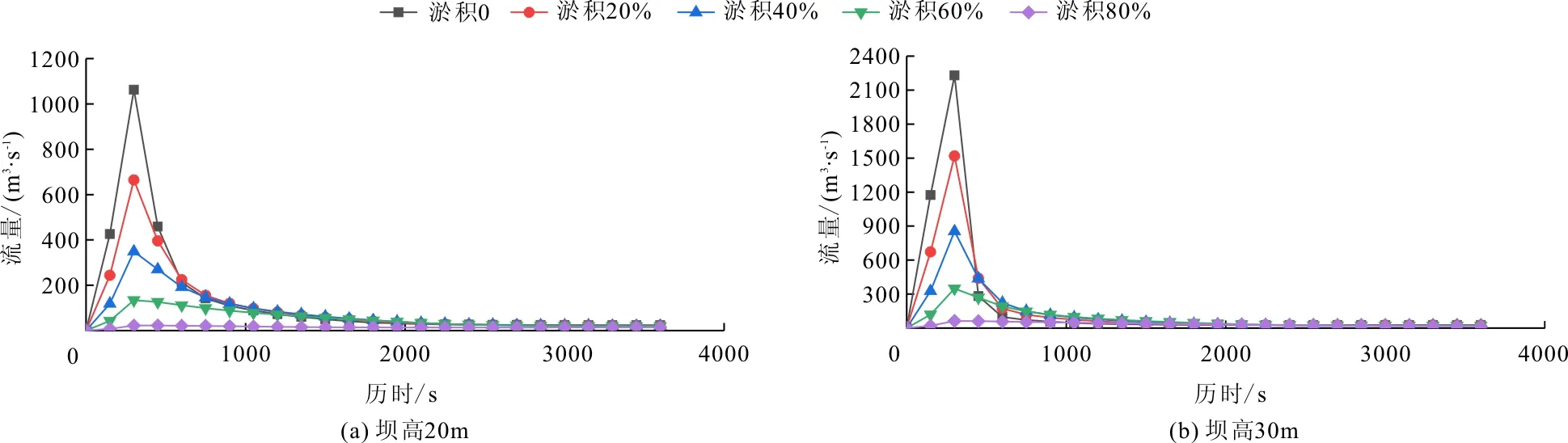
图9 不同坝高代表断面D1处溃坝流量过程线

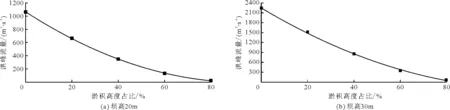
图10 不同坝高代表断面D1处洪峰流量与淤积高度拟合曲线

表4 代表断面D1洪峰流量及洪峰流量削减率表

4 结 论

为研究不同运行周期淤地坝淤积高度改变下漫顶溃坝洪水特征的变化规律，本文对不同淤积高度下的淤地坝溃坝洪水进行数值模拟研究，结论如下：

(1)淤地坝溃坝洪峰流量随淤积高度增加而减小，并可用二次多项式拟合，相关系数均在0.99左右，拟合精度较高，研究成果对淤地坝溃坝灾害预报有一定意义。

(2)在淤地坝淤积初期和中期，淤积高度对于溃坝洪水影响较大，淤积高度至坝高20%和40%时，平均洪峰流量削减率分别达40.50%和68.71%，淤地坝淤积对于降低溃坝洪水灾害影响效果显著。

(3)本文采用考虑了溃口演变的水动力模型，分别模拟计算了在不同地形、不同坝高情形下不同淤积高度淤地坝漫顶溃决及下游洪水演进过程，分析了淤地坝淤积对溃坝洪水的影响，各算例得到的规律一致，建议在淤地坝建坝完成初期(淤地厚度在坝高20%左右)加强对于溃坝灾害的预防措施。

本文研究了不同运行周期淤积高度改变下溃坝洪水特征的变化规律，为淤地坝建设、维护及防洪减灾提供了理论依据。本次研究未考虑泥沙输移，水库来流等因素对溃坝洪水的影响以及管涌溃坝的情形，将在未来研究中加入未考虑因素，使结果更加合理。