山区河流溃坝洪水演进分析

2019-09-23董嘉锐李占斌刘基兴朱战齐

水资源与水工程学报 2019年4期

王雯，董嘉锐，杨杰，李鹏，李占斌，刘基兴，朱战齐

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西西安 710048; 2.大唐陕西发电有限公司石泉水力发电厂，陕西石泉 725200)

1 研究背景

山区洪水具有流速急，水量集中，突发性强的特点。一直以来，山洪灾害对世界上诸多山地国家的公共安全和社经济发展构成巨大威胁[1]；山区又是建造大坝的天然基地，我国各类水库数量从新中国成立前的1 200多座，增加到98 000多座，已形成初步的防洪减灾工程体系，当坝体存在溃坝风险时，突发的溃坝洪水造成的安全威胁不可忽视。

针对溃坝后的洪水演进过程，周兴波等[2]基于溃口扩展模型和一维潜水波模型对白格堰塞湖溃决洪水进行了分析和对比，为堰塞湖应急处置提供了参考。马利平等[3]通过集成 HLLC 近似黎曼求解器的二维水动力模型，对支沟溃坝洪水进行了模拟，说明支沟溃坝洪水对主河道行洪具有一定影响。杨志等[4]通过耦合模型对黑河金盆水库溃坝过程进行了模拟，结果表明，耦合模型可提高模型计算的准确性。王晓玲等[5]通过三维水动力模型，对东武仕水库溃坝洪水演进进行了数值模拟，并将传统的坝区附近模拟范围扩大到下游城市建筑群整体范围。这些研究均侧重于溃决下泄流量过程[6]，数值计算方法[7-8]以及洪水波演进[9-10]等方面，由于山区河流蜿蜒曲折，有明显的区间汇流现象，河道宽窄变化，边界条件复杂，目前对于长距离山区河流溃坝洪水演进的过程及相关问题研究尚显不足。鉴于此，本文以石泉大坝至喜河大坝段40 km长度河道为模拟对象，通过拟定大坝溃口形状及溃坝时刻，获得溃坝下泄流量过程线，建立区段平面二维计算模型，对典型山区型河道溃坝洪水演进过程进行了模拟，为防洪规划和调洪决策提供依据。

2 数学模型及数值求解方法

2.1 平面二维洪水演进数学模型

本文基于不可压缩Reynolds值均布的Navier-Stokes方程，满足Boussinesq假定和静水压力假定，建立洪水演进模型。

二维非恒定浅水方程组[11]为：

(1)

(2)

(3)

式中：t为时间，s；h=η+d为总水深，m，其中d为静止水深； m、η为水面高度，m；u,v分别为x,y方向速度分量，m/s；f为柯氏力系数，f=2ωsinφ，其中ω为自转角速度、φ为纬度；g为重力加速度，m/s2；ρ为水的密度，kg/m3；sxx、sxy、syy分别为辐射应力通量；Txx、Txy、Tyx、Tyy为黏滞应力项;S为源项矢量;us,vs为源项流速。

(4)

水平黏滞应力Tij的表达式为：

(5)

在空间上对控制方程采用非结构化网格有限体积法离散，可保证连续性方程和动量方程的守恒；采用显性欧拉法对时间进行离散。

模型基本方程可表示为如下形式：

(6)

式中：U为守恒型物理向量；F为通量向量；S为源项；I为无黏性通量;V为黏性通量。

2.2 模型参数

计算河段划分采用非结构三角形网格，采用动边界处理技术[12]处理干湿边界。河道糙率反映了计算河段的形态变化、边界条件等因素的综合影响，计算所采用的河道糙率主要由实测水流资料率定确定，分段、分高程对河道糙率进行了调整，使得5年一遇及20年一遇洪水模拟条件下的水位与实测水位偏差小于1%，调整后河道糙率范围为0.020～0.035。水平涡黏系数采用Smagorinsky公式计算，模型中采用值为0.28。垂向涡黏系数采用对数定律公式计算。

3 溃坝洪水演进过程模拟

3.1 溃坝方案及流量确定

石泉大坝主坝坝型为混凝土空腹重力坝，最大坝高65 m，坝顶长度353 m，坝基岩石为石英片岩。坝体从左至右编号：1～3坝段为左岸非溢流坝段，4～6坝段为厂房坝段，7～23坝段为泄洪、排沙、溢流坝段，24～29坝段为右岸非溢流坝段。

本次计算采用瞬时溃坝模式，根据大坝安全监测及运行管理人员建议，溃坝范围拟定为8～23坝段，溃坝缺口底部高程拟定为387 m，溃口宽度为170.5 m，溃口深度控制为29 m；另一方案为非溢流坝段溃决，溃口宽度为52 m，溃口控制深度为39 m，深度到达坝体建基面。溃决时刻为库区水位达到拟定溃坝水位时刻，此时库区来流为入库洪水(设计洪水位410.29 m，校核洪水位413.67 m)。最大下泄流量采用宁利中等[13]提出的解析解求得，叠加入库洪水及库容计算溃坝下泄流量过程线，计算结果见图1。计算工况见表1。

3.2 研究区域及网格划分

二维数学模型计算河段总长约40 km，起于石泉水库大坝，上至城关镇，途经石泉县城、池河镇、后柳镇、上至城关镇，喜河镇，老喜河镇、下至喜河水电站，见图2。计算区域地形数据根据区段河道带状1∶1000地形图进行构建，局部地区采用实测断面数据进行修正，计算网格节点数125 006个，网格单元数235 905个。为了尽可能准确的反映区域流场，对河岸及模型边界处网格进行加密处理，计算区域局部河段网格分布见图3。

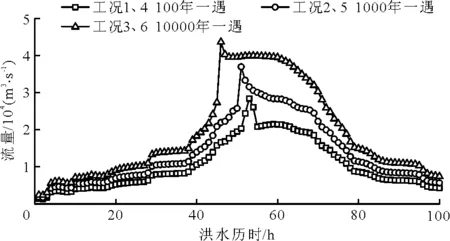
图1 各工况溃坝下泄流量过程线

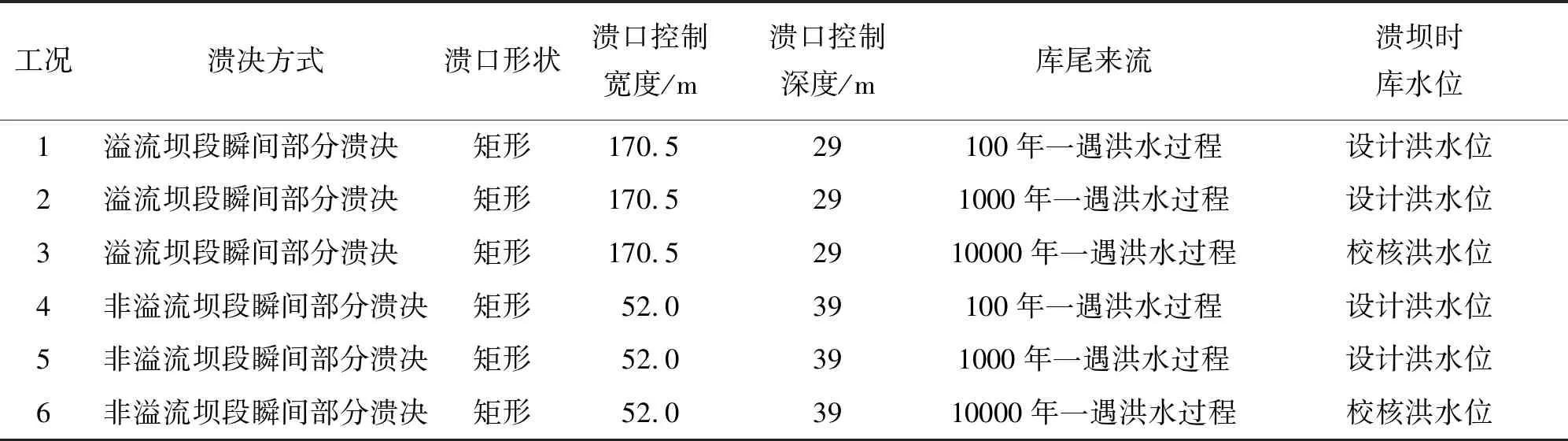
表1 各工况计算参数

图2 计算范围水系图及重点防护对象分布图

图3 研究区域局部网格结构图

3.3 结果分析

3.3.1 溃坝洪水演进过程溃坝洪水演进的关键研究内容之一是洪峰的传播到达时间，精确掌握溃坝洪水到达时间，可有效进行防洪预警，减少洪水损失。工况2和6的特征断面平均流速随时间变化图见图4和5。由图4、5可看出，溢流坝段溃坝时，由于溃坝增加流量相对正常泄洪流量较小，下游特征断面流速增大不显著；当非溢流坝段溃坝，断面越靠近大坝，流速峰值越明显，溃坝发生于洪水过程第45 h，石泉大坝下游G210线石泉汉江大桥处断面平均流速可达5.28 m/s，但由于石泉县城段河道顺直且河宽较宽，坝体下游5 km处河道自然束窄且形成弯道，为一天然卡口河道，坝体至弯道间形成滞洪区，弯道后十天高速以及安阳铁路汉江6号桥河段流速增大较为平缓，断面平均流速峰值相比溃坝下游1 km范围内削减明显。由各断面峰值出现的时间可获得溃坝传播过程，溃坝水流在研究区域整体传播时长为43 min，由于河道支流汇入较多，且大洪水条件下主流河水倒灌入支流，迟滞并削减了洪峰向下游的传播。

3.3.2 水位特征分析选取具有代表性的石泉县城城区段河道进行说明，图6、7分别为工况1、工况2溃坝发生40 min时洪水水位分布图。工况1最高水位为378.0 m，工况2最高水位为382.0 m，高水位均位于饶峰河与汉江交汇口左岸区域。主要原因为：石泉大坝泄洪水流顶冲点位于该部位，部分水流动能转化为势能，并逐渐向两侧扩散；下泄洪水在饶峰河河口形成逆时针环流，环流顶托饶峰河支流水位，并在支流形成倒灌；石泉县城段下游河道急剧束窄，并形成弯道，弯道凹岸顶冲点水位明显抬升，并在弯段下游逐渐降低，石泉县城段溃坝产生的洪水波波峰在经过下游弯道卡口段后被削减。

图4工况2特征断面溃坝洪水流速随时间变化过程图5工况6特征断面溃坝洪水流速随时间变化过程

图6工况1溃坝后40min石泉县城洪水水位分布图图7工况2溃坝后40min石泉县城洪水水位分布图

图8、9分别为工况2溃坝发生40、43 min计算区域水位分布图。图8与9表明，由于石泉大坝下游11 km处池河汇入，池河汇入方向与汉江主河道正交，且交汇口位于汉江弯段左岸凹岸，一方面使得溃坝洪水流量倒灌池河，另一方面顶冲点处山体严重顶托下泄洪水，壅高上游段汉江河道水位及池河水位。计算模型整体分析，由于山区河道的弯曲和不规则形态，洪水演进沿程阻力大，受边界条件影响显著，使得溃坝洪峰在传播过程中迅速坦化，对下游喜河电站影响作用逐渐减小，表明河道的蜿蜒能够很好地降低远处的受灾。

3.3.3 流速分布以工况2为例进行整体分析，工况2溃坝发生40 min计算区域流速分布见图10。

由图10可看出，溃坝发生后大坝下游河道流速迅速增加，但由于河流较长、弯道众多且主河道两侧存在有支流及支毛沟，溃坝洪峰流量及能量在传播过程中由于支流倒灌以及交汇口处的环流消耗水量及能量，使洪峰流量过程逐渐坦化，水流流速减小。除溃口段水流流速较大外，其余河段并无出现6 m/s以上断面平均流速，各工况河段最大流速介于4～6 m/s之间。

以老喜河镇段河道为例，工况5溃坝发生40 min老喜河镇段河道洪水流速矢量分布如图11。此河段洪水由于支流与主流间产生众多的扩散回流区，支沟水流与主流进行动量交换，削减主流能量，但水流横向切割冲刷岸坡，可能导致边滩、河岸崩塌，河道拓宽，应注意重点位置处的防护。局部河段两岸束窄处岸坡存在有突出的陡峭岩体，造成岸坡段形成较高的流速值，由图11可见，局部流速可达5 m/s。