基于Budyko假设的黄河下游非一致性径流模拟

2019-09-23丛培月牟献友冀鸿兰张宝森

水资源与水工程学报 2019年4期

丛培月，牟献友，冀鸿兰，张宝森

(1.内蒙古农业大学水利与土木建筑工程学院，内蒙古呼和浩特 010018； 2.黄河水利委员会黄河水利科学研究院，河南郑州 450003)

1 研究背景

黄河是我国第二大河流，多年平均径流量为580×108m3，约占全国总径流量的2%[1]。 2014年，IPCC全球气候变化第五次评估报告显示：全球气候变暖已被广泛认可，变暖体现在地表温度上升、极端气候事件频率增加等方面，1880-2012年全球平均温度已升高0.85℃，气候变化的严重性远超于以往的认知[2]。气候变化会改变降水及蒸散发，造成水文气象序列出现非一致性[3]。水文气象的非一致性会影响陆地水循环过程，驱动径流量的变化[4]。由于历史资料的缺失，黄河径流量演化规律的分析和判别将受到一定的限制[5]，因此，流域径流关系演变分析、径流模拟应运而生，成为当前水文水资源领域研究的前沿与热点之一，也是国际上一个具有挑战性的问题[6]。

近50年来，黄河径流量较以往有着显著差异，国内外许多学者针对中国各江河流域的径流模拟，进行了定量分析研究[7-8]。顾朝军等[9]分析了黄河陕县站1919-1997年天然径流量变化，指出黄河天然径流量年际变化存在明显的阶段性及周期性特征；王雁等[10]通过对径流和气象观测数据的统计分析，发现黄河流域由于气候变化引起了径流量的减少。张建云等[11]提出，自20世纪70年代以来，受气候变化的影响，黄河中游河川径流呈现明显的下降趋势。孙福宝等[12]基于Budyko假设的傅报璞公式检验了干旱区水热耦合理论。熊立华[13]分析了Budyko假设在中国南部湿润地区的适用性，并提出Budyko公式改进方法，提高了径流模拟精度。张丽梅等[14]利用Budyko假设分析渭河年径流量变化特征。对径流的模拟大多是基于水文气象序列概率分布及其参数随时间不变的假定[15]，张波等[16]指出，在环境变化的大背景下，一致性假设的水文理论无法精准地揭示水资源演变规律，在此背景下提出了非一致性年径流模拟方法，使结果更加真实、可靠；唐雄朋等[17]探讨了雅鲁藏布江拉孜以上流域非一致性径流过程模拟与预测，径流模拟精度较高；邓晓宇等[18]对气候变化和人类活动综合影响下的抚河流域进行径流模拟研究，发现纳西系数达到0.82以上。Milly等[19]指出，在气候变化和人类活动的影响下，年径流序列通常是非一致性的，导致许多现有方法径流模拟的精度较低；Merz等[20]根据奥地利273个盆地41 a的历史数据，通过校准模型参数来进行非一致性径流模拟，提高了径流模拟精度；Pathiraja等[21]通过使用集合卡尔曼滤波器同时估计模型参数，对西澳大利亚实验区进行径流预测，得出预测结果可被接受。

目前，对基于Budyko公式改进的Zhang模型在黄河下游流域的适用性研究尚有空缺。本文利用灰色关联法[22]与滑动样本熵等方法对黄河下游水文气象序列进行非一致性识别，将改进的Zhang模型应用于黄河下游，研究其在非一致性水文气象序列中模拟径流的适用性。

2 资料与方法

2.1 研究区概况

河南郑州桃花峪以下的黄河河段为黄河下游，地处中国东部，流经河南、山东，于山东垦利县注入渤海。黄河下游段位于东经110°～120°、北纬30°～40°之间，河长约786 km，为典型游荡型河段，河道宽浅，流域面积约2.3×104km2，占全流域面积的3%左右，总落差93.6 m，平均比降0.12%。黄河下游属于温带季风气候，夏季高温多雨(夏季季平均降水量为371.76 mm，夏季季平均气温为26.39℃)，冬季寒冷干燥(冬季季平均降水量为56.71 mm，冬季季平均气温为1.34℃)，多年平均降雨量约617.52 mm，年内降水分布不均，多年平均气温约14.49℃，多年平均径流量约253.45×108m3，多年平均日照时数约2 548.77 h。根据降雨径流分带，大部分为半湿润地带。

2.2 数据来源

收集了黄河下游 7 个水文站(花园口、夹河滩、高村、孙口、艾山、泺口、利津)1979-2015年共37 a的逐日降雨、逐日气温、逐日流量等水文资料以及周边4个气象站(郑州、开封、济南、惠民)的1979-2015年逐日日照时数等气象资料，数据均来源于黄河流域历年水文年鉴、中国气象数据网(http://data.cma.cn)。

2.3 研究方法

本文利用灰色关联法分析径流复杂现象与降水、气温发展态势的关联、接近的程度，从而确定径流形成的主控因素。由于水文气象序列的非一致性会直接影响降水和潜在蒸散量，造成气候-径流关系的方式不同于过去的观察[23]，因此在非一致性水文气象序列下，选用基于历史经验的水文模型将影响模拟精度。本文首先进行水文气象序列的一致性验证，利用累积距平法和滑动平均法进行初步检验，并基于滑动样本熵法[24]进行突变分析，联合多种分析方法对水文气象一致性进行诊断。由于实际蒸发量难以通过观测直接获得，通常利用潜在蒸散发量来计算实际蒸发量[25]，本文采用在湿润与半湿润区优先选择的Hargreaves[26]法估算潜在蒸发量，通过潜在蒸发量利用Budyko假设计算蒸发量，最后利用水量平衡法反算径流量。

2.3.1 Budyko假设 Budyko(1974年)假设基本原理是：假定流域内降水和潜在蒸散发量决定了多年平均蒸散发，蒸散发量为降水与潜在蒸散发量之间的函数，即可以对降水、潜在蒸散发和径流之间定量关系进行较好的拟合[27]。但是由于植被类别、土壤水力特性及地形的区别，使得Budyko假设的广泛性受到限制，Zhang等在Budyko基础上引进模型参数ω，改进了Budyko假设公式。

Budyko假设可简单表达为：

(1)

(2)

Zhang公式：

(3)

式中：E为年平均蒸发量，mm；P为年平均降水量，mm；ω为植被水分利用系数；F为干燥指数；E0为年平均潜在蒸散发量，mm。

水量平衡法：

R=P-E

(4)

式中：R为径流深，mm；P为降水量，mm；E为蒸发量，mm。

2.3.2 模拟精度分析本文采用纳西系数(NSE)对年径流量的模拟精度进行评价。NSE∈(-∞,1)，其中当NSE=1时，模拟精度最优；NSE∈(0.01,1)时，模拟精度为可接受。

(5)

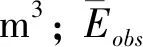
3 结果与分析

3.1 降水、气温与径流灰色关联度

以黄河下游7个水文站为代表站，设定降雨径流灰色关联度为γ1，气温径流灰色关联度为γ2。通过计算得出1979-2015年7个水文站的γ1、γ2，如表1所示。7个站的γ1、γ2均大于0.5，表示径流量与降水和气温关联度较高，即气温和降水均为黄河下游径流量的主控因素。此结果与张国宏等[28]的研究结论相似，黄河流域径流量与气温和降水均有较好的相关性，其中各站均为γ2>γ1，表明在黄河下游径流形成过程中，气温与径流量的关联度较大，对径流的影响所占的权重大于降水。

表1 1979-2015年降水、气温与径流的灰色关联度

3.2 降水、气温变化趋势分析

表2为1979-2015年黄河下游7个水文站的降水与气温突变年份。由表2可知，1979-2015年黄河下游流域降水和气温突变点不一致，如夹河滩站降水时间序列发生突变的时间为1999年，气温时间序列发生突变的时间为1993年；突变时间均在20世纪90年代前后，水文气象时间序列突变时间具有较高的同步性。本文以花园口站降水、气温变化趋势分析为例，其余6个站不再赘述。

表2 1979-2015年黄河下游7个站降水与气温突变年份

黄河下游1979-2015年间多年平均降水量为617.52 mm，降水量总体偏少。由线性拟合结果(图1(a))，降水量倾向率为-4.5 mm/10a，呈显著性减少趋势(p<0.05)，其中降水量最大值出现在1983年(962.94 mm)，最小值出现在1997年(368.96 mm)，极值比1.61。从降水量累积距平曲线(图1(b))可以看出：花园口站在1979-2015年间降水量变化呈现出先波动下降、后波动上升的趋势，即降水量变化分为两个阶段：第1阶段1979-2002年，该时期降水量平均值为596.24 mm；第2阶段2003-2015年，该时期降水量平均值为639.39 mm，第1阶段到第2阶段的变化呈现了降水枯-丰转变的过程，表明降水时间序列已发生变化。

1979-2015年，花园口站多年平均气温为15.14℃，年平均气温倾向率为0.6℃/10a。由线性拟合(图2(a))可看出，花园口1979-2015年38 a的年平均气温呈现显著上升趋势(p<0.05)。其中最高值和最低值分别出现在2015和1984年，分别为16.67和13.68℃，极值比为0.22。与降水量的变化相比，气温的变化较为平缓。从图2(b)的累积距平曲线可以看出，花园口站年平均气温表现出先下降后上升的发展趋势，自1997年起，花园口站气温开始由低温期向高温期过渡，表明气温时间序列也已发生变化。

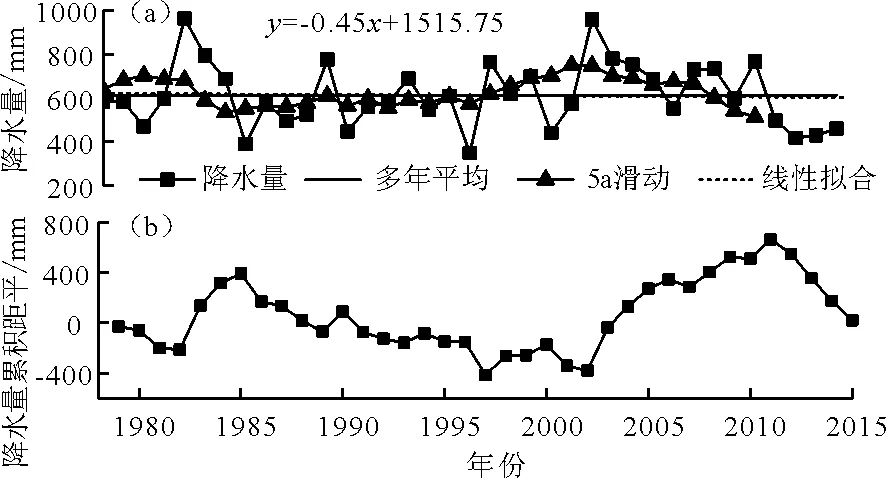
图1 花园口站1979-2015年年降水量时间序列变化趋势

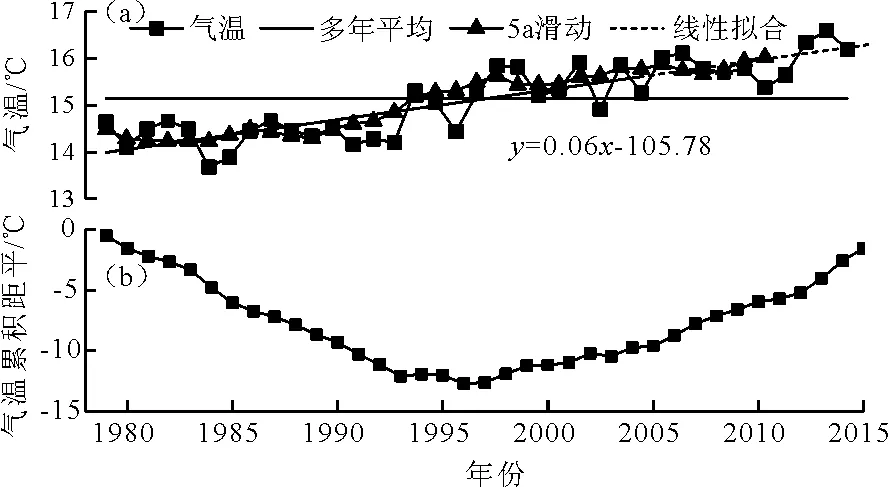
图2 花园口站1979-2015年年均气温时间序列变化趋势

降水量的滑动样本熵(SampEn)呈现逐渐增加的趋势(图3(a))，降水量变化分为3个阶段：第1阶段(1979-1986年)、第2阶段(1987-1993年)、第3阶段(1994-2015年)，即发生了两次突变，对应的突变点年份分别为1986和1993年，突变点前后的SampEn序列差异性显著。气温的SampEn值在0.6～0.9之间(图3(b)，其变化也呈现出3个阶段：第1阶段(1979-1991年)、第2阶段(1992-1994年)、第3阶段(1995-2015年)，对应的突变点年份分别为1991和1994年，气温时间序列的SampEn值均大于降水量序列，表明气温系统的复杂程度高于降水系统。

图3 花园口站1979-2015年年降水量、气温时间序列SampEn分析

整体而言，从发生突变的年份来看，年降水量和年平均气温发生突变的时间有较高的对应关系。由以上水文序列发生突变可知，水文序列的统计规律并非一致，因此水文序列不满足一致性。非一致性在径流、降水和气温中已被广泛认定。

3.3 潜在蒸散发量估算

利用Hargreaves方法在黄河下游4个水文站点(花园口、夹河滩、艾山、利津)中进行潜在蒸散发量估算，估算结果见图4。从图4可知，具有相似的规律特征，年平均潜在蒸散发量从850～1 200 mm不等，潜在蒸散发量均呈现随时间减少的显著趋势(p<0.05)，4个站点的气候倾向率分别为-20.8、-34.8、-76.3和-38.2 mm/10a，其中利津站在1990年前后出现了小幅回升，1979-1993年潜在蒸散发量呈现下降的趋势，气候倾向率为-34.60 mm/10a,2010-2014年潜在蒸散发量呈现上升的趋势，气候倾向率为51.79 mm/10a，这些变化符合近50年来中国潜在蒸散量的变化趋势[29]。

3.4 Budyko假设径流模拟精度分析

由于Budyko假设没有考虑人类活动和气候变化对径流量的影响，因此利用降水量与潜在蒸散发量，同时基于Budyko假设改进的Zhang模型求得蒸发量，通过水量平衡法反算径流量。本文以1982年为例，模拟计算了逐月径流量并与实测值进行对比，如图5所示。分析图5可知：花园口站在8月模拟结果误差最大(NSE<0)，在2月(NSE=0.81)和5月(NSE=0.97)模拟结果较为理想，夹河滩站和艾山站分别在7、8月模拟结果误差最大(NSE=0)，利津站在4月(NSE=0.97)、5月(NSE=0.99)、6月(NSE=0.86)模拟结果较为理想，模拟精度较高。表3给出了黄河下游4个典型区1982年月均径流模拟NSE检验结果，4个典型区的NSE均小于0。综合以上研究结果，在月尺度径流模拟中各个月模拟值与实测值之间误差较大，模拟精度过低，因此Zhang公式不适用于月尺度径流模拟中。

利用Zhang公式对4个水文站的1979-2015年径流过程进行模拟，结果如图6所示，模拟的径流变化过程与实际的径流变化过程基本吻合，能较好地反映径流的变化趋势和数值，但在2000年后个别年份模拟值与实际值差别较大，如花园口站2005年(NSE=-0.62)、2011年(NSE=-2.27)，艾山站2010年(NSE=-4.77)。但整体来看，4个典型区径流模拟的纳西系数均大于0.9(如表4所示)，说明模型精度较高，模拟结果可以接受，Zhang公式在年径流量模拟方面具有一定的适用性。

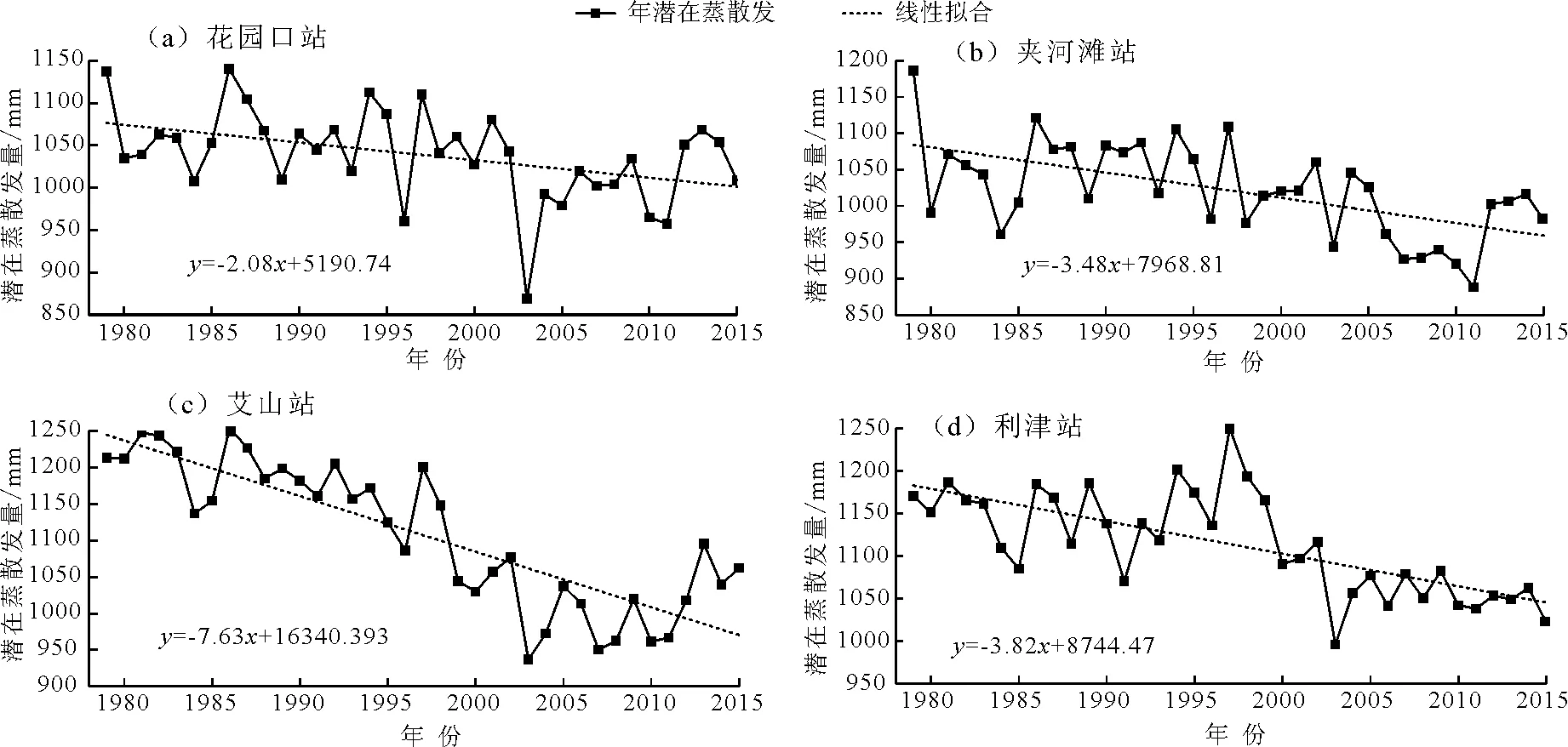
图4 黄河下游4个水文站1979-2015年潜在蒸散发量变化

图5 1982年黄河下游4个水文站月径流量观测值与模拟值变化分析

图6 1979-2015年黄河下游4个水文站年径流量观测值与模拟值变化分析

表3 1982年黄河下游4个水文站月径流量NSE对比

表4 1979-2015年黄河下游4个水文站年径流量NSE对比

径流量模拟的差异性受诸多因素影响，水文气象序列的选择、人类活动和气候变化等可直接影响径流量模拟精度。本文利用基于Budyko假设改进的Zhang模型对黄河下游进行径流量模拟，经过验证表明模型精度较高，适应于黄河下游流域非一致性水文气象序列的径流量模拟，可为黄河下游径流量分析、预报提供可靠的数据支持。