基于IPSO-SA算法的温室番茄产量预测方法

(浙江工业大学 机械工程学院，浙江 杭州 310014)

设施农业是现代农业的基础，而温室栽培是其重要组成部分，其中番茄以其广阔的市场前景和较大的需求，是温室中主要栽培蔬菜之一。以往温室种植者拥有的反季蔬菜提供能力使得其种植的温室蔬菜在市场上拥有较强的竞争力。然而近年来温室的数量逐渐增多，国外蔬菜的进口量越来越大，市场的竞争越来越激烈，用科学的方法对温室栽培的过程进行管理，增加温室栽培的经济效益成为在竞争中站稳脚跟的唯一方法。作物产量是温室生产中衡量经济效益的关键指标。因此，建立精确的番茄产量预测模型具有重要意义。

作物产量可以通过干物质分配模型计算，干物质分配模型主要有经验模型与机理模型。国内学者对经验模型的研究较多，倪纪恒等[1]利用累积辐热积拟合分配指数，并结合采收指数来预测温室番茄的产量。齐维强等[2]采用积温法研究温室番茄的生长发育模型。然而这类经验模型在建立温室番茄生长发育模型时主要依靠经验，缺乏机理性。国外相关的研究开展较早，目前能够较为准确地描述番茄生长的产量模型有TOMSIM(Tomato simulator)番茄生长发育动态模型[3]和Vanthoor模型[4]。这类机理模型能够模拟各器官的生长过程，描述作物的生长状态，如当前果实数量、叶面积指数及干物质分配比例等，同时还能够反映室内气候对番茄生长的影响，如温度、CO2含量和光照强度的影响。然而机理模型一般都有一个通用的缺点，虽然能够精确地模拟作物的生长过程，但是由于含有大量的作物生长状态，很多参数难以计算，在温室优化控制中无法直接使用。因此出现了简化TOMGRO(Tomato growth)番茄生长模型[5-6]。简化TOMGRO模型机理性强，在降低模型复杂度的同时还不失精确性，能够准确预测未来产量变化，但是在实际应用时需要根据实际种植环境对描述番茄生长状态的部分参数进行辨识[7]。参数辨识依据实验数据和所建立的模型，结合优化算法来确定模型中待辨识的参数，使模拟值最大程度上拟合实际值。鲁建厦等利用改进粒子群算法对混流混合车间生产调度问题[8]和装配线平衡[9]进行优化。王卫红等[10]提出PCA-FOA-SVR方法对股票价格进行预测。张娟等[11]运用RBF神经网络和遗传算法建立了番茄茎干的生长模型。文欢等[12]利用灰色神经网络模型对加工番茄产量进行预测。Vazquez-Cruz等[13]用遗传算法校准TOMGRO模型。然而神经网络模型需要采集大量数据进行训练，遗传算法中遗传操作参数的选择大部分依靠经验，算法搜索速度慢。因此需要一种快速精确的优化算法对简化TOMGRO模型进行参数辨识。结合PSO算法收敛快速[14]和SA算法不易陷入局部最优[15]的特性，笔者提出了IPSO-SA算法。通过分析算法求解待辨识参数的过程以及模型产量预测的精确度，比较PSO，SA和IPAO-SA算法的优劣，并得到适合本地种植条件的番茄产量预测模型，为温室番茄的生产提供参考。

1 材料与方法

1.1 试验材料

试验温室位于上海市崇明示范基地，主要用于栽培无限生长型番茄。温室控制系统自带的Priva气象站、CO2检测仪和光照传感器等仪器每5 min进行一次数据采集，对温室进行全方位监控[16]。无限生长型番茄单个果实质量不大，由于生产周期长，具有高产量的特点。根据崇明温室的种植经验，串番茄单果鲜重质量为100～200 g，根据一次收获的果实总产量和总数，可以估算出单果果实鲜重质量为160 g左右。番茄的生长周期总天数为300 d，集中育苗时间约为30 d，温室种植的时间约270 d，结合崇明温室实际的种植情况及已有数据，选择2015年9月30日—2016年5月12日(共32 周，224 d)为番茄在温室内的种植周期。Vanthoor模型是一种机理比较充分的番茄生长模型，能够比较精确地模拟番茄的生长发育过程，已经在欧洲和北美等地区得到了广泛验证。本研究使用的数据包括上海崇明试验温室2015—2017 年两个种植周期的室内温度数据、CO2浓度数据、光照强度数据和番茄生长数据，其中番茄幼苗移植到温室中时的初始数据如表1所示，番茄实际产量数据由Vanthoor模型仿真得到。

表1 温室番茄初始状态Table 1 Greenhouse tomato initial state

1.2 番茄产量预测模型构建方法

笔者采用机理模型与参数辨识方法[17]，建立番茄产量预测模型，构建方法如图1所示。番茄的生长模型采用简化TOMGRO模型，结合前人对TOMGRO模型的研究，提取模型中的待辨识参数，得到待辨识的番茄产量预测模型。将温室内的温度、CO2浓度、光照强度以及番茄实际产量数据输入待辨识的模型，通过比较模拟值与实际产量值，采用优化算法计算求解不确定参数。利用不同日期的室内外环境数据和产量值对优化后的番茄产量模型进行有效性校验，若模型验证合理则可用来预测番茄产量，否则重新进行上述步骤，直到模型验证合理。

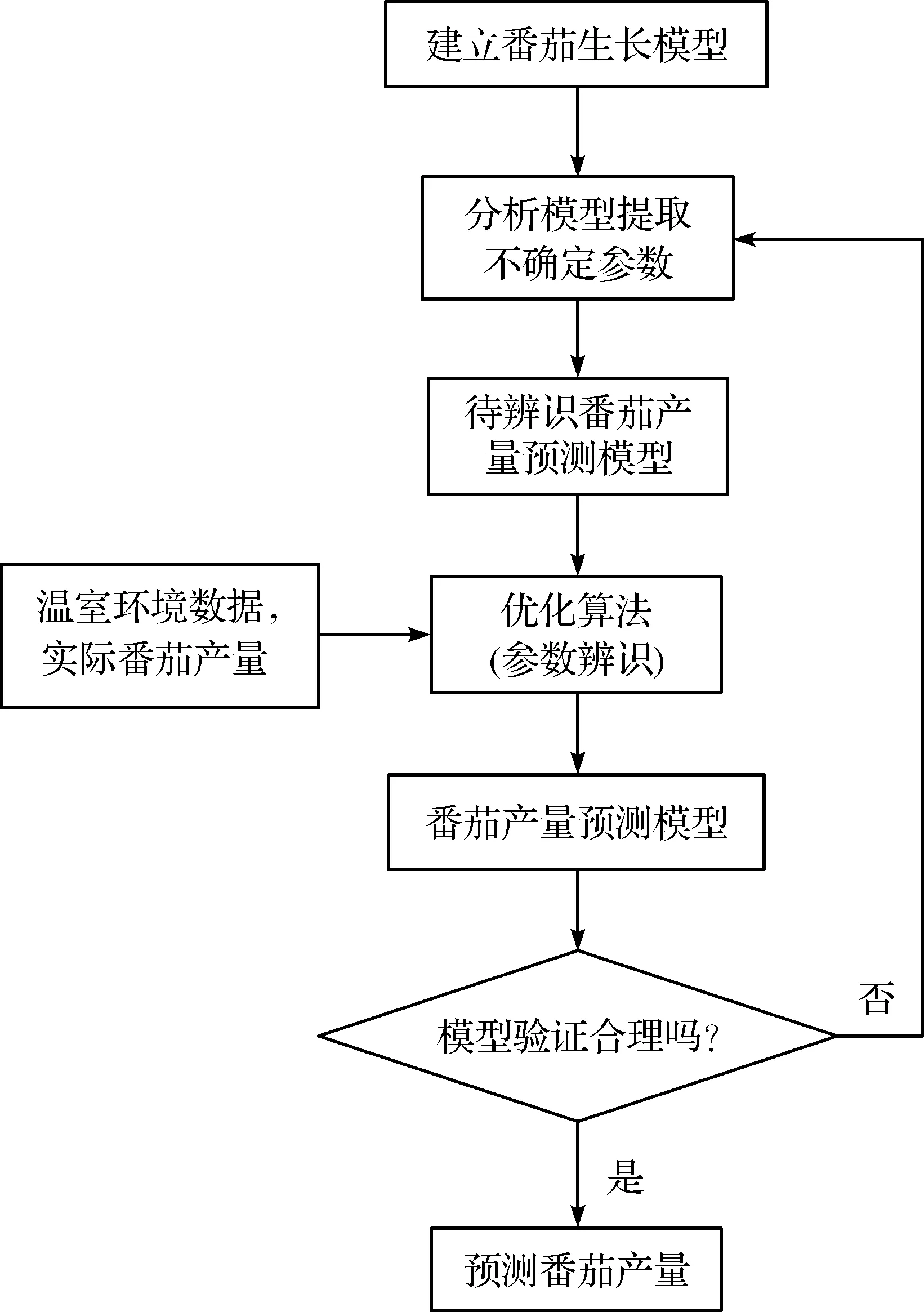
图1 番茄产量预测模型流程图Fig.1 Tomato yield forecasting model flow chart

2 番茄生长模型

在简化TOMGRO模型中，主要用果实干物质总量WF和成熟果实干物质总量WM两个变量来描述果实生长状态。地表干物质总量W、植株茎节数N和叶面积指数LAI被用来描述茎、叶等营养性器官的生长状态。简化TOMGRO模型通过植株茎节发育率、光合作用速率和呼吸速率计算植株地表干物质日生长率和不同器官的干物质分配比例，并引入新的函数用于模拟计算叶面积增长、生长性器官、果实和成熟的干物质分配比例。

温室无限生长型番茄生长发育过程在简化TOMGRO模型中分为生长期、结果期和成熟期。当植株上的茎节数达到NFF时，果实进入结果期。之后当茎节数增长KF时，认为果实进入成熟期。植株茎节发育率dN/dt忽略了CO2浓度对植株茎节发育的影响，具体模型描述为

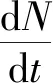
(1)

式中：Nmax为最大茎节生长率，在最适宜温度下一般为每天0.5 节；FN(T)为非最适宜温度下茎节发育率的下降趋势函数；T为室内温度，℃；Th为当天第h个小时的室内平均温度，℃。

番茄生长时的叶面积指数随时间的变化率可以表示为

(2)

式中：ρ为植株密度，株/m2；δ为相对于茎节的叶面积最大增长量，m2/茎节；β为茎节数在式中的相关系数；Nb为相关茎节数。

果实在一个特定的时间或者主茎节数达到NFF时开始发育，NFF指第一个果实直径超过10 mm时植株的主茎节数，WF在模型中可以用来表示果实开始发育后植株地上部分向果实输送的生物量。在求WF之前，首先要计算植株地上部分生物量增长率GRnet，即

GRnet=E·(A-Rm)·[1-fR(N)]

(3)

式中：A是日光合作用总量，以CH2O计，g/(m2·d)；Rm是日呼吸作用总量，以CH2O计，g/(m2·d)；函数fR(N)为每日地表生物量分配至根的部分；E为光合同化速率至干物质积累速率的转换系数。

从茎节数达到NFF后每天的果实干物质增长量dWF/dt可以表示为

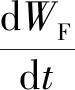
(4)

式中：函数fF(Td)表示正常的日平均温度Td对地上干物质总增长量分配至果实比例的影响函数；函数g(Tdaytime)表示白天平均温度超过26 ℃的高温环境对果实生长的影响，与Tdaytime有关；αF表示地表总生物量分配至果实的最大比例；θ表示营养性器官与果实生长率的转换系数。

叶面积指数达到最大值LAImax后，植物叶片会衰老或者被剪除，所以在计算地表总生物量时应该去除被剪除或者衰老的那一部分，地表植株干物质增长率的公式可表示为

(5)

式中P1表示叶面积指数LAI达到LAImax后因为日常的剪除叶面或植株衰老而产生的叶片干重损失率，g/茎节。先假设P1在LAI未达到最大时为0，在LAI达到最大后P1恒等于2 g/茎节。

高温条件下果实的生长率会下降，但植株内有较多碳水化合物未转化。假设营养性器官的最大生长率Vmax和最大地表总干物质增长率(dW/dt)max，用来限制果实的生长，公式为

(6)

移栽后，番茄在某天的植株地表干物质生长率dW/dt取上述两式计算结果的较小值。

简化模型中采用从第一颗果实出现到其成熟这段时间内的植株茎节差KF表示发育期时间延迟，为了描述第一个果实成熟后的所有果实发育情况，引入函数DF(Td)来表示所有果实成熟前的平均发育率，即

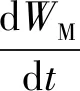
(7)

式中DF(Td)是日平均气温在第一颗果实成熟后对后续果实的发育影响函数。

结合以上公式，可得到温室番茄产量WM与时间t之间的关系为

WM(t)=f(t,P(t))

(8)

式中P(t)是简化TOMGRO模型中的环境变量，t是时间。

在种植地区、温室小气候条件、番茄品种发生改变时，简化TOMGRO模型中需要重新估计的参数包括用于描述成熟果实WM的两个参数：第一颗果实出现到成熟植株上增长的茎节数KF和成熟果实最大发育率DF max，以及用于描述番茄果实总干重W的4 个参数：地表总生物量分配至果实的最大比例αF、营养性器官与果实生长率的转换系数θ、出现第一颗果实时植株上的茎节数NFF和果实发生败育现象的白天气温临界值TCRIT。

3 改进型PSO-SA算法

粒子群算法[18]是一种通过研究鸟类和鱼类群体性觅食行为并结合演化计算理论提出的具有群体智能的全局优化算法。PSO算子在上一代粒子的基础上，更新速度和位置信息，得到新种群。其下一代的粒子的位置和速度信息向量分别为

Vi(t+1)=wi(t)Vi(t)+c1(t)r1(gi best-
xi(t))+c2(t)r2(Pbest-xi(t))

(9)

x(t+1)=x(t)+V(t+1)

(10)

式中：Vi(t)表示第i个粒子在第t次进化中的速度；r1和r2是(0, 1)之间随机数；gi best表示第i个粒子经过第t次进化之后产生的局部最优解；Pbest表示全局最优解；x(t)表示第i个粒子在经历第t次进化时所在的位置；w(t)表示第t次进化中的惯性权重；c1(t)和c2(t)分别表示第t次进化中的学习因子以及社会因子。惯性权重、学习因子和社会因子在种群进化过程中会不断变化以适应种群的变化。

SA算法思想最早是由Steinbrunn等[19]于1953年提出，称为Metropolis准则。SA算法是一种随机寻优算法，基于蒙特卡洛迭代求解策略，其基本根据为对物理中固体物质退火过程的模拟，以某个特定的概率接受优化问题的求解结果。SA算法结合概率突跳特性，在限制区域空间内采用随机搜寻的方法得到目标函数的全局最优解。由于一般需要解决的优化问题与固体退火过程有很大的相似性，使得SA算法成为一种通用优化算法，并得到广泛应用。

PSO算法公式简单和收敛快速，但是容易过早成熟而陷入局部收敛。而SA算法虽然全局寻优能力不强，但是能够在求解陷入局部收敛时概率性地跳出局部收敛，从而保证可以求得全局最优解。综合考虑上述两种算法的优缺点，笔者提出了改进型退火粒子群优化算法(IPSO-SA)。

为了加快IPSO-SA算法中PSO部分的搜索速度，加入了自适应算子操作，其目的是提高收敛速度和收敛精度，减少陷入局部较优的可能，包括自适应权重系数、社会因子和学习因子组成。权重系数ω、社会因子c1和学习因子c2分别为

(11)

(12)

(13)

式中：ωmax，ωmin分别为最大、最小惯性权重；(为加速因子；gi best表示第i个粒子在第t次进化后的局部最优解；Pbest表示全局最优解，c1 max，c1 min分别为最大、最小学习因子；c2 min是最小社会因子。

IPSO-SA算法的流程图如图2所示，具体过程为

1) 参数首次初始化：辨识粒子总数pop_size，模型中待辨识参数的个数以及其取值范围，PSO中的学习因子c1和c2的初始值，粒子最大速度向量以及最小速度向量，IPSO-SA迭代的总次数max_p，内嵌的种群代数max_s，降温系数以及初始温度T。

2) 对粒子种群进行初始化，单独一个种群中有pop_size 个粒子，每个种群都有一组辨识参数。确定适应性函数。比较适应度向量，可以挑选出全局最优粒子、全局最优适应度值、局部最优粒子种群和局部最优适应度向量。

3) 进行PSO计算。通过更新权重因子、速度因子和社会因子，接着更新粒子的速度和位置向量，得到新的种群。

4) 将更新后的粒子重新代入模型中，得到新一轮的值，之后依据适应性函数计算得到种群新的适应度向量。

5) 进入SA操作。将新种群通过SA规则替换旧种群。

6) 重选全局最优粒子，全局最优适应性值，局部最优粒子种群、局部最优适应度值。

7) 将当代粒子群作为下一代的初始种群。更新温度T、惯性权重、速度因子和社会因子后，算法跳至步骤3) 继续迭代，直到gen_max达到预设值。

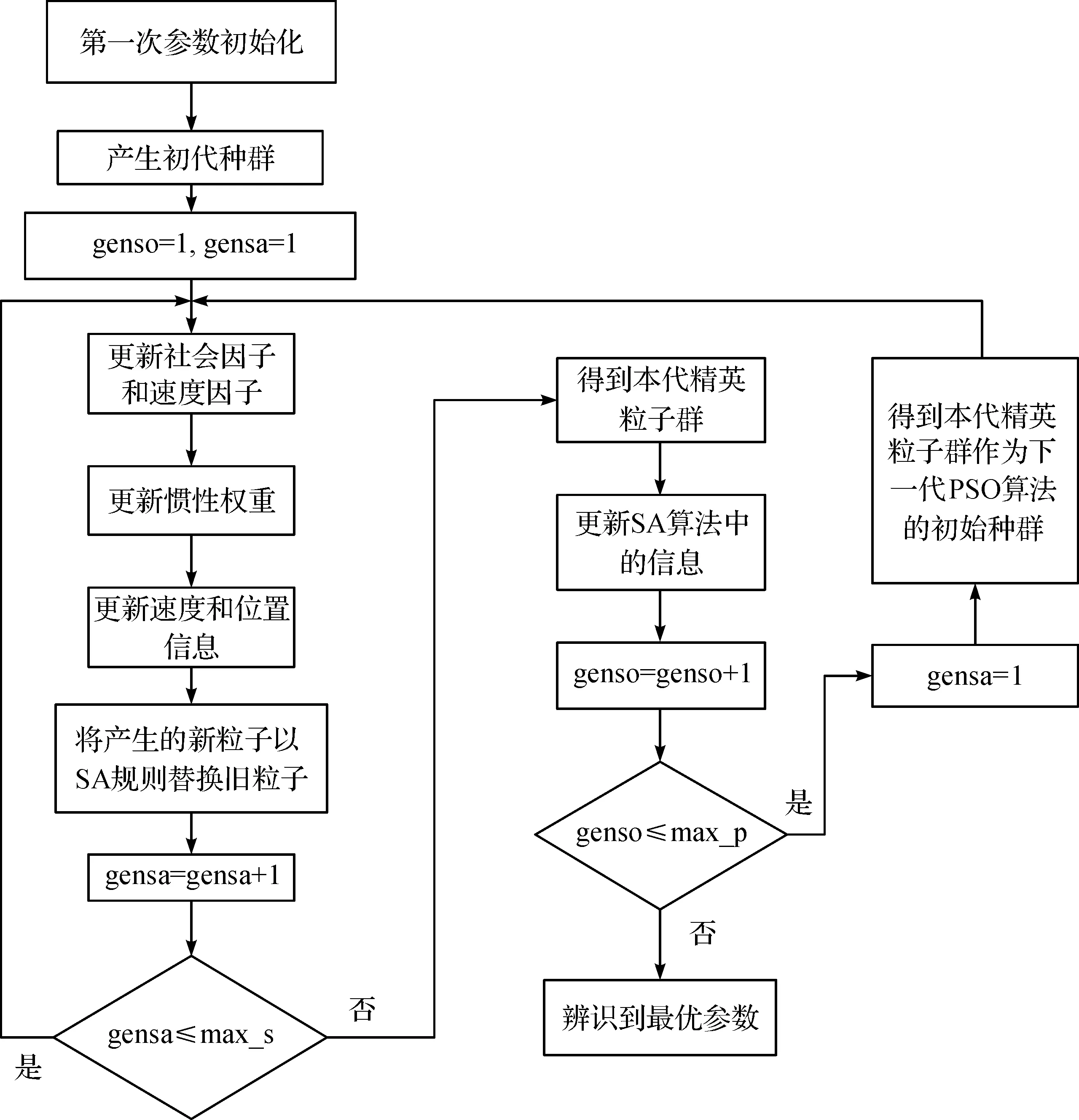
图2 IPSO-SA算法的程序流程图Fig.2 IPSO-SA algorithm program flow chart

4 结果与分析

4.1 参数辨识

分别在Matlab中编写PSO，SA，IPSO-SA以及简化TOMGRO模型的M文件代码。采用2015年9月30日—2016年5月12日之间的室内温度、CO2浓度、光照强度和番茄生长数据进行参数辨识。考虑到不同算法的收敛速度，将算法总代数初始化为300，保证所有算法都能完成求解。优化算法在求解过程中调用简化TOMGRO模型计算适应度函数值，辨识出模型中的不确定参数。参数辨识的结果如表2所示。

表2 参数辨识结果Table 2 Parameter identification result

根据IPSO-SA，PSO，SA每一代的均方根误差，可分别得到3 种算法的收敛情况，如图3所示。该图显示SA在第32 代时陷入局部收敛，直到第240 代时又跳出了局部收敛，表明SA具有良好的全局求解能力。PSO运行至第20 代时就已完成收敛。而IPSO-SA在第3 代时达到收敛，此后分别在第65 代时跳出局部收敛。表明IPSO-SA不仅继承了PSO在前期快速收敛的特性，而且融合了SA全局搜索的优点，具备了较强的跳出局部收敛的能力。

根据优化算法辨识获得的参数(表2)，结合温室番茄产量预测模型获得3 种优化算法模拟番茄的产量，如图4所示。在移植后第77 d左右和种植周期结束时，IPSO-SA算法跟随实际番茄产量的能力要高于其他两种算法，可知IPSO-SA算法的鲁棒性更强，对于果实成熟的响应更快。PSO和SA最终收敛时的均方根误差分别比IPSO-SA要大90.8%和55.5%，可见IPSO-SA模拟和实际产量的偏差要小于其他两种算法。

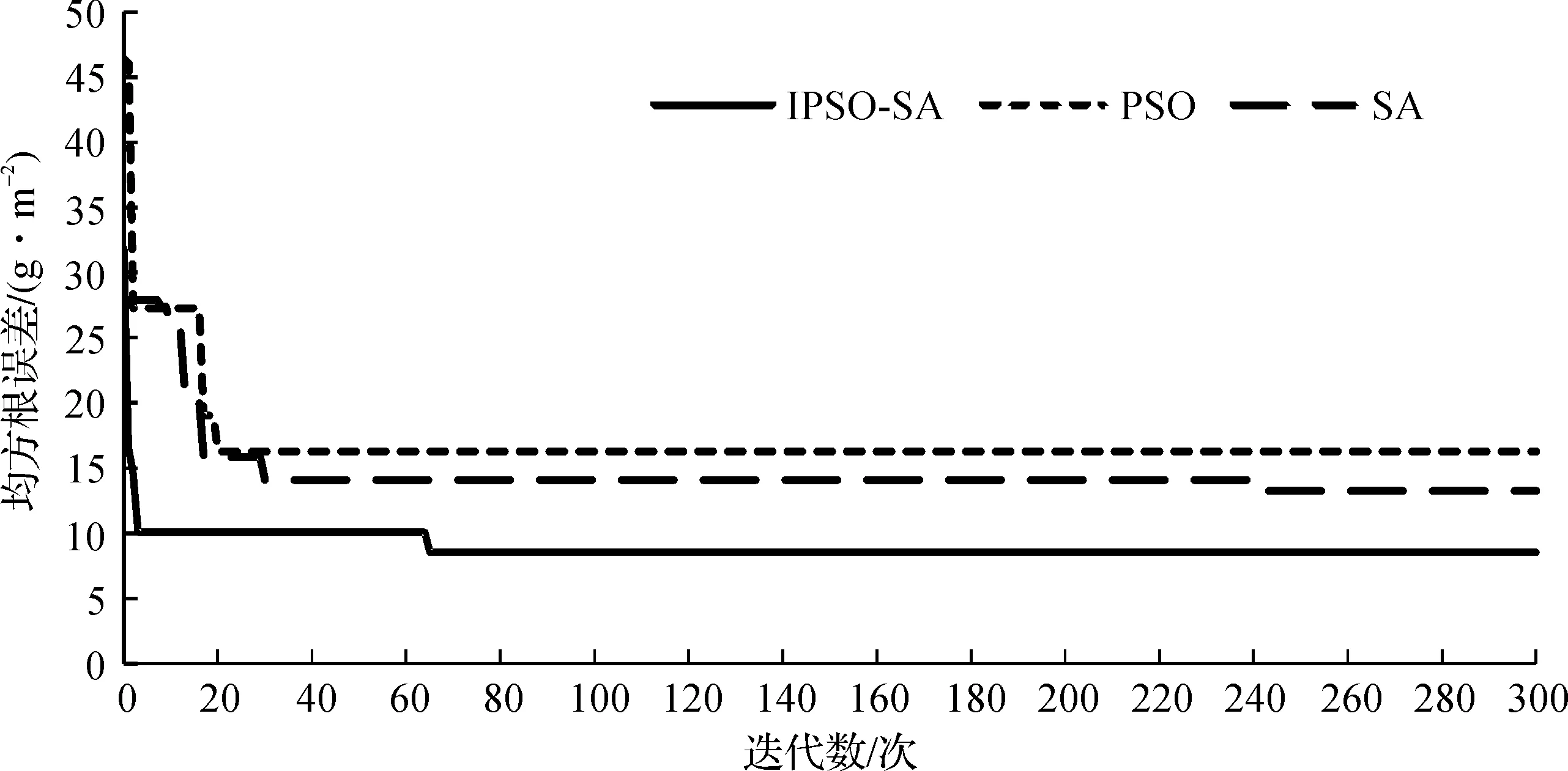
图3 3 种算法收敛情况Fig.3 Three kinds of algorithm convergence

图4 辨识过程中3 种优化算法产量预测值和实测值Fig.4 Experimental and forecasted yield with three algorithms in identification process

4.2 产量模型验证

采用2016年9月30日—2017年5月12日期间的温室环境数据和番茄生长数据对温室番茄产量预测模型进行验证。为排除偶然误差，先利用2015年9月30日—2017年5月12日期间的相应数据进行10 次参数辨识，IPSO-SA，PSO，SA等3 种算法分别运行10 次得到10 组参数，即10 个模型。然后利用得到的模型和2016年9月30日—2017年5月12日期间的相应数据对该生长周期的番茄产量进行预测，对预测值取平均，结果如图5所示。

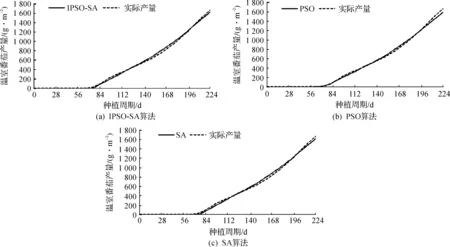
图5 验证过程中3 种优化算法产量预测值和实测值Fig.5 Experimental and forecasted yield with three algorithms in forecasting process

虽然3 种算法校准后的模型均能较好地预测番茄产量，但是根据196～224 d内的产量曲线可知：IPSO-SA预测的产量更接近实际值。IPSO-SA预测的总产量与实际总产量的相对误差为2.2%，比PSO和SA分别要小2.1%和0.7%，PSO和SA均方根误差的平均值分别比IPSO-SA高66.1%和17.7%，表明IPSO-SA的参数辨识能力要优于PSO和SA，预测的总产量精度高达97.8%。

5 结 论

笔者将PSO算法与SA算法结合并引入PSO算法的自适应算子操作加速算法的收敛，辨识得到产量模型能很好地预测温室番茄产量。通过实际模拟分析，将IPSO-SA算法用于简化TOMGRO模型参数辨识时，搜索最优解的收敛速度和收敛精度均有较大提升。校准后的简化TOMGRO模型可预测温室番茄不同温度条件下一个生产周期的总产量，对温室番茄栽培具有一定指导意义。由于温室环境以及植物生长过程的复杂性，为更精确地预测温室番茄产量，需考虑昼夜温度分开设定对番茄产量的影响，并结合室外气候变化进行下一步的研究。