基于季节因素修正的GM(1,1)模型在高速公路车流量预测中的应用
2019-09-21孙世忠
孙世忠
(河北省高速公路衡大管理处,河北 衡水 053000)
1 高速公路车流量预测的必要性
高速公路车流量,就是单位时间内某条高速公路上所通过的车辆数。在工程建设和行业管理实践中对高速公路车流量一直缺乏行之有效的预测方法,加上一些人为干扰,造成许多项目前期车流量预测数据与项目建成后实际车流量相差甚远,造成了严重的决策偏差和投资浪费,因此有必要结合高速公路车流量特点,探索合理可靠的高速公路车流量预测方法,为高速公路前期规划决策、运营期经营效益评估,以及建设项目后期评价提供可靠的数据支持。
2 车流量预测方法概述
对于某条段高速公路或某区域高速路网来说,车流量大小主要受收费标准高低的影响;随着高速路网的不断完善和加密,车流量大小与周边相邻路段或路网畅通状况有关,因此高速公路车流量临时不确定性因素较多,而且受季节和天气因素影响波动变化较大。
针对这种变化特点,以河北省衡大高速公路近4 a的季度车流量数据为例,分别基于常规GM(1,1)灰色模型和季节因素修正GM(1,1)模型两种方法进行计算对比。
2.1 常规GM(1,1)灰色模型法
2.1.1 基本原理
按季度统计的高速公路车流量数据可以视为一个时间序列,从统计学角度看,时间序列分析是基于趋势预测原理进行的,如果时间序列变化趋势不明显,则很难建立拟合度比较高的预测模型;同时,时间序列分析是基于时间序列按照既定趋势变化的假设条件为前提,没有考虑不确定因素对未来变化产生的影响。而当一个时间序列没有表现出明显趋势的态势时,使用累加的方法可以将无序离散的原始序列转化为一个增长趋势较为明显的时间序列,按该序列的增长趋势可以建立指数型预测模型,并考虑不确定性的影响进行预测,最后采取累减的方法恢复原来的时间序列,从而得到预测结构,这就是GM(1,1)灰色预测的基本原理[1,2]。具有要求原始数据数量少、精度相对较高的特点,适合小样本、贫信息不确定性系统的分析。
2.1.2 模型建立的步骤和方法
GM(1,1)灰色预测模型反映了一个变量对时间的一阶微分函数,其相应的微分方程为

(1)
式中:x(1)为经过一次累加生成的数列;t为时间;a,u为待估参数,分别称为发展灰数和内生控制灰数。


(3)对x(1)采用最小二乘法求参数a,u。
其中

(3)
yn=[x(0)(2),x(0)(3),…,x(0)(n)]T
(4)

(5)
2.2 季节因素修正GM(1,1)模型预测方法
2.2.1 方法基本思路
GM(1,1)模型预测虽然具有要求样本数据少的优势,但作为一种预测方法,由于其基本原理是用指数曲线拟合原始数列,因此对于序列数据出现异常的情况很难处理,特别是对高速公路车流量这类存在季节波动变化的时间序列,其拟合效果有待提高。有必要引入季节因素进行修正,使其既能反映时间序列的趋势变化,又考虑季节波动影响[2,3]。
2.2.2 基本步骤
(1)基于GM(1,1)模型预测方法得出各季度预测值,作为趋势值。
(2)将各季度原始数据除以趋势值,得出修匀比率,使增长趋势的影响得以消除,以表明各季度的季节变动程度。
(3)将各年同季度的修匀比率加以平均,得到各年同季度的平均修匀比率。
(4)将各年同季度的平均修匀比率加以平均,得到季度总平均修匀比率。
(5)用季度总平均修匀比率对季度平均修匀比率进行调整来确定季节比率。
2.3 计算预测值并进行误差检验
根据季节比率,测算出各季度预测值,并根据实际值和预测值计算标准误差,检查预测值是否在标准误差范围之内。
3 高速公路车流量实例预测及分析
河北省衡大高速公路近5 a来车流量情况如表1所示。
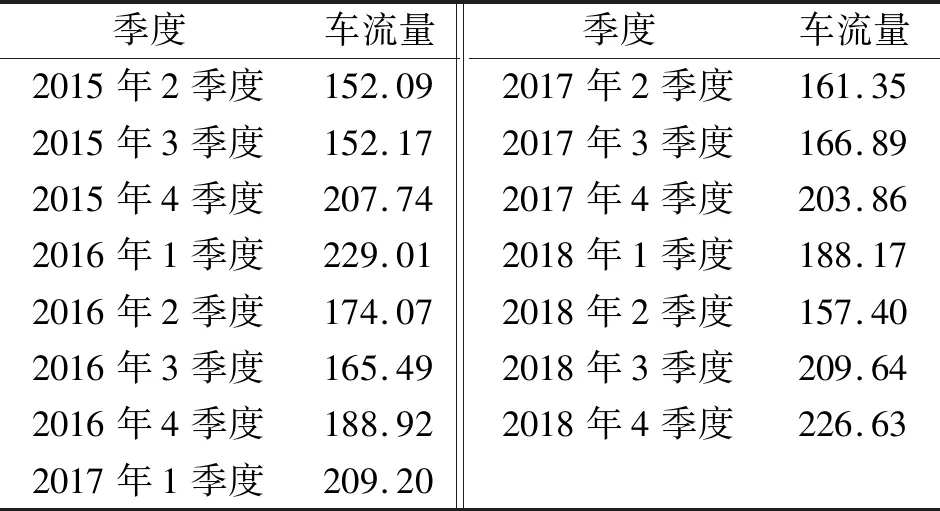
表1 季度车流量数据 万辆
3.1 基于常规GM(1,1)灰色模型预测
3.1.1 原始数列数据处理
利用公式(2)原始数列生成累加数列,并对其进行数列准光滑性检验和准指数检验,判断是否可以对X(1)应用GM(1,1)模型,计算结果如表2所示。
当k>3时,ρ(k)<0.5,满足准光滑条件;同时σ(1)(k)∈[1,1.5],满足准指数条件,因此,X(1)累加数列适用GM(1,1)模型。
3.1.2 确定GM(1,1)模型


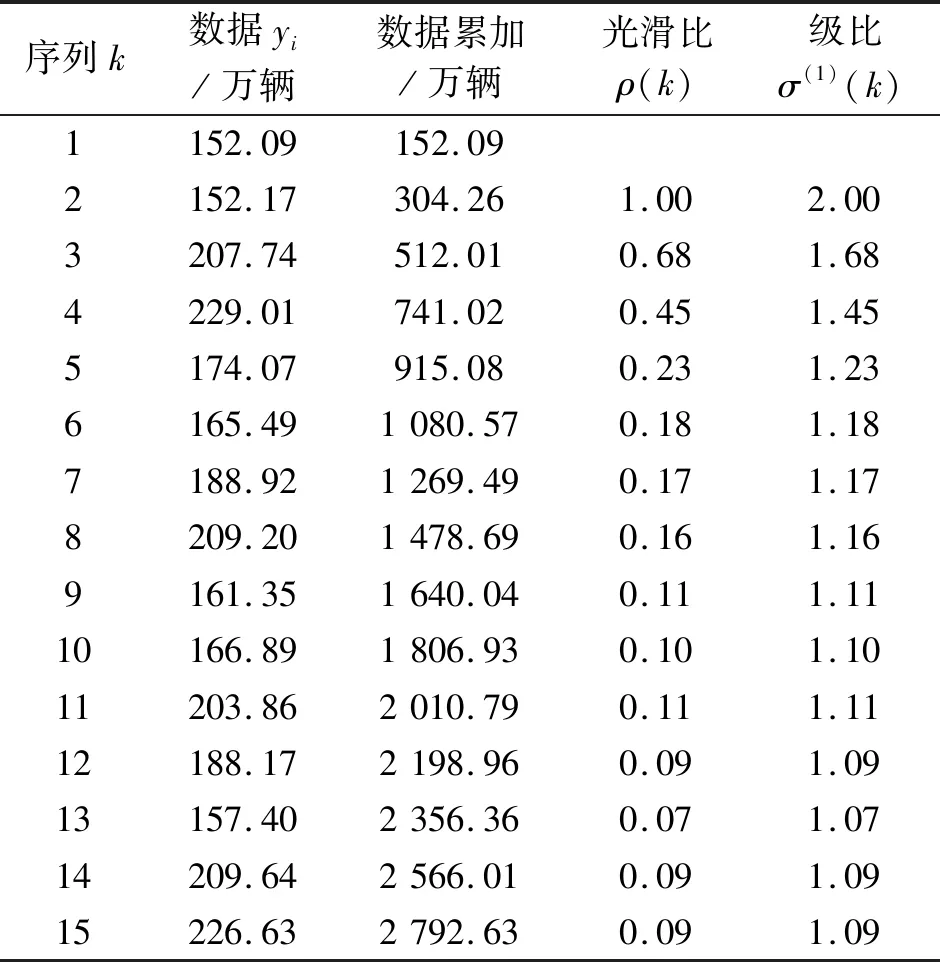
表2 准光滑性检验和准指数检验
3.1.3 推算季度趋势值
根据公式(5)推算各季度趋势值,结果如下:
当k=0时,x^(1)(1)=28 925.376 316e(0.000 000)-28 773.283 416=152.092 900
…
当k=14时,x^(1)(15)=28 925.376 316e(0.087 357)-28 773.283 416=2 792.575 990
因此:X^(1)=(152.092 900 ,333.145 025 ,515.330 407,698.656 138,883.129 358,1 068.757 247,1 255.547 034,1 443.505 991,1 632.641 436,1 822.960 734,2 014.471 294,2 207.180 574,2 401.096 075,2 596.225 348,2 792.575 990)
X^(0) = (152.092 900,181.052 125,182.185 382,183.325 732,184.473 219,185.627 889,186.789 787,187.958 957,189.135 445,190.319 298,191.510 560,192.709 279,193.915 501,195.129 273,196.350 643)
以此类推,可推算2019年各季度趋势值:
k=15时,x^(0)(15)=2 990.155 647-2 792.575 990=197.579 657 ;k=16时,x^(0)(16)=3 188.972 011-2 990.155 647=198.816 364 ;k=17时,x^(0)(17)=3 389.032 823-3 188.972 011=200.060 812;k=18时,x^(0)(18)=3 590.345 872-3 389.032 823=201.313 049。即2019各季度趋势值分别为197.58万辆、198.82万辆、200.06万辆、201.31万辆。
3.1.4 趋势值误差检验
根据实际值和趋势值计算残差及其标准差,检查预测值是否在允许误差范围之内,结果见表3。

表3 GM(1,1)模型误差计算
按95%的概率计算,只容许最多有一点(15×0.05≈1)可以超出控制范围,表3中的所有残差均未超出控制范围。
3.2 基于季节因素修正模型
3.2.1 常规GM(1,1)模型数据处理
对原始数列按照常规GM(1,1)模型进行处理,得到原始数列的趋势值及2019各季度趋势值。
3.2.2 计算趋势比率和季节比率
(1)将各季度原始数据除以趋势值,得出趋势比率,使增长趋势的影响得以消除,以表明各季度的季节变动程度。趋势比率的计算式Ui=yi/yc,如2015年第3季度为152.17/181.05=84.05%,2016年第4季度为188.92/186.79=101.14%。以下各季度同此计算,于是得出表4。

表4 季节修正模型参数 %

根据该式,对趋势比率进一步计算,得到各季度平均趋势比率:第1季度,111.29% ;第2季度,90.21%;第3季度,92.08%;第4季度,109.26%。

(4)用季度总平均趋势比率对各季度平均趋势比率进行调整,确定季节比率:第1季度,110.50%;第2季度,89.57%;第3季度,91.43%;第4季度,108.49%。季节比率具体计算详见表4。
3.2.3 计算预测值并进行误差检验
将季节比率和各季度趋势值相乘,测算出各季度预测值,并根据实际值和预测值计算残差及其标准差,检查预测值是否在允许误差范围之内,结果见表5。

表5 GM(1,1)季节修正模型误差计算
按95%的概率计算,只容许最多有一点(15×0.05≈1)可以超出控制范围,表6中的所有残差均未超出控制范围。
以此类推同样可得出2019各季度通行量预测值分别为197.58万辆×110.50%=218.33万辆、198.82万辆×89.57%=178.09万辆、200.06万辆×91.43%=182.92万辆、202.57万辆×108.49%=219.77万辆。
3.3 两种方法结果对比
将常规GM(1,1)模型法和GM(1,1)季节修正模型法的计算结果进行比较,可以看出:使用这两种方法算得的预测值的误差都在允许范围之内,但前者标准误差(27.797)和平均相对误差(11.7%),要远大于GM(1,1)季节修正模型法所得的标准误差(18.312)和平均相对误差(7.1%),因此使用GM(1,1)季节修正模型法误差更小,预测出来的值更为接近真实数据。
4 结束语
本文对常规的GM(1,1)模型进行季节比率修正,使其既能够反映时间序列的趋势变化,又能够反映季节波动的影响,可以有效减小误差。当然,从长期预测的角度看,不仅要考虑季节因素,还要综合考虑周边路网变动、交通管制等内外因素的影响,在实际应用中,可探讨适当加入外部因素影响进一步修正预测值,不断验证方法的可靠性、提高预测精度。
