基于KM-FNN的无线传感器网络缺失数据重建算法*

武加文,李光辉*

(1.江南大学物联网工程学院,江苏 无锡 214122;2.物联网技术应用教育部工程技术研究中心,江苏 无锡 214122)

通过将客观物理世界与信息世界紧密的相联,无线传感器网络(Wireless Sensor Network,WSN)极大地提高了人们对真实世界的认识能力[1]。然而,在环境监测领域,WSN通常被部署于无人监管、气候复杂的野外环境,一方面,受到低成本传感器节点资源的限制,例如电池功率、计算存储能力以及通信带宽,这使得节点产生错误数据的概率很大。另一方面,数量庞大地传感器节点通常随机部署在环境恶劣的外界环境,伴随着极端气候的影响,如狂风,暴雨,冰雹等,一些节点发生故障也是不可避免的。因此,在长期使用过程中,WSN经常发生数据缺失现象[2]。若不精确重建这些缺失数据,可能会影响整个网络数据的可靠性以及监测数据流的完整性。例如,当监测环境发生事件(如森林火灾、水质或空气污染等)时,不可靠且不完整的数据可能导致系统无法实时检测到类似的自然灾害,从而造成重大损失。因此,快速准确地重建缺失数据具有重要意义。

关于WSN数据重建方法,国内外学术界已有诸多成果[3]。现有的WSN数据重建方法主要是利用感知数据的先验信息,这在一定程度上可以恢复丢失的数据。利用节点间的空间相关性,文献[4]提出了一种克里金插值方法,通过考虑缺失数据的空间位置及分布信息,利用不同系数加权平均得到待插点的估计值。文献[5]在文献[4]的基础上,加入贪婪算法用以去除误差评估最优的传感器节点,从而有效地减少了部署的传感器节点,降低了时间复杂度。文献[6]将节点的感知数据映射至图表,并引入互连矩阵和系统图等概念,构建了一个传感器网络实时预测的模型用以重建缺失值。文献[7]提出了一种基于二次规划的感知数据恢复的方法。该方法将重建过程转换为有界约束二次规划问题,并通过求解Armijo规则的二次规划问题,从而有效地恢复了数据。文献[8]提出了一种数据挖掘的方法(CARM)重建缺失数据。该方法通过关联规则挖掘感知数据得到节点之间的频繁模式,以恢复缺失值。

基于传感器节点的时间相关性与空间相关性,文献[9]提出了基于时间相关性的数据重建算法LIN和基于空间相关性的数据重建算法MR。LIN考虑到数据的时间相关性,连续时刻的节点数据是近似的。如果当前时刻数据缺失,可以利用前一时刻和后一时刻的数据来估计当前时刻的数据。MR主要是利用节点部署的空间相关性,即相邻节点的感知数据具有相似性,因此,基于邻居节点的数据重建目标节点的缺失数据。目前,已有多种机器学习方法被用来解决数据缺失问题,如决策树、贝叶斯法、期望值最大化、回归法等。其中,大多数方法是利用已有的正常数据作为训练样本,从而建立预测模型,以估计缺失数据[10]。然而,一旦预测值不精确,将导致数据重建的精度受到累积误差的限制。

针对上述问题,本文提出了一种基于自适应的K-均值算法与模糊神经网络相结合的WSN缺失数据重建算法(KM-FNN)。KM-FNN应用于分簇式WSN的簇头节点上,使用模糊神经网络模型重建缺失数据并引入自适应机制用来及时更新训练模型。KM-FNN可以实时向基站汇报存在数据缺失的节点序号以及重建后的完整数据流。实验结果表明,相较以往同类算法,KM-FNN具有更精准的缺失数据重建精度。

1 基本概念

1.1 分簇式无线传感器网络模型结构

本文基于分簇式WSN进行仿真实验,将邻近区域内的节点分为一个簇,每个簇包含簇头节点和一定数量的成员节点。通常,簇内成员节点只负责采集感知数据,并将数据传送至簇头节点,由簇头节点负责分析与处理这些数据[11],其结构如图1所示。

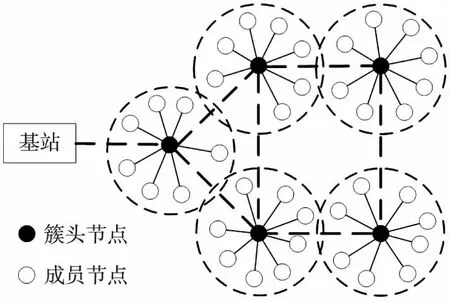
图1 分簇式WSN结构

1.2 模糊神经网络

模糊神经网络FNN(Fuzzy Neural Network)是一种用于预测的神经网络系统。其中,隶属度与隶属度函数是FNN中最基本的概念[12]。隶属度是指某一元素u隶属于某一模糊子集A的程度,见式(1)。隶属度函数是用来计算元素隶属度的函数,一般为正态函数。

(1)

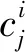
FNN的自适应力极强,可以自动更新模糊子集的隶属函数。基于规则,其推理规则如下[13]:

(2)

1.3 性能评价指标

本文选用均方误差和决定系数作为WSN缺失数据重建算法的性能评价指标。其中均方误差MSE(Mean-Square Error)表示预测值与被预测值之间的差异程度,见式(3)。一般情况下,MSE越小,表明预测值与被预测值之间差异程度越小。MSE越大,表明预测值与被预测值之间差异程度越大。而决定系数(coefficient of determination)R2表示所建立的预测模型对被预测值的拟合程度。R2的取值范围一般在区间[0,1]。若该值越接近1,表明模型的拟合程度越高,即性能越好。相反,越接近0,表明模型的性能越差。

(3)

(4)

式中:n表示样本数目,与分别为第i个样本的被预测值与预测值。

2 KM-FNN数据重建算法

2.1 算法概述

通常情况下,在分簇式WSN中,传输至簇头节点的数据中会存在一定量的数据缺失。若能在簇头节点将数据发送至基站前重建缺失数据,这样会大大节省了后续的工作。同时考虑到真实的WSN受外界自然环境的影响较大,导致感知数据分布的情况随着时间的推移产生了复杂的变化。因此,本文提出了基于自适应的WSN缺失数据重建算法KM-FNN。KM-FNN首先使用传输至簇头节点的初始感知数据建模用以预测缺失值,然后引入自适应机制用来在线更新模型以适应感知数据的变化。自适应机制的实现主要依赖于滑动窗口的引入以及模型的在线更新准则KM算法。KM-FNN运行在簇头节点上,能够实时自适应地重建节点的数据缺失,并向基站汇报存在缺失值的成员节点编号以及重建后的完整数据序列。

2.2 FNN的建模过程

模糊神经网络的优势是具有较强的自适应能力和并行分布式的数据处理能力。因此,采用模糊神经网络对节点间的时空相关性建模。将WSN部署初期(假设此时无缺失数据)的目标节点i和其邻居节点的感知数据作为训练数据集,训练数据集可以被划分为Train={TX;TY}。TX表示训练数据输入,TX={xj,t:j=1,2,…,m;t=1,2,…,w},TY表示训练数据输出,TY={xj,t:t=1,2,…,w}。其中,j表示节点序号,t表示时序。m表示节点i的邻居节点的个数,w表示节点i的感知数据的个数。基于FNN算法的WSN数据重建的算法流程参见图2。

图2 FNN建模流程

如图2所示,网络的输入,输出节点数由TX与TY的维度而确定,并随机初始化模糊隶属度的函数中心c,宽度b等参数。综上,FNN建模的具体方法如下:首先,根据数据集的划分情况确定网络结构,初始化网络参数,并初始化隶属函数和模糊规则。其次,使用训练集训练得到网络模型,并进一步更正隶属函数和模糊规则。最后,在训练模型中输入测试集并输出预测值,完成缺失数据的重建。

2.3 自适应机制的实现

在环境监测领域,真实的WSN易受外界自然环境的影响导致感知数据的分布情况随着时间的推移产生了复杂的变化。如果一直采用固定的神经网络模型用于缺失数据的重建,则该算法的鲁棒性以及适用性会受到很大影响[14]。由于节点数据在传输过程是以数据流的方式传输,其传输方式是实时的,连续的。为了更好地模拟算法在WSN上的真实应用过程,引入了滑动窗口机制,针对节点的数据流选取了一个固定长度的窗口,用于观测节点最近一个时间段内采集的数据流的变化状况。

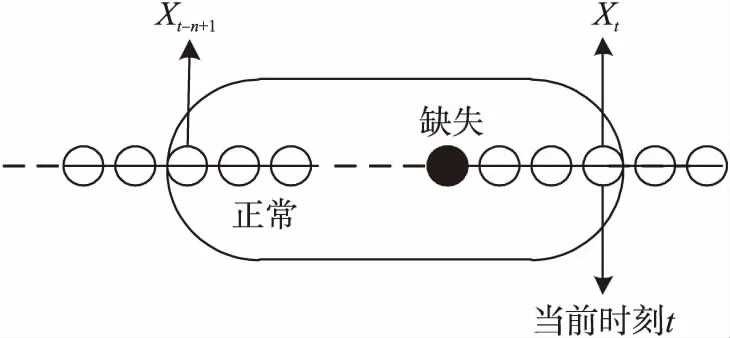
图3 数据流滑动窗口模型

图4表示在IBRL数据集中1号节点于2004年3月1日0:00～7:00和12:00～20:00的温度分布情况。IBRL数据集来自于2004年2月28日到2004年4月5日期间部署在Intel Berkeley实验室内的无线传感器网络,共包含54个节点。每个节点以31 s的采样周期采集四种属性数据,包括温度、湿度、光照及电压值。图4(a)表示0:00～7:00时间段内的温度随时间的变化情况,图4(b)表示12:00～20:00时间段内的温度随时间的变化情况,由图4可知,随着时间的流逝,数据的分布情况发生了较大的变化。因此,若采用固定不变的模型预测缺失数据会导致重建精度的累积下降。

图4 不同时间段的数据分布情况

KM-FNN使用K-均值算法(k-means)作为更新准则,其思想是把数据分配至距离其最近的类中心的归属类,类中心由属于该类的全部数据决定[15]。结合K-均值算法,提出的基于数据分布的自适应算法KM的伪代码见表1。其中,x表示待加入滑动窗口的数据,x之前的数据被划分为k类,每类中包含Mh个数据,其中心数据为AMh,其中h=1,2,…,k。

如表1所示,KM的实现过程如下。当新数据加入滑动窗口时,首先判断该数据是否缺失。若不缺失,则快速判断其所属的类别,并更新所属类别的中心数据,然后计算完整数据的MSE,该值为Eb。当该数据缺失时,使用当前的FNN模型预测该数据,并将预测值作为新数据加入滑动窗口中。重复上述操作,直到所有数据处理完毕。

综上所述,KM-FNN的实现步骤如下。首先在簇头节点中汇集初始阶段的N个成员节点的感知数据,并将各个节点数据均按照K-均值算法的思想,划分为k类,并分别计算每类中单个数据与中心数据的MSE,然后求k个MSE的平均值,得到总体MSE值Ea。对于待测试的成员节点i,设其邻居节点的个数为mi,然后根据节点i和其邻居节点的感知数据建立FNN模型,表示为FNNi。即初始阶段,簇头节点中建立N个网络模型。在下一时间段内,簇头节点收到节点i的测试数据x=x1,x2,…,xq。

表1 KM自适应算法

表2 KM-FNN数据重建算法

3 实验结果与分析

为了验证KM-FNN算法的算法性能,在MATLAB 2013b 的实验环境下针对不同的真实数据集下分别实现了提出的KM-FNN算法、LIN算法[9]、MR算法[9]和小波神经网络(wavelet neural network,WNN)算法[16],并比较了实验结果。

3.1 实验数据集

①IBRL数据集

选取了由IBRL部署中的两组节点的数据子集作为实验对象。第一组数据子集(IBRL_1)包含的节点ID分别是1,2,3,4,6,7,10,33。第二组数据子集(IBRL_2)包含的节点ID分别是17,18,19,20,21,22,23。两组数据集都对应于2004年2月28日至2004年3月7日九天内所收集的数据。

②LUCE数据集

LUCE数据集(洛桑城市冠层实验)来自于2006年7月以来部署在洛桑联邦理工学院内的无线传感器网络。该网络共包含97个节点,根据节点之间的时空相关性分为10组传感器节点集。在2006年10月1日到2007年5月9日期间,每个节点以31 s的采样周期采集六种属性数据,包括环境温度、地表温度、相对湿度、太阳辐射、土壤水分及风向。选取了LUCE数据集中的两组节点的数据子集作为实验对象,第一组数据子集(LUCE_1)包含的节点ID分别是10、14、15,17、18、19。第二组数据子集(LUCE_2)包含的节点ID分别是81、82、85、86、87、89。两组数据子集都对应于2007年1月1日至2007年1月30日三十天内所收集的数据。

③JNSN数据集

JNSN数据集来自于江南大学智能感知与无损检测实验室部署在校园内的无线传感器网络系统。该系统由30个普通传感器节点、汇聚节点、数据转发设备和服务器构成。节点的分布参见图5。

图5 传感器网络节点部署图

在2018年4月25日到2019年3月10日期间,每个传感器节点以10 min的采样周期采集三种属性数据,包括环境温度、相对湿度、光照强度。然后将感知数据通过汇聚节点汇总至无线自组网系统中,在终端服务器中调试算法以及分析数据。选取了JNSN数据集中的数据子集(JNSN_1)包含的节点ID分别是1、2、3、5、6、7,对应于2018年6月14日到2018年8月11日所收集的数据。

为了削减数据集,并保证训练集中不存在缺失数据,以模拟节点部署初期的感知数据。针对来自IBRL_1,IBRL_1,LUCE_1,LUCE_2和JNSN_1的数据分别以4.5 min间隔、5 min间隔、70 s间隔,35 s间隔和27 min间隔重新采样。采用温度作为评估数据。表3列出了所使用的所有数据集。

表3 实验所用数据集

在数据集中查找是否出现缺失值,经过统计发现,在测试集中出现了不同程度的数据缺失,其缺失位置用NAN代替。表4表示实验数据集中缺失数据的分布情况。

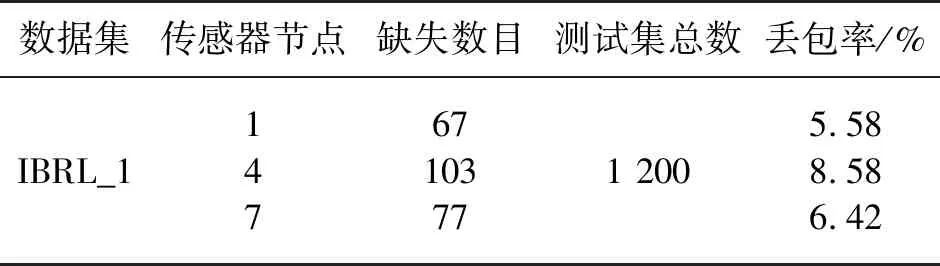
表4 数据集中缺失数据的分布情况(a)IBRL_1数据集

(b)IBRL_2数据集

(c)IUCE_1数据集

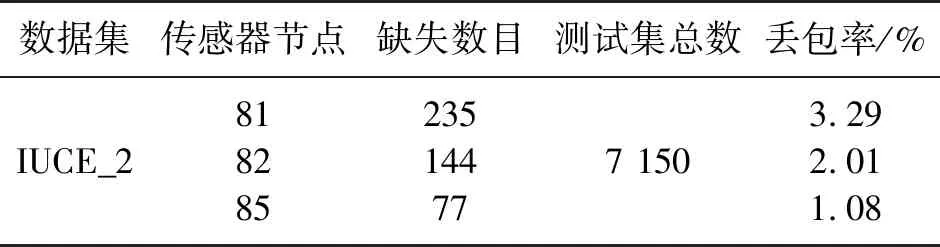
(d)IUCE_2数据集

(e)JNSN_1数据集

3.2 实验结果

由于节点数据随着时间的推移,其数据分布发生了较大的变化,KM算法将具有对应分布特征的节点数据分为k类,建立k个模型以满足当前节点的分布规律。图6(a)表示数据集I中1号节点于2004年3月1日内的完整数据。图6(b)数据集I中1号节点于2004年3月1日至2004年3月3日三天内的完整数据。其中,设k值为4。

图6中取k值为4。即数据根据其分布的特征规律划分为4部分,划分的边界值分别为:第一类边界[17.195 4,19.106 4],第二类边界[19.243 6,21.438 8],第三类边界[21.458 4,23.781 0],第四类边界[23.820 2,26.133 0]。首先计算四类样本的单个数据与类别中心数据的MSE值,然后计算四个类别的平均MSE,其大小为0.257 5。设k值为3并重复上述实验,其大小为2.013 3;设k值为2,其大小为3.829 5。通过比较可知,当k取值为4时,数据分布的平均MSE值最小,这表明当前数据的分布较均衡。若取k值为5以上时,算法的复杂度过大,不合适真实场景的应用。因此,为了更好地重建缺失数据,故所有实验均选择k为4。

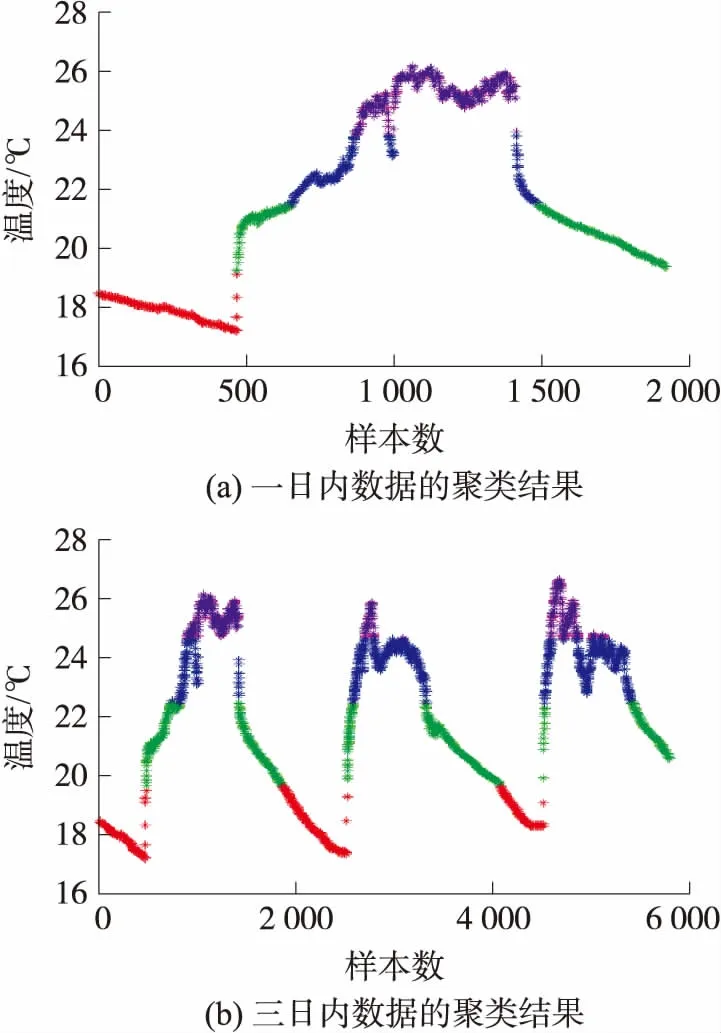
图6 数据集I下1号节点数据的聚类示例

分别选择IBRL_1下1号节点,IBRL_2下17号节点,IUCE_1下10号节点,IUCE_2下81号节点,JNSN_1下1号节点,JNSN_2下8号节点实施了3次对比实验,并选取平均值作为最终数据,表5给出了各算法关于5个数据集的实验结果。可以看出,CELM的平均均方误差比WNN、LIN、MR分别减少了0.842,0.994,0.381。CELM的平均决定系数比WNN、LIN、MR分别提高了6.65%,5.94%,2.82%。

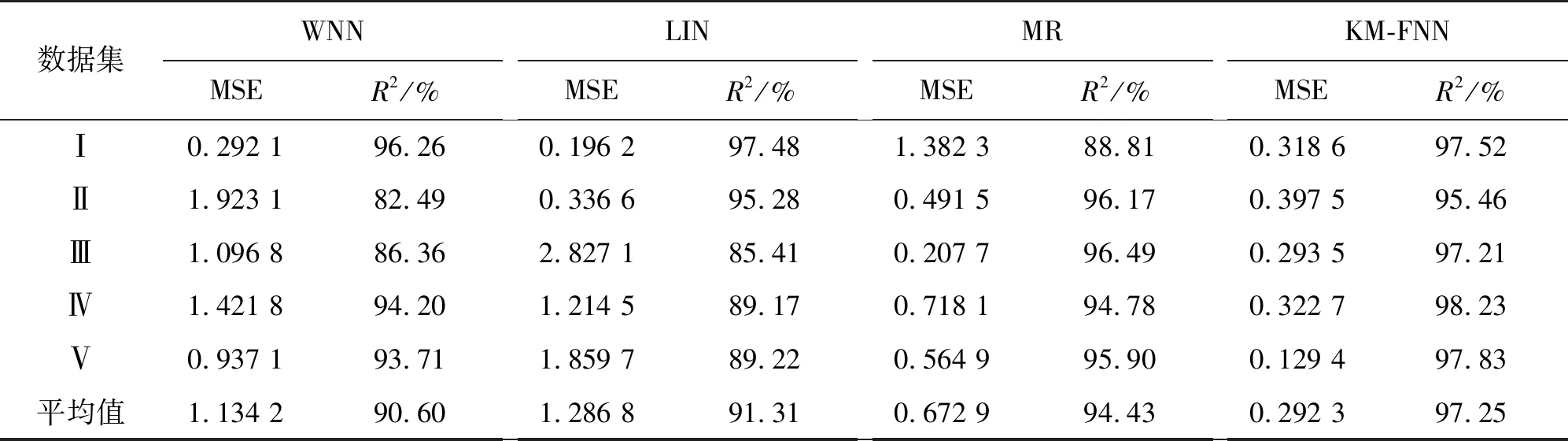
表5 四种算法的数据重建对比结果

为了验证不同数量的缺失数据对实验的影响,使用四种算法在数据集Ⅲ和Ⅴ下分别针对17号节点和7号节点的数据进行实验。其中,在两个节点数据的测试集随机位置中分别删去数量为10,20,30,40,50,60的数据。实验结果见图7。

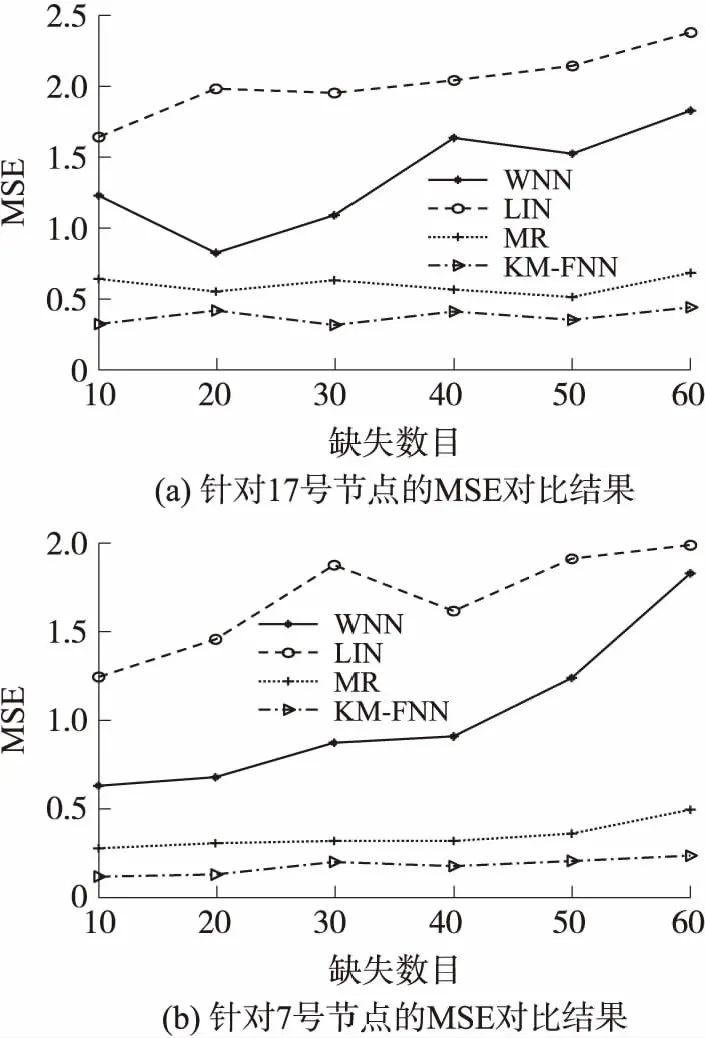
图7 四种算法的MSE对比实验

由图7可知,LIN的MSE最高,这是由于LIN是基于节点的时间相关性,其适应于较短时间间隔内的数据呈平稳变化的场景下,而所用的数据集经过二次采样,更加大了时间间隔。因此,该方法针对17号节点和7号节点的数据重建精度最低。MR基于传感器节点的空间相关性,对缺失数据的估计相对较为精准,具有良好的数据重建精度。相对于WNN算法,KM-FNN具有极强的自适应性能,因此其模型精度最高。

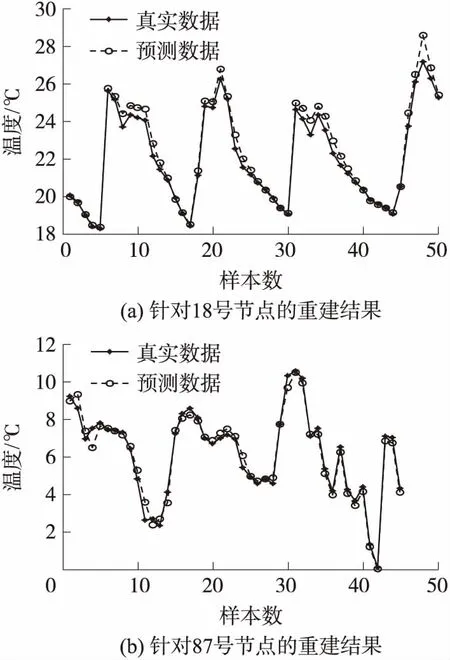
图8 数据重建结果

图8表示数据集Ⅱ下18号节点和数据集Ⅳ下87号节点的数据分别使用KM-FNN重建缺失数据的结果。其中,从18号节点和87号节点的数据集中分别删去50个和45个样本,以便人工模拟数据缺失情况。从图中可以看出,真实数据曲线与预测数据曲线基本保持一致。综上所述,KM-FNN具有精准的数据重建精度。

4 总结

针对无线传感器网络的数据缺失问题,提出了一种分簇式无线传感器网络缺失数据自适应重建算法KM-FNN。该算法使用模糊神经网络模型重建节点的缺失数据,并引入滑动窗口机制与K-均值算法来模拟模型的自适应机制。仿真实验表明,与以往同类算法相比,KM-FNN算法具有更好的缺失数据的重建性能,使用该算法避免了累积误差对无线传感器网络数据的影响,从而有效地提高了数据的可靠性。由于真实环境中的簇头节点的计算能力较低、能量有限。KM-FNN无法烧写入簇头节点中。今后将尝试对KM-FNN进行优化,并将其应用于真实的WSN中,以验证本算法的实用价值。