织物折皱回复性表征方法研究进展
2019-09-21赵娜娜丁雪梅
赵娜娜,丁雪梅
(1.东华大学 服装与艺术设计学院,上海 200051; 2.东华大学 现代服装设计与技术教育部重点实验室,上海 200051)
织物在日常的服用和保管过程中受到外力的作用产生变形而形成折皱,这直接影响了其服用性能和美观性,而且沿着折痕方向易产生磨损,加速了织物的损坏。因此,对织物折皱回复性能的研究是非常必要的。织物的折皱回复性能也称为织物抗皱性,指在一定条件下去除使织物产生折痕的外力后,织物回复到初始状态的能力[1]。织物折皱回复性能受到相当多因素的影响且很复杂,例如直接影响织物折皱回复性的因素有:纱线刚度、纱线交织弯曲程度、织造工艺等[2-3]。前人以表观现象和理论模型为出发点对织物折皱的弯曲和回复机制进行研究,并且运用力学、几何学的方法分析织物折皱回复性能[4-5]。目前国内外对此的研究主要分直接测试和模型表征2种。直接测试包括主观评价法和仪器测量法;模型表征法主要包括图像处理法、建立折皱回复角与物理力学性能相关的回归模型,与力学、形变几何学相关的能量消耗模型等。
织物折皱回复性能与其所处环境中热、湿、机械力等因素密切相关,当前对织物折皱形变回复的研究尚不完善,需考虑各个因素对织物折皱回复的影响,从而形成严谨的织物折皱回复理论体系。
1 直接测试法
因织物为柔性纤维材料的片状集合体,且织物折皱产生和回复过程中织物形变的变化相对较小,同时直接测量法往往再现性差,耗时费力,因而直接测试法对于织物折皱回复的测量难以满足当前检测需求。直接测试包括主观评价法和仪器测量法,前者容易受到外部环境和检测评价个体生理、心理因素的影响,精度低;后者采用的实验室常用测试仪器主要包括SDL-M003 A型折皱回复角试验机(英国锡莱国际开发有限公司), YG541E型全自动激光织物折皱弹性测试仪(常州市第一纺织设备有限公司),YG(B)541D-Ⅱ型全自动数字式折皱弹性仪(宁波纺织仪器厂)等。
1.1 主观评级法
1967年美国纺织化学家与印染师协会(AATCC)RA61 技术委员会首次提出主观评级方法,并沿用至今。现有的AATCC 124—2011《织物经反复家庭洗涤后的外观平整度测试方法》标准中通过比照织物与标准样板的相似程度,评级专业人员主观地给出1至5之间的等级数值[6-7],精度到0.5级。图1为织物折皱平整度标准样板,为了区分3级和4级间的折皱跨越,除了5个平整度整数级外,还增加了3.5级,同时该等级一般作为进出口检验的合格阈值[8]。AATCC 124—2011 标准样板见图1。

图1 AATCC 124 标准样板
折皱平整度主观评价法除用于纺织品服装的贸易检测外,在洗护设备(洗涤、烘干、熨烫设备等)及洗涤剂性能评估中,1~2级的出现概率较多,人工评级的精度难以区分洗护设备及洗涤剂产品性能的优劣。类似的主观检测方法标准如ISO 7768—2006《清洗后织物外观的平滑度评定的试验方法》、 GB/T 13769—2009《评定织物经洗涤后外观平整度的试验方法》均参照AATCC制作的标准样板进行主观视觉评价。虽然主观评级方法应用范围广但其存在着诸多缺陷,如精度低、稳定性差、耗时长、成本高;且由于检测评价人员个体生理、心理之间存在着差异,评价结果离散较大,且3级以上折皱数量形态难以区分[9],影响了结果的准确性。
1.2 仪器测量法
1.2.1 SDL-M003 A 型折皱回复角试验机
SDL-M003 A型折皱回复角试验机参照AATCC66—2008《机织物折皱回复性的测定:回复角法》要求进行测试,主要由刻有角度的圆盘测量装置和负载压重装置组成,配置有3种负荷,规格为500、1 019、2 000 g[10]。SDL-M003 A 折皱回复角试验机及实验过程见图2。

图2 SDL-M003 A 折皱回复角试验机及实验过程
实验开始时样品需沿长边对折,保证样品两端对齐,为了保证测试结果的准确性,测试全程需用镊子夹持试样,快速将负载压重装置放上折叠的样品上并开始计时,持续(300±5) s后将试样移到刻度盘的试样夹上,样品一端夹入试样夹,另一端自由悬垂,使样品折痕线与试验机刻度盘的轴心点垂直。夹持(300±5) s后,人工读出折皱回复角度数。
1.2.2 YG541E型全自动激光折皱弹性测试仪
YG541E型全自动激光织物折皱弹性测试仪按照GB/T 3819—1997《纺织品 织物折痕回复性的测定 回复角法》的要求进行测试[8],实验时,依次夹入10个试样,并压上有机玻璃压片,其采用小车自动定位,自动采样,每隔15 s依次有一个重锤落下,5 min后重锤依次弹开,小车从左到右移动依次采集10个试样的急弹和缓弹角度[11]。YG541E型全自动激光织物折皱弹性测试仪工作结构原理见图3。
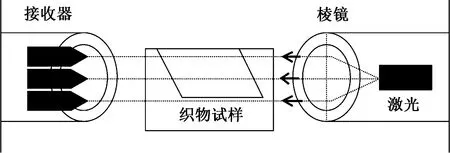
图3 YG541E 型全自动激光织物折皱弹测试仪工作原理图
综上,YG541E型全自动激光织物折皱弹性测试仪测试过程自动化程度高,但由于各个重锤按压力度不均等、试样折叠翼不易弹开,造成其测试结果波动性大,数据准确性和一致性较低;SDL-M003 A 型折皱回复角试验机测试数据波动较小,结果较稳定,但人工重复性操作步骤多,耗时长,效率低。
2 模型表征法
织物折皱形成,从宏观上表现为织物表面上下凹凸不平,基于此研究主要集中在对织物折皱图像处理技术的开发应用;从微观上看,织物内部纤维、纱线、组织结构等织物内部性能与折皱形成呈现复杂关系,对此一部分学者通过建立模型来表征折皱。
2.1 图像处理法
当前纺织品特性的分析已大规模使用成像技术,相当多测量仪器是用图像分析技术开发的。许多学者试图用数字图像处理技术来开发切实可靠的评估织物折皱仪器方法。
通过表征表面和阴影面积比[12]和使用具有分形几何尺寸的立体成像[13]来确定织物平滑度。此外,利用激光探头测量织物表面的物理特征,如表面高度变化[14-15]。AMIRBAYAT等[16]以及SU等[17]提出了一种激光线三角测量法来描述起皱织物的三维表面数据,然后,建立神经网络来执行关于视觉标准的皱纹分类[18]。线性激光轮廓仪和三维投影网格技术[14、19]也是用于评估织物光滑度外观,该研究旨在提取织物的表面轮廓和三维形貌以表征皱纹。HU等[20]和 YANG等[21]开发了一种光度立体方法,其中连续图像之间的入射照明方向是变化的,同时保持观看方向恒定。
以上所有客观方法都使用数字图像处理技术,但所有这些系统都是基于AATCC折皱回复测试。RAJA ZAOUALI等[22]提出了一种由法国方法(Cylinder Creux)产生的多方向“真实”折皱的客观评估方法。图像分析用于定义皱纹的基本特征,如皱纹强度平均值,皱纹表面粗糙度,皱纹体积和皱纹密度。折皱分析步骤见图4。
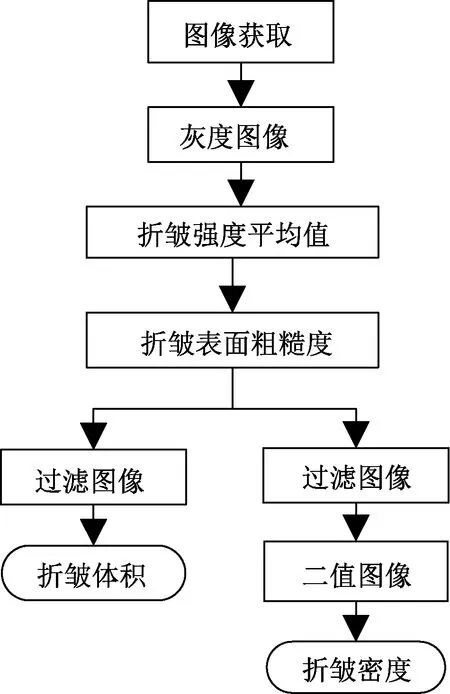
图4 折皱分析步骤
最终得出折皱级别线性回归方程为:
WR=-3.51+0.038M-0.193R-0.324D
(1)
式中:WR为折皱等级;M为折皱强度平均值,mm;R为折皱表面粗糙度,mm;D为折皱的密度。
该统计模型R2=97.3%,呈现良好的线性关系,图像处理确定的参数客观评价织物折皱的模型总体上是显著的。
2.2 折皱模型
织物折皱的形成是因为织物弯曲时纺织材料所表现的黏弹性和纺织纤维的内摩擦性。然而织物的弯曲性能与纤维的弯曲性能、纱线和织物结构以及织物后整理等因素有关且关系相当复杂[23]。目前织物折皱模型集中在2方面:建立织物折皱回复角与织物物理力学参数之间的线性回归方程和折皱回复过程中对折皱回复力与折皱弯曲形变建立能量耗散模型。
2.2.1 力学指标回归模型
石风俊等[24]通过研究织物折皱的力学关系,通过实验结果计算出织物折皱模型参数,从而得出折皱回复角;XIA等[25]建立了织物的应变曲线与织物折皱之间的回归方程,确立了织物折皱回复性与织物应变曲线的关系;张晓婷等[26]找出了织物物理性能与折皱回复性之间的线性关系,采用织物力学性能指标表示其折皱回复角的回归方程;赵立环等[27]在KES系统原有力学性能指标基础上指出折皱回复性的改善方法并引入2个新指标:残余弯曲曲率和残余剪切变形,分析了织物折皱回复角与各力学性能指标间的相关性,在精确表征织物折皱回复角的回归方程中是不可忽略的。
2.2.2 形变能量耗散模型
折皱织物的变形需要外力的作用,因此折皱形成过程中大部分能量作为弹性变形的能量存储在织物中。外力消除后,织物趋于恢复到原来的形状[28]。施加外力时,纯弹性材料不会消耗能量,黏弹性材料会失去一部分储存的能量,折皱形成的关键就是能量的消耗。
许多使用能量方法得出的理论公式通常太过复杂,无法直接应用[29]。WANG等[30]提出了一种基于能量的方法来模拟不同的皱纹形状,以表示非刚性物体的不同材料属性。此外,石风俊[31]基于纺织材料的弹性回复性能及织物的内摩擦作用,研究了在较小作用下织物的折皱弯曲与回复性能,此时织物产生的形变主要是弹性形变,因此可以把织物看成是一个具有内摩擦约束的弹性条,其流变模型由一个虎克弹簧和一个摩擦元件并联组成,简称Voigt或者Kelvin模型。分析毛及毛/涤织物在折皱回复过程中回复力与折皱弯曲形变的关系。为简化计算,假定织物压缩后的轮廓为跑道型,即与上下压板的接触部分为直线,织物弯曲部分为半圆形。Voigt或者Kelvin模型见图5,织物折皱回复变形的几何形状见图6。
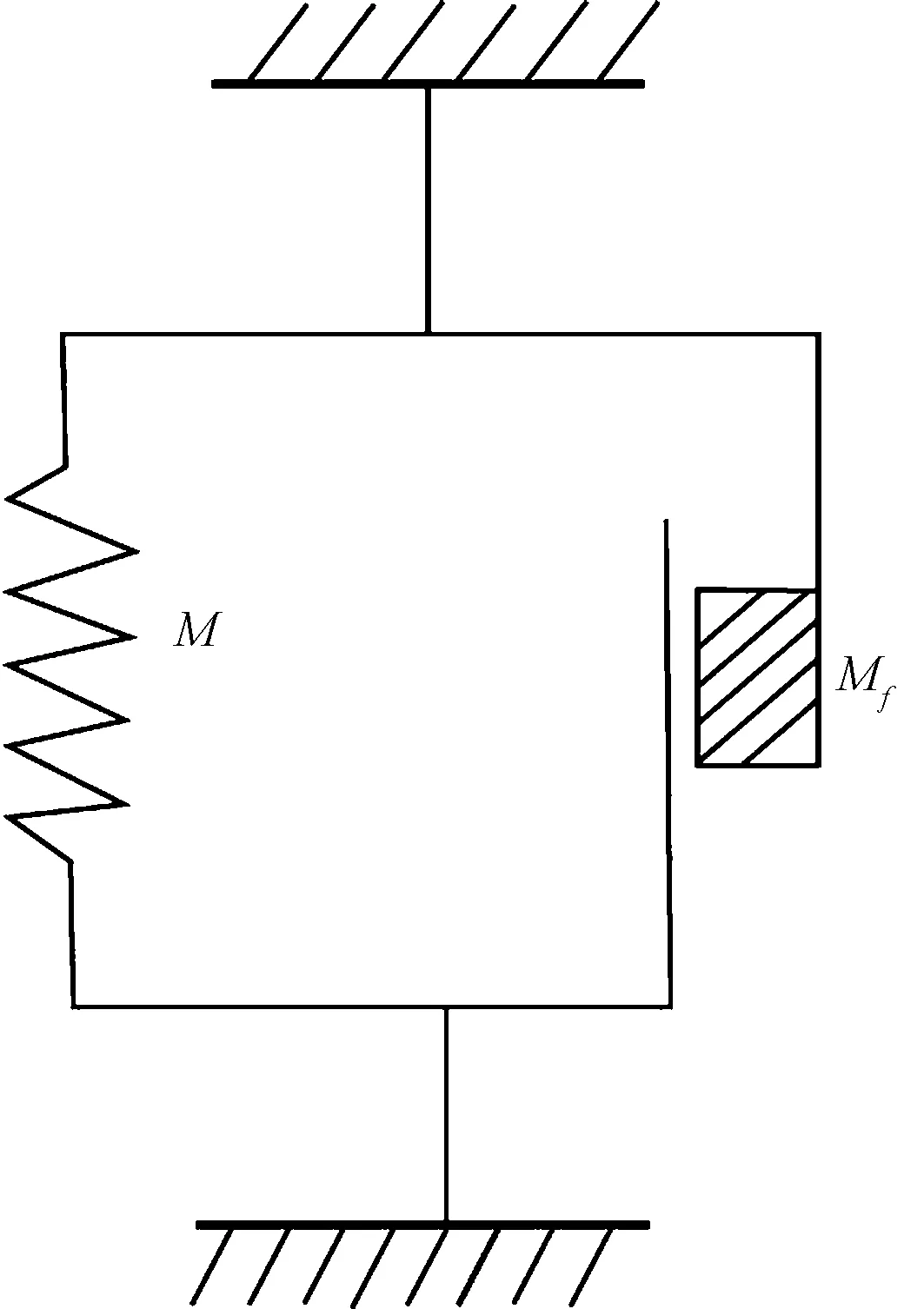
M为织物弯矩;Mf为摩擦约束力偶。图5 虎克弹簧与摩擦元件并联模型
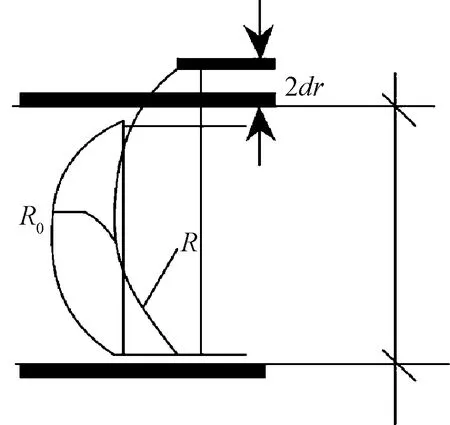
R为回复前曲率半径;R0为回复后曲率半径;2dr为回复后两平行面间隔差。图6 织物折皱回复变形的几何形状

(2)
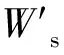
通过对能量Ws微分可得到回复力。然而该模型忽略了塑性变形,纺织纤维具有黏弹性质,即使对于弹性性能较好的毛织物、毛/涤织物,仍然存在塑性形变,所以RAJA等[32]在折皱形变回复和能量耗散之间建立能量模型更加严谨且符合织物折皱回复的真实行为,是由Kelvin模型与Maxwell模型串联构成Burger′s模型,其重点研究黏弹性行为的能量建模,包括对瞬间形变、缓弹性形变和塑形形变,同时深入研究了反复起皱疲劳测试的能量耗散规律,Burger′s模型见图7。
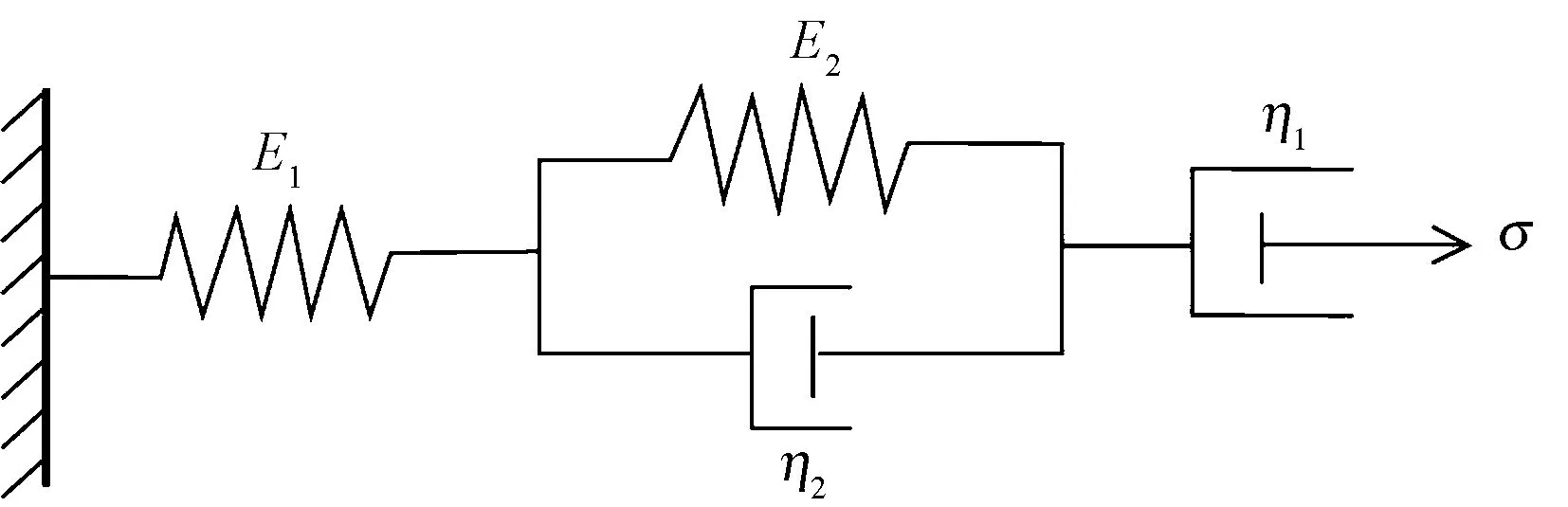
σ为持续外力,N;E1、E2为弹性常数,N/mm;η1、η2为阻尼系数,(N·s)/mm。图7 Burger′s模型
根据变形热力学中表示的能量平衡和忽略热机械耦合,得到能量平衡公式[33]:
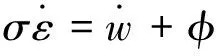
(3)
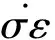
最终推导得出:
(4)
式中:σ0为持续外力,N;E2为弹性常数,N/mm;η2为阻尼系数,(N·s)/mm;t为折皱回复时间,min;t1表示外力施加时间(1 min);E2、η2流变学参数根据不同实验织物的实验数据确定得到[34]。
结果表明,能量消耗越低,织物越能够回复到初始状态,残余变形越少。此外,反复起皱后疲劳循环次数的增加导致残余变形和永久变形的增加。
综上,图像处理技术在织物折皱分析方面得以应用,但是多数研究仍旧是在折皱评价标准基础上进行测量研究的,且图像法研究并不成熟,应用具有一定局限性。所以学者们通过建立折皱模型试图更加准确的表示折皱的回复行为,然而力学指标模型需要测量多个力学指标,较直观测量法准确,但工作量大且复杂。对于折皱能量模型,主要分2个方向,其一是通过折皱回复力求得折皱回复能量,采用开尔文流变模型对弹性性能好的织物在小形变情况下预测并分析织物折皱回复性能各指标。其二在考虑织物的黏弹性和塑性前提下,采用Burger′s模型对织物在较大折皱力情况下的折皱和回复进行预测分析,当前此类模型多为通过形变与能量关系反应折皱回复过程,但为了应用此模型,需要大量实验测量不同面料的流变参数。
3 结束语
织物折皱回复是评判织物服用性能的重要指标之一,因此准确评价表征织物折皱回复性具有重要意义。目前针对织物折皱回复性方面的研究层出不穷,结果也不尽相同。织物折皱形变及回复是一个相当复杂的过程,受到织物内在属性和外在环境因素共同影响,本文研究在统一外界环境为标准大气下进行,但只讨论了织物折皱形变与织物本身内在因素之间的关系,在日常生活中,织物折皱所处环境时刻都在变化,比如洗涤、烘干、蒸汽熨烫过程,织物折皱形变的回复过程未见研究,因此目前关于外界环境中的热、湿、机械力耦合作用下织物折皱形变的回复研究尚不完善,对于其评价表征方法,需全面考虑各影响因素,建立完善的织物折皱评价模型和体系。
