基于支持向量机的精纺毛织物透气性预测
2019-09-21邵景峰王希尧
邵景峰,王希尧
(西安工程大学 管理学院,陕西 西安 710048)
织物透气性与其纱线材料的相应属性存在较强的关联性,随着纱线生产制备工艺越来越复杂,其纱线指标属性越来越多,导致织物透气性的各个影响因素之间存在非线性关系,从而难以达到精准预测[1-2]。
国外学者对于织物透气性预测的研究主要体现在神经网络法和回归分析法方面,得到了织物物理属性与织物透气性对应关系,并建立了相应的回归模型,实现织物透气性的预测。ERENLER 等[3]使用4层BP神经网络,其中每个隐层网络包含5个神经元,在回归程度为R=0.993 66的情况下,对织物的透气性得到较好的预测,但是模型存在训练时间过长的问题;MATUSIAK[4]在其建立的多个预测模型中,其中每个隐层网络分别包含2、3和4个神经元,最后得到的4个模型分别适合不同材料的透气性预测,但其模型泛化能力不足;ÇELIK[5]建立了织物组织结构与其透气性之间联系,并得到织物厚度与孔隙率间存在强烈的正相关关系。结果表明,孔隙率的增加弥补了织物厚度对织物透气性的负面影响;AFZAL等[6]运用统计回归模型,研究探讨了织物毛圈长度、面密度、厚度与透气性能之间的对应关系,运用灵敏度分析定量解释了各个因素对透气性的影响,得到毛圈长度是最主要的影响因素。
在我国,众多学者利用神经网络法、灰色系统理论、因子分析法和主成分分析法等方法来探索织物透气性预测。徐广标等[7]构建了织物透气性能与织物结构参数之间的3层BP神经网络,将织物透气量的预测误差率控制在3.0%~ 24.2%。黄紫娟等[8]通过测试8种毛织物的结构参数与透气性能应用灰色系统理论,通过线性回归模型对毛织物透气量与其主要影响因素进行定量分析,得到织物的经向密度和纬向密度与透气量均呈负线性相关。佐同林等[9]采用因子分析方法对20种精纺毛织物的 12个与透气性密切相关的结构参数进行优化提取,得到12个结构参数可以综合成4个因子变量,虽取得了降维效果但并没有明确得到织物参数与透气性的相关关系。佐同林等[10]利用主成分分析方法对织物基本结构参数进行降维处理,得到4个互相独立的主成分。以主成分为自变量,透气性为因变量,采用回归分析的方法建立了透气性与提取主成分的关系模型。
通过文献回顾发现,国内外学者研究了织物物理属性与织物透气性对应关系,并建立了相应的回归模型,实现织物透气性的预测,但都存在训练时间过长、样本量需求较高等问题。其中原因在于:一方面,采用神经网络方法当训练样本数较少时,容易陷入局部最优解,导致模型泛化性能不足。另一方面,由于实际一个变量受多因素综合影响,回归分析法不能给出具体的预测模型,导致因子的多样性和某些因子的不可测性。针对上述问题,本文将采用支持向量机(SVM)算法,构建织物的结构参数与织物透气性能的SVM模型,从而达到对织物的透气量进行预测与评价的目的。
1 精纺毛织物透气性回归算法
1.1 预测原理
现有的支持向量机预测流程图如图1所示,本文研究在数据收集阶段,实验数据来自文献[7]。在收集到足够有效的数据基础上,选取适当的输入与输出指标。在划分训练集与测试集阶段,利用实验所用的34组试样,随机选择27组作为训练样本,剩下的7组作为预测样本。在预处理阶段,为避免量纲对实验结果的影响,消除不同变量取值范围间的巨大悬殊,对试样中数据做标准化归一化预处理。并选择合适的核函数,对关键参数(C,σ)进行初始化。最后将训练样本输入支持向量机,通过对SVM模型的多次迭代训练下完成对模型关键参数的调优。根据测试集表现的预测结果,对模型的建模过程和训练进行优化修改,最终得到预测精度稳定且高效的SVM模型,使其对预测精纺毛织物材料透气性具有合理性与可行性。

图1 精纺毛织物透气性能预测流程图
1.2 支持向量机基本思想
支持向量机算法相比于BP神经网络法和因子分析法、主成分分析法等回归分析法,其可以在较少的样本量和复杂的模型下,寻找到最佳学习能力,从而获得最好的泛化能力,它能保证找到的极值解是全局最优解而非局部最小值[11]。
SVM可作为一个特殊的BP神经网络,它可以自适应地选择中间层的神经元个数以及学习步长,不仅克服了一般BP神经网络凭借经验选取中间层神经元个数及步长的缺点,而且避免了基于梯度下降法所固有的局域最小[12]。其基本结构如图2 所示。
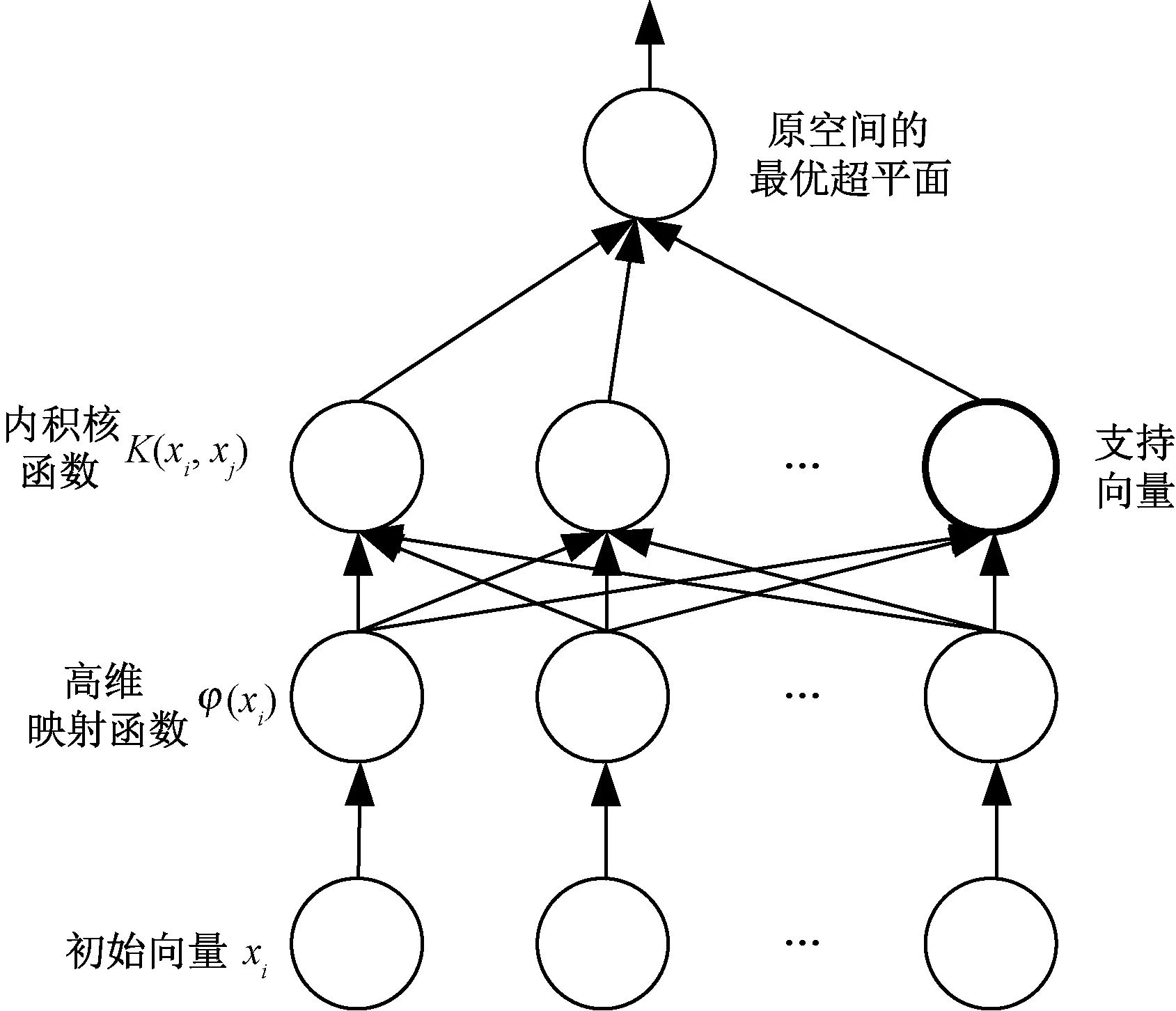
图2 SVM的结构示意图
1.3 透气性回归算法
在SVM函数拟合中,本文模型的为f(x),输入为x,模型可表示为
f(x)=ω·φ(x)+b
(1)
式中:x为织物密度、纱线直径等输入特征向量;f(x)为精纺毛织物透气量;φ(x)为映射到高维特征空间的非线性函数;ω为超平面的权重向量;b为最优超平面偏移量,即此回归模型的偏置系数。
因为数据的线性不可分性,需要通过优化软间隔和增加松弛变量的方法来实现。目标函数式(1)可转化为求解式(2)的凸约束条件下的2次凸规划问题:
(2)
满足约束条件:
式中:ε为允许的精度参数;C为惩罚因子一般为正数,表示结果超出样本误差时的惩罚程度;ξi和ξi*为松弛变量,确保式(2)在更大的可行域内有解。
织物密度、纱线直径等输入特征向量xi被φ(x)映射到一个高维特征空间后,SVM算法将在这个高维特征空间中找到一个函数间隔最大的线性超平面来对数据进行分类。
为求解变量式(1)ω和b的最优解。引入核函数K(x,y),本文选取径向基函数作为核函数:
(3)
根据KKT定理,可得回归函数的表达式为
(4)
偏置系数b可按下式计算:
(5)

2 精纺毛织物透气性回归模型
2.1 输入输出指标选取
织物透气性作为人体衣着舒适性的重要指标之一,其处在多因素相互耦合作用下。织物和纱线的多个参数属性都会对织物透气性能产生影响。
织物的透气性表示在一定压差下通过织物后气流的速度,与织物的舒适性密切相关。织物的透气性直接取决于织物间空隙的规格与数量,而这又与纱线纤维的几何结构密切有关。一般情况下,纱线越粗、织物厚度越小、织物的透气性越大;线密度相同的织物中,随着经纬向密度的增加,织物的透气性会降低;异形截面纤维织物的透气性要明显优于圆形截面纤维织物[13]。
基于此,从织物参数、纱线性能等方面,选取织物密度(根/(10 cm))、纱线直径(mm)、平均浮长、面密度(g/m2)、总紧度(%)、特质捻系数、空隙透气量(L/m2·s)、纤维平均直径(μm)作为输入特征向量,即X=(x1,x2,x3,x4,x5,x6,x7,x8)8个指标作为SVM预测模型的输入指标,选取输出特征向量Y=(y)即织物透气量作为SVM预测模型的输出指标。
2.2 基于SVM的回归模型的建模
2.2.1 数据标准化处理
根据2.1节的输入输出指标选取,因具有不同的量纲和数量级,如果直接将原始指标值进行带入模型分析,数值较高的指标在综合分析中的作用将会掩盖住相对削弱数值水平较低指标的作用。因此,为了保证实验结果的可靠与准确,对原始输入输出指标数据进行标准化处理。
(6)
式中:max(X)为数据集中的最大值;min(X)为数据集中的最小值。
通过对数据的标准化处理后,将训练好对的数据映射到区间[0,1],再进行后续的测评预测,以达到提升模型的预测精度的效果。
2.2.2 回归模型的关键参数
SVM回归模型的预测精度取决于其模型核函数选择及其参数设置。本文所建立的SVM模型有2项关键参数:惩罚因子C和核函数σ。其中C用来控制SVM回归的拟合误差,当C值越大时拟合误差就会越小,模型训练时间也就越长,但是过大的σ会导致过拟合现象的出现。σ是径向基核函数(RBF)的核参数,表示该核函数的宽度、核函数、映射函数和特征子空间是相互一一对应的,核函数确定的同时相应的映射函数和特征子空间也随之确定。特征子空间的维数表示在此空间中能够构造的最优分类面和最大VC维,即是最优分类面所达到的最小分类误差。当σ越小时,拟合误差越小,模型训练时间也就变长。但是,σ过小会过拟合现象的出现难以避免。所以,训练模型中的惩罚因子C和核函数σ选择是十分重要的。
2.2.3 基于SVM的回归预测模型
根据2.2对于算法的阐述,最终确立的模型如下:
(7)
2.2.4 回归模型训练与测试
对归一化后数据代入基于SVM的精纺毛织物透气性预测模型进行训练和测试。实验试样为34组,随机选择27组作为训练样本,剩下的7组作为预测样本。在训练过程中,对所阐述的关键参数采用网格搜索法与交叉验证法确定最优参数[14]。
在得到训练好的精纺毛织物透气性能预测模型后,利用测试集数据得到预测结果,通过不同的训练数据集和测试数据集比例评定模型的泛化性能。并与BP神经网络模型进行对比分析,比较2个模型预测精度。
3 模型验证与评价
3.1 实验环境与设计
在Windows7操作系统下,利用Eclipse、Anaconda、Pydev软件搭建实验仿真平台,对基于SVM的精纺毛织物透气性能预测模型进行仿真实验。为了验证模型预测的泛化性,采用相同的数据集合优化参数,分别对不同的训练数据集和测试数据集比例进行训练的测试。为了验证模型预测的准确性,采用相同的数据集分别对基于SVM和基于BP神经网络的精纺毛织物透气性预测模型进行训练和测试。
3.2 数据的准备与处理
在3.1节的实验环境下,选取文献[7]实验数据,如表1所示。根据2.1节对于模型输入输出指标的选取,搜集了具有代表性的34种精纺毛型织物试样,其中4种纯毛织物,2种毛/粘混纺织物,其他为毛/涤混纺织物,实测织物结构参数及利用哈根-伯肃叶(Hagen-Poiseuille)公式计算织物纱线间空隙透气量[7]。
根据式(6)对所选择数据进行标准化处理后,带入SVM进行学习训练。
3.3 SVM模型参数寻优
实验数据在核函数的选取上,采用的径向基函数作为基于SVM的精纺毛织物透气性回归模型。学习训练过程通过Eclipse、Anaconda、Pydev等软件实现。为了使模型具有良好的预测能力,需要寻找合适的SVM计算参数[15-16]。学习训练时需要确定:惩罚因子C和核函数σ2个参数,采用网格搜索法与交叉验证法确定。模型关键参数学习训练过程如表2所示。在初始化范围下,采用网格搜索法搜索最佳参数所在区间,在学习训练中利用前一步得到的区间交叉验证得到最佳参数。
3.4 SVM模型泛化性分析
为了进一步评估SVM模型在精纺毛织物透气性上预测的泛化性能,从织物样本中随机地抽取数据纳入训练集和测试集。在每次试验中,34-K个样本作为训练数据以确定最优模型,剩余K个样本作为测试数据检验模型的泛化能力。为了便于观察模型的泛化能力,引入回归误差率(R)检验:
(8)
式中:PV为回归模型的预测值;TV为实际值;R为模型误差率。
可以看出,R越低表示模型预测更加准确。本文实验了10个不同的K值(K=1,2,3,4,5,6,7,8,9,10),每个K值重复实验10次,每次都随机地选取实验所需训练集数据与测试集数据,误差率计算10次实验的均值。
SVM预测的整体误差率如图3所示。可以看出,当K值为1~5时,模型的平均误差率稳定在0.04%以内,K值为6~7时模型的平均误差率稳定在0.04%~0.05%以内,当K值大于7时,误差率骤然上升。原因是样本数据只有34组,当测试数据与训练数据样本比例小于2∶8时,模型的学习样本不足,预测能力不够。当测试数据与训练数据样本比例大于2∶8时,模型过度学习,泛化能力不足。但在合理的测试数据与训练数据样本比例下(2∶8),即27个训练样本、7个测试样本,其泛化性能是稳定的。

表1 34种精纺毛型织物结构参数表
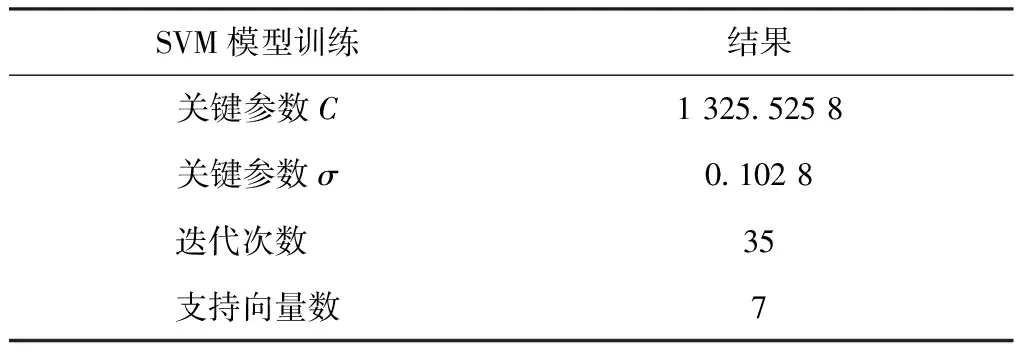
表2 模型关键参数学习训练
3.5 SVM模型与BP模型预测结果分析
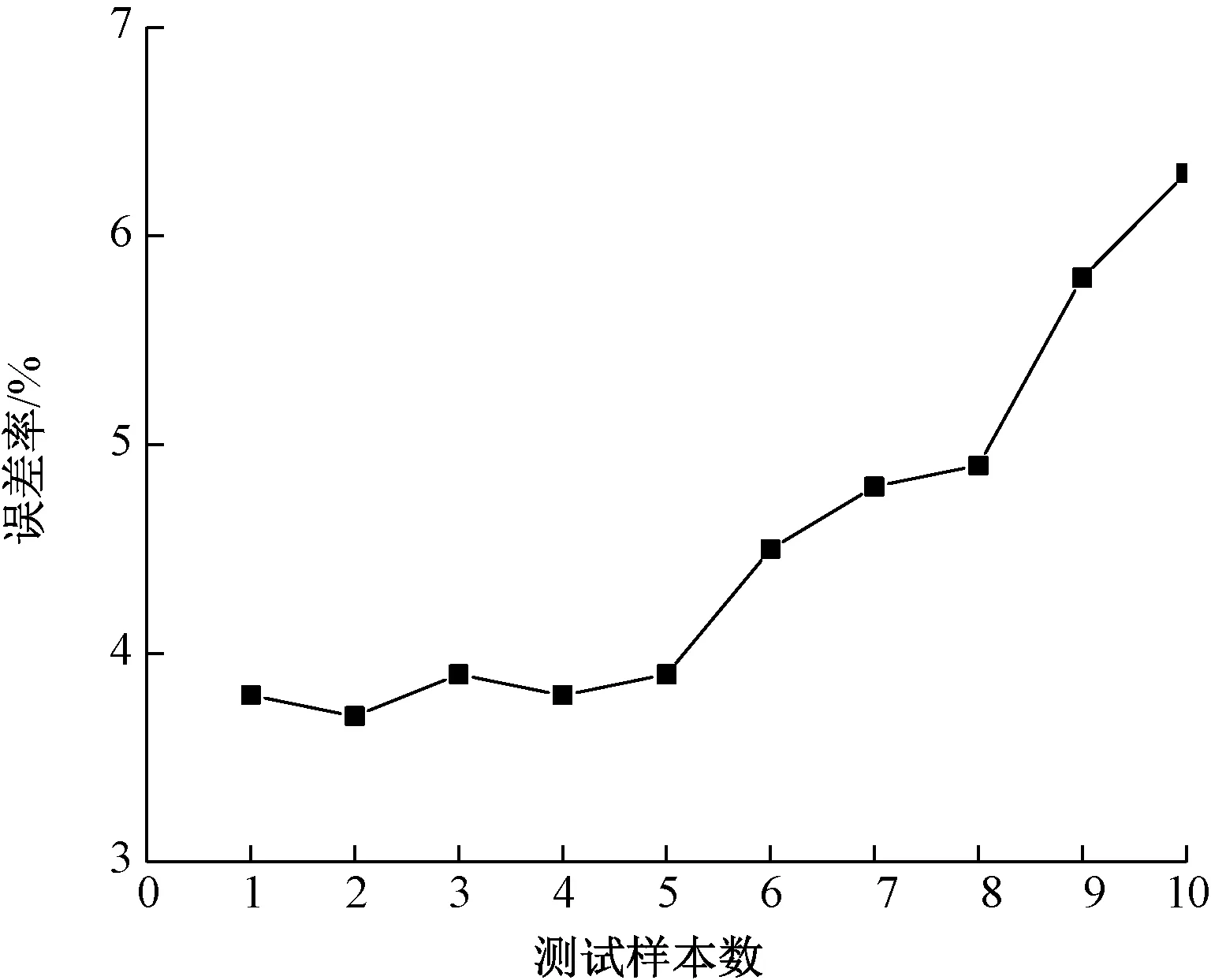
图3 SVM预测整体误差率
以拟合优度R2和相对误差为评价指标,对比SVM与BP神经网络的模型预测效果,为比较SVM与BP神经网络的预测效果,选取了相同训练集与测试集,如表3和图4所示。SVM回归模型的拟合优度最接近1(0.998 6),在3层的BP神经网络回归模型下,实验平均预测误差达到7%。v-SVM精纺毛织物透气性回归模型在参数C=1 325.525 8和σ=0.102 8的情况下,取得了较好预测结果,实验平均误差为3.7%(小于4%)。可以看到SVM回归模型的准确性明显优于BP神经网络。不仅对学习样本的拟合度高,并且评估预测结果与实际结果非常接近。

表3 SVM模型与BP模型预测误差比较

图4 SVM与BP模型实际值与预测值比较
BP神经网络回归模型需要设定很多初始参数如各个神经元权值、偏差、学习率、各个隐藏层神经元个数,并且这些自由参数设置直接影响到其预测准确性。因此在实际应用中为获得具有最佳泛化性能模型,需要选用较大样本量来进行训练与测试。与之相对应的是,SVM回归模型只需要通过交叉检验和网格搜索法,确定C和σ2个参数,即在模型训练测试过程中,相比于BP神经网络,SVM回归模型要简便许多。而且,在选取相同的测试试样下,SVM回归模型的预测结果明显优于BP神经网络。
3.6 鲁棒性分析
本文通过对2种模型预测相对误差的极差分析,来分析比较2种模型预测的稳健度。
通过表4可得到,SVM预测模型的相对误差分布区间为[2.27%,5.21%],其极差为5.21%-2.27%=2.94%。相应地,BP预测模型的相对误差分布区间为[5.08%,9.96%],其极差为9.96%-5.08%=4.88%。
即通过以上分析,有“基于BP模型预测的相对误差”的极差相较于“基于SVM模型预测的相对误差”的极差要大70.0%。因此,基于SVM的预测模型的预测精度更稳健。
4 结 论
本文利用基于SVM的精纺毛织物透气性回归模型,实验从34组样本中,随机选择27组作为训练样本,7组作为预测样本,对精纺毛织物透气性能做了预测,较好地得到了织物结构因素参数与其透气性能之间的非线性关系。可得出以下结论:
①相比BP模型,SVM 模型有较强的非线性关系学习能力和良好的泛化能力,较好地解决了训练时间过长、样本需求量较高等问题。
②训练数据集与测试数据集比例在8∶2时,SVM模型获得更好的预测性能。
③基于SVM的精纺毛织物透气性回归模型,拟合优度为99.86%,平均预测误差为4%。本文模型可以较为高效、精准地做出精纺毛织物透气性预测。
