基于模型预测控制的风电机组载荷控制

曹松青，郝万君*，陈歆婧，王 飞，王 昊，孙志辉

（1.苏州科技大学 电子与信息工程学院，江苏 苏州 215009；2.吉林欧科自动化设备有限公司，吉林省 吉林市 132021）

随着风电机组向着大型化方向不断发展，风轮直径和扫略面积不断增大，机组的疲劳载荷也相应地增加[1-2]，除了基本的功率控制需求，载荷控制也逐渐成为机组控制的重要组成部分[3]。由于独立变桨距控制可以有效解决桨叶和塔架等部件的载荷在时间和空间上的不均匀问题[4]，因此，可以用独立变桨调节来减小叶根挥舞弯矩[5]，实现载荷控制。

在独立变桨距控制方面，近年来国内外学者进行了大量研究。文献[4，6]提出了基于前馈-反馈结构的LQG 独立变桨距控制，可以很好地减小不平衡载荷。文献[7]引入了带增益调度的统一变桨距控制，在此基础上附加基于LQR 的独立变桨距控制，在稳定输出功率的同时也有效降低了零部件的疲劳载荷。然而，LQG/LQR 方法的优化是一次离线进行，难以顾及不确定性的影响，从而难以保证全局最优。文献[8－9]分别提出基于径向基函数（RBF）神经网络PID 的独立变桨控制和基于神经网络模型的预测自适应PID 控制策略，虽然能分别降低俯仰载荷和偏航载荷，但忽略了d 轴载荷控制和q 轴载荷控制之间的耦合关系，难以实现真正意义上的最优控制。

为了有效减小轮毂中心的俯仰力矩和偏航力矩，笔者提出了高风速区大型风电机组的独立变桨距模型预测控制（MPC）方法，在预测输出和目标函数中考虑了随机风速的扰动，并对桨距角的大小和变化率施加约束，利用Matlab/Simulink 软件搭建模型，并以某型号的5 MW 风电机组为研究对象进行仿真。仿真结果表明，与PI 控制、LQG 控制相比，该方法可以更有效地抑制俯仰力矩和偏航力矩，更适合于大型风电机组的独立变桨距载荷控制。

1 独立变桨距系统模型

风电机组独立变桨系统的模型主要由风轮运动方程和塔架运动方程组成，旋转坐标系上的风轮运动方程可以表示为[10]

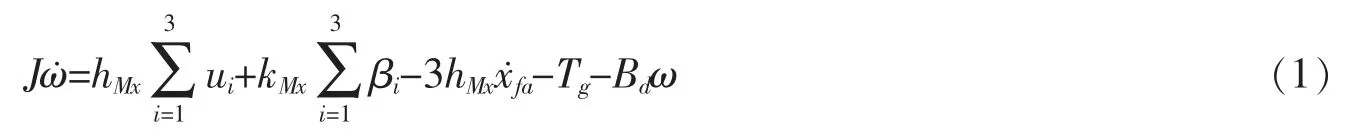
塔架前后方向的运动方程可表示为

输出方程可以表示为

式中，ω 为风轮角速度，ui为每个叶片上的等效风速，βi为每个叶片的桨距角，Tg为发电机转矩，J 为风轮与发电机转动惯量之和，Bd为等效阻尼系数，xfa为塔架的俯仰方向的位移，Mzi为叶片根部面外弯曲力矩，Rb为风轮半径，hMx、hFx、hMz、hFz、kMx、kFx、kMz为工作点处线性化后的气动载荷系数。

将Park 变换将旋转坐标系下的线性时变运动方程（1）-（3）转换为轮毂固定坐标系下的线性时不变方程

其中，φ1（t）～φ3（t）为 3 个叶片的方位角。

2 控制器设计

2.1 MPC算法

大型风电机组的独立变桨控制系统是一个复杂的非线性及多变量输入和输出系统[11]，需要对多个目标进行优化，同时内部各系统之间存在相互耦合作用[12]，且系统输出随着运行工况的改变有较大的变化[13]，因此，需要引入较为先进的控制算法[14]。鉴于此，文中拟采用模型预测控制（MPC）来解决高风速区载荷控制问题。MPC 是一种先进的控制工具，可使用内部模型和当前测量值预测系统的未来行为，主要包括预测模型、滚动优化、反馈校正3 个部分[15]。其基本控制流程如图1 所示，图中，ysp为系统的设定输出，yr为参考轨迹，u为控制输入，y 为系统的实际输出，ym为模型输出，yc为预测输出。

图1 MPC 的基本控制流程

2.2 独立变桨距MPC控制

2.2.1 预测模型

为简化控制器的设计和分析，更直观地表示输出与状态之间的关系，令 Dθ=zeros（2，2），Du＝zeros（2，3），则可得风电机组独立变桨距控制系统的状态空间表达的简化形式

式中，B=[BβBu]，u1=[u v]T。

将式（9）离散化得

文中状态x（k）为可测量，所以式（10）可直接作为预测模型使用。

2.2.2 预测输出

设控制时域为 M，预测时域为 P，则由预测模型（10）可以计算出在 u1（k），u1（k+1），···，u1（k+M－1）作用下未来P 个时刻系统的预测状态X（k）和预测输出Ym（k）

文中取控制时域M=5，预测时域P=10。

2.2.3 参考轨迹

由于期望的风电机组的俯仰力矩和偏航力矩为0，所以文中系统的给定输出参考轨迹yr为风力发电系统当前t 时刻的实际输出y 到给定输出ysp的“柔化”过渡过程

式中，0≤λ＜1。

2.2.4 控制器设计

文中所考虑的风电机组的最佳控制问题可以描述如下： 目标是在存在风速干扰的情况下，找到最优控制律u1（·），使目标函数最小化[16]。其中

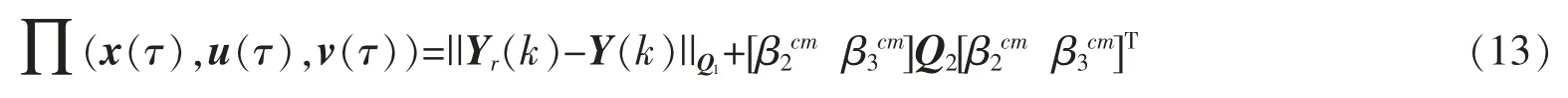
约束条件为

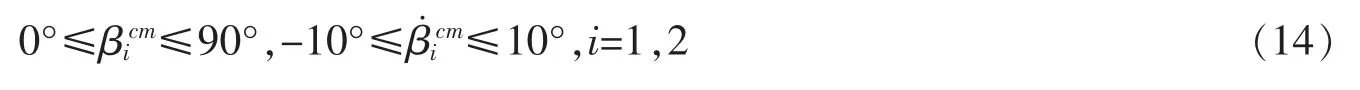
其中，Yr（k）=[yr（k+1），···，yr（k+P）]T为参考轨迹的向量表示为加权矩阵。

式（13）等号右侧第一项用于惩罚风电机组的俯仰力矩、偏航力矩与参考轨迹的偏差，确保跟踪误差最小化；第二项用于优化桨距角的调节，在保证系统控制性能的前提下，尽量减小变桨执行机构的大幅度动作，以降低该机构机械疲劳和延长使用寿命。由于变桨执行机构的调节幅度和调节速率有限，因此，需要对桨距角的大小和变化率施加约束。结合式（11）中的预测输出，可求出最优解的表达式

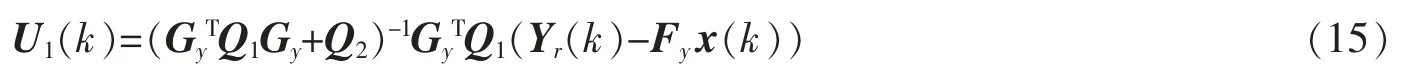
从而可求出即时控制量

按上述方法求出控制量之后，预测控制仅将当前控制量u1（k）作用于风机系统，到下一个采样时刻，优化时域随着时刻的推进同时向前推移，再将k+1 时刻的控制量u1（k+1）作用于风机系统，以此类推，在任一采样时刻r，都将该时刻对应的控制量u1（k+r）作用于风机系统，如此滚动进行，即所谓的“滚动优化”。

2.2.5 反馈校正

在k+1 时刻，检测风机的实际输出y（k+1），并将其与该时刻的预测模型输出ym（k+1|k）作比较，构成输出误差

采用对e（k+1）加权的方式修正对未来其他时刻输出的预测

其中，yc（k+1）=[yc（k+1|k+1） …yc（k+N|k+1）]T，h=[h1…hN]T为权系数组成的 N 维向量。经校正后的 yc（k+1）作为下一时刻的预测初值，由于在k+1 时刻时间基点有变动，预测的未来时间点也将移到k=2，…，k+1+N，所以yc（k+1）的元素需要通过移位才能构成k+1 时刻的初始预测值，故令

由式（18）可得下一时刻的预测输出为

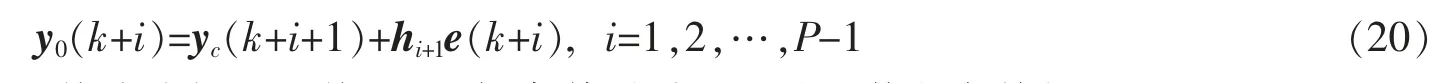
反馈校正的引入，使风机系统成为闭环系统，可以提高其对随机风速干扰的鲁棒性。

3 仿真与分析

为了验证基于MPC 的风力发电机组独立变桨距控制的性能，在Matlab/Simulink 中搭建风力发电系统的模型，然后进行仿真，并与PI 控制和LQG 控制的效果进行对比。仿真结果如图2 所示。

如图2（a）所示，为轮毂处风速v_hub 和三个叶片上的风速v_blade1、v_blade2、v_blade3 的曲线图，额定风速为18 m/s。为了更好地模拟实际情况，三个叶片上的风速均考虑了风剪切效应和塔影效应的影响。

如图2（b）所示，为MPC 与PI 的仿真结果对比。PI 控制器可描述为

式中，KP为比例系数，KI为积分系数。以式（13）作为优化性能指标，通过粒子群自寻优的方法得到俯仰控制器的比例系数为 KP1=-8.263×10－6，积分系数为 KI1=-5.094×10－6，偏航控制器的比例系数为 KP2=-6.503×10－5，积分系数为 KI2=-3.166×10－5。

如图2（c）所示，为MPC 与LQG 的仿真结果对比。LQG 控制的控制律可描述为

以式（13）作为优化性能指标，运用 Matlab 工具箱中的 lqr（）函数计算 LQG 最优反馈增益 K：（K，S，E）=lqr（A，Bu，Q，N），最终求得 K=[-2.762×103，-3.206×103；0，0]。

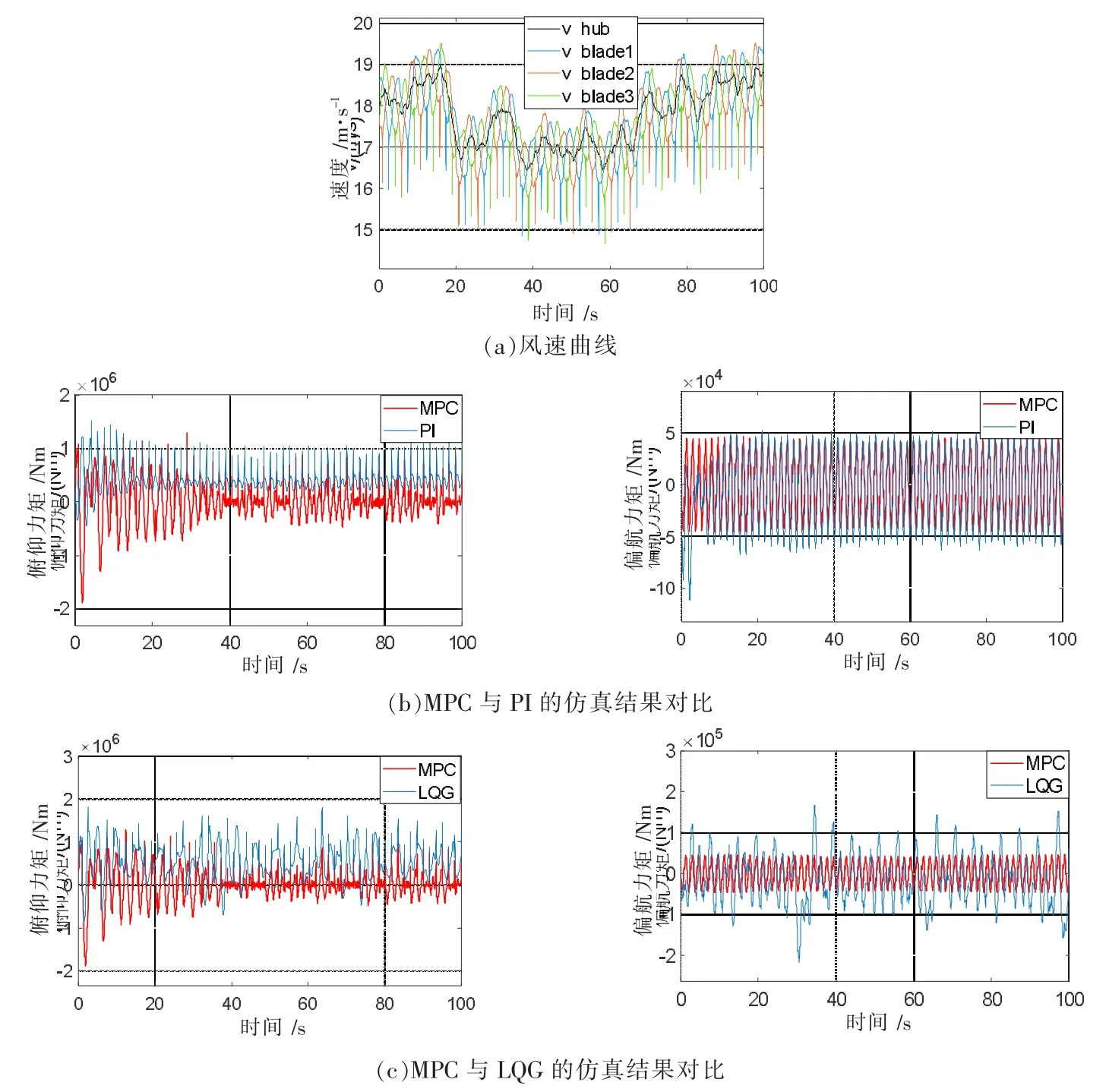
图2 仿真结果

由表1 以及图2（b）、图2（c）可见，采用 PI 控制时平均俯仰力矩 AVG（Mtilt）为 3.768 4×105，偏航力矩的均方差 STD（Myaw）为 3.147 5×104，采用 LQG 控制时平均俯仰力矩为 5.143 6×105，偏航力矩的均方差为6.190 2×104，而采用MPC 时平均俯仰力矩只有-2.768 3×104，偏航力矩的均方差只有 2.653 4×104。与 PI 控制和LQG 控制相比，MPC 能够使俯仰力矩在更接近期望值0 的范围内波动，同时使偏航力矩波动范围更小，说明MPC 可以更好地克服随机风速扰动、具有更强的鲁棒性，在抑制风机不平衡载荷、确保风电机组的平稳运行方面具有显著优势。

表1 三种控制策略的性能对比

4 结语

针对大型风电机组高风速区不平衡载荷的问题，笔者提出模型预测控制策略来改善抑制轮毂中心俯仰力矩和偏航力矩的性能。仿真结果表明，相比于传统的PI 控制和LQG 控制，模型预测控制具有更好的减载效果，更适合大型风电机组的独立变桨距载荷控制。