大数据风控有效吗？——基于统计评分卡与机器学习模型的对比分析

刘志惠，黄志刚，谢合亮

(1.福州大学 经济与管理学院，福建 福州 350108；2.福建商学院 金融学院，福建 福州 350012；3.中央财经大学 统计与数学学院，北京 100081 )

一、引 言

互联网金融是金融和互联网技术的结合，是一种新型金融模式，近几年在中国得到了快速发展，显示出互联网金融巨大的发展潜力。但由于中国征信体系的不完善，给互联网金融行业带来了较大的风险，因此建立一个有效的风控体系是十分必要的。在中国还没建立起一个完善的征信体系之前，信用风险是目前互联网金融行业所面临的最主要的风险。在如何应对信用风险方面，以商业银行为代表的传统金融行业，大多首选采用信用评分卡模型。评分卡模型是指利用大量的历史数据，刻画出消费者的信用、收入水平和支付能力等指标，再把各个指标分成若干个档次，标注各个档次相应的得分，然后计算每个指标的权重，最后算出贷款申请者的信用评分。到目前为止，工业界与学术界对信用评分模型的研究已经有多年的历史，积累了大量的研究成果。

1956年工程师Bill Fair和数学家Earl Isaac创办了FariIsaac公司，该公司利用判别法建立了全球第一个真正具有现代意义的商业化信用评分系统FICO，并且让该系统在全球金融领域得到广泛的应用。之后，Myers等采用判别分析和回归分析法，利用消费者零售信用申请表中的数据对信用风险进行了预测[1]。Orgler将线性回归分析引入到个人消费贷款的信用风险评估，并设计了一套信用评分卡模型，通过模型发现消费者的行为特征比申请表特征更能反映贷款的风险[2]。其他利用线性回归研究信用评分模型的重要研究成果还有Fitzpatrick的研究结论[3]。一般来说，如果将借款人的违约情况用0，1来表示，再利用已有数据建立模型对借款人违约概率进行预测，则线性回归模型就变成了逻辑回归。逻辑回归模型从理论上看比线性回归模型具有更好的解释性，但Wiginton是最早将逻辑回归用于信用评分模型的学者之一，他通过对两种方法信用评分建模的结果进行对比，发现二者的预测效果差别不大[4]。Srinivasan等比较了Bierman和Hausman信用评分模型与逻辑回归模型，认为Bierman和Hausman模型需要在严格的假设条件下才能实现，其预测能力不如逻辑回归模型[5]。

国外学者在信用评分方面利用机器学习的研究也较早。Angelini等利用人工神经网络设计信用风险模型，并分析了意大利的真实商业数据，研究结果表明，神经网络可以建立一套非常有效的信用评分模型[6]。Hand等认为信用评分模型多年来并没有很大进步，大部分的优化工作都集中在对简单判别规则的改进方面，未来的进步应该是出现在更复杂的模型开发方面[7]。Khandani等使用机器学习技术进行消费信贷风险模型的非线性参数预测，利用2005年1月至2009年4月美国主要商业银行客户贷款数据作为分析样本，研究表明机器学习方法比线性回归模型降低了6%～25%的预测误差[8]。Srinivasan等从非参数的角度研究了信用数据的相对有效性，实证结果表明，非参数回归法在信用评分分类模型上更加有效[9]。Jochen Kruppa等比较了随机森林(RF)、K近邻(KNN)和Bagged k近邻(BNN)三种机器学习方法与传统逻辑回归在消费信用评分模型中的效果，通过实验对比发现随机森林算法的分类效果最好[10]。Cuicui Luo等利用深度学习进行信贷违约预测，并与常用的逻辑回归模型、多层感知器和支持向量机模型进行对比，通过实验证明了深度信念网络(DBN)在几种模型中具有最好的预测效果[11]。Bequé等将最近提出的人工神经网络的极限学习算法(ELM)用于消费信贷风险管理，通过实验发现了该算法具有容易使用、计算量小和预测精度高的特点，并通过实证分析证明了ELM方法在信用风险建模方面的价值[12]。

由于国内征信市场还不够完善，截至2018年末有中国人民银行征信报告的人群大约为5亿，而传统的信用评分卡模型的数据来源主要为中国人民银行征信报告，且主要被应用在银行的信用卡业务管理方面，在其他业务领域应用较少。近几年随着大数据时代的到来和国内互联网金融市场的快速发展，一种基于大数据结合人工智能算法的风控模式在国内金融市场中迅速蔓延开来，这种模式迎合了国内个人征信信息缺乏的状态，通过分析借款人的日常生活数据并将数据转换为特征变量，结合机器学习算法预测借款用户的还款风险，这一模式在国内互联网金融市场取得了巨大的成功，学术界对这一创新模式也开展了广泛的研究。如，李萌构造了结合主成分分析法的商业银行信用风险评估的Logit模型，通过实证分析证明了Logit模型具有很高的识别和预测能力，可以作为商业银行信用风险评估的有效工具[13]。刘莉亚从借款人、贷款方案、贷款投向和风险缓释四个维度出发，构建了一套信用评分体系框架，并将该评分系统用于银行个人住房贷款，通过实证分析，验证了模型的有效性[14]。王会娟等利用“人人贷”的数据，以信息不对称作为理论基础，研究了P2P网络借贷平台的信用认证机制对借贷行为的影响，研究发现：借款人信用评级越高，借款成功率越高且借款成本越低，但评级指标的单一性不能很好地刻画借款人风险，还需要完善个人信用评价体系[15]。孙杰等对比了互联网金融与传统银行之间的差异与各自面临的挑战，并从传统银行角度提出了谋求互联网金融与传统银行之间的交集，提出了在大数据时代下银行业应该如何走向成功的思路[16]。巴曙松等认为目前引人注目的大数据风控问题既存在着数据质量的障碍，也存在大数据风控的理论不完善的障碍，并且还有数据保护制度的障碍，而要完善中国的大数据风控，需要金融机构、金融研究部门和监管部门的共同努力[17]。何飞等认为，中国征信系统还不够完善，未来应该从改善信息不对称出发，构建互联网金融系统基础数据库，促进互联网与金融双重属性的深度融合[18]。涂艳等以“拍拍贷”交易数据，建立了逻辑回归、神经网络、支持向量机等机器学习模型预测借款人违约概率，研究表明，随机森林、神经网络与决策树等机器学习算法的预测结果普遍高于传统回归模型[19]。

从以上文献梳理可以看出，传统的信用风险方法在分布假设、线性等方面有严格的假设，这些假设制约了传统方法在度量信用风险的应用。因为在线网络借款数据很难满足传统方法的假设条件。而随着互联网的普及、各种数据的积累、大数据技术的兴起以及机器学习算法(如 XGBoost、深度学习、强化学习等)快速发展，基于多来源多类型数据的机器学习信用风险评分模型逐渐被行业认可，并广泛使用。传统信用风险度量方法主要考虑的是贷款人特征与违约结果之间的强因果关系，而机器学习方法却可以从许多硬信息、软信息和行为信息中获得，然后通过模型找出这些特征与违约结果之间深层的关联关系。从本文查阅的文献来看，对两种建模方法进行对比研究的文献很少，也没有给出将机器学习方法转化为信用评分卡模型的思路。因此，本文在通过分析国内外研究成果的基础上，将最新的机器学习算法XGBoost引入到信用风险建模领域，并对机器学习模型与传统评分卡模型进行了对比，且给出了机器学习模型转换为评分卡模型的思路。

二、背景技术

(一)信用评分卡理论

信用评分模型本质上是一种有监督学习模型，也是模式识别中的二分类问题。信用评分模型通常将客户群体分为非违约客户和违约客户，并根据历史上每个客户类别的若干样本，从历史已知数据中分析两类客户群体的特征，并根据分类规则建立数学模型，再利用模型计算贷款人违约风险作为消费信贷的决策依据。

一般来说，我们通常说的评分卡模型一般都是用于贷前审批，也称为贷前评分卡，用于贷前审批阶段对借款申请人的风险评估。逻辑回归模型是最常见的一种信用评分的模型，该模型理论基础比较完善，有很强的解释性，是目前商业银行信用评分卡开发的主要方法。逻辑回归是以贷款人违约与否作为因变量，一般称为“好样本”或者“坏样本”，用0或者1来表示。然后利用借款人已有的资料建立模型，对借款人违约的概率进行预测。模型表达式为：

(1)

通过式(1)得到的是客户违约概率估计，但在实际应用中通常需要转换为简单直观的评分，也就是要将概率值标准化为分数值。评分的校准是指通过线性转换将最终模型评分与好/坏比(odds)建立一定对应关系的过程。odds为好样本概率p与坏样本概率1-p的比值，其表达式为：

(2)

评分卡设定的分值刻度可以通过将分值表示为比率对数的现行表达式来定义如下：

score总=A+B×ln(odds)

(3)

设置比率为x(也就是odds)的特定点分值为P0，而PDO是指odds成为原来的两倍需要提高的分数。则比率为2x的点的分值为P0+PDO。带入式(3)可得到：

(4)

则：

(5)

由于P0和PDO的值都是已知常数，将计算出的A、B值带入式(3)，从而得到不同的x下的评分卡分值。

(二)XGBoost集成学习方法

XGBoost全名叫极度梯度提升(Extreme Gradient Boosting)，是基于树的boosting算法，最早由华盛顿大学陈天奇博士提出(2016)。其算法过程如下：

对于一个给定的数据集D={(xi，yi)}(|D|=n，xi∈Rm，yi∈R)，m是特征，n是样本容量。集成树模型的预测输出：

(6)

其中，F={f(x)=wq(x)}(q：Rm→T，w∈RT)是回归树空间，这里q表示每棵树的结构，它将一个示例映射到对应的叶索引。T是树的叶子数量，每个fk对应每棵树的结构q和叶子的权重w。不同于决策树，每一个回归树包含每个叶子的连续得分，用wi代表第i个叶子的得分。设目标函数为：

(7)

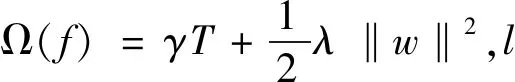
(8)

式(8)相对于式(7)增加了ft来改善模型，为了更快地优化目标函数，用二阶泰勒展开来近似原来的目标函数。

Lt≈

(9)

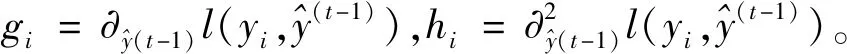
在不考虑常数项的情况下，简化后的目标函数为：

(10)

定义Ij={i|q(xi)=j}

则：

(11)

对于给定q(x)可以计算出叶子j的最优权重wj：

(12)

计算相应的最优目标函数值：

(13)

式(13)可以用来计算树的结构q的得分，但通常情况下不可能列举出所有可能的树的结构q，利用贪心算法每一次尝试对已有的叶子加入一个分割，假设IL和IR是左右子树分数分割后的节点，令I=IL∪IR，分割后的损失函数如式(14)：

Lsplit=

(14)

为了防止过拟合，XGBoost也采用了Shrinkage方法来降低过拟合的风险，Shrinkage技术最早由Friedman(1999)提出。除了利用Shrinkage技术来抑制过拟合外，XGBoost在构造树模型过程中也借用了随机森林中随机选择一定量的特征子集来确定最优分裂点的做法，以达到抑制过拟合的目的。特征子集越大则每个弱分类器的偏差就越小，但方差就越大，子集的比例可以通过利用交叉验证来确定。

(三)模型评价指标

对信用评分模型来说，在建立模型之前最重要的一步是进行变量选择，变量选择通常会根据变量的IV值大小来确定变量是否可以进入模型。IV的全称是Information Value，中文意思是信息价值，或者信息量，可以用来衡量自变量的预测能力，类似的指标还有信息增益、基尼系数等。如果要计算IV值，首先需要计算WOE，WOE的全称是Weight of Evidence，即证据权重。WOE是对原始自变量的一种编码形式。WOE、IV的计算公式为：

IVi=(pyi-pni)×WOEi

其中，pyi是这个组中坏样本占所有样本中所有坏样本的比例，pni是这个组中好样本占样本中所有好样本的比例，yi是这个组中坏样本的数量，ni是这个组中好样本的数量，yT是样本中所有好样本的数量，nT是样本中所有坏样本的数量。

一般来说，机器学习方法分类模型有些重要的评价指标，如混淆矩阵、ROC、AUC、KS值等。其中，混淆矩阵的表达式见表1。

表1 混淆矩阵

根据表1混淆矩阵的结果可以计算出相应的机器学习模型的评价指标，常用的评价指标有以下几种，见表2。

表2 机器学习常用评价指标

以FPR为横坐标，TPR为纵坐标，把不同的点连成曲线，得到ROC曲线。ROC、KS曲线原理见图1、图2所示。

ROC曲线被称为受试者工作特征曲线(receiver operating characteristic curve)，又称为感受性曲线(sensitivity curve)。从图1可以看出ROC曲线是以假阳性概率(false positive rate)为横轴，真阳性概率(true positive Rate)为纵轴所组成的坐标图。ROC曲线下方与坐标轴围成的面积叫做AUC(Area Under ROC Curve)，AUC值越大说明分类器性能越好。

图1 ROC曲线图

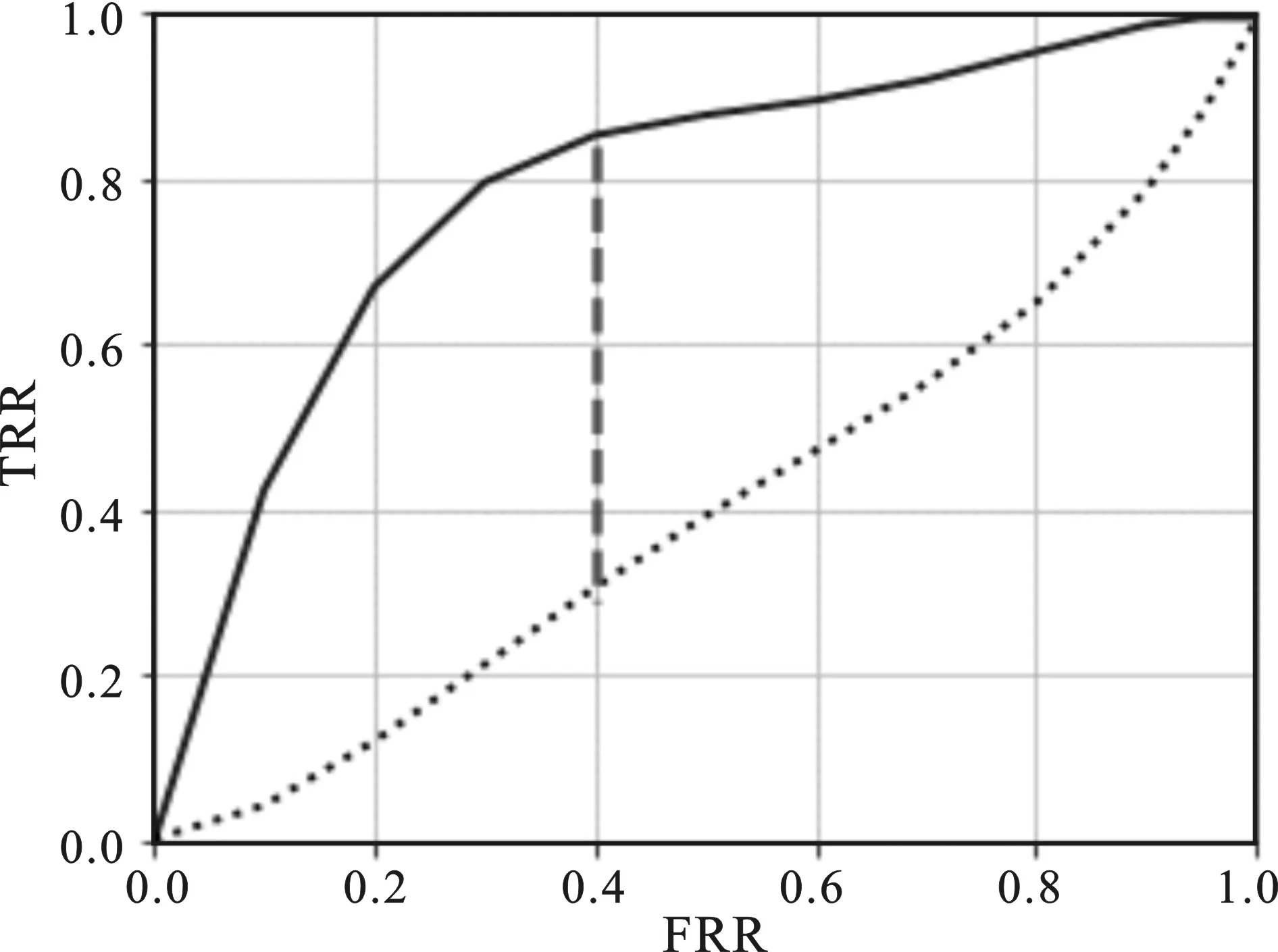
图2 KS曲线图

KS曲线也叫做洛伦兹曲线(Kolmogorov-Smirnov curve)，KS值是对模型风险区分能力进行评估的最重要指标，该指标衡量的是好坏样本累计分布之间的差值，好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。另外，从图2可知，KS曲线和ROC曲线的画法类似，在不同的概率阈值下，计算出不同的FPR和TPR值，再分画出TPR和FPR曲线，则两条曲线之间的距离就是KS值。不同的KS值对应的模型评价标准见表3。

表3 KS值评价标准

模型上线后，还需要对实际运行情况进行监测，模型运行稳定性的评价指标为PSI(Population Stability Index)，也叫做群体稳定指数，是最常用的模型稳定性评价指标，计算公式为：

PSI=∑(Actual%-Expected%)×

其中，预期占比Expected%和实际占比Actual%分别表示在模型训练样本和测试样本中，对应分数段或违约率段内的人群占比。一般地，PSI小于0.1代表模型稳定性高，即模型运行情况与模型训练时的表现基本相同；大于0.1且小于0.25代表模型稳定性中等；大于0.25代表模型稳定性较差。

(四)模型理论对比分析

建立个人信用评分模型时既需要对信用风险管理理论及信用评分建模方法进行规范研究，也需要探讨建立评分模型的理论基础。常见的信用风险模型主要有专家评分模型、统计评分模型和机器学习模型。

专家评分模型是一种传统的信用风险评估方法，在数据积累不够的条件下，由于缺少借款人较为全面和系统的历史资料数据，金融机构对借款人信用状况的评估只能依靠信贷专家根据其主观经验进行判断，形成专家评分模型。专家评分方法有很高的灵活性，处理定性指标具有非常突出的优势，但由于其过分依靠信贷专家的个人经验，主观随意性较强，评估结果之间可能会有较大差距，但预测精度效果一般。

统计评分卡模型是目前金融机构信用评估领域应用最为广泛的模型，一般采用Logistic回归模型。该方法无需假定特征变量的概率分布，也不要求等协方差性，其最大的特点是模型的可解释性强，模型稳健性较好。但信用评分卡模型只能选取少数变量，使得其无法直接应用于大数据环境下的个人信用风险管理，从而预测精度有限。

机器学习模型无需在严格的假设条件下进行建模，而且对数据分布无任何要求，且预测精度高。但该方法可解释性差，存在算法的“黑箱”问题，而且在面对信用数据的变化时显得不够稳健。由于风控人员很难掌握机器学习模型内部的逻辑依据，目前传统的金融机构仅仅在尝试这些新的机器学习评估方法，要全面推广还有很长的路要走。

三、实证分析

实验数据来自于国内某P2P网络借贷公司2017年4至8月实际交易40 678笔贷款数据，借款人借款周期为一个月。滚动率根据历史数据计算M0(未逾期)递延至M1(逾期1～29天)，M1递延至M2(逾期30～59天)，以此类推。根据滚动率模型，发现逾期客户进入M2后还款比例已经很低，故“坏客户”采用逾期进入M2的客群。

本文在实验中将40 678个贷款样本中32 537个正常还款样本标记为0(无逾期)，8 141个逾期样本标记为1(逾期超过30天)，odds为3.99。样本信息维度包括银行卡交易信息、多头借贷信息、个人基本信息、运营商信息、电商交易信息、信用卡支付信息、社交软件群关键词命中信息、四要素匹配度、短信高风险9个维度547个变量名称，所有变量IV值都超过了0.01的基本阈值条件。

(一)信用评分卡模型

信用评分卡模型需要进行变量筛选，一般只需选择10～12个变量用于评分卡模型建立。变量筛选过程采用IV值，并结合WOE趋势和业务逻辑，选择IV值大于0.05且WOE趋势单调的变量，同时去掉相关系数过高的变量。其中，信用卡交易信息变量选择过程如表4所示。

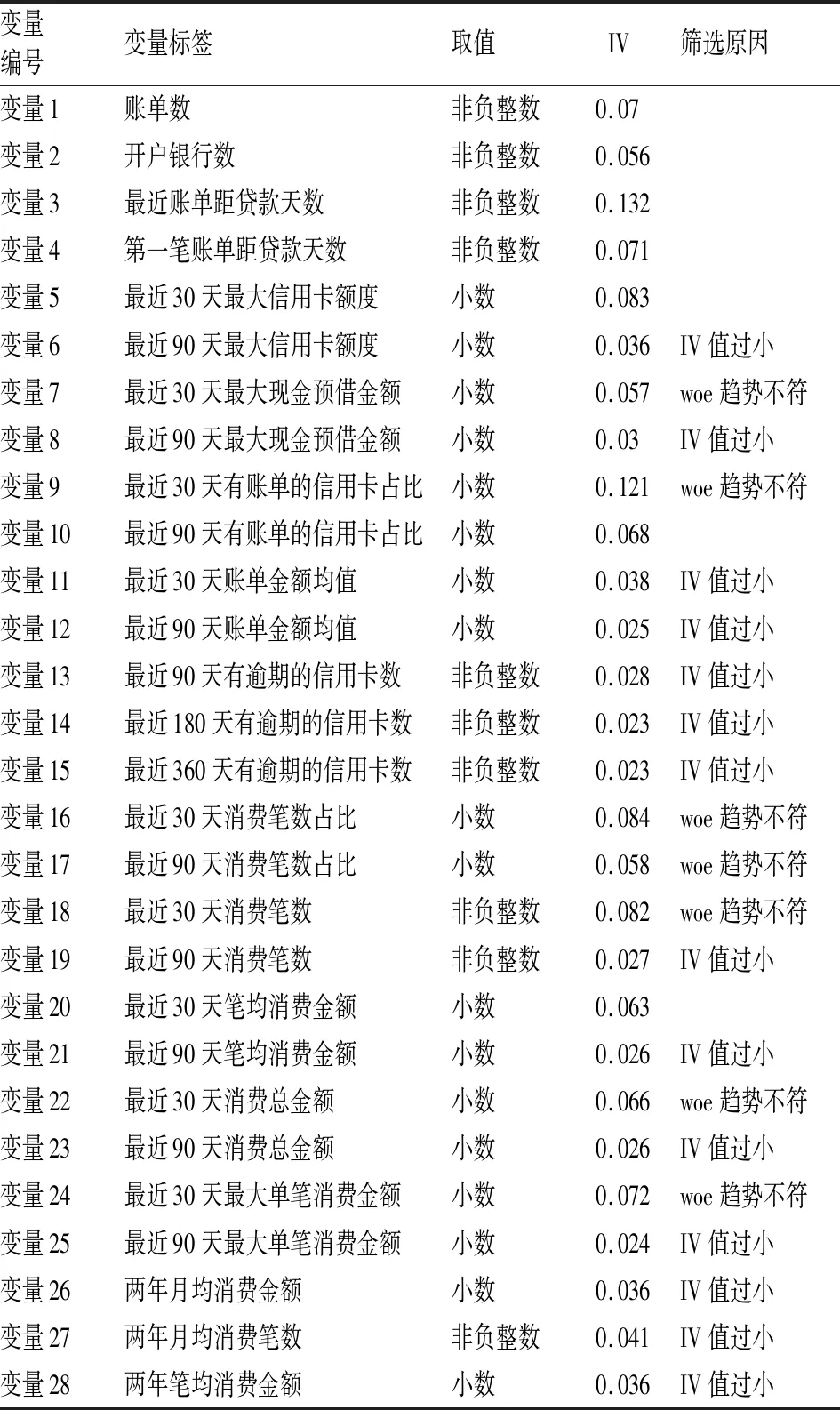
表4 信用卡交易信息变量选择示例

注：数据来源于某互联网P2P网络借贷公司。

从表4可以看出，根据IV值、WOE趋势、相关系数和变量的业务逻辑原则，从信用卡交易信息维度28个变量中选出了7个变量。按照与此相同的方法，从个人基本信息、运营商信息等变量维度挑选出的所有变量见表5。

表5 最终入模变量

将表5中最终选出的16个变量放入逻辑回归模型，并采用逐步回归的方式，通过逻辑回归方法，模型最终选出的信用评分卡变量见表6。

利用逻辑回归中的逐步回归法，模型从16个变量中选出了11个变量作为信用评分卡所采用的最终变量。利用SAS软件编程，最终得到的评分卡模型见表6。

利用表6的评分卡模型对测试集样本进行评分转换，得测试集样本的最终得分情况见表7。

从表7的评分卡得分情况可以看出，随着用户得分的上升，高分段的坏账率呈现出不断下降的趋势，这也说明了评分卡模型可以较好地识别信用风险。评分卡模型效果评估结果见表8。

从表8看出，模型的KS值测试集为0.346 5，说明评分卡模型有一定的效果。

(二)XGBoost机器学习模型

相对于传统评分卡模型，机器学习模型过程更为简洁，无需进行变量筛选，将所有547个变量输入模型，预测测试集样本信用违约概率。试验采用XGBoost算法，通过参数寻找最优方法，学习率设为0.01，树深度为5。另外，本次实验考虑了对样本缺失情况进行补缺的分析，并采用中位数补缺的方法进行缺失值填补。在包含缺失值和不包含缺失值的情况下，XGBoost算法模型的预测结果对比见表9。

从表9可以看出，包含缺失值的XGBoost模型效果要好于利用中位数补缺后的模型，这也说明在对模型进行缺失值补足后可能会带来更多的数据噪音，从而影响实验结果，因此本研究采用不对缺失值进行处理的方法。在不考虑缺失值的情况下，XGBoost模型KS值的计算结果见图3所示。

表6 最终评分卡模型

表7 测试集样本得分情况统计

表8 模型结果评估

表9 包含缺失值的模型预测结果

从图3中可以看出，KS值可以通过累计坏样本与累计好样本之差来实现，在本次实验中，模型在预设概率为0.6的条件下实现的最大KS值为0.471 5。

图3 KS值计算结果图

由于企业在实际生产经营环节中，模型的运用需要考虑公司实际经营情况。一般来说，贷款机构特别关注模型将坏客户预测为好客户的情况，而为了减少这样的情况出现，机构可以通过提高贷款评分，也就是只贷款给那些信用得分较高的客户的方法来实现。但这样操作的结果必然会出现大量申请人被拒绝的情况，也就是对应的进件通过数量的下降，这无疑会降低公司的营业额。根据这种情况，本次试验列出了在不同的预设概率下，XGBoost模型预测结果，其指标统计见表10。

表10 不同预设概率下的实验结果统计

从表10可以看出，模型在预设概率为0.6～0.65的条件下(也就是当且当某个进件客户预测为好人的概率大于0.60才表示通过筛选)，实现了最高的KS值为0.471 5，且有60.30%的申请客户通过了借款申请，但模型也将7.5%的坏样本误判为好样本。如果从实际业务的角度出发，贷款机构可以通过综合比较三个指标的情况，选择一种最适合公司经营情况的预设概率阈值。另外，通过比较表7和表10也可以看出，机器学习模型的预测结果在预设概率为0.6的条件下效果要远好于信用评分卡模型0.35的KS值，这也说明了机器学习方法的预测能力的确要优于传统的信用评分卡模型。

另外，为了使得机器学习模型的输出结果更具有可操作性，也可将机器学习模型输出概率值转换为常见的信用评分值。在假设基础分为500，指定比率2倍的分数(PDO)设为10，P0设为50的情况下，表10的结果转换为传统信用评分的情况见表11。

表11 机器学习模型转换为信用评分

从表11可以看出，机器学习模型也可以通过信用评分卡转换法转换为常见的信用评分，说明机器学习方法除了预测能力更好之外，还可以与传统方法相互融合，从而构建更加有效的风控体系。

四、结 论

本文根据中国在线信贷业务行业的特点，尝试建立了一套从多个数据维度评估个人信用风险的新模式，数据维度包括贷款申请者的基本信息、银行卡信息、电商数据、多头借贷信息、社交网络信息等，共选择了547个变量，拓展了在线信贷业务变量选择的维度空间，也拓宽了个人信用风险的风控模型设计框架。建立了基于机器学习算法的大数据风控体系，同时将其与传统的信用评分卡模型进行比较分析，得出了以下主要结论：

1.数据质量直接影响模型效果。从本文的研究结果来看，不同的算法模型可以获得不同的预测效果，但算法只能逼近模型最优效果，如果要继续提高模型的预测精度，那就需要不断地接入更多的数据维度，并进行变量特征选择。对于金融机构的风控从业人员来说，分析研究客户日常行为数据，并从大量数据中提取有效特征将成为日常主要工作。

2.传统评分卡模型具有一定的局限性。评分卡模型虽然具有较强的可解释性，但建模过程复杂，本文在实证部分中，通过利用IV值、WOE和相关性分析等方法，挑选出部分变量。在此基础上，通过逻辑回归中的逐步回归法，最终选择11个变量建立了评分卡模型，最后还需要将评分卡的输出值转化成标准的信用评分。在建模过程中，必然会造成大量信息的损失，因此模型预测效果会受到一定的影响。

3.利用机器学习方法可以建立有效的大数据风控体系。本文利用最新的XGBoost算法，并使用了全部547个输入变量进行试验预测，模型KS值最高达到0.47，超越了传统评分卡模型0.35的KS值，也可以将机器学习方法输出的预测概率值转化为传统的评分模式，使机器学习方法具有更好的可解释性和可操作性。与传统的评分卡模型相比，基于机器学习方法设计的风控模型无需建立在严格统计假设条件下，且预测效果更加准确，这使得机器学习方法可以比传统的评分卡模型表现更为出色。当然，本文并非否定了逻辑回归方法在信用评分中的有效性，反而认为逻辑回归的强可解释性是机器学习方法“黑箱”问题无法逾越的鸿沟，如何将机器学习方法与传统逻辑回归方法进行有机结合将是本文后期的研究重点。