多星博弈拦截Nash和Pareto策略研究*
2019-09-19徐东宇王淳宝
徐东宇 王淳宝 赵 硕 叶 东
1.哈尔滨工业大学航天学院,哈尔滨150001 2.中国空间技术研究院,北京100094 3.航天东方红卫星有限公司,北京100094
随着科技的发展,未来战场态势必将越来越复杂,而卫星作为空间力量的重要组成部分,在提供战场信息时具有传送信息量大、不受地形限制等优点[1],为了夺取空间信息主动权,对敌方卫星实施拦截打击有着重要意义。
针对拦截问题,文献[2]基于滑模面进行了导弹的制导与控制一体化设计,仿真表明了采用所设计的控制方法能够满足拦截要求。冯[3]分析了视线角和视线角速度对动能拦截器末制导的影响,通过划分参数域,给出了拦截域和突防域的分布,分析了参数对其影响。赖[4]考虑目标进行程序机动时的拦截策略,基于动态面和扩张状态观测器对制导与控制进行了设计,仿真分析了目标在进行正弦机动时,采用相应的控制策略能够实现对目标的精确拦截。李[5]分别研究了拦截卫星的中制导和末制导方法,基于Lambert轨道转移设计了中制导策略以接近卫星,完成交班后进入末制导过程,采用滑模控制策略实现精确拦截。虽然上述文献对目标拦截问题均进行了研究,但并未考虑目标的机动性,且仅考虑单个拦截器。而随着科技的发展,目标可以进行自主决策,采取相应的策略以应对不同的战场态势,此时拦截策略的设计需要考虑目标的最优机动性,传统的单边拦截策略已不再适用,此时为了实现可靠拦截,通常需要多颗拦截器,因此研究多拦截器的合作拦截策略有着重要的意义。
针对博弈拦截问题,学者们已经进行了充分的研究。文献[6]中作者以小车模拟导弹拦截态势,基于深度确定性策略梯度算法设计了追逃策略,该方法能够实现对目标的有效拦截,具有较强的自适应性。Horie[7]等基于飞机三维动力学模型,通过微分对策理论将优化拦截问题转化为两点边值问题,通过仿真得出,最优飞行轨迹分为偏离垂直平面以及垂直面内运动2个阶段。当拦截器距离目标较近时,拦截过程进入末端拦截,针对航天器末端拦截问题,Prussing[8-9]等应用主矢量理论分别研究了多脉冲逃逸策略以及拦截策略。文献[10]考虑航天器拦截目标后返回原轨道的情况,通过在目标函数中引入一个参数k对路径进行约束。Gutman S[11]在双积分动力学模型的基础上,以终端相对距离为指标建立了拦截器与目标的控制策略,分别给出了在极坐标、球坐标下的策略形式。文献[12-13]在给出拦截器与目标控制策略的基础上,建立了关于拦截剩余时间的一元四次方程,以求解终端拦截时间,并讨论了方程的分叉现象。文献[14]考虑拦截过程中视线角测量存在噪声的情况,通过状态观测器对其进行估计,再将其应用于控制策略。对于多星合作博弈问题,LIU[15]考虑2枚导弹拦截同一目标,在简化的导弹动力学模型基础上,通过Nash均衡集设计最优加速度方向,即最优制导率。文献[16-17]中均以平面双积分系统为模型,通过可达集设计合作拦截时的最优策略。文献[18]中假设拦截器与目标速度不变,基于阿波罗尼圆设计初始速度方向角以实现最优拦截。
对于航天器末端拦截问题,虽然已经存在较多的研究,但大多局限于双星博弈或简化模型的多星博弈,与实际情况相差较大。针对多星博弈拦截问题进行研究,分别推导了各拦截器非合作的Nash反馈策略,以及合作的Pareto反馈策略。
文章安排如下:1)建立末端拦截动力学模型;2)以终端零控脱靶量为指标推导了各拦截器非合作态势的Nash均衡解;3)推导了各拦截器以合作方式态势进行拦截的Pareto均衡解;4)将博弈策略应用于多星博弈拦截,并进行了仿真分析。
1 末端拦截动力学模型
末端拦截过程中,拦截器与目标距离较近,因此在拦截器附近建立参考卫星,如图1,其中O为地心;O1为参考卫星;P为拦截器。设参考卫星运行在圆轨道,则在轨道坐标系下,拦截器相对参考卫星的动力学方程可简化为CW方程
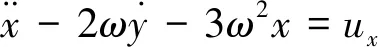
(1)
式中:x,y和z为拦截器相对参考卫星的位置;ω为参考卫星的轨道角速度;ux,uy,uz分别为拦截器的控制输入。
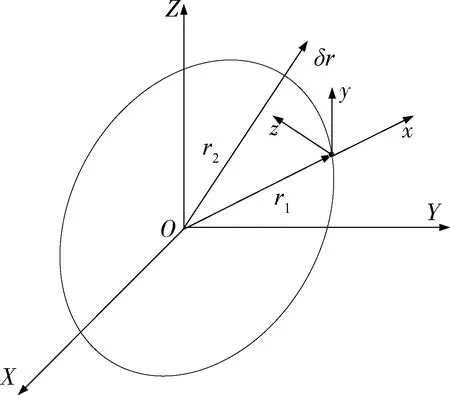
图1 拦截器与参考卫星

(2)

由线性系统理论可得状态转移矩阵为
(3)
其中,子矩阵分别为[19]


设末端拦截段存在N个拦截器P1,…,PN与目标,其动力学均满足CW方程,即

(4)

分别定义拦截器P1,…,PN与目标的相对状态
XPiE=XPi-XEi=1,…,N
对其求导并将式(4)代入,可得相对状态方程

(5)
在多星拦截过程中,拦截器与目标围绕拦截终端距离展开争夺,因此仅需考虑星间的位置矢量[20]。分别定义拦截器P1, …, 拦截器PN与目标的零控脱靶量,对系统进行降维
ZPiE(t)=DΦ(tfi,t)XPiE其中,i=1,…,N
(6)

对式(6)求导,并结合可得

(7)
式中:BPi=DΦ(tfi,t)B=Φ12(tfi,t);CEi=-DΦ(tfi,t)C=-Φ12(tfi,t)。
对于多星博弈问题,根据各航天器是否合作拦截,将其分为Nash均衡策略和Pareto均衡策略。
2Nash博弈策略设计


(8)

对于航天器拦截问题,要求在有限时间内使目标进入某一拦截器的拦截范围,因此各拦截器的指标函数定义为其与目标的终端零控脱靶量范数。
根据Nash均衡定义,分别定义拦截器Pi(i=1,…,N)和目标的指标函数如下
(9)
(10)

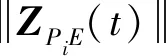

(11)

(12)
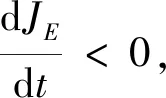

(13)
其中:ki(i=1,…,N)代表了目标对各拦截器的博弈程度:
若ki>kj(j={1,…,N}i), 则目标主要与拦截器Pi进行博弈,即主要躲避Pi;
若ki
若ki=kj(j={1,…,N}i), 则目标进行无差博弈,即同等程度躲避拦截器Pi和Pj。
3Pareto博弈策略设计
通过Nash反馈策略,各航天器虽然可以达到均衡态,但由于并非合作关系,拦截系统可能并未达到最优状态,因此对于多星博弈问题,设各拦截器采取合作策略,使系统达到Pareto均衡。


(14)

对于Pareto均衡,拦截器的优化指标为式(9)的凸组合,即
(15)
(16)
其中,ki(i=1,…,N)定义与第2节相同

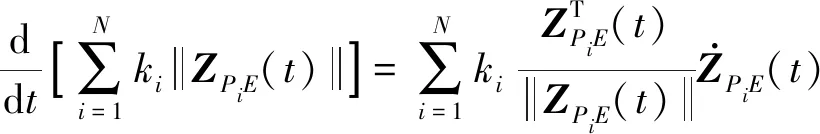
(17)


(18)
类似地,目标的控制策略UE仍为

(19)
通过比较Nash反馈策略式(12-13)和Pareto反馈策略式(18-19)可知,拦截器无论采取合作或非合作拦截方式,其博弈策略均相同,即各拦截器采取非合作方式,即可达到合作拦截的目的。
4 仿真结果及分析
由于合作与非合作策略相同,因此只对合作态势下的多星博弈拦截问题进行仿真。
考虑2颗拦截器进行仿真,初始条件如下:假设拦截器P1和P2及目标均在地球同步轨道附近运动,则将参考卫星选为GEO轨道上与其相近的卫星,轨道角速度为ω=7.2722×10-5rad/s。拦截器P1初始位置为[-2;0;1]km,初始速度为[0;-0.005;0.005]km/s;拦截器P2的初始位置为[1;1;0]km,初始速度为[0.01;0;0.005]km/s;目标的初始位置为[0;0;0]km,初始速度为[0;0.005;0]km/s。设拦截器P1的推力幅值为ρP1=0.686m/s2,拦截器P2的推力幅值为ρP2=3/2ρP1m/s2,目标的推力幅值为ρE=1/2ρP1m/s2。此外,设拦截器的拦截半径l=0.01km。
1) 合作博弈态势。设终端拦截时间tf=100s,且目标的综合权重为k1=0.5,k2=0.5。
图 2给出了各航天器的运动轨迹,图3绘制了博弈过程中各拦截器与目标之间相对距离的变化情况。可以看出,在100s时,拦截器P1和P2与目标的相对距离均达到了0,满足拦截要求,即实现了对目标的拦截。

图2 多星博弈的三维运动轨迹

图3 多星博弈的相对距离变化
2)目标综合权重对拦截的影响。设终端拦截时间tf=100s,目标综合权重为k1=0.8,k2=0.2,此时目标主要躲避拦截器P1。
图4和5分别给出了三星的运动轨迹,以及相对距离的变化情况。可以看出,由于目标主要对推力幅值较大的拦截器P1进行躲避,导致在100s的终端时间条件下,拦截任务失败,此时只能通过延长拦截时间实现对目标的拦截。

图4 多星博弈的三维运动轨迹

图5 多星博弈的相对距离变化
5 结论
针对多星博弈末端拦截问题,分别考虑了多拦截器非合作与合作态势下的拦截策略,基于Nash均衡建立了非合作博弈策略,基于Pareto均衡建立了合作博弈策略。通过比较,2种态势下各拦截器策略相同。最后,仿真验证了采用提出的博弈策略,拦截器可以实现对目标的拦截,且不同的综合权重将导致不同的拦截结果。
