基于变步长LMS算法的交流阻抗测钢筋腐蚀

(青岛理工大学 信息与控制工程学院，山东 青岛 266000)

钢筋混凝土在楼宇、桥梁等建筑中有着极其重要的作用，钢筋锈蚀是导致混凝土结构劣化的最主要因素[1-2]。钢筋腐蚀会严重破坏混凝土结构的耐久性，钢筋腐蚀问题必须引起足够的重视。在多种钢筋腐蚀测量方法中，交流阻抗法精度较高，影响因素小，可以实现无损检测，所以应用比较广泛。史美伦[3]等人提出用两个不同的阻抗函数来描述钢筋腐蚀的相关信息；伍远辉[4]等人用交流阻抗谱研究了混凝土钢筋浸泡在氯离子溶液中的阻抗谱特征，测量结果仍然存在一定误差。

交流阻抗法在测量钢筋腐蚀程度时存在缺点，其响应信号属于微弱信号，在进行腐蚀参数分析时信噪比较低，得到的钢筋腐蚀的结果并不准确。最小均方(LMS)算法具有计算难度小、鲁棒性好等优点，所以应用比较广泛[5-8]，但是其收敛速度和稳态误差无法达到一个很好的平衡，两者无法同时获得较好的效果。LMS中，步长因子的大小在收敛过程中起着十分重要的作用[9]。文献[10]建立了一种步长因子与瞬时误差的函数关系，但是该算法中步长因子的迭代会引入噪声导致系统存在稳态误差。文献[11]提出了一种基于S函数的变步长自适应滤波算法，其中步长因子与误差之间的函数关系为S函数，该算法在加快收敛速度的同时一定程度上减小了稳态误差，但最终伴随算法的运行，步长因子改变频率越来越快，使系统仍然存在稳态失调的可能性，滤波效果还有待进一步完善。考虑到这些不足，结合交流阻抗法中交流阻抗谱的腐蚀参数测量原理，提出一种基于变步长LMS自适应滤波算法应用于交流阻抗法测量钢筋腐蚀，该算法在步长因子和误差之间建立了一种新型的非线性关系，在提高收敛速度的同时能够满足系统稳态性能的要求。与常规交流阻抗法相比，在保证施加信号为小幅度交流信号的前提下，仿真证明改进的算法具有传统算法所不具有的高精度和高信噪比，通过与几种常用滤波算法的实验数据进行比较，发现此算法有更高的稳定性和准确性，能起到较好的滤波效果。

1 交流阻抗法原理

作为电化学测试技术的一种研究方法，交流阻抗法施加小幅度交流信号扰动于研究对象，在稳态时观察体系对扰动的跟随情况[12]。交流阻抗法测量钢筋腐蚀的简单构造如图1所示，对钢筋混凝土系统施加交流信号，利用探针获取响应信号，使用探针可以提高测量的信噪比，而且测量方式比较简单。

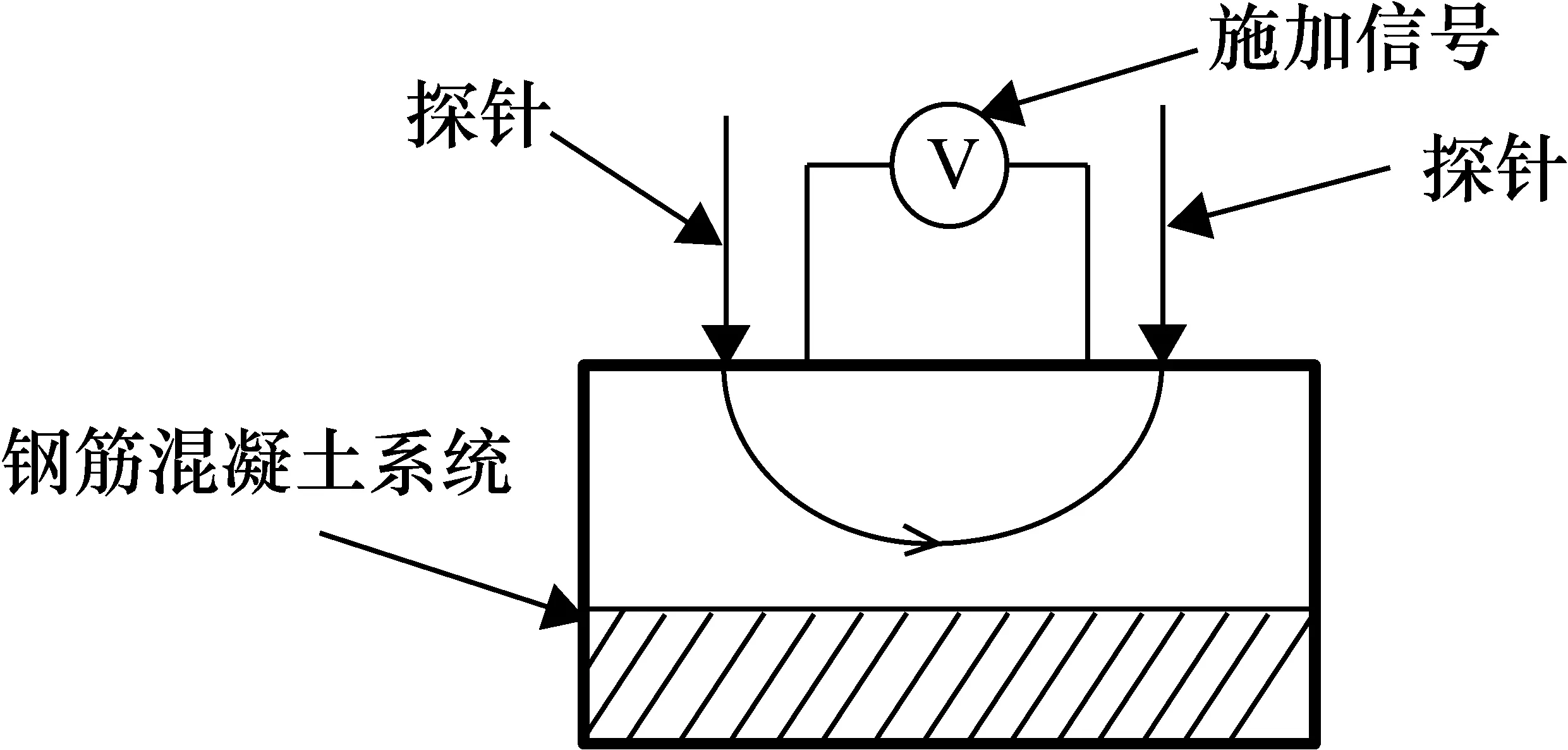
图1 交流阻抗法测量钢筋腐蚀的简单构造图

对钢筋混凝土系统施加电压信号

U(ω)=U0sin(ωt)

(1)

式中，U0为小幅施加电压交流信号幅值；ω为角频率，ω=2πf。

施加信号经过钢筋混凝土系统后会有一个响应信号，利用探针获取的响应信号为

I(ω)=I0sin(ωt+θ)

(2)

式中，I0为响应交流电流信号幅值；θ为响应信号与施加信号之间的相位角，响应信号与施加信号同频率。概括来说，就是对钢筋混凝土系统施加不同频率的小幅度交流信号，测量响应信号，以此得到交流阻抗谱，在不同频率的情况下对钢筋混凝土系统进行交流阻抗测量，可以得到复数阻抗随频率变化的曲线，即交流阻抗谱[13]，通过阻抗谱能够得到腐蚀参数，进而对腐蚀情况判定。等效电路如图2所示。

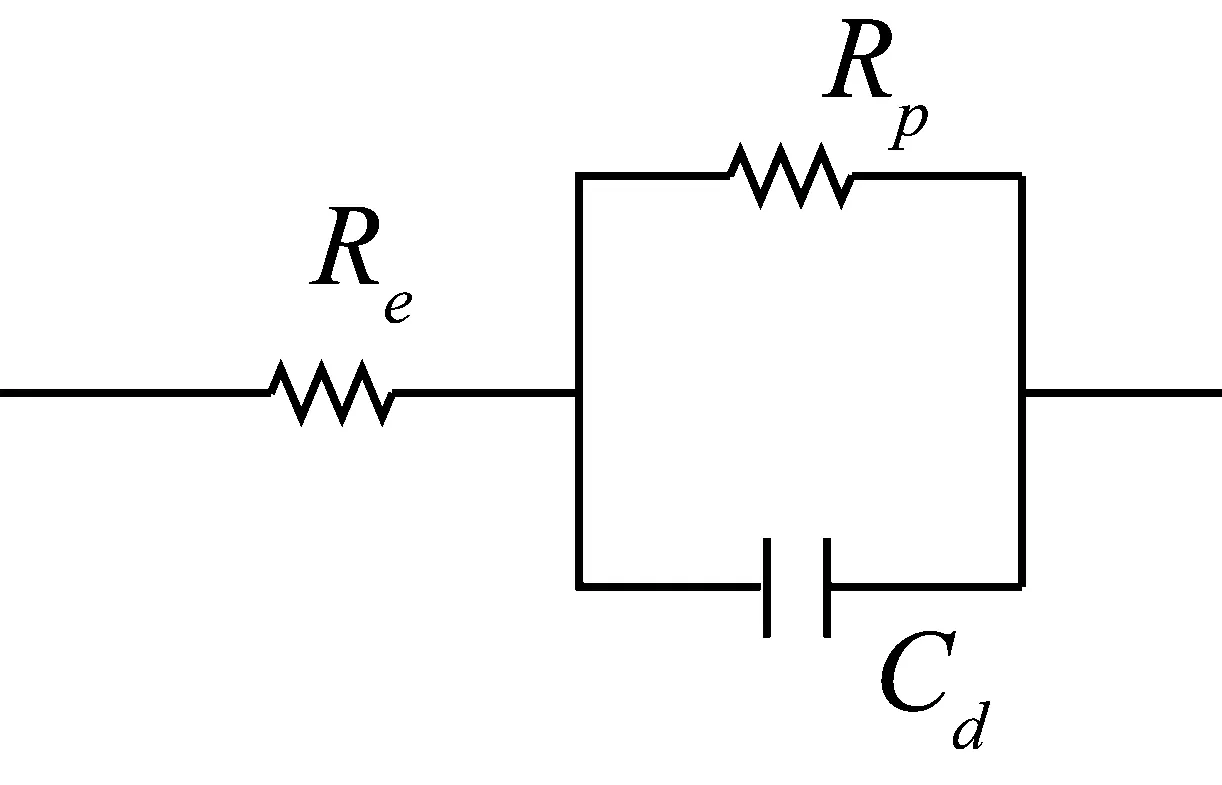
图2 交流阻抗法测量钢筋腐蚀的简单构造图

其中Re为电极电阻，Rp为极化电阻，Cd为界面电容特性，复阻抗为

Z=Zr+jZi

(3)

根据式(3)可得

(4)

相位角的正切值为

(5)

将式(5)代入式(4)消去角频率ω可得

(6)

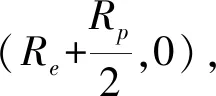
当采用交流阻抗法测量获得钢筋腐蚀参数时，由于施加信号是毫伏级的微弱信号，所以容易受到噪声等信号的干扰，所以需要一种可靠的方式去除干扰信号，采取一种改进的自适应滤波算法来去除干扰信号，会使测量结果更加准确。

2 传统自适应滤波器原理性能分析

2.1 自适应滤波器结构

典型的自适应滤波器的结构图如图3所示。其中x(n)为输入信号，y(n)为输出信号，d(n)期望信号，e(n)为误差，其计算公式为

e(n)=d(n)-y(n)=d(n)-WT(n)X(n)

(7)

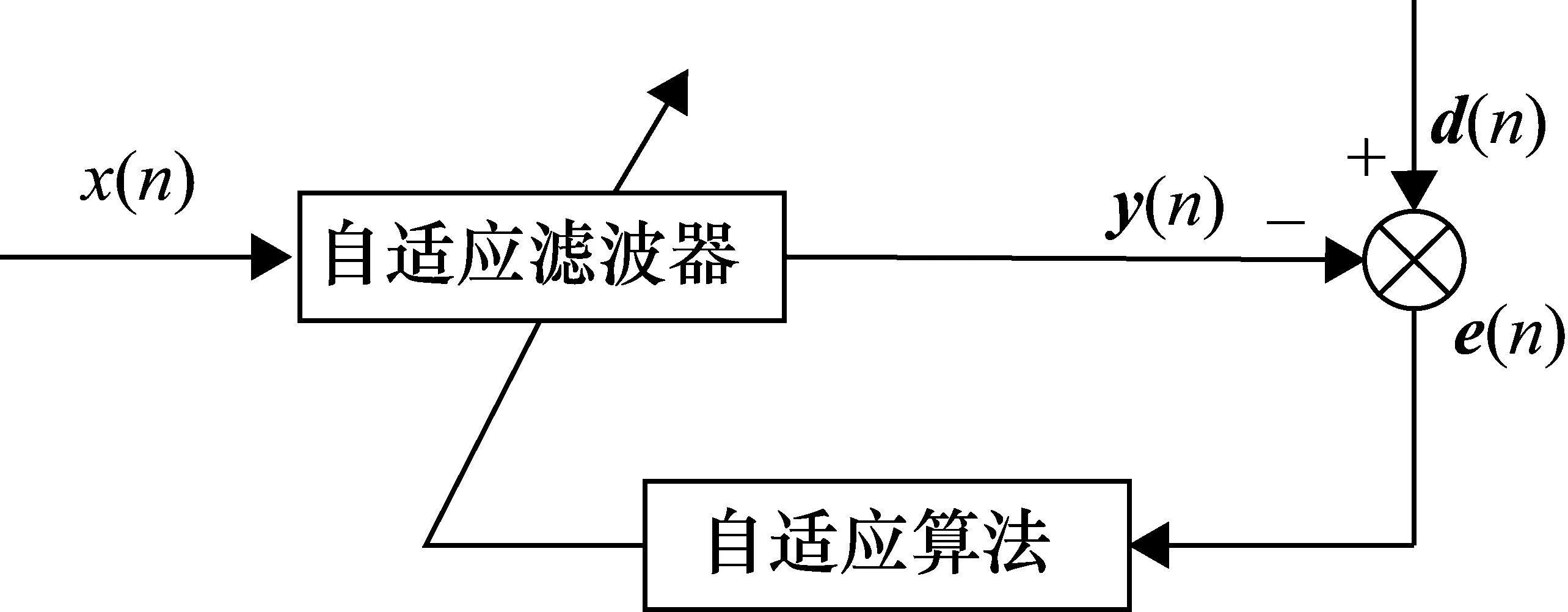
图3 自适应滤波器结构框图

2.2 传统LMS算法原理及分析

自适应滤波算法有最小均方误差(LMS)算法、最小二乘(LS)算法、最大信噪比算法、统计检测算法等，其中LMS算法是Widrow和Hopf在1959年研究自适应线性元素的模式识别方案时提出的[14]。LMS算法由于其具有结构简单、计算量小、收敛性和稳定性较好等优点而得到广泛应用。

使用LMS算法，目的是得到最小的滤波器的均方误差，这样可以不断更新滤波器系数，使期望信号与滤波器输出信号之间的误差e(n)无限缩小，即在某种程度上，滤波器的输出信号和想要得到的期望信号实现了匹配[15]。均方误差可表示为

J(n)=E{e2(n)}=E{[d(n)-y(n)]2}

=E{d2(n)-2d(n)y(n)+y2(n)}

=E{d2(n)}-2E{d(n)WT(n)X(n)}+

E{WT(n)X(n)XT(n)W(n)}

=E{d2(n)}-2PWT(n)+WT(n)RW(N)

(8)

式中，R为输入信号x(n)的自相关矩阵；P为输入信号x(n)与期望信号d(n)的互相关矩阵，其表达式分别为

R=E{X(n)XT(n)}

(9)

P=E{X(n)d(n)}

(10)

自适应滤波器的设计准则是滤波器输出y(n)与期望信号d(n)之间的均方误差J(n)为最小值，要想得到最小的均方误差，需要满足式(11)，即

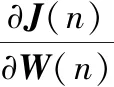
(11)

解得，

W(n)=R-1P

(12)

根据最速下降算法，沿着性能曲面负梯度(最速下降)方向调整滤波器权系数W(n),可以最快达到收敛的目标值，权向量的迭代公式为

W(n+1)=W(n)+u[-▽J(n)]

(13)

式中，u为步长因子。

在LMS算法中，用瞬时误差的平方代替均方误差，则可以对滤波器瞬时抽头的权向量求梯度，其表达式为

=-2e(n)X(n)

(14)

将式(14)代入式(13)可得

W(n+1)=W(n)+2ue(n)X(n)

(15)

从以上推导公式可以看出，传统的LMS算法因为其计算简单、易于实现、鲁棒性好等优点而被广泛使用，但是其收敛速度和稳态误差无法达到一个很好的平衡，存在步长取值固定,无法兼顾收敛速度和稳态误差等不足[16]。从式(15)可以看出，通过增大步长因子u可以提高收敛速度来消除较大误差，得到一个无法消除的较小误差[17]，当误差较小时，步长因子太大会使系统的稳态误差变大，甚至使系统处于失调状态，所以传统的LMS算法因为其固定的步长因子而不具有对时变系统的跟踪能力。

3 改进的变步长LMS算法

3.1 变步长LMS自适应滤波算法原理

为了改善自适应滤波算法,文献[9]完善了传统的自适应滤波算法，实现了改变步长的滤波算法(SVSLMS)，上文算法的改进在一定程度上完善了传统滤波算法的不足。在某些系数发生未知改变或处于实验初步摸索阶段时，步长因子变大的同时收敛速度变快，跟踪速度有明显增快的趋势，但当算法处于收敛阶段时，要想实现较小的稳态误差，步长因子应尽量小，才能避免出现稳态失常现象。本系统实现了基于S形生长曲线函数的变步长算法(SVSLMS),其中，u(n)为e(n)的S形生长曲线函数。

u(n)=f(e(n))

=β(1/(1+exp(-α|e(n)|))-0.5)

(16)

其中常数β控制S函数的范围，常数α控制S函数的形状。本算法实现了收敛速度尽量快、稳态误差尽量小的要求，完善了传统的自适应滤波算法。但是，本算法e(n)在原点处波动较大，因而本算法仍存在不足之处。

3.2 新的变步长LMS算法

文献[18]在文献[11]的基础上，针对其存在的不足，对步长因子u(n)和误差e(n)之间的函数关系进行改进，建立了一种新的非线性关系，如式(19)所示，使计算量较小并提高了收敛性，取得了较好的滤波效果。改进后的新算法中步长因子u(n)和误差e(n)的曲线图与文献[8]所提出算法的对比效果如图4所示。从图中可以看出，经过改进的算法效果有了明显的改善，使得步长因子在误差e(n)接近零处变化平缓，减小了系统的稳态误差，很大程度上避免使系统处于稳态失调状态。

u(n)=β(1-exp(-α|e(n)|2))

(17)

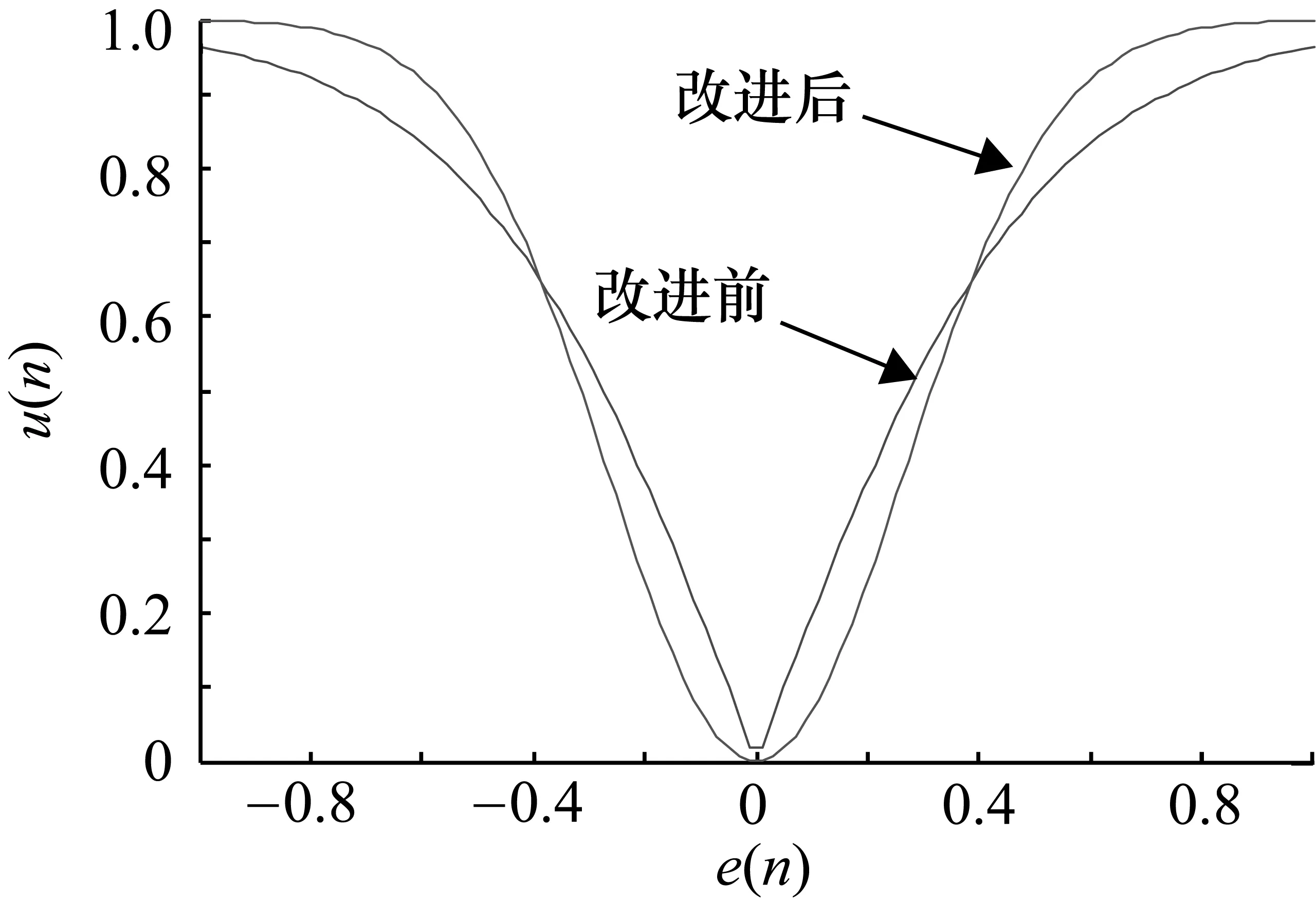
图4 改进后与改进前的u(n)与e(n)的关系曲线对比图

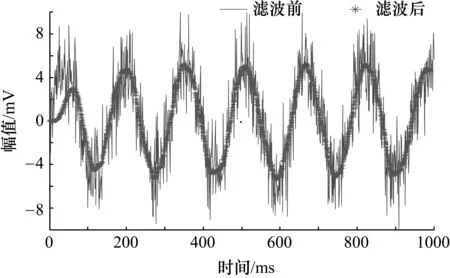
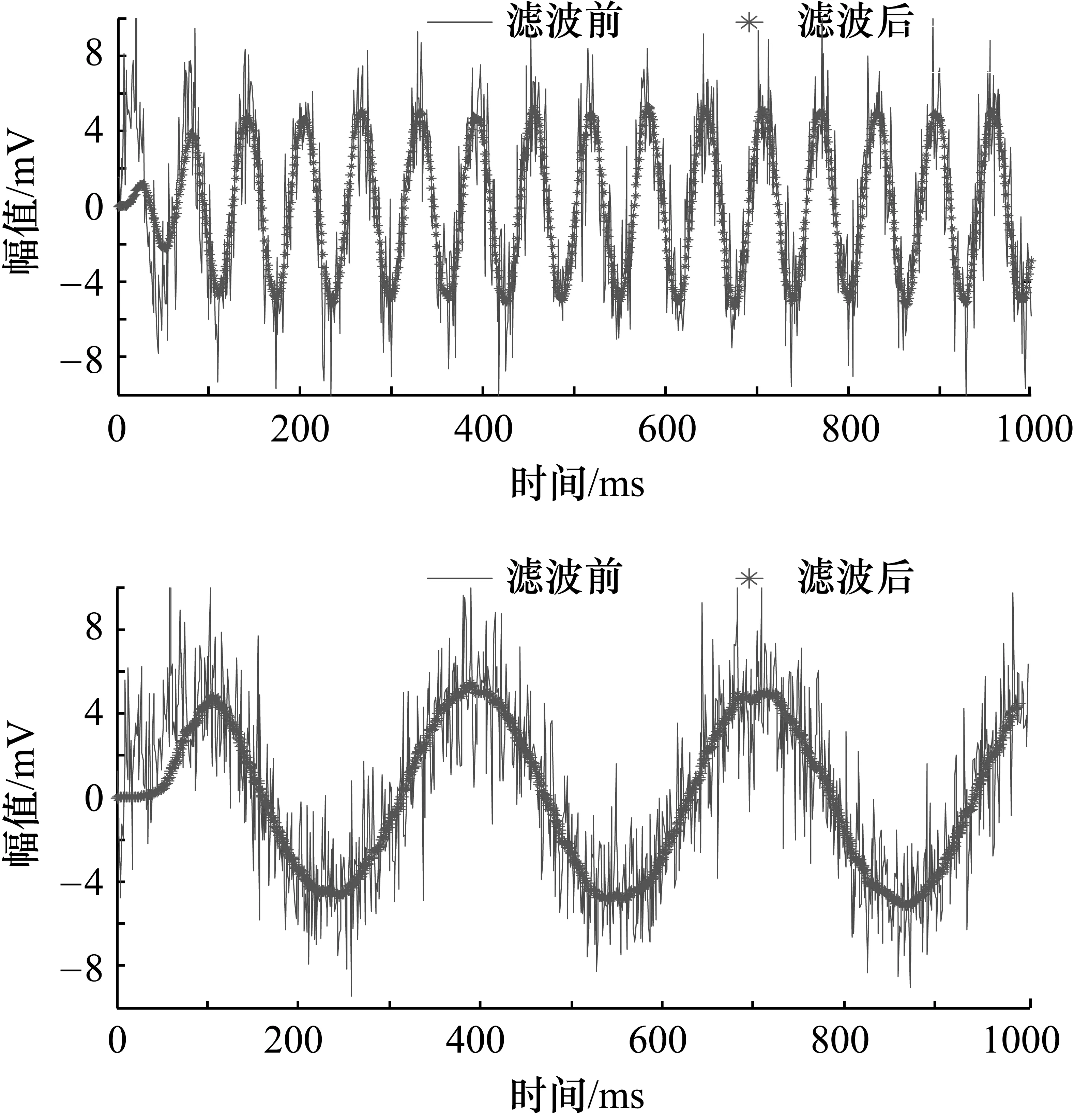
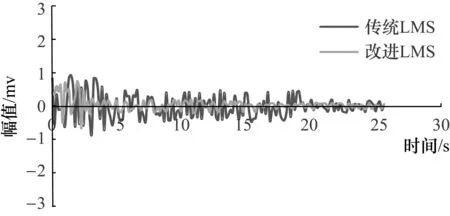
当步长因子满足0

0<β(1-exp(-α|e(n)|2))<1/λmax

(18)

即满足β<1/λmax时算法收敛。

在应用自适应滤波算法时，往往需要根据实际情况来选择调整步长因子以使系统的滤波效果达到最优，下面对改进的LMS自适应滤波算法在不同参数时的性能进行分析。

在满足收敛条件时，当式(18)中α参数固定时，随着β参数的增大，其收敛速度加快，根据实际情况，如果系统对收敛速度要求较高，可以选择较大的β值，如果系统对稳态误差要求较低，那么可以选择较小的β值。同理可得，当β参数固定时，α参数值越大，收敛速度越快，其在误差接近零处收敛速度也较快，可以根据实际情况来自由选择参数值，使系统达到最好的效果。

4 改进的算法应用于交流阻抗法

在交流阻抗法中由于输入的交流信号幅值特别小，容易受到噪音信号的影响以及工频干扰导致采集的响应信号不准确。第3节中介绍变步长的LMS自适应滤波算法对于滤除干扰信号具有较好的性能，所以可以应用于交流阻抗法来测量钢筋的腐蚀参数。

因为施加信号和响应信号频率相同，所以根据施加信号的频率可得到期望信号的频率，响应信号是混杂了扰动信号的杂波，频率是不确定的，将响应信号作为滤波器的输入，采用改进的变步长的LMS自适应滤波算法之后，可以将干扰信号滤除掉，起到较好的滤波效果。

期望得到的响应信号应该为施加信号同频率的正弦信号，但是往往存在各种干扰信号，无法直接获取到有用信号。改进后的自适应滤波算法得到的信号波形与初始信号的对比如图5所示，在经过算法处理之后，信号稳定在4 mV左右，初始信号幅值在干扰信号作用下在10 mV左右，对比可见该算法的滤波效果显著。

图5 改进算法后的滤波前后对比图

在进行钢筋腐蚀测量时，施加信号是扫频信号，其频率是变化的，要从交流阻抗谱中得到钢筋混凝土体系与频率相关的信息，进而分析腐蚀参数，所以设计的自适应滤波器应该是对不同的频率都有较好的滤波效果，不同频率下滤波效果如图6所示，图中分别为高频和低频信号下的滤波效果图，可以看出，该算法所设计的自适应滤波器能对不同频率的信号起到显著的滤波效果，大大提高了钢筋腐蚀参数的测量精度。

图6 不同频率下滤波效果图

传统的LMS算法和改进的变步长LMS算法滤波之后的实验数据的误差对比如图7所示。

图7 误差对比图

由图7可见，基于改进的变步长LMS自适应滤波算法与传统LMS算法相比，其准确性和稳定性都有明显的提升，由此可见，基于改进的变步长LMS自适应滤波算法应用于交流阻抗法进行钢筋腐蚀参数的测量是一种有效且较为精确的方法。

5 结束语

交流阻抗法能有效测量钢筋腐蚀参数，其响应信号微弱，易受干扰，改进的LMS自适应滤波算法与传统的LMS算法相比减小了系统的稳态误差,将改进的自适应滤波算法应用于交流阻抗法测量钢筋腐蚀，大大提高了测量精度以及信噪比，减小了测量误差。仿真结果及实验数据表明：该自适应滤波算法对干扰信号的滤除作用十分有效，效果显著。