压-剪试件在动态加载下的力学响应分析
2019-09-19李林涛王志华
徐 磊,李林涛,王志华
(太原理工大学 a.机械与运载工程学院,b.应用力学研究所,c.材料强度与结构冲击山西省重点实验室,太原 030024)
TC4(Ti6Al4V)钛合金是一种(α+β型)两相钛合金,既有较高的强度,又有足够的塑性,且能长期在高温下工作,因而在航空、航天、船舶、化工以及兵器领域得到非常广泛的应用[1-2]。由TC4材料制作的构件在使用过程中经常会受到强动载荷作用,因此对TC4钛合金在动态压缩下的力学性能研究非常重要。
在实际应用中,材料受载乃至破坏的过程一般是处于复杂应力状态下,同时受到法向和切向的作用[3]。在复杂应力作用下,材料的变形和破坏模式等都表现出明显不同于理想加载情况的行为特征[4]。很大程度上,剪切对材料的破坏起了主要的作用[5]。研究压-剪复合加载下材料的力学性能,对正确和全面认识材料的本构行为、理解材料破坏机理更具有现实意义。目前对于材料在复杂应力状态下力学行为的研究主要通过改变试样的形状以及引入特定的加载装置来实现。郑文等[6]在SHPB 实验装置的基础上添加了一个具有对称倾斜端面的垫块来实现压-剪复合加载。ZHOU et al[7]通过设计具有一定倾斜角度的压头,由套筒固定进行试验,得到压缩-剪切复合应力关系。JIN et al[8-9]通过测试引入斜截面的圆柱形试样得到了其在压剪应力空间下的屈服轨迹。上述的方法都是通过摩擦力来提供切向力,当倾斜角度达到一定程度时会出现滑动,切向力的位移计算就不再成立,此外还需要设计特定的加载装置。
本文主要基于RITTEL et al[10]设计的一种剪切压缩试件(SCS)进行数值模拟分析,讨论试件几何尺寸(长径比、根角半径、厚度)对SHPB实验结果的影响,以优化试件的几何尺寸参数;对试件内部应力状态的变化进行分析,并探讨运用SCS试件获得材料屈服面的可行性。
1 有限元模型的建立
1.1 几何模型
有限元模拟采用ABAQUS软件的Dynamic Explicit模块,建立分离式Hopkinson压杆(SHPB)装置的有限元模型,模型包括入射杆、透射杆和试件3个部分。其中:入射杆的半径r=6 mm,长度L=1 200 mm;透射杆的半径r=6 mm,长度L=1 100 mm;试件的几何模型如图1(a)所示。由于TC4钛合金金属在动态绝热剪切状态下会发生大变形和破坏[11],数值模拟过程中需尽量采用小的有限元单元尺寸,故对SCS倾斜段的单元进行局部细化加密,控制单元类型采用C3D8R八节点线性六面体单元。
由于撞击杆仅仅起到在入射杆中产生冲击应力波的作用,为了简化模型、提高计算效率、减少计算时间,此在SHPB有限元模型中省掉了撞击杆,直接在入射杆的一端施加沿杆截面均匀分布的应力波。入射杆端部输入的应力波脉冲通过实验测得,如图2所示。
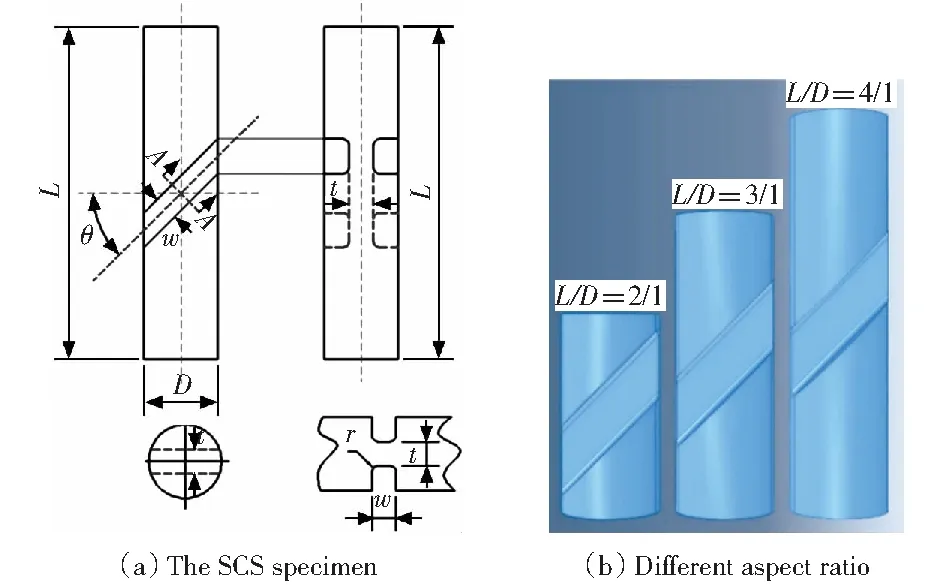
w=Slot width,t=Gage thickness,D=Diameter,L=Length,r=Root corner radius图1 SCS几何模型Fig.1 SCS geometric model

图2 入射应力波Fig.2 Incident stress wave
1.2 材料模型
有限元模拟过程中采用了两种材料模型:
1) 各向同性弹性模型。用于模拟入射杆和透射杆的材料为高碳钢,其材料参数为密度ρ=7 890 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3.
2) Johnson-cook本构模型和失效模型。Johnson-cook模型能够反映应变硬化、应变率硬化和温度软化效应,故采用本构模型描述TC4钛合金的应力-应变特性,失效模型描述该材料的损伤失效行为。其中TC4钛合金材料本构参数采用文献[12]结果,失效参数采用文献[13]的结果,具体参数如表1所示。

表1 TC4钛合金的材料参数Table 1 Material parameters of TC4
2 数值模拟结果与分析
运用SHPB系统进行分析需要满足两个基本假设:1) 一维应力波假设;2) 应力均匀性假设。只有在满足两个基本假设的前提下,获得的实验数据才具有可靠性。为保证两个基本假设满足,需要对试件两端的接触力进行动态力平衡验证[14],即任意时刻试件都处于左右两侧受力平衡的状态。动态力平衡公式如下:
Finput(t)=Foutput(t) .
(1)
式中:Finput和Foutput分别为试件左、右两个界面上的力。
为了选取满足SHPB动态测试两个基本假设的压剪试件,分别对不同长径比、根角半径、厚度的试件进行数值模拟分析。
2.1 试件长径比对两个基本假设的影响
对金属材料进行SHPB动态力学性能测试,为了减小惯性和摩擦力对试件在动态下应力测量的影响,DAVIES et al[15]提出了SHPB试样的最佳长径比为L/D=(3v)1/2/2,其中υ为泊松比。然而考虑到SCS试件开槽的影响,试件的长径比受到限制,故分别选取3种不同长径比(2∶1,3∶1,4∶1)的试件如图1(b),SCS的几何参数为:长度L=12,18,24 mm;直径D=6 mm;θ=45°;宽度b=3 mm;厚度d=1.5 mm;根圆半径r1=0.3 mm.进行Hopkinson-bar动态数值模拟分析,通过是否满足动态力平衡来验证压剪试件尺寸选取的合理性。不同长径比下试件和入(透)射杆杆端的接触力-时间变化曲线图如图3所示。

图3 不同长径比的接触力-时间变化曲线Fig.3 Contact force-time curves under different aspect ratios
通过对试件端面和入(透)射杆端面接触力-时间变化曲线分析可知,随着长径比的增加试件两端的接触力-时间变化曲线重合度越来越低,即保持动态力平衡能力较差,获得实验结果的可靠性降低。为了使压剪动态测试的实验结果更具可靠性,应该适当减小试件的长径比。综上可知,在3种长径比的压剪试件中长径比为2∶1试件的接触力-时间变化曲线重合度最高,故选取该长径比试件进行SHPB动态测试获得的实验数据更具可靠性。
2.2 试件根角半径、厚度对两个基本假设的影响
基于上文中提到更加符合动态力平衡的试件(长径比2∶1),接下来讨论不同根角半径、厚度的试件是否满足两个基本假设。分别加工3种厚度d(1.5,2.0,2.5 mm)及3种根角半径r2(0.3,0.9,1.5 mm)共计9种不同规格的压剪试件进行Hopkinson-bar动态数值模拟分析,通过是否满足动态力平衡来验证压剪试件根角半径和厚度选取的合理性。试件和入(透)射杆杆端的接触力-时间变化曲线如图4所示。
图4为不同根角半径、厚度的试件端面和入(透)射杆端面接触力-时间变化曲线,通过对入射端和透射端接触力-时间曲线的重合度来验证是否满足动态力平衡条件。考虑到SHPB数值模拟的过程相比实验过程更加理想化,对入射端和透射端接触力-时间曲线的重合度要求较高。为了更加直观了解不同厚度d和根角半径r2的试件对动态力平衡条件满足情况,对图4中满足动态力平衡结果进行分类,如表2所示。
由表2可知,当试件根角半径r2=0.3 mm时,3种厚度的试件进行动态测试时试件两端接触力都能保持平衡,均满足动态力平衡的条件。当试件根角半径r2=0.9 mm时,厚度d=2 mm的试件满足动态力平衡的条件;而厚度d=1.5,2.5 mm的试件不满足动态力平衡条件。当试件根角半径r2=1.5 mm时,厚度d=2.5 mm的试件满足动态力平衡的条件,厚度d=1.5,2.0 mm的试件均不满足动态力平衡的条件。通过上述数值模拟结果可知,试件倾斜段根角半径、厚度的选取对Hopkinson-bar动态测试的两个基本假设均有很大影响。因此,在设计试件尺寸时需要考虑试件倾斜段根角半径、厚度的参数。通过对动态力平衡验证结果分析可知,倾斜段根角半径r2=0.3 mm的试件不受厚度变化的影响且均满足动态力平衡,故该根角半径的选取更具普适性和合理性。
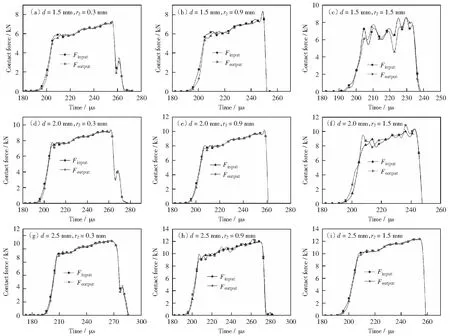
图4 不同根角半径、厚度下的接触力-时间曲线Fig.4 Contact force-time curves under different root angles and thicknesses

表2 动态力平衡结果Table 2 Results of dynamic force balance
2.3 试件内部的应力状态分析
在满足SHPB动态测试两个基本假设的前提下,对试件倾斜段的应力状态进行进一步分析。分别沿两个根角边缘和中部3个路径等间距取点,取点示意图如图5所示。各点Mises应力-时间变化曲线及Hopkinson-bar和试件的应变-时间变化曲线见图6和图7;试件整体的Mises应力、等效塑性应变云图见图8.
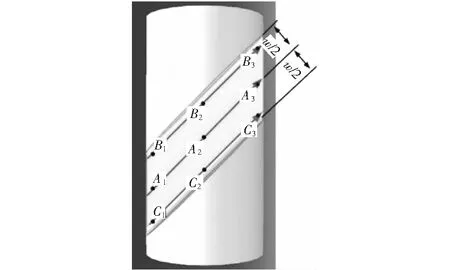
图5 试件取点示意图Fig.5 The points of SCS

图6 试件取点的Mises应力-时间变化曲线Fig.6 Mises stress-time curves with the points of SCS

图7 Hopkinson-bar和试件的应变-时间变化曲线Fig.7 Strain-time curves of Hopkinson-bar and SCS
由图5试件取点示意图及图6各点Mises应力-时间变化曲线可知,在弹性变形OA段,选取的9个点的应力随时间变化基本一致;当进入塑性变形AB段后,选取的点的应力发生变化,在根角点B1、C3位置处的应力随时间变化曲线最高,而B3、C1位置处的应力随时间变化曲线最小,其余各点的Mises应力强度和变化基本保持一致,且强度值介于两根角点强度值之间。因为在压缩-剪切复合应力下具有一定倾斜角试件的短对角上会出现应力集中[16],所以在根角线上会出现应力分布不均匀现象,短对角点位置上应力强度值较大而长对角点位置应力强度值较小。由图7可以看出,由入射杆、透射杆上得到的应变随时间变化曲线和试件倾斜段上的应变随时间变化曲线基本一致,说明在加载过程中由杆上获得应变信号能准确反映试件内部的应变状态。从图8 Mises应力和等效塑性应变云图很明显的看出,整个试件的塑性变形区和高强度值区域均集中在倾斜段,倾斜段除了因为应力集中效应导致出现较大应力和塑性应变的根角部位外,其余区域的应力和塑性应变分布比较均匀。综合图6各点Mises应力-时间变化曲线、图7 Hopkinson-bar和试件的应变-时间变化曲线和图8为试件整体的Mises应力、等效塑性应变云图可知,虽然两根角处会发生应力应变集中,但是在两个根角之间区域应力应变场分布比较均匀,满足试件均匀性假设。

图8 Mises应力和等效塑性应变云图Fig.8 Mises stress and equivalent plastic strain cloud
2.4 TC4的动态屈服准则
由以上分析结果确定了满足SHPB结果分析基本假设的试件尺寸参数,在加载过程中试件的变形主要集中在倾斜段,且满足试件均匀性假设的要求。为获得材料的屈服面,分别对不同倾斜角(0°,15°,30°,45°)的SCS试件(L∶D=2∶1,r2=0.3 mm,d=1.5 mm)进行动态、静态压缩数值模拟,将动态加载过程中得到的应变通过SHPB分析的三波公式换算成试件整体应力-应变曲线[17],得到试件动态下的应力-应变曲线和静态加载下的力-位移曲线如图9,图10所示。其中,三波公式为:
(2)
(3)
式中:εi(t)、εr(t)、εt(t)、SS、LS表示试件中的入射脉冲、反射脉冲、透射脉冲以及试件截面积和长度;而C0、E、SB则表示杆的弹性压缩波波速、弹性模量和截面积。

图9 动态加载下法向应力-应变曲线Fig.9 Dynamic normal stress-strain curves
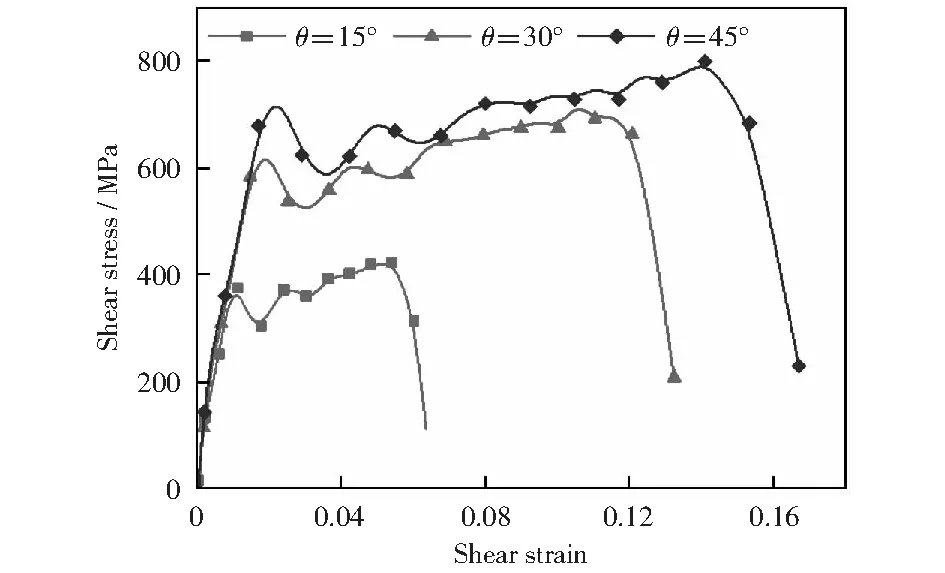
图10 动态加载下切向应力-应变曲线Fig.10 Dynamic shear stress-strain curves
在加载过程中入射杆端面受均布力F0,试件内部的压剪区分别受到垂直于倾斜方向的法向力Fn和平行于倾斜方向的切向力Fs,试件受力分析如图11所示,试件的变形如图12所示,压剪区沿轴向F0方向受力平衡,因此可知:
(4)
当试件沿轴向F0方向移动距离Δd时,试件的法向应变和切向应变分别表示为:
(5)
当试件处以弹性状态,此时可得到法向力和切向力满足的关系式:
Fn=σAs=EεAs.
(6)
Fs=τAs=GγAs.
(7)
式中:σ和τ分别为正应力和切应力;E和G分别是材料的弹性模量和剪切模量;As是试样倾斜段的斜截面面积。联立式(3),(4),(6),(7)可以得到动态复合压剪加载条件下的试样的正应力和切应力:
(8)
(9)
结合式(2)、式(5)可以得到压剪区的轴向应变和切向应变得表达式为:
(10)
(11)
因此将动态加载下的入射应变、反射应变、透射应变以及静态加载下的力和位移数据通过式(2)-(11)可以得出动态、静态复合应力状态下试件的正应力-正应变曲线、剪应力-剪应变曲线,如图9-10及图13-14所示。

图11 试件受力分析图Fig.11 Force analysis for specimen

图12 试件变形示意图Fig.12 Distortion analysis of specimen
图15-16为不同倾斜角试件的应力-应变曲线和力-位移曲线。由图可知,在弹性阶段,随着倾斜角度的增加试件的弹性模量不变;当进入塑性变形阶段,随着倾斜角度的增加,试件的屈服强度、极限强度明显下降,试件的承载力下降。对比图9、13法向应力-法向应变曲线和图10、14切向应力-切向应变可知,法向应力随倾斜角的增加而下降,而切向应力随倾斜角的增加而增大,所以随着倾斜角度的增加,试件的剪切效应越来越强;动态加载下的法向应力和切向应力强度值明显高于静态加载下的强度值;随着倾斜角度的改变,试件内部的应力状态虽然发生改变,但是弹性模量和剪切模量均不改变。
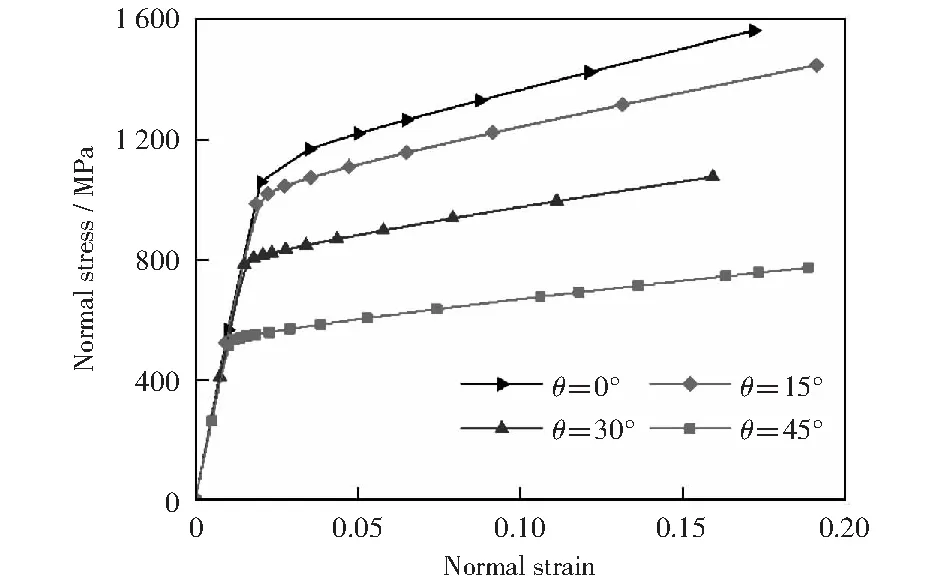
图13 静态加载下法向应力-应变曲线Fig.13 Quasi-static normal stress-strain curves

图14 静态加载下切向应力-应变曲线Fig.14 Quasi-static shear stress-strain curves
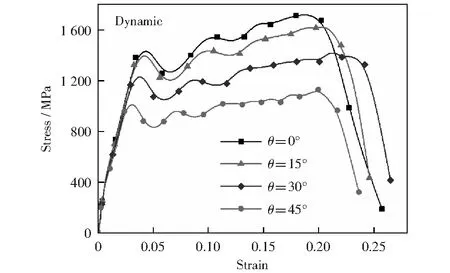
图15 不同倾斜角动态下试件的应力-应变曲线Fig.15 Stress-strain curves under different inclination angles
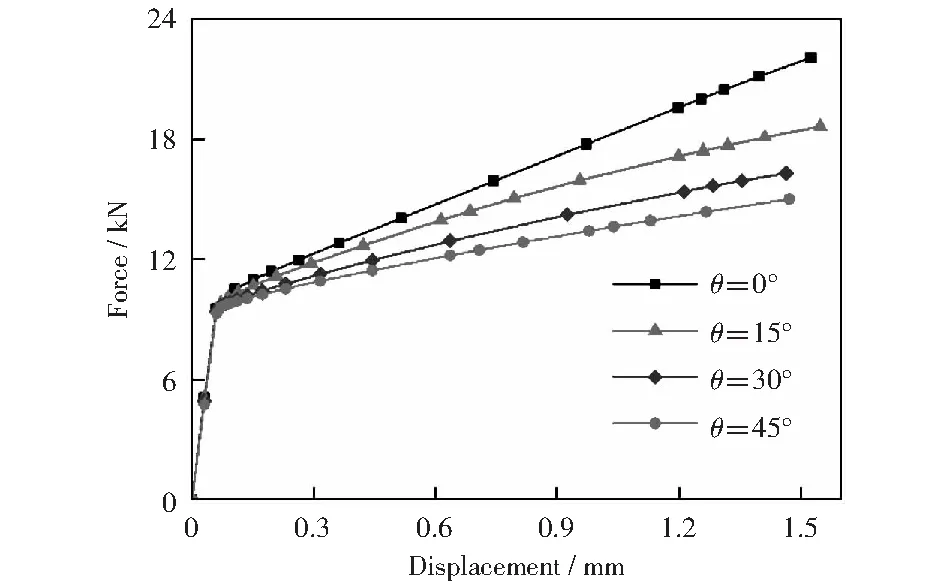
图16 不同倾斜角试件的力-位移曲线Fig.16 Force-displacement curves under different inclination angles
当材料发生塑性变形后,式(6)-(7)就不再满足,所以图9,10,13中曲线的塑性部分也就只具有参考意义。但是由法向应力-法向应变曲线、切向应力-切向应变曲线可以获得不同倾斜角度下的屈服强度,而通过不同的倾斜角度可以确定屈服面上的一个点。因此得到TC4钛合金的屈服面,如图17所示。
图17中两条曲线为理论计算的动、静态屈服面,直线0°,15°,30°,45°分别为对应倾斜角时的加载路径。由图17可知,不同加载路径下得到的屈服应力和理论值一致,说明此种SCS试件能得到有效的动、静态屈服面,可用来研究材料的屈服准则。
3 结论
本文基于SHPB数值模拟分析了SCS试件在压-剪复合加载下获得材料屈服面的可行性。通过对数值模拟结果分析得到了如下结论:
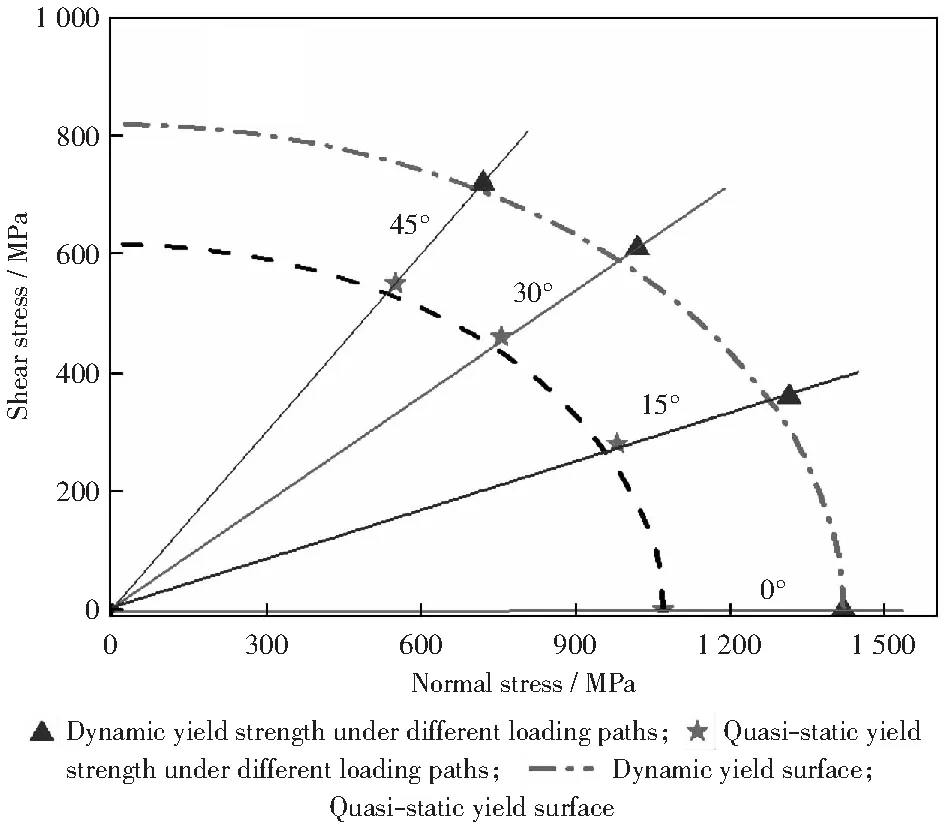
图17 压-剪复合加载下试件的静态、动态屈服面Fig.17 Quasi-static and dynamic yield surface of specimen under combined shear-compression
1) SCS试件长径比以及倾斜段的根角半径、厚度均对SHPB结果分析有影响,在运用SHPB分析时需要对SCS试件进行设计并验证动态力平衡。
2) SCS试件的塑性变形区主要集中在倾斜段,倾斜段在加载过程中应力-应变场均匀分布,满足试件均匀性假设。
3) 通过分析不同倾斜角度下SCS试件的法向应力-应变关系和切向应力-应变关系,获得不同应力加载路径下材料屈服强度的法向分量和切向分量,可以确定材料的准静态和动态加载屈服面,这对于研究材料的屈服准则有非常重要的意义。
