高地应力深部巷道变形破坏特征的相似模拟实验研究

薛光武

(1.吕梁学院 矿业工程系，山西 吕梁 033001；2.太原理工大学 矿业工程学院，太原 030024)

随着我国煤炭开采强度的不断增大，地下浅埋深煤炭资源日益枯竭，急需发展深部煤层开采工艺[1-4]。然而在开采深度增加的同时，产生了一系列复杂棘手的问题：

1) 围岩地应力剧烈增加。围岩在高地应力作用下发生能量集聚现象，在外界扰动的影响下就可能会发生岩爆现象。此外，在高剪切力和拉应力的作用下，围岩会发生挤压大变形。这些因素导致围岩内部产生一系列复杂多变的孔裂隙，并造成围岩的力学强度大大降低，不利于巷道的稳定性和安全性[5-7]。

2) 在深部高地应力条件下，围岩应力的释放以及能量的转化致使围岩内部产生一系列互相交替的破裂区和非破裂区，而基于传统的连续介质弹塑性力学理论并不能对此进行合理的解释。例如，传统弹塑性力学仅仅能反映出岩石在峰值之前的物理力学性质，对于峰后阶段岩石内部微裂隙扩展、演化以及闭合并不能如实反映出来[8-9]。

3) 深部围岩的分区破坏方式与传统的围岩破坏“三带”划分不一致。

针对上述问题，已有学者通过室内试验和数值模拟进行了研究。汪斌等[6]探讨了深埋工程岩体开挖后围岩的强度特征。吕颖慧等[7]基于室内试验得出，巷道围岩的破坏方式随着地应力的增大逐渐由脆性向韧性转化。赵瑜等[10]采用数值模拟探讨了深埋隧道围岩巷道的局部破坏和渐进破坏机理。上述学者的研究均是集中于对围岩在高应力条件下的破坏方式和特征上，对于高地应力条件下巷道围岩的整体运移规律和垮塌机理缺乏阐述和总结。此外，上述试验现象和研究结论仅仅适用于双向地应力条件，对于含有自由面的围岩并不适用。综上所述，为了保证深部高地应力巷道的稳定性和安全性，急需对围岩的变形破坏规律进行研究。为此，本文基于高应力二维相似模拟实验台，对某煤矿埋深847 m的巷道进行了相似模拟实验，重点分析了围岩应力分布和位移分布规律。

1 实验方案

本文以某煤矿运输大巷为实验原型。该巷道埋深为847 m；几何形状为矩形，高为4.2 m，宽为5.4 m.巷道所在的岩层为粉砂岩，平均抗压强度为87.5 MPa.巷道顶板为细砂岩，硬度较大，颗粒之间比较致密，平均抗压强度为56.4 MPa.底板为中砂岩，该岩层呈层状结构，颗粒粒径较小，平均抗压强度为48.9 MPa.在相似模拟设计中，相似模型的几何相似比为30，即模型巷道的宽×高=167 mm×133 mm；容重相似比为1.67，应力相似比为50，时间相似比为5.48.真实地层中垂直应力为25.23 MPa，水平应力为27.75 MPa.经计算得到油缸垂直供压值为7.17 MPa，水平方向油缸供压值为7.89 MPa.

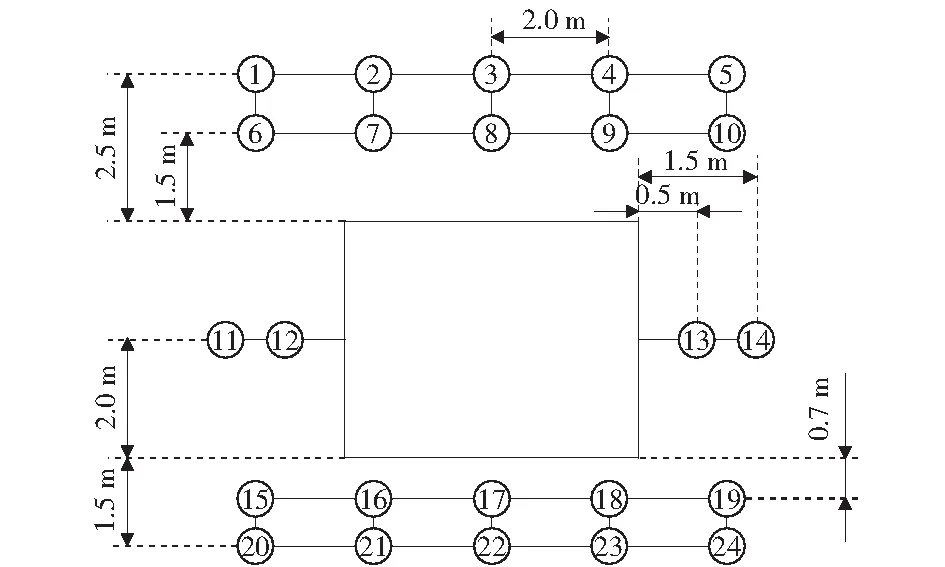
图1 位移测点布置图Fig.1 Arrangement of displacement measuring points

应力盒在模型中的布置位置如图2所示。按几何相似比折算成原型尺寸。其中，巷道中线左侧区域测点用来测量水平应力，巷道中线右侧区域测点用来测量垂直应力。

图2 应力测点布置图Fig.2 Arrangement of stress measuring points

对于相似材料的制备，本文选用细小河沙和石英作为骨料，石膏和石灰作为胶结物，云母粉作为岩层层理。由于石膏遇水硬化速率较大，在材料中添加了一定含量的缓凝剂，以便于降低硬化速率。

2 实验结果与分析

2.1 巷道围岩位移分析

巷道围岩的位移变化量与巷道的稳定性和安全性紧密相关。为了实时观察围岩的变形规律，本文在巷道围岩四周布置了一系列的位移监测点，着重分析了巷道围岩的顶板垂直位移、巷道底板垂直位移和巷道两帮水平位移随时间的变化规律。

2.1.1巷道顶板垂直位移

由图3可知，巷道顶板的沉降量随着时间的增加而逐渐增大，然而每排测点的位移监测数据却有较大的差异。图3(a)中，第一排的位移监测点(测点1-5)从开始监测到监测结束，位移变化量较小，最大位移下沉量为9.2 mm.图3(b)为第二排的位移监测数据(测点6-10)，在开挖12 d内变化不明显；在开挖12 d之后位移发生突变，下沉量出现了较大的变化；在开挖42 d时位移绝对值达到最大值，该值为234 mm.

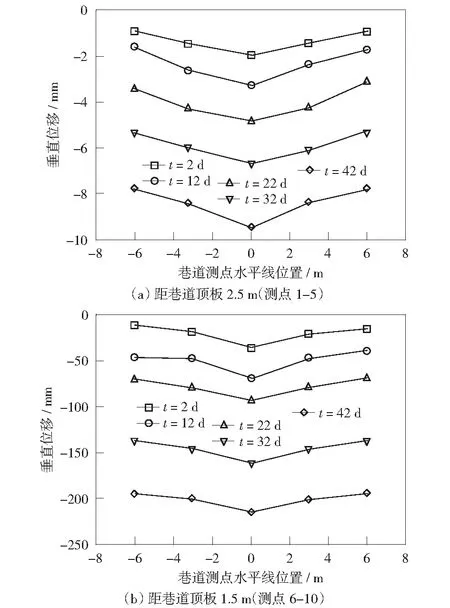
图3 巷道顶板不同层位围岩的垂直位移Fig.3 Vertical displacement of surrounding rock in different layers of tunnel roof

2.1.2巷道两帮水平位移

图4为巷道围岩两帮中部监测点(测点11-14)的位移量随时间的变化曲线。从图中可以得出：随着开挖时间的增加，围岩两帮向内部移进量逐渐增大，然而不同监测点处的位移变化程度大为不同。监测点11与14从开挖之初至开挖12 d，位移变化量相对较小，最大变化量分别为18.4 mm与18.8 mm.对于监测点12与13来说，围岩位移变化量非常明显，其最大移进量分别为162 mm与154 mm.由此可以得出，越接近于巷道两帮的位置，其位移变化程度越明显。

图4 巷道两帮不同部位围岩的水平位移Fig.4 Horizontal displacement of surrounding rock in different parts of tunnel

2.1.3巷道底板垂直位移

图5分别为第四排位移监测点(测点15-19，在巷道底板下方0.7 m处设定)和第五排位移监测点(测点20-24，在巷道底板下方1.5 m处设定)的垂直位移随时间的变化曲线。从图5可以得出：随着开挖时间的增加，地板向上鼓起量逐渐增大；不同监测点的位移变化程度大为不同。图5(a)显示：在开挖12 d之前底板鼓变形不明显；12 d之后巷道底板鼓起量迅速增大，并且在42 d时达到最大值(154 mm).图5(b)显示：从巷道开挖之初到开挖12 d的位移变化量均非常小；在42 d之后，位移绝对值最大值约为10.3 mm.需要注意的是，底板右半部分的移进量要大于底板左半部分，这主要是因为底板发生了剪切变形破坏。

对照组患儿采用沙美特罗替卡松结合糠酸莫米松治疗,沙美特罗替卡松吸入剂(Glaxo Operations UK Limited国药准字H20150242规格50ug/500ug*60泡),早晚1次。糠酸莫米松鼻剂(Schering-Plough Labo N.V.(比利时)国药准字H20140100),每侧鼻孔1揿,每日1次,持续治疗30d。

图5 巷道底板不同层位围岩的垂直位移Fig.5 Vertical displacement of surrounding rock in different layers of tunnel floor

2.2 巷道围岩应力分析

巷道开挖之后，每隔10 min对各个监测点的水平应变量和垂直应变量进行统计，然后再将该应变量代入到相应的公式中反算，得出水平应力值和垂直应力值。本节重点分析了巷道顶底板、巷道两帮的应力变化规律。

2.2.1巷道顶板应力

图6(a)为巷道顶板两个不同监测点的垂直应力随时间的变化图。监测点4′处的垂直应力绝对值从整体上看随时间的增加而逐渐降低；在开挖12 d之前，下降率比较大；在开挖12 d之后下降趋势逐渐缓和；在巷道开挖20 d后应力趋于稳定，绝对值达到11.17 MPa.监测点2′处的垂直应力绝对值从整体上看随着时间的增加逐渐降低，在巷道开挖42 d后其值达到27.60 MPa.

图6(b)为巷道顶板两个不同监测点水平应力随时间的变化图。监测点3′处的水平应力绝对值从整体上看随时间的增加而逐渐降低；在开挖12 d之前，下降比较剧烈；在开挖12 d之后下降趋势逐渐缓和；在巷道开挖20 d后趋于稳定，绝对值达到15.37 MPa.监测点1′处的水平应力绝对值在开挖10 d以内随着时间的增加出现下降的趋势；在开挖12 d之后应力绝对值逐渐增大；在开挖42 d之后趋于缓和，应力绝对值达到56.50 MPa.由此可以得出，监测点3′处的岩体发生了屈服破坏，而监测点1′处的岩层处于应力集中区域。

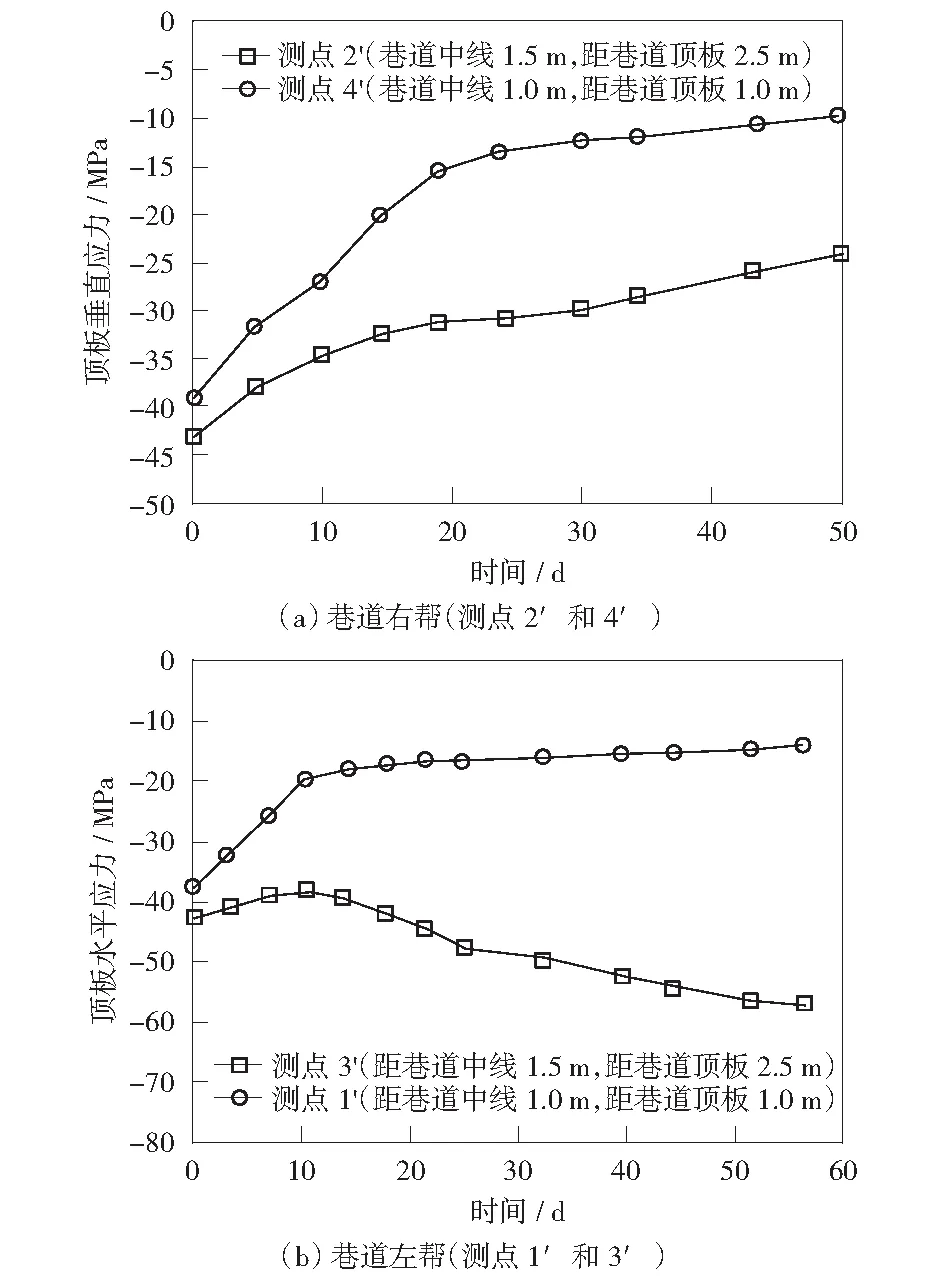
图6 巷道顶板垂直应力和水平应力与时间的关系曲线Fig.6 Change of vertical stress and horizontal stress of tunnel roof with the time

2.2.2巷道两帮应力

图7(a)为巷道围岩两帮不同监测位置处的垂直应力随时间的变化曲线。监测点7′处的垂直应力绝对值从整体上看随着时间的增加而逐渐下降；在开挖42 d之后逐渐趋于稳定，达到15.55 MPa.监测点8′处的垂直应力绝对值在巷道开挖15 d之内随着时间的增加而逐渐降低；在开挖15 d之后随着时间的增加又逐渐增大，并在开挖42 d后趋于稳定，达到76.50 MPa.由此可知，监测点7′处的岩层已经发生了屈服破坏，应力逐渐向深部转移，而监测点8′处的岩层属于应力集中区域。

图7(b)为巷道围岩两帮不同监测位置处的水平应力随时间的变化曲线。从整体上看，监测点6′处的水平应力绝对值随着时间的增加而逐渐下降；开挖16 d之前下降程度比较剧烈；开挖16 d之后下降速率缓和；在开挖42 d之后趋于稳定(绝对值达到4.52 MPa).监测点5′处的水平应力绝对值随着时间的增加而逐渐降低，并且在开挖42 d后趋于稳定，达到13.90 MPa.

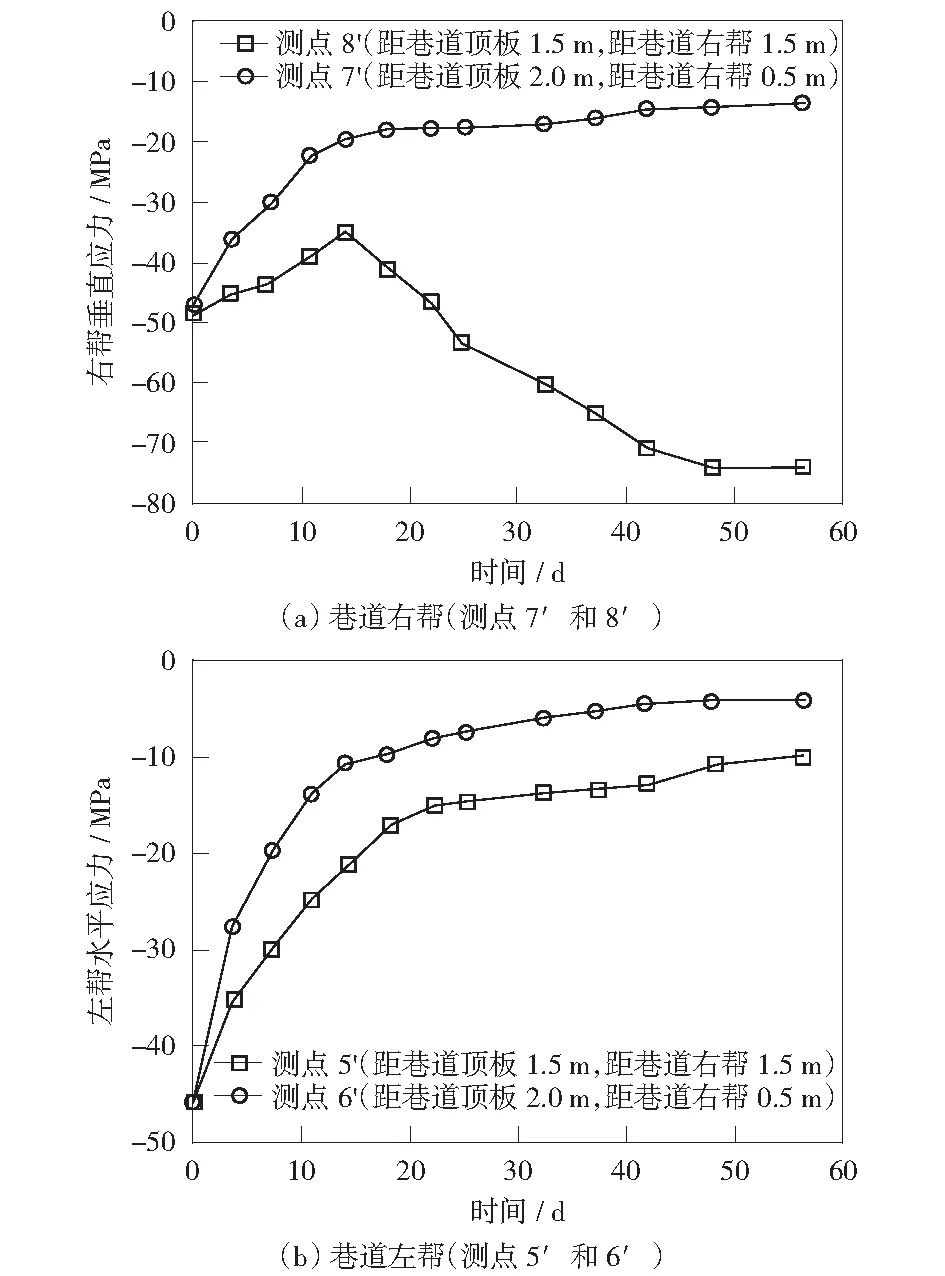
图7 巷道两帮垂直应力和水平应力随时间的变化Fig.7 Change of vertical stress and horizontal stress of two sideways in tunnel with the time

2.2.3巷道底板应力

图8(a)为巷道底板不同监测位置处(10'和12')的垂直应力随时间的变化曲线。两个监测点处的垂直应力绝对值均随着时间的增加而逐渐下降；在开挖17 d以内下降程度比较剧烈；在开挖17 d之后下降程度趋于缓和；在开挖42 d后趋于稳定，应力绝对值分别为4.35 MPa(测点12′)和18.60 MPa(测点10′).

图8(b)为巷道底板不同监测位置处的水平应力随时间的变化规律。监测点9′处的应力绝对值随着时间的增加而逐渐下降，并在开挖42 d后趋于稳定，达到16.30 MPa.监测点11′的水平应力绝对值在开挖15 d以内逐渐下降；在开挖15 d之后又逐渐增大；在开挖42 d后趋于稳定，达到51.60 MPa.由此可知，监测点9′处的岩层已经发生了屈服破坏，而监测点11′处的岩层属于应力集中区域。

3 结论

针对某煤矿深部高地应力巷道的安全支护问题，本文通过自行设计的二维高应力相似模拟实验平台，对该巷道围岩的破坏变形规律，以及位移和应力分布规律进行了试验研究，主要结论如下:

图8 巷道底板垂直应力和水平应力随时间的变化Fig.8 Change of vertical and horizontal stress of tunnel floor with the time

1) 该巷道在开挖完毕之后，随着时间的增加，变形破坏范围逐渐增大。在顶板的冒落范围延伸到上覆第二岩层的位置处，冒落区域呈现拱形。巷道两帮由于挤压发生严重的变形；在顶板和围岩两帮局部位置出现了一系列相互交叉贯通的复杂裂隙带；底板由于剪切错动发生了底鼓现象。

2) 巷道顶板上方1.5 m处的岩层位移下沉量约为 234 mm；巷道围岩左右两帮0.5 m处的岩层向内部移进量分别为162 mm，154 mm； 底板下方0.7 m处的岩层向内鼓起量为154 mm.

3) 巷道顶板上方2.5 m处的岩层稳定后的水平应力绝对值为15.37 MPa；巷道两帮1.5 m处的岩层稳定后的垂直应力绝对值为15.55 MPa；底板下方1.5 m处的岩层稳定后的水平应力绝对值为16.30 MPa.