Pre-stack seismic waveform inversion basedon adaptive genetic algorithm

LIU Sixiu, WANG Deli and HU Bin

College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China

Abstract: Pre-stack waveform inversion, by inverting seismic information, can estimate subsurface elastic properties for reservoir characterization, thus effectively guiding exploration. In recent years, nonlinear inversion methods, such as standard genetic algorithm, have been extensively adopted in seismic inversion due to its simplicity, versatility, and robustness. However, standard genetic algorithms have some shortcomings, such as slow convergence rate and easiness to fall into local optimum. In order to overcome these problems, the authors present a new adaptive genetic algorithm for seismic inversion, in which the selection adopts regional equilibrium and elite retention strategies are adopted, and adaptive operators are used in the crossover and mutation to implement local search. After applying this method to pre-stack seismic data, it is found that higher quality inversion results can be achieved within reasonable running time.

Keywords: genetic algorithm; adaptive probability; regional equilibrium; seismic inversion

0 Introduction

Seismic inversion is divided into two sections, pre-stack seismic inversion and post-stack seismic inversion. Pre-stack seismic inversion has high resolution and can provide detailed reservoir information, but it faces four fundamental problems (Luoetal., 2006): ①computational volume and data volume are very large; ②data and model are highly nonlinear; ③the objective function has multiple minimum values; ④there will be multiple solutions (Fu & He, 2002). In recent years, a large number of researches have been conducted to overcome the above issues. For example, the nonlinear inversion method using genetic algorithm (GA) for global optimization has successfully solved the problem of high nonlinearity between the data and the model as well as multiple minimum values of the objective function in pre-stack seismic waveform inversion. Genetic algorithms are gradually applied to the inversion of seismic data because of their advantages of not relying on the initial model and strong searching abilities. However, after the crossover probability and the mutation probability are fixed, there are non-convergence and premature convergence problems in the standard genetic algorithm (SGA). Therefore, a wealth of improvements has been made on SGA (Sunetal., 2017). Yuetal.(2014)proposed an improved genetic algorithm to solve the traveling salesman problem, in which the greedy algorithm was introduced to initialize the population on the basis of the traditional genetic algorithm. An improved hybrid genetic algorithm integrating heuristic algorithm, tabu search algorithm and simulated annealing algorithm has been put forward by Yao & Wang (2015).Caoetal. (2014) proposed an adaptive guided evolutionary genetic algorithm. Some other improved genetic algorithms have also been developed, which will not be listed here. Although a large number of improved genetic algorithms have been proposed in recent years, we have found that if the genetic operators can be dynamically adjusted according to the distribution of individuals, the diversity of individuals can be enhanced and the algorithm convergence can be accelerated. Therefore, this paper proposes an adaptive improved genetic algorithm to invert pre-stack seismic parameters including P-wave,S-wave velocities and density.

In the analysis and processing of geophysical data, inversion and forward performance are complementary. Of the current seismic waveform inversion methods, seismic wave forward modeling accounts for more than 95% of the total inversion calculation. The overall inversion efficiency mainly depends on that of the forward method. As a key step in seismic inversion, seismic wave forward modeling is an important issue to be taken into consideration. There are many methods for forward modeling. Among them, the ray method has a low computational cost and can deal with complex geological bodies. However, its accuracy is low, in particular in the presence of coupling between different types of waves in complex media. Despite the fact that the differential method has a wide range of applications and can accurately simulate seismic wavefield in any inhomogeneous medium, its calculation cost is high and it is required to meet the absorption boundary condition; the accuracy of the reflectivity method is higher than that of the ray method and the difference method (Fuchs&Muller,1971). Moreover, the reflectivity method involves multiple reflections and converted waves in the reflection layer and can provide full wavefield solution. Therefore the method becomes the most effective method to achieve the full wavelength simulation in the layered half-space medium, and it does not involve the procedure of grid dispersion and the boundary condition possessed by the finite difference method. Besides, the calculation efficiency of it is high without introducing noise (Li, 2013).

Therefore, this study combines the reflectivity forward modeling and the improved genetic algorithm. Firstly, the synthetic seismic trace obtained by the forward modeling of the reflectivity method is compared with the measured one. Secondly, the prior models are modified by the selection, crossover and mutation of the GA. Thirdly, forward calculation, matching, comparison and modification are iteratively performed to meet the end condition. The best result is then output. In this paper, the theoretical model is used to compare the inversion result of SGA with that of the improved method to verify the superiority of our method. Besides, our method is successfully applied to the measured pre-stack data of a certain area, and the practicability is proved.

1 Principle of reflectivity method

Several good books (Kennett&Kerry, 1979; Kennett, 1979) on the reflectivity method have been published, the details of the reflectivity method will not be described here. Instead, the three basic steps that dominate in this method (Chen, 2013) will be discussed.

1.1 The establishment of displacement function

To make it easier, we take the plane wave incident on the upper surface of the formation as an example to study the propagation of P and S waves. A layered model (Fig.1) is designed, for which the P and S wave velocities, density, and thickness of each layer are known. The interlayer consists ofn-1 horizontal layers, and the formation numbers are 1, 2, … ,n.

We first analyze an arbitrary layer, say, the layerk(Fig.2) and the displacement function expressions of each wave in the layerkare given as：

(1)

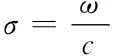
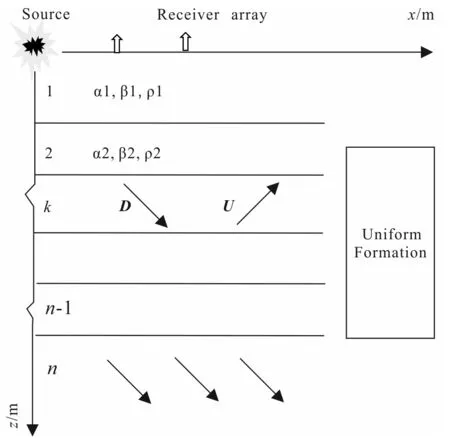
D and U correspond to the up-going and down-going waves, respectively.Fig.1 Schematic diagram of the layered model

Fig.2 Wave propagation in layer k

1.2 Reverse matrix

By the theory of seismic wave and the wave equation, the wave function in each layer should meet the boundary conditions at the interface:

(2)

Substitution of Eq.1 into Eq.2, followed by some mathematical derivations, leads to the formula for the relationship between the displacement and the stress on the top surface of each layer:

(3)

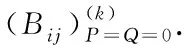
1.3 The obtainment of reflection coefficient

Suppose only P wave is incident on the interface, we have

(4)

(5)

The coefficientRPPof P-wave reflection in the frequency-slowness domain is obtained by substituting Eq.4 into Eq.5. Then it is multiplied by the seismic wavelet in the frequency domain to obtain the PP wave response in the frequency-slowness domain. Finally, the response is converted into a synthetic seismic record in the time-slowness domain (angle domain) by inverse Fourier transform.

2 Seismic waveform inversion based on adaptive genetic algorithm

It was Professor Holland of the University of Michigan who first proposed the genetic algorithm in 1975. First, all the encoded parameters are connected to form a chromosome according to the actual situation, and the initial population is randomly generated. Then, the chromosomes in the initial population experience copy, crossover, and mutation to generate the next new generation according to their own fitness value that determines the quality of the individuals. Finally, the above steps are repeated until our requirement is met. This paper proposes a seismic waveform inversion method based on adaptive genetic algorithm by using adaptive selection, crossover and mutation operators.

2.1 Fitness function

In the process of seismic data inversion, the parameters needed to find out are the velocities and density of the P and S waves of each layer. To make the individuals in the population adjust locally, the real number coding is used , that is, these three parameters are represented by their corresponding real numbers(Wang & Yang, 1998). To calculate the error, we first make an objective function:

objvalue=norm(rd-sd)

(6)

Whereobjvalue, the value of the objective function, represents the residual error between the synthetic seismic datasdand the real datardand should be as small as possible;normindicates that the objective function uses the norm of the error. The fitness function used here is (Yang, 2017):

Fit=1/(objvalue*objvalue+0.001)

(7)

WhereFit, which is essentially similar to the objective function valueobjvalue, is called the fitness function value and it determines each chromosome’s regeneration probability to enter the population. Usually the fitness function should be the objective function itself or another function with the objective function as an independent variable. It turns out that the greater the fitness of the chromosome, the higher its survival rate.

2.2 Adaptive selection operator based on regional equilibrium

The selection operator in GA retains the individuals with larger fitness values in the parents through some algorithm based on the fitness function, while others with lower fitness values will be eliminated. Included in the traditional selection operators are Roulette selection, random competition selection, sorting selection, random leagues, and so on. The preference one is the Roulette that finds out the probability that each individual in the current generation will be selected to enter the next generation according to the fitness value of their own(Fu & Wu, 2018). The probability that an individual is selected to be copied is:

(8)

Wherea(i) is the fitness value of thei-th individual in thej-th generation. Obviously, the larger the fitness value, the greater the probability of being selected and vice versa.

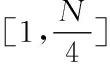
2.3 Adaptive crossover operator

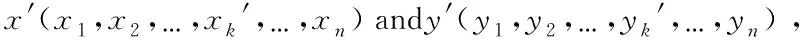
xk′=λxk+(1-λ)yk

yk′=λyk+(1-λ)xk

(9)

Whereλis a random number over the interval (0, 1).

It should be noted that in the traditional genetic algorithm, the crossover probability is a fixed value, which is between 0.1 and 0.9. It is simpler to use a fixed value of the crossover probability within this interval to materialize the crossover section, but this will lead to the loss of good genes in the individual, thus lowering the convergence of the algorithm. Therefore, the authors tried to improve the crossover operator in this paper: an adaptive crossover probability is used to make the individual’s crossover probability change with their fitness values, which improves the global optimization ability of the algorithm to some extent (Yeetal., 2009). In the improved adaptive genetic algorithm, the maximum and minimum values of the population crossover probability are set, and the minimum value is not equal to zero. When the individual population has the maximum fitness value, the process can still be performed with the minimum crossover probability, so that the individuals are not in a state of stagnation. The crossover probability formula becomes

(10)

WherePc1=0.99,Pc2=0.8, representing maximum and minimum crossover probability respectively;favgis the average fitness value of all individuals in the contemporary population;f′ is the larger fitness value for the two individuals that will intersect;fmaxrepresents the largest fitness in the population.

2.4 Adaptive mutation operator

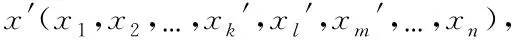
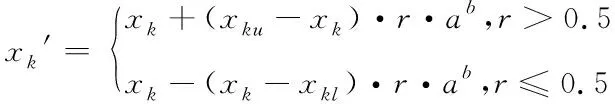
Where the value of the genexkis over the interval (xkl,xku);ris a random number lying between 0 and 1;a=(1-t/T),bis a system parameter over the interval (2,5);tis the current number of iterations; andTis the total number of iterations.

As mentioned before, this paper uses an adaptive approach to dynamically adjust the probability of variation for each individual in the current population (Maetal., 2017), namely

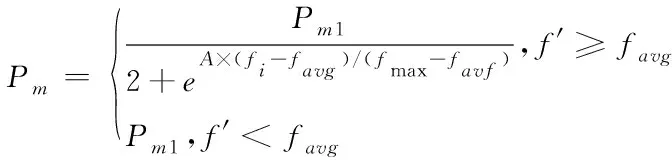
(12)

WherePm1=0.15，A=5,favgstands for the average fitness for all individuals in contemporary population;fishows the fitness value for the mutated individual;fmaxrepresents the largest fitness in the population.

2.5 Algorithm flow

The basic idea of pre-stack waveform inversion is to first establish a set of models by using prior information and perform forward calculation to obtain synthetic seismic traces, and then compare them with real seismic traces. By comparing, we iteratively update the models using our method and output the best inversion result in the end. The process of the exact inversion process is as shown in Fig.3 (Zhanetal., 2015).

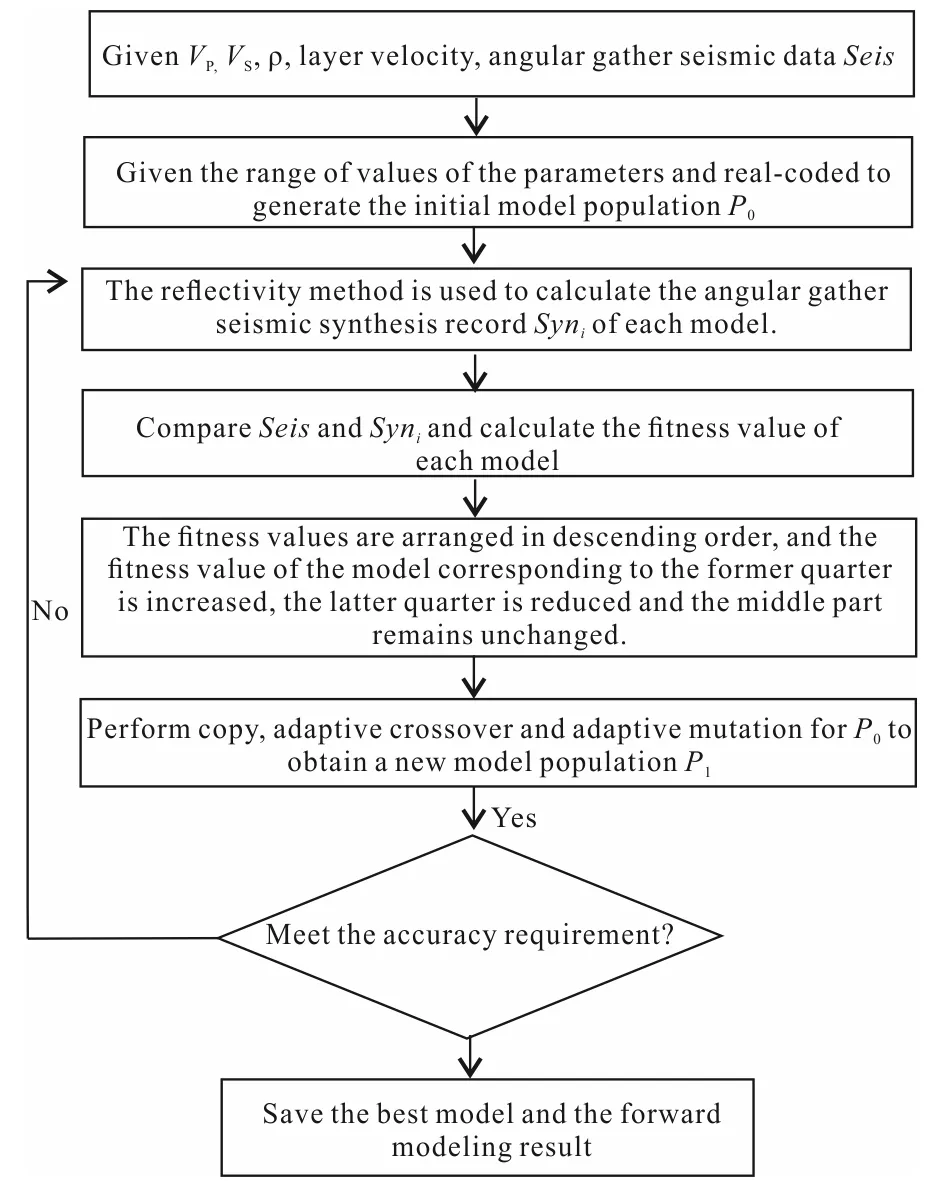
Fig.3 Flow chart of improved pre-stack waveform inversion (after Zhan et al., 2015)

3 Case study

3.1 Theoretical test

This study uses SGA and our improved method to test a layered model (Fig.4) .The parameters are defined as follows: the population size is 20 and the maximum number of iterations is 100. The simulation was carried out in Matlab environment.

Here we evaluate the convergence efficiency of the two algorithms based on the variation of the maximum objective function value and the average objective function value via the iteration in the evolutionary process. By comparison, it can be seen from Fig.5 that as the evolutionary generation increases, the maximum and average values of the objective function of the two algorithms tend to converge. Among them, the SGA begins to converge in the first 15 generations from 6.5 to 5.3, which is a premature phenomenon. And after that, the speed of declining slows down, the dynamic performance is unstable in the later stage, and it is not easy to find the optimal solution. However, the algorithm adopted in this paper starts to converge in the first 50 generations, and converge to 3.7 stably in the end, and it is not easy to fall into the local minimum. It can be inferred from the above comparison between the improved method and SGA that our improved method shows much more superiority than SGA.

Fig.6a-c shows the measured seismic record, the set of seismic traces obtained by SGA and the set obtained by our algorithm. It can be seen from Fig.6a and Fig.6b that the result of SGA inversion is not very satisfactory due to the fact that the forward result of SGA do not coincide well with the real data (Fig.6a). However, as can be seen from Fig.6a and Fig.6c, the time axes of the two seismic traces correspond well, which means a better result of our method than SGA.

3.2 Inversion of real data

The data needed to perform pre-stack waveform inversion are a pre-stack incident angular gather and velocity spectra. The gather requires a series of processing such as velocity analysis and dynamic correction. The initial model obtained is shown in Fig.7.We selected the M well in a study area to perform pre-stack waveform inversion and then analyzed the feasibility of our method by comparing the P and S wave velocities and density curves.

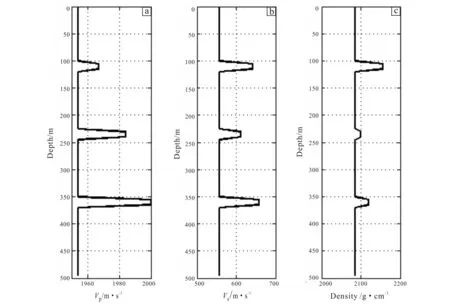
Fig.4 Curves of P-wave (a), S-wave (b) velocities and density (c) in layered model

Fig.5 Variation of optimal (a) and average (b) values of objective function for two algorithms

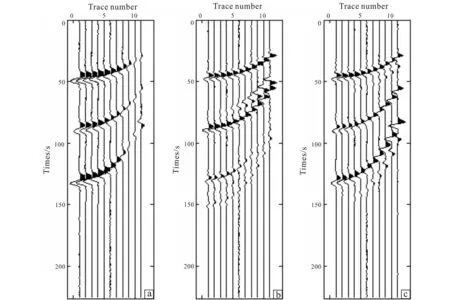
Fig.6 Different seismic records: (a) measurment in layered model, (b) inversion result by SGA and (c) that of improved method

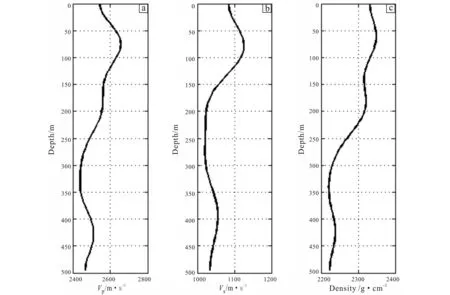
Fig.7 Initial model curves of P-wave (a), S-wave (b) velocities and density (c)

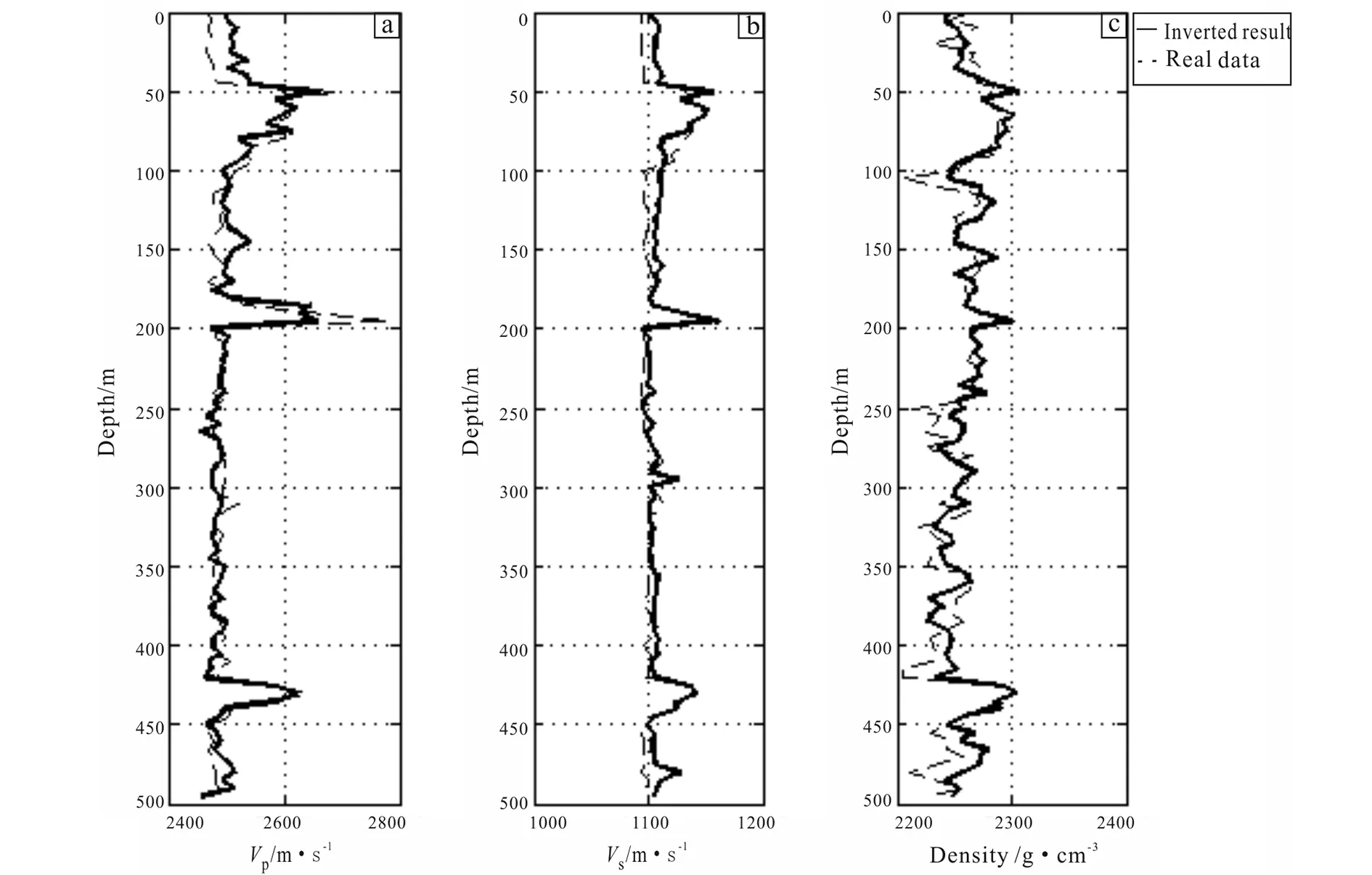
Fig.8 Curves of real well parameters and inverted result of improved method for P-wave (a), S-wave (b) velocities and density (c)

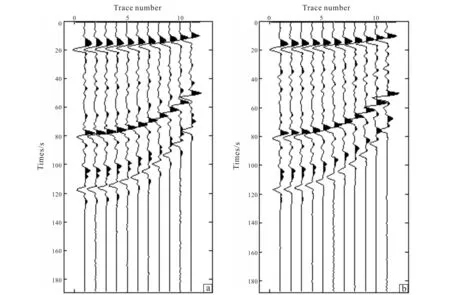
Fig.9 Comparison of actual seismic trace at M well (a) and synthetic seismic data of improved method (b)

From Fig.8, it can be seen that the inversion curve is still very comparable with the actual well curve, except a slightly larger difference between the two density curves, indicating that there is greater uncertainty in the estimation of density. Moreover, Fig.9a and Fig.9b shows that the match is very good and the residuals are small. The reliability of the inversion at the M well is verified.

4 Conclusion

As a global search algorithm, genetic algorithm is applied to the inversion calculation, which has the advantage of being free from constrain of the initial model. However, standard genetic algorithms often have premature convergence and non-convergence problems. Our new method can solve the problems. In the improved algorithm, the selection operator adopts regional equilibrium and elite retention strategy, which effectively prevents the algorithm from falling into local optimum and guarantees convergence. The crossover and mutation operators adopt adaptive probability to avoid slow convergence and more convergence. The simulation results show that our method has improved the prediction accuracy and has higher reliability than SGA. Meanwhile, it is a practical optimization tool with its effectiveness and performance advantages.