基于自适应粒子群的农机自动转向系统分数阶控制

张瑶,李佩娟，贾茜，刘树青

(南京工程学院工业中心，江苏 南京 211167)

农业智能化是现代农业发展的重要方向，智能农机转向控制系统可以提高作业效率，降低劳动强度.国内外多位学者在农机智能化控制方面作了大量的研究[1-5]，如贾全等[6]提出的自适应滑模控制方法，提高了拖拉机自动转向系统的可靠性；魏爽等[7]提出的农机自动导航路径搜索方法和基于预瞄点搜索的纯追踪模型，实现了农机的直线和曲线自动导航作业；王茂励等[8-9]设计了模糊PID方法，减小了超调，提高了转向精度.

分数阶PIλDμ控制器除了具有比例kp，积分kI，微分kd3个参数外，还有积分阶次λ和微分阶次μ两个参数[10-11]，设计灵活,控制性能优,能更好地调节被控系统的性能指标.因此，针对农机自动转向系统的控制问题，本文设计了分数阶PIλDμ控制方法，首先设计分数阶PIλDμ控制器，然后采用自适应粒子群算法对控制器的5个参数(kp，kI，kd，λ，μ)进行寻优，使得控制器能够快速且准确的找到参数，克服传统试凑法寻找参数的滞后性，提高农机自动转向系统的快速性和稳定性，为农机转向系统的发展提供了一种可靠的方法.

1 自动转向控制系统结构

农机自动转向控制系统由导航控制器、转向控制器、液压驱动系统、比例换向阀、农机转向系统以及转角测量模块几部分组成[12]，如图1所示.其工作原理为：由农机的导航控制系统计算出农机的目标转角后，通过总线将目标转角的值传递给下位机，转向控制器通过目标转向角和目前车轮的转角差值及转角差值变化率的不同，结合转向控制算法，控制液压驱动器来实时调节比例阀的方向和开度，完成农机自动转向功能，农机自动转向系统的传递函数表示为：

(1)

式中，R(s)是目标转角，c，d，e均为待定参数.

图1 自动转向控制系统结构图Figure 1 Schematic of automatic steering control

2 分数阶PIλDμ控制器设计

分数阶PIλDμ控制器是整数阶PDI控制器的拓展[13-14]，其传递函数可表示为：

G(s)=kp+kIs-λ+kdsμ

(2)

分数阶PIλDμ控制器具有积分阶次λ和微分阶次μ，利用各种智能算法对PIλDμ的5个参数(kp,ki,kd,λ,μ)进行优化，使得PIλDμ控制器具有更好的控制性能与效果.

利用Oustaloup滤波器算法，在有限的频域段(ωb，ωh)内，通过频域拟合的方法对微积分算子sα近似成整数阶传递函数的形式，算法如式(3)所示：

(3)

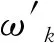
(4)

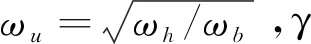
本文利用Simulink设计的分数阶PIλDμ控制器如图2所示.

图2 分数阶PIλDμ控制器Figure 2 Fractional-order PIλDμ controller

3 改进粒子群算法及参数优化步骤

3.1 基本粒子群算法

粒子群优化(partical swarm optimization-PSO)算法[15-16]是通过搜索当前最优值来寻找全局最优解，具体方法如下所述：

假设D维搜索空间中有N个微粒，设Xi=(xi1,xi2，…,xiD)为第i(i=1,2,3，…，N)个粒子的当前位置，Vi=(vi1,vi2，…，viD)为该粒子i的当前飞行速度，Pi=(pi1,pi2，…，piD)为粒子i所经历的最优位置，相应的适应值称为个体的最优解Pbest，整个粒子群搜到的最优位置为全局极值，gbest=(pg1,pg2,…,pgD).当找到这两个值时，根据公式(5)来更新粒子的速度与位置.

(5)

式中，i=1,2,…,N；c1,c2为非负学习因子，ω为非负的惯性因子.

为避免PSO算法容易早熟情况，对惯性因子采用非线性动态调整的方法，惯性权系数的变化公式：

(6)

式中，ωmax与ωmin分别表示ω的最大值和最小值，f表示当前粒子的目标函数值，fmax表示所有粒子的平均值，fmin表示粒子的最小值.

适应度函数选取是粒子群算法进行优化的主要依据，适应度函数ITAE如下：

(7)

式中，e(t)为控制误差，J越小，表示粒子代表的参数性能越好.

3.2 自适应粒子群算法及参数优化步骤

自适应粒子群算法是一种根据粒子聚集程度智能调节粒子的算法[17-20]，需要引入交叉与变异操作，引入这些操作的概率为：

P=α+Geβ

(8)

式中，α和β是概率调整系数，Ge是指粒子的最优值无变动或者变动很小的代数累计值.具体调节流程如下：

备份全局最优粒子，计算种群中每个粒子与种群最优粒子的空间距离，若计算得到的值小于设置的阈值，说明种群粒子过于聚集，为了防止算法过早收敛，引入交叉操作，加强对该粒子和种群最优粒子之间的空间区域的搜索.两个粒子的空间距离定义为：

(9)

式中，x1和x2表示群中的两个粒子，D为粒子维数.阈值为：

Δφ=|iter/itermax-1|n×(ub-lb)

(10)

iter与itermax分别表示算法现在和最大迭代次数，ub与lb分别表示群中粒子位置的上下限，n是调节参数.由(10)式可知，阈值随着粒子群的不断更新而减小.为了防止算法因早熟而结束迭代，需要增大阈值，所以增大交叉和变异的粒子数量，粒子的交叉方式如下：

(11)

x1与x2是上代粒子，经过交叉得到cx1与cx2，e是一个介于(0,1)之间的D维随机数列.计算并得到新粒子的适应度，若优于原来的粒子，则对粒子进行更新，否则，对粒子进行变异，加强对粒子周边区域的搜索，变异方式如下：

(12)

式中，mx1与mx2为变异的粒子，γ为变异权值.

具体算法实现步骤如下：

步骤1)：初始化算法的各种参数，随机生成一个粒子群；

步骤2)：根据式(7)计算各个粒子的适应度，并根据适应度值选择种群粒子个体最优值和全局最优值；

步骤3)：根据(8)式计算种群的调整概率P，如果P≻Pm，Pm∈(0，1)，则执行步骤4，否则执行步骤7；

步骤4)：备份种群最优粒子，根据条件对粒子进行交叉，变异操作；

步骤5)：对种群最优粒子在周边区域值进行微小调整，计算并得到新的适应值，选择个体最优粒子代替种群最优粒子；

步骤6)：再次计算种群粒子适应度值，更换适应度差的粒子；

步骤7)：按式(5)更新粒子的位置与速度；

步骤8)：如果模型性能指标达到控制要求，退出，反之，返回步骤3.

4 仿真实验

文章采用文献[12] 雷沃TA800农机试验平台，该农机的系统结构和图1的结构一致，转向系统的传递函数为

(13)

利用Simulink搭建农机转向系统分数阶PIλDμ控制器模型，如图3所示.优化算法中的粒子为5维，各维分别为(k1,kp,kd,λ,μ)，c1=c2=2，权值ωmax=0.8,ωmin=0.6，最小适应值为0.01，优化过程中最大迭代次数为30，粒子群规模为20，kp,kI,kd的范围设置在0～500之间，取整数，λ，μ设置在0～1之间，经过优化后，kp=95，ki=450,kd=

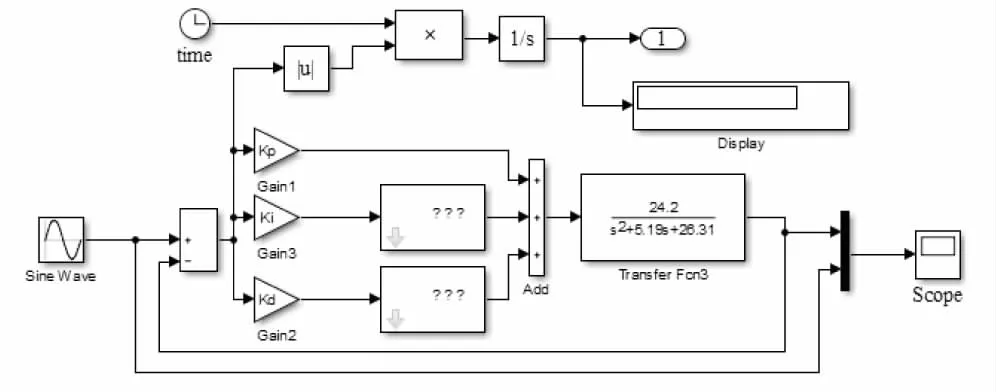
图3 农机转向系统分数阶PIλDμ控制模型Figure 3 The fractional order simulation model of agricultural machinery steering system

20，λ=0.975 3，μ=0.998 4，分数阶PIλDμ控制器为

(14)

图4是适应值的计算过程，图5和图6是5个参数(kp，ki，kd，λ，μ)的优化曲线，由图4～6可以看出，大约在迭代5次左右模型基本达到稳定，满足了控制系统快速性及稳定性的要求.图7是农机转向系统的阶跃响应，模型大约在t=0.01s到达稳定状态，稳态误差为零，传统PID控制方法大约在t=1s才到达稳定状态，且超调量大，故分数阶PIλDμ控制器的控制效果优于传统PID控制方法，其中传统PID控制器的3个参数(kp，ki，kd)来自文献[12]，阶跃响应的具体性能指标见表1.

为了进一步验证模型的准确性，让模型跟踪正弦信号和随机信号，效果如图8和图9所示.由图8～9可知，分数阶PIλDμ控制方法能够较好的跟踪预先给定的信号，跟踪效果较好，能够实现农机转向系统的精确控制.

图4 进化代数与适应值关系Figure 4 Relationship between evolutionary algebra and fitness

图5 参数优化曲线1Figure 5 Parametric optimization curve 1

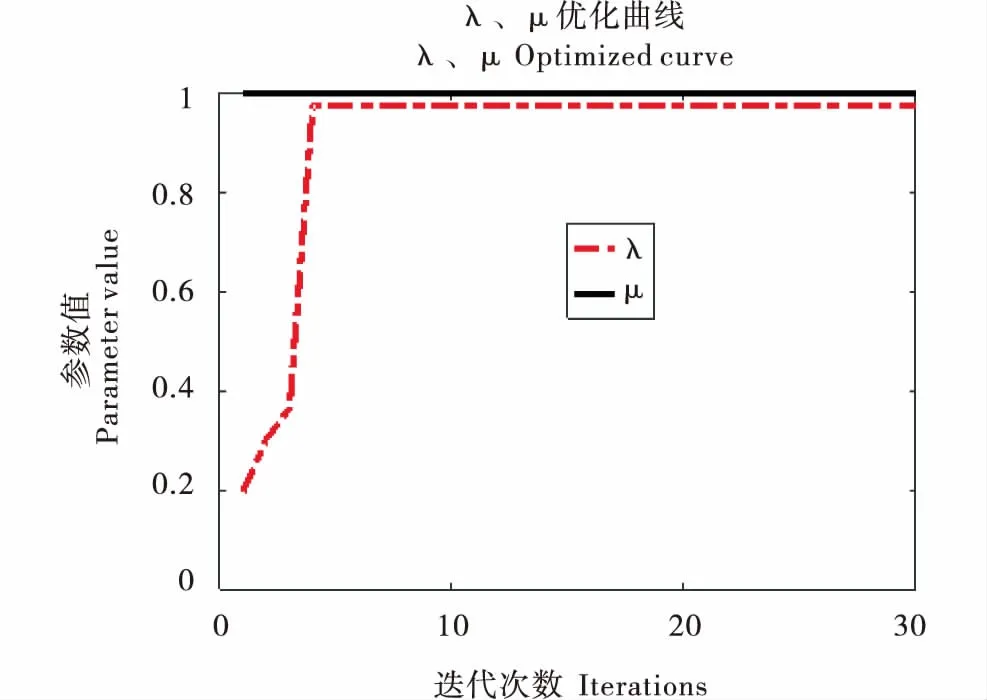
图6 参数优化曲线2Figure 6 Parametric optimization curve 2

参数Parameter传统PIDTraditional PID分数阶PIDFraction oder PIDkp4.495ki17.4450kd0.520λ/0.957 3μ/0.998 4上升时间/(t·s-1)Rising time0.250.0125超调量/%Overshoot190.01稳态误差/%Steadystate error0.010

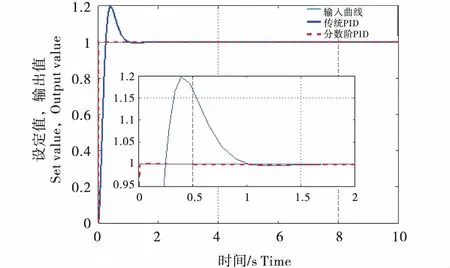
图7 阶跃信号跟踪实验Figure 7 Step signal tracking experiment

为了验证模型的鲁棒性及模拟田间的一些复杂的环境因素，在4s时给转向系统加幅值为0.5，时间为1s的阶跃信号，如图9所示，模型具有较强的抗干扰能力.

图8 正弦信号跟踪实验Figure 8 Sinusoidal signal tracking experiment

图9 随机信号跟踪实验Figure 9 Random signal tracking experiments

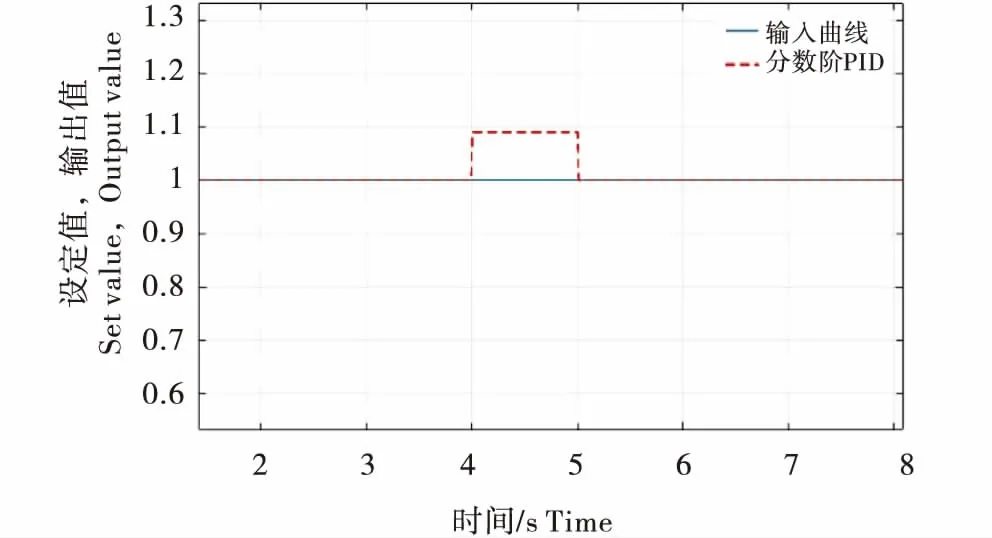
图10 抗扰动实验Figure 10 The disturbance diagram

5 结论

针对电控液压式农机转向系统的不稳定及响应慢等特点，提出一种分数阶PIλDμ控制器控制农机自动转向系统的方法，其中采用自适应粒子群算法对控制器的5个参数(kp,kI,kd,λ,μ)进行寻优，阶跃响应的仿真结果表明，系统的上升时间小于传统PID控制方法，几乎无超调量和误差，并且对干扰信号有良好的抑制作用，其他两种信号的跟踪效果也较好，该方法对农机转向系统的稳定性及控制精度具有重要的意义.