基于模糊函数的MIMO雷达跳频相位编码波形设计

刘锦 杨德贵 梁步阁 朱政亮 赵锐

( 中南大学航空航天学院， 长沙 410083)

与传统相控阵雷达相比，MIMO雷达的特性具有多种优势：(1) 通过发射正交波形，在发射端形成低增益的宽波束，降低了雷达的截获概率；(2) 照射面积广，便于进行多目标跟踪；(3) 通过对正交信号回波的处理，可得到比发射阵元数目更多的观测通道；(4) 抑制目标闪烁问题。这些特性的实现和波形的正交性密切相关，正交波形设计是MIMO雷达系统设计中至关重要的部分[1-3]。

除线性调频信号外，MIMO雷达发射的其他信号都可以视为由多个子脉冲组成，各个子脉冲间以一定间隔组成脉冲串，或前后无间隔相连组成大脉冲信号予以发射。通过对各子脉冲信号的频率、相位、时宽进行编码来实现正交[4]，相位编码和频率编码是最常用的正交编码方式。国内外学者针对这两种编码方式，特别是在其优化算法方面作了较多研究，但是将两者结合起来的研究较少。文献[5]中从发射方向图的角度，研究了正交频分相位编码信号(OFD-PC)。文献[6]中通过混沌系统来生成频率相位编码信号。大多数研究采用的是单一编码方式中常用的自相关函数及互相关函数的一次、二次组合，而基于模糊函数优化准则、目标函数方面的研究很少。因此，我们希望展开对跳频相位编码信号的模糊函数推导研究。

本次研究中，引入文献[7]中MIMO雷达收发模型的思路，对跳频相位编码信号的模糊函数进行推导，并进行仿真验证和分析。正交波形设计可分为目标函数设计部分和序列最优化设计部分，本次设计即包括这两部分。目标函数设计决定了对波形特性的需求，而最优化设计则决定了运算的效率以及波形的性能精度。

1 基于模糊函数的MIMO雷达多参数目标函数推导

目前，MIMO雷达的评价准则主要有模糊函数、发射放线图、信噪比、信息和估计理论等准则。其中，模糊函数是衡量雷达系统分辨率性能的重要工具，它反映了系统对距离-多普勒域相邻目标的分辨能力[8]，在信号检测、参数估计、波形设计、性能评估等方面得到了广泛应用。模糊函数的本质就是信号经过匹配滤波后的输出，因此，我们先从MIMO雷达收发模型开始进行分析。

假设MIMO雷达为M发N收，并且其发射和接收天线为线阵排列的简单形式。在图 1所示MIMO雷达收发模型中，M个发射天线和N个接收天线在同一条直线上。 将第m个发射天线位置记为xtm，第n个接受天线位置记为xrn，第i个天线发射的信号记为ui(t)。

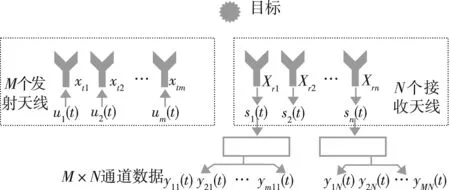
图1 MIMO雷达收发模型

在一个点目标下，点目标到发射天线的距离为τ·c2，多普勒频率影响为ν，发射天线位置的影响对应归一化空间频率fs[7]，记作(τ,ν,fs)。可以将第n个天线目标响应记作：

(1)

其中，um(t)为第m个发射天线的发射信号。根据N个接收天线收到信号后匹配滤波器的输出，定义模糊函数：

(2)

当(τ,ν,fs)=(τ′,ν′,fs′)时，发射信号和滤波器完全匹配，输出的信号信噪比最大；否则，会产生失配现象。代入信号，得到：

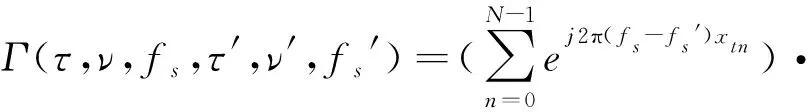
(3)

其中，第一部分包含接收天线的位置信息，但和雷达的发射信号um(t)无关。 第二部分包含um(t)、发射天线的位置、时延、多普勒频率、归一化空间频率，对系统的距离及其多普勒性能有影响。因此，研究主要集中在第二部分，将其定义为MIMO雷达模糊函数：

(4)

在此模糊函数的基础上，代入不同的发射波形将得到不同的目标函数，以最小化次函数进行优化设计就可以得到相应的波形。而且，若将其中求和项中与t有关的项提出来，即

这部分就是发射信号的相关函数。当m=m′时为自相关，当m≠m′时为互相关。本次研究的模糊函数在考虑了相关函数的情况下综合了发射天线的位置信息。针对跳频相位编码信号进行设计，跳频编码信号如式(5)：

(5)

由于实际实现时有一定的复杂度，带宽和持续时间一般都较小，其信号属于多普勒敏感信号，无法测量速度过大的物体。νTp很小，ej2πνt可视为实数1。代入跳频相位编码信号，可得式(6)和式(7)：

(6)

χrect(τ-(q′-q)Δt,(cmq-cm′q′)Δf)

(7)

可以看出，式(6)中第二项只与信号的脉宽有关，而与信号的具体调制信息无关，因此目标函数定义如式(8)：

χrect(τ-(q′-q)Δt,(cmq-cm′q′)Δf)

(8)

其中：

χrect(τ,ν)1[0,Δt)(t)·1[0,Δt)(t+τ)ej2πνtdt

(9)

可以看出式(8)中第一项ej(φq-φq′)与载波相位有关，第二项e-j2πcm′q′Δfτ与载波频率调制有关，第三项ej2π(cmq-cm′q′)qΔt与发射天线位置有关。若令cmq=cm′q′=1，则相位频率编码信号退化为相位编码信号，模糊函数退化为相位编码模糊函数；若令φq=φq′=0，则相位频率编码信号退化为调频编码信号，模糊函数退化为调频编码信号模糊函数。可以对相位频率按式(10)(11)进行单独优化和联合优化。

(10)

χrect(τ-(q′-q)Δt,(cmq-cm′q′)Δf)·

(11)

2 基于遗传算法的优化设计

确定目标函数后，选择适当的优化算法对序列{φmq、cmq}进行优化设计。针对这种编码位较多的组合优化问题，现有的应用算法主要有蒙特卡洛算法、遗传算法、模拟退火算法、粒子群算法等。有研究表明，对于参数较多的组合优化问题，精确求解全局最优解的方法是不存在的。一般只能获得搜索空间内的最优解，而优化算法可以在一定程度上加快搜索速度，缩短达到同一精度要求所耗费的时间；甚至，对优化算法的局部收敛问题进行优化，得到更大搜索范围内的最优解，但这往往要耗费更多的计算时间。本次研究中，通过大量仿真实验统计，采用经典的200代遗传算法将时间优化为100～200 s。若对精度要求降低，并把迭代次数降为50代，运算时间可略微缩短，但仍在10 s量级，无法实现实时优化，离实际应用要求有较大差距。因此，我们的工作侧重于对目标函数的推导和仿真波形性能的分析，只选用最经典的遗传算法来进行优化设计。遗传算法框图如图2所示。

图2 遗传算法框图

在SIMO雷达中，理想的模糊函数为图钉状。由式(8)可以看出，MIMO雷达的模糊函数在Ω(0,fs,fs)处达到峰值。为了使函数的波峰尽量陡峭，将代价函数fp(C)定义为峰值的陡峭程度，用Ω(τ,fs,fs′)的p阶来表示，优化时只需尽量使其最小：

(12)

3 仿真实验与结果分析

采用4发4收MIMO雷达，天线以等间距线阵的简单方式排列，发射位置坐标分别为(-3,0)、(-1,0)、(1,0)、(3,0)，遗传算法设置参照以上参数。

3.1 有效性验证

将式中cmq=cm′q′=1，子脉冲个数为40的相位编码信号，采用4相位编码。种群经过遗传迭代优化后选取最优解，得到相位编码序列(见表1)。

正交信号的自相关和互相关特性，直接决定了MIMO雷达的目标检测性能。通常，在不考虑位置信息和其他复杂条件的情况下，为了降低虚警和弱小目标被掩盖的漏警概率，要求发射信号具有较低的自相关旁瓣。为了保证不同天线发射信号之间的有效分离，要求发射信号具有较低的互相关旁瓣。表2中主对角线上数值为最大自相关旁瓣(ASP值)，非主对角线数值为最大互相关(CP值)。表3所示为本研究方法和文献[9]方法的ASP及CP参数对比。由表2可以看出，运用本方法设计的正交波形自相关函数没有明显的高旁瓣，自相关、互相关旁瓣电平都较低，具有较好的自、互相关性能。由表3可以看出，本次研究的平均ASP为0.290 1，平均CP为0.261 6，已达到和文献[9]相当的水平。这就验证了本方法的有效性。

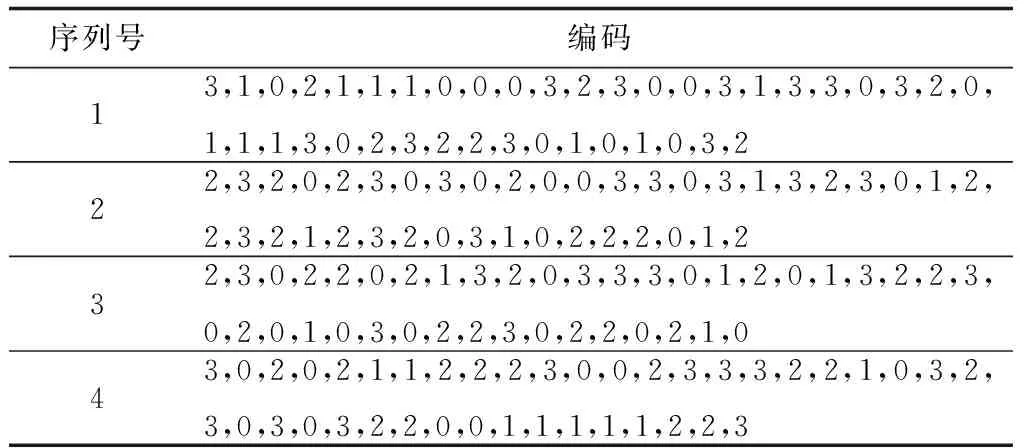
表1 N=40,L=4,M=4的相位编码信号优化序列

表2 正交四相码的ASP和CP

注：带“*”数据为主对角线上的4个ASP值，其余数据为CP值

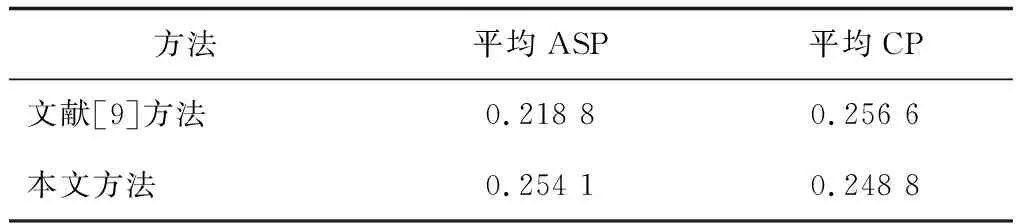
表3 两种方法的平均ASP及平均CP

当然，文献[10]中对优化算法作了进一步优化，并组成组合算法，以自相关、互相关函数为适应度函数，可以对优化结果进一步完善，得到自相关性、互相关性更优的优化序列。

3.2 相关特性优化分析

跳频编码或相位编码信号能获得较好的自相关和互相关特性，但是单一的编码方式中编码数量有限，而且正交性受单一体制的固有影响，因此，将跳频和相位结合起来可以获得更大的编码选择空间，并且其正交性也会得到进一步改善。

本次研究是在跳频编码的基础上加入相位编码，获得跳频相位编码信号，如图3所示。图3中，a 图是文献[7]跳频编码信号；b图是本次加入相位的跳频相位编码信号，其中有部分区域信号幅值为固定电平。因为图中表示的都是基带信号，调制到载频上幅值电平则体现为调制信号的初相位。

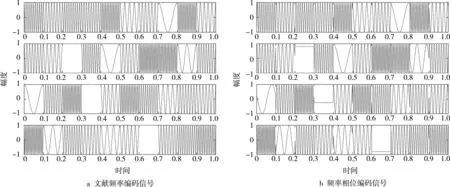
图3 频率相位编码基带信号时域图

跳频相位编码、单一相位编码、跳频编码信号的适应度函数、相关函数特性如图4所示。图4中，a图分别选用相码为4、8、32、128时的优化效果，纵坐标为适应度函数的幅度。可以看出，以本次研究的适应度函数为标准，跳频相位编码信号的优化效果相对相位编码，适应度降低了0.6，相对频率编码信号降低了0.01。这是因为单一跳频编码信号的适应度优于相位编码信号。本研究的目标函数能同时对相位、跳频、跳频相位编码信号进行分析。b图、c图、d图分别为单一相位编码、跳频编码、跳频相位编码信号的相关特性图，其相关函数如式所示。跳频相位编码信号相关函数比b图中的相位编码信号降低了10～20 dB，比c图中的跳频编码信号降低了0.5 dB。这说明跳频相位编码信号融合了两者的优点，对两种单一信号的正交性都有一定改善。

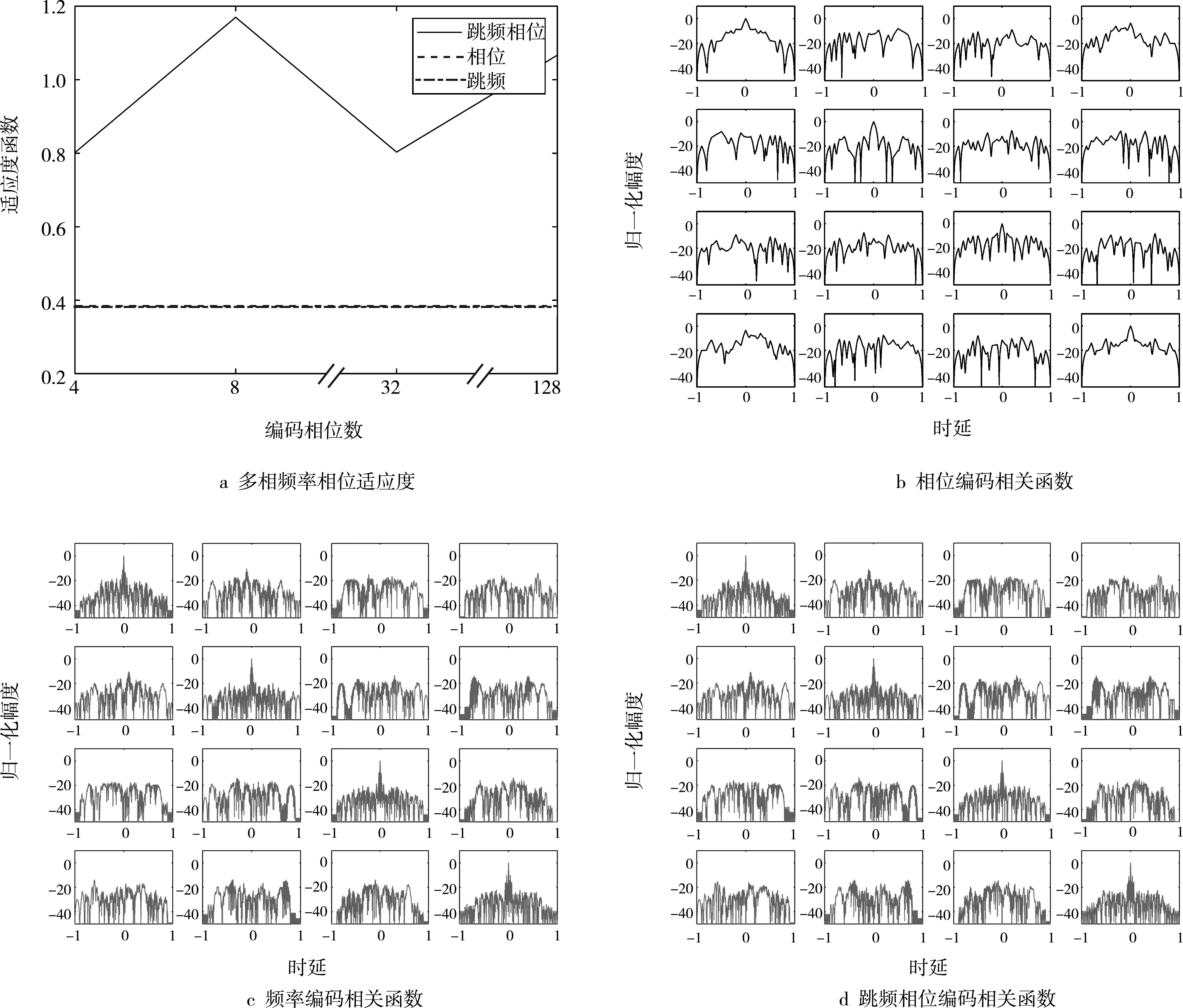
图4 跳频相位编码目标函数及相关函数改善图

文中采用了多次不同的结合位置信息进行分析，发射天线间距分别为1、2、5 m，其余参数相同，然后用遗传算法进行优化，其仿真结果如表4所示。对这一个适应度函数最小的序列，根据不同发射天线计算其相应的适应度，如表5所示。

可以看出,当天线位置从1 m到5 m逐渐加大时，适应度函数的值也相应地增大，尽管其差别较小。这也说明了在考虑到发射天线位置、目标多普勒频率和归一化空间频率时，发射天线间距越远，同一组发射波形的匹配滤波器的输出在缓慢变弱，虽然变化可能比较细微。

表4 正交32相码波形序列

表5 天线位置间距与适应度函数关系

究其原因，是因为随着发射天线距离的增加，目标的多普勒频率、归一化空间频率的相对差异在变大。在图5所示目标多普勒频率影响模型中，考虑了模型的简化。当两个天线的距离加大时，其信号受到目标运动速度带来的多普勒频率的影响的差异变大，对信号的正交性相应会造成微弱的影响。同时，其归一化空间频率同理，在适应度上的反映如表5所示。

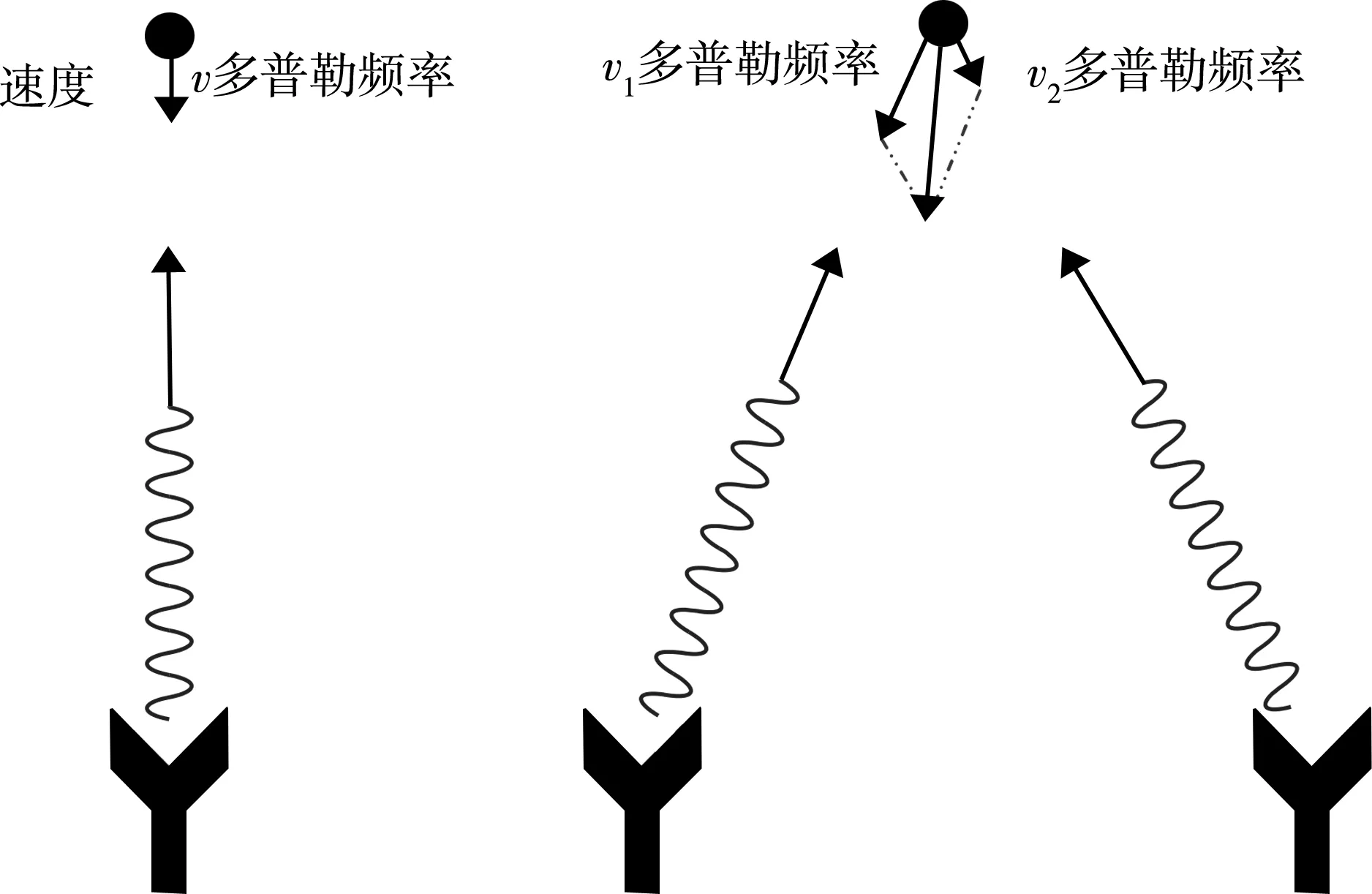
图5 目标多普勒频率影响模型

4 结 语

在本次研究中，针对MIMO雷达跳频相位编码信号，综合考虑了信号参数(频率及相位)、天线位置等多参数信息，基于模糊函数推导了正交波形设计的目标函数。同时，采用遗传算法进行优化设计，得到一组具有良好自相关和互相关特性的波形,验证了目标函数设计的有效性，并对跳频相位编码信号、单一跳频编码、相位编码信号的正交性进行了对比。

仿真结果表明，基于本次推导的目标函数的MIMO雷达正交波形不仅具有良好的正交性，还可提供天线位置等参数。跳频相位编码信号继承了跳频编码与相位编码的优点，正交性比单一跳频、相位编码信号要好。通过仿真结果发现，当天线位置不同时，匹配滤波器的输出会有细微的变化。在一定范围内，随着天线间距加大，发射波形受多普勒频率及归一化空间频率的影响而发生变化，推导的目标函数值会有所降低。

本次推导的评价函数针对的是跳频相位编码信号，不适用于时空等更复杂的波形。在算法优化方面，可以对遗传算法予以改进，加快其收敛速度和精度。