考虑渗透率时变的深部调驱技术数值模拟研究

李彦来 孙召勃 马奎前 姜瑞忠 花靖

(1. 中海石油(中国)有限公司天津分公司， 天津 300459； 2. 中国石油大学(华东)， 山东 青岛 266580)

老油田高含水期取心资料和矿场测井资料显示，由于注入水的长期冲刷，油藏的渗透率发生了很大的变化。在中高渗透油藏，地层渗透率明显增加，地层中形成了一些大孔道和高渗透条带，注入水沿高渗透条带突进，使油井过早见水或暴性水淹，水驱开发效果较差[1-2]。随着油田进入高含水、特高含水开发期，传统的小半径调剖作业已经不能满足其开发要求。具体表现在，注入井近井地带含油饱和度已经大大降低，不具备调剖价值；浅堵浅调只能使注入水在近井地带转向，而进入油层深部后，注入水发生绕流进入高渗透条带，无法起到稳油控水的作用。深部调驱技术是在传统调剖堵水技术上发展起来的新技术，应用越来越广泛。应用该技术，能够在地层深部针对大孔道实现调剖和驱油。

1 深部调驱数值模拟技术研究现状

堵水调剖剂种类繁多，根据调剖机理可以将其归纳为凝胶类深部调剖剂、微生物类深部调剖剂、沉淀性无机盐类深部调剖剂等类型[3-6]。

研究者在调剖调驱机理和数值模拟等方面作了多项研究。1990年，Gao 等人编制了三维三相交联聚合物调驱模拟器[7]。1992年，Sorbie等人通过实验和数值模拟研究了黏性窜流对非均质多层油藏调驱效果的影响[8]。2002年，Delshad Mojdeh等人编制了能够模拟复杂化学驱(聚合物驱、凝胶调驱等)的数值模拟器[9]。2005年，冯其红等人建立了考虑毛管力和重力的两相多组分三维流线可动凝胶深部调驱数学模型[10]。2006年，吴行才等人通过实验研究发现，可动凝胶在渗流过程中表现出非线性特征[11]。2011年田鑫等人引入了描述微凝胶突破运移的启动压力梯度，建立了三维两相三组分的可动微凝胶调驱数学模型[12]。

在各类数值模拟器中，ELCLIPS-E200、VIP-POLYMER等商业模拟器可以用于多组分隐式求解，但其机理极为简单，不能表征调驱物化反应。FAPMS、UTCHEM、CMG等商业数值模拟器可以描述调驱物化反应，简化物化机理的表征方法。一些特殊特征无法通过上述模拟器进行表征，比如深部调剖的机理表征。

此外，当油藏进入高含水期后，在长期冲刷作用的影响下，储层的性质会发生较大变化(主要表现为渗透率和相渗曲线的变化)，从而对深部调驱决策过程产生影响[13-15]。

总体上，目前通用的数值模拟软件对深部调驱机理的描述比较单一，远远跟不上矿场应用调驱体系的发展；同时，这些数模软件没有将注入水冲刷造成的储层渗透率时变现象考虑进去，不能准确地描述油藏开发特征。本次研究中，在一种新型深部调驱体系(核壳聚凝体系)的基础上，将储层渗透率时变这一因素考虑进去，建立深部调驱的三维三相六组分数学模型，并运用数值模拟软件对影响深部调驱效果的参数进行分析。该数学模型主要针对核壳聚凝体系，其封堵机理与阴阳离子聚合物深部调剖剂相类似，模型也适用于原理相近的其他堵剂。

2 深部调驱数值模拟技术的实现方法

2.1 时变表征方法

首先，定义无因次变量 —— 岩心孔隙体积冲刷倍数，表征其对储层渗透率的影响；然后，建立式(1)所示二者之间的数学关系，从而实现对渗透率时变的定量表征。

Rwpv=∑QwVporv

(1)

式中：Rwpv—— 孔隙体积冲刷倍数，无因次；

Qw—— 注入水流量，m3；

Vporv—— 孔隙体积，m3。

根据式(1) 计算出网格孔隙体积冲刷倍数Rwpv，将黑油模型(Black Oil Model)中的K(P) 重新定义为K(P，Rwpv) ，即可考虑储层渗透率时变现象。

2.2 核壳聚凝体系物化机理表征方法

2.2.1 体系黏度

黏度是深部调驱体系的一项重要参数，核壳聚凝体系的黏度主要取决于悬浮分散剂组分的浓度。在零剪切情况下，悬浮分散剂浓度越大，体系黏度也越大。采用输入表格的方式，输入体系中的静态黏度与质量浓度关系。对于体系流变性的处理，一种是采用Meter公式计算，另一种是使用表格的方式输入并进行插值计算。

(2)

μapp=μw[1+(P-1 )M]

(3)

式中：μw—— 水相黏度，mPa·s；

μ0x——零剪切条件下悬浮分散剂的体系黏度，mPa·s；

μapp—— 悬浮分散剂体系视黏度，mPa·s；

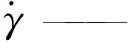
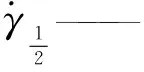
fpown—— 由实验资料确定的常数；

P—— 悬浮分散剂体系对水的增黏倍数，无因次；

M—— 剪切作用对体系黏度的削弱倍数，无因次。

2.2.2 组分吸附

当体系溶液流经多孔介质时，悬浮分散剂和聚凝剂会被岩石表面吸附。此过程可以视为不可逆吸附，满足Langmuir(朗缪尔)吸附公式：

(4)

式中：a、b—— 实验测得常数；

Ci—— i组分的质量浓度，kgm3；

cadi—— 单位质量岩石对i组分的吸附量，kg。

2.2.3 可及孔隙体积

由于受孔隙大小、孔喉半径等的影响，悬浮分散剂和核壳体只能进入较大的孔隙空间。用φa表示悬浮分散剂和核壳体混合物能够进入孔隙体积的分数，其值通过实验来确定。

2.2.4 体系反应

核壳聚凝体系在地层中的反应较复杂，在此对其作以下简化设定：组分间存在反应配比和门限质量浓度；核壳发生反应后完全进入生成物中；反应生成物不流动，不单独视为一个组分。

2.2.5 渗透率下降作用

渗透率下降主要体现在2个方面：一是核壳聚凝体系在多孔介质中的吸附滞留引起地层渗透率下降，用残余阻力系数(RFF)表征；二是反应产物对地层渗透率的影响，用渗透率下降系数(Rk)表征。两者以表格方式输入并进行插值计算。

2.3 建立数学模型

2.3.1 模型假设

在建立数学模型时首先作如下基本假设：油藏等温；流体的流动过程符合达西渗流定律；油藏中物化反应瞬时平衡；油藏岩石和流体可微压缩；模型包括油气水悬浮分散剂核壳体聚凝剂的6个组分，除油气组分外，其余组分均在水相中。

2.3.2 模型方程

根据基本假设和物质守恒原理，推导出油气水地下渗流和化学剂组分的基本微分方程。

(1) 油组分方程：

(5)

(2) 气组分方向：

(6)

(3) 水组分：

(7)

(4) 悬浮分散剂组分：

(8)

(5) 核壳体组分：

(9)

(6) 聚凝剂组分：

(10)

式中：Va—— 可及孔隙体积，小数；

RFF—— 残余阻力系数，通过实验确定；

Rk—— 渗透率下降系数，通过实验确定；

K—— 绝对渗透率，10-3μm2；

Krl—— l相相对渗透率，l相分为o(油)、g(气)、w(水)相；

Bl—— l相体积系数；

μl—— l相黏度，mPa·s；

pl—— l相压力，MPa；

γl—— l相重度，Nm3；

Sl—— l相饱和度，小数；

qi—— i组分源汇项；

D—— 深度，m；

φ—— 孔隙度，小数；

ρr—— 岩石密度，kgm3；

Rs—— 溶解气油比(体积比)。

2.3.3 辅助方程

饱和度方程：

So+Sw+Sg=1

(11)

毛管力方程：

pcog=pg-po

(12)

pcow=po-pw

(13)

式中：pcow—— 油水界面张力，N；

pcog—— 油界面张力，N。

3 软件设计

3.1 模型解法及软件编制

对上述建立的数学模型进行差分离散，得到数值模型，按照如下步骤求解：

(1) 采用全隐式方法求解气、油、水的压力和饱和度场。

(2) 分别计算每个网格的冲刷孔隙体积倍数。

(3) 采用算子分裂法求解饱和度场，将浓度方程分为对流方程和扩散方程，分别用隐式迎风格式和追赶法进行求解。

(4) 根据模型储层和流体物性与网格孔隙体积冲刷倍数的关系，计算新的网格渗透率、相对渗透率、毛管力及原油黏度，并更新网格相应参数。

(5) 利用计算得到的浓度场，计算化学剂反应、吸附、离子交换的量，以及化学剂对流体黏度、毛管压力和相渗的影响，再次更新网格相应的参数。

(6) 对应每个时间步，重复上述所有步骤，直到模拟结束。

针对模型，我们编制了一体化数值模拟软件，软件具有较好的前处理、后处理功能。其中核心计算部分采用 FORTRAN90 语言进行编写，视窗界面采用 Visual C#进行设计。

3.2 深部调驱机理在数值模拟中的体现

建立五点井网概念模型(网格数为10×10×3；X=Y=20 m；DZ=5 m；正韵律)，利用编制的深部调驱数值模拟器，对深部调驱体系机理进行研究。分别建立考虑了储层渗透率时变的水驱和深部调驱2套方案，对比其模拟结果。

分析含油饱和度与生成物阻力系数平面分布图(见图1)可知，与水驱相比，储层平面上，实施深部调驱后，调驱体系封堵了高渗透条带，使注入水发生绕流现象，扩大了水驱波及范围，提高了油藏的动用程度，开发效果变好。由生成物阻力系数分布图可知，调驱体系生成物所在的部位就是注入水发生绕流的部位。

分析图2可知，纵向上与水驱相比，调驱体系首先进入高渗层，在储层深部发生反应以封堵高渗透层，使得高渗透层的水绕流至上部中低渗透层，改善了层间吸水剖面，增加了注入水波及范围，开发效果变好。根据含油饱和度与生成物阻力系数纵向分布图，判断出调驱生成物所在的部位就是注入水发生绕流的部位。

根据以上分析，认为该深部调驱体系可以在储层深部封堵高渗透条带和高渗透层，使液流转向，提高注入水波及范围。

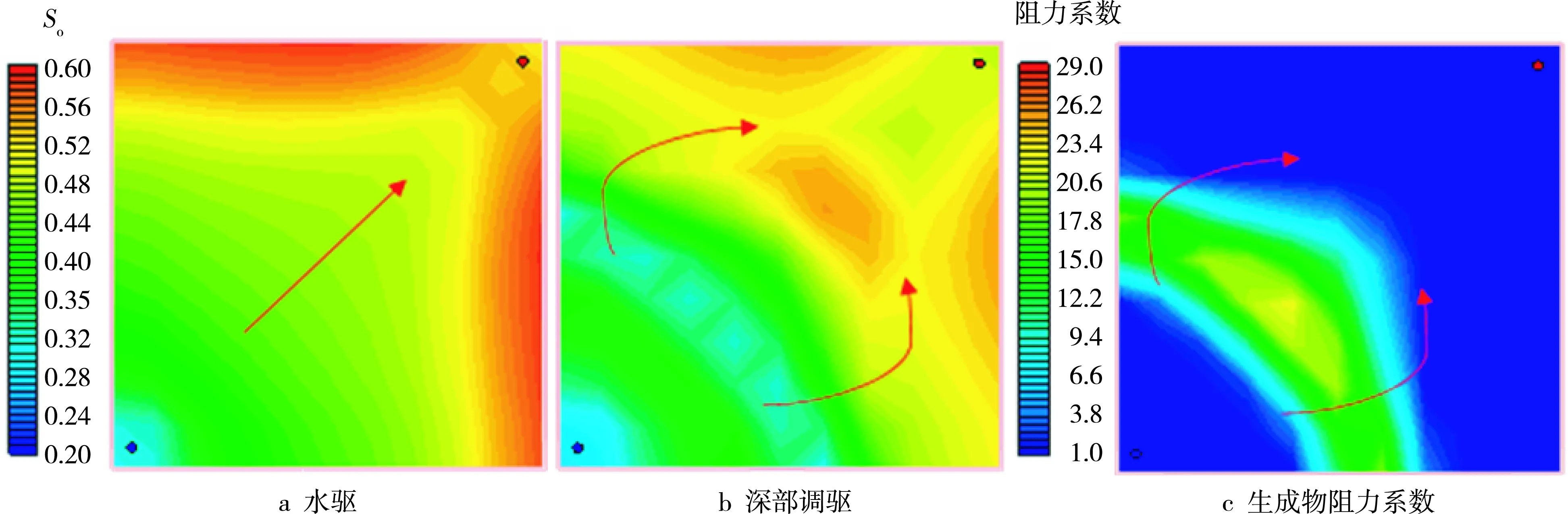
图1 含油饱和度与生成物阻力系数平面分布图

图2 含油饱和度与生成物阻力系数纵向分布图

根据渗透率分布对比图(见图3)分析可知，渗透率时变对储层渗透率的分布有显著影响，注入水长期冲刷会使地层形成一些高渗透条带和大孔道，导致储层非均质性增强，注入水利用率低，开发效果差。

通过以上论述可知，所编制的深部调驱一体化数模软件可以很好地刻画储层深部调驱机理，也可以描述储层渗透率时变现象。本软件可以用于指导矿场生产。

4 深部调驱数值模拟应用分析

从S油田大模型中选取试验区进行整体深部调驱优化设计，模型划分为62×60×17个网格，各油层之间存在隔层，不考虑注入水层间窜流。通过模拟，预测该试验区未来15年间水驱、深部调驱的开采指标，以指导油田后续开发。

分析S油田含油饱和度与生成物阻力系数平面分布图(见图4)可知，与水驱相比，实施深部调驱后，调驱体系生成物封堵了储层高渗透条带，使注入水发生绕流，扩大了水驱波及范围，改善了油藏开发效果。

S油田生产指标预测图(见图5)显示，与水驱相比，试验区实施深部调驱后，含水率下降，采出程度升高，开发效果变好。这是由于水驱过程中，油藏存在非均质性，渗透率时变效应使得储层非均质性得到增强，而实施深部调驱后，体系生成物封堵了部分高渗透条带，迫使注入水发生绕流，增加了波及范围，采出程度提高。

与水驱相比，试验区实施深部调驱后预计累计增油25 332 t，提高采出程度1.25%，效果显著。

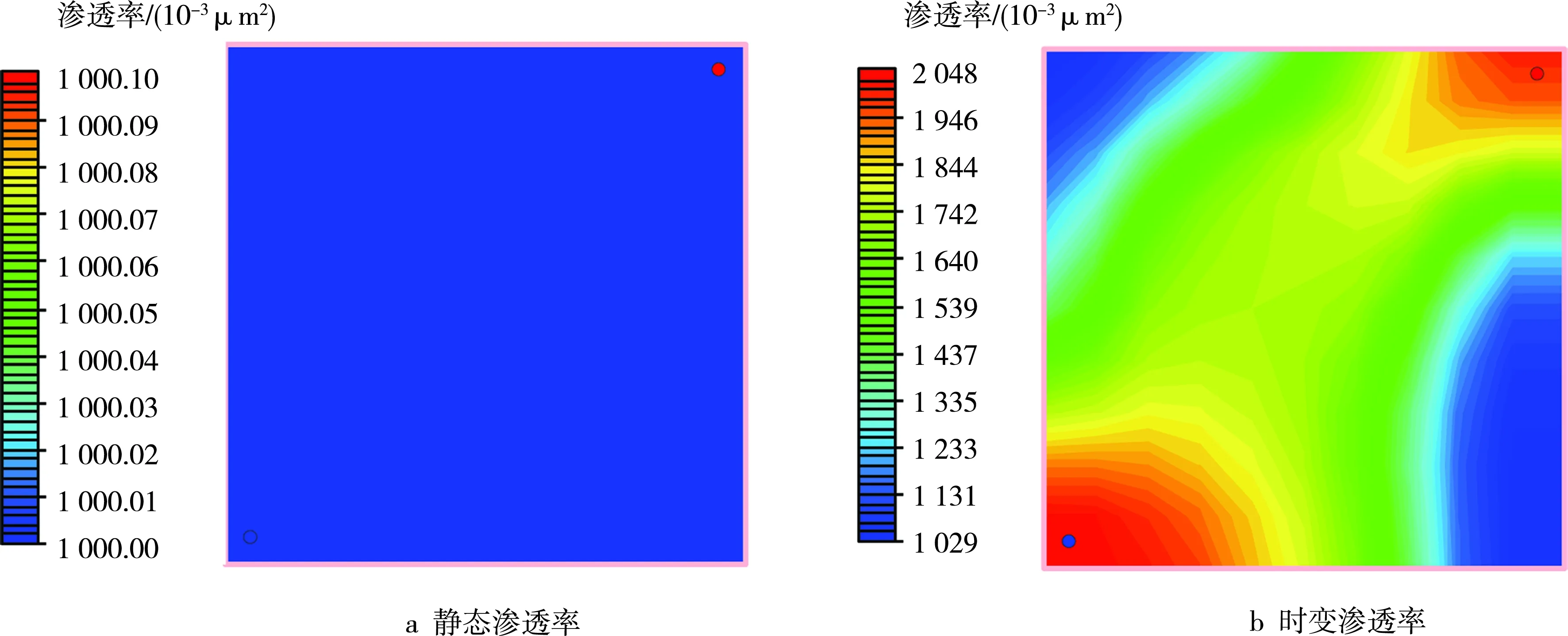
图3 渗透率分布对比图

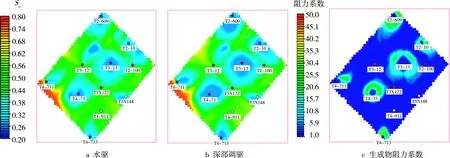
图4 S油田含油饱和度与生成物阻力系数平面分布图

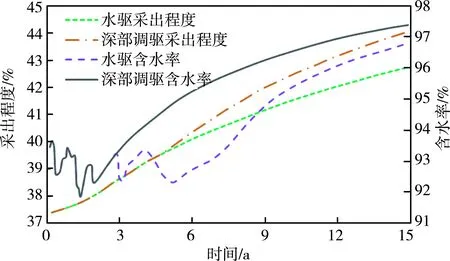
图5 S油田生产指标预测图

5 结 论

(1) 储层渗透率时变会增加储层非均质性，使注入水利用率低，水驱开发效果差，因此在油田开发过程中应考虑这一机理。

(2) 分析渗透率时变现象的原理，建立了相应的数学模型，并编制了深部调驱的数模模拟器，指导深部调驱决策。

(3) 编制的数模软件可以很好地刻画深部调驱封堵机理。模型显示，深部调驱体系可以封堵储层深部的高渗透条带、大孔道和高渗透层，使得注入水发生绕流，增大波及范围，起到稳油控水的作用。

(4) 编制数值模拟一体化软件，对S油田进行了深部调驱数值模拟研究。采用深部调驱方案后，累计增油量25 332 t，提高采出程度1.25%，效果显著。