基于信赖域算法的试井曲线自动拟合研究
2019-09-18王一陈殿远韩鑫郑志锋张骞
王一 陈殿远 韩鑫 郑志锋 张骞
(中海石油(中国)有限公司湛江分公司, 广东 湛江 524057)
试井自动拟合分析算法本质上是一个解决地层或油藏未知参数的非线性函数问题,即采用试井分析理论模型去匹配实际测试的压力数据,从而求解最佳地层参数。国内外学者一般是将通过试井解释求解地层参数的问题转化为非线性最小二乘法问题[1-2]。对于非线性最小二乘法问题的求解,目前一般采用Newton算法(牛顿算法)和Gauss - Newton法(高斯-牛顿算法)[3-6]。同时,在此基础上不断优化并发展了一些新算法,如Levenberg-Marquardt算法(莱文贝格-马夸特算法,简称LM算法)、Levenberg-Marquardt-Fletcher法(莱文贝格-马夸特-弗莱彻算法,简称LMF算法)[7]、QNew算法(拟牛顿算法)、FM算法(快速拟合算法)等,以及粒子群算法、遗传算法[8-9]等智能算法。运用这些算法时会遇到很多实际问题,如目标函数具发散性,或有些算法拟合过程中耗时过长而无法满足软件编制的要求。为了避免此类问题,研究人员进行了多种尝试。本次研究将尝试在试井曲线拟合中引入一种自动拟合算法 —— 信赖域算法。
1 信赖域算法理论
信赖域算法是一种求解非线性优化问题的数值方法,也是一种迭代算法,即从给定的初始解出发,通过逐步迭代,不断改进,直到获得满意的近似最优解为止[10]。
首先,在每次迭代中,给出一个信赖域,这个信赖域一般是当前迭代点xk的一个小邻域;然后,在这个邻域内求解一个子问题,得到试探步长Sk;接着,通过某个评价函数来判断是否接受该试探步,并确定下一次迭代的信赖域。如果试探步长被接受,则有,xk+1=xk+Sk;否则,xk+1=xk。
新的信赖域大小取决于试探步长的优劣。如果试探步长较优,就在下一步使信赖域扩大或保持不变;否则,应缩小信赖域。定义当前迭代点xk的邻域定义为:
(1)
式中:Ωk为当前迭代点xk的邻域;Rn为对称正定矩阵;Δk为第k步的信赖域半径。
目标函数在极值点附近,近似于1个二次函数。对于无约束优化问题,利用二次逼近,构造式(2)所示信赖域子问题:
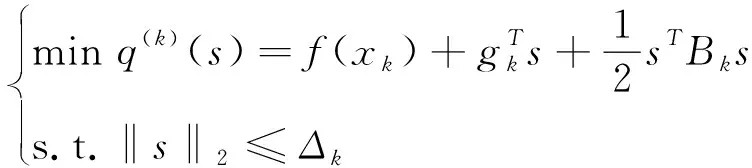
(2)
式中:s=x-xk;gk是目标函数f(x)在当前迭代点xk处的梯度;Bk∈Rn×n对称,是f(x)在xk处Hesse阵2f(xk)或者其近似值;q(k)(s)是目标函数f(x)的二次逼近式,即二次模型函数。
假设Sk是式(2)的解,则目标函数f(x)在第k步的实际下降量(真实下降量)Aredk为:
Aredk=f(xk)-f(xk+Sk)
(3)
二次模型函数q(k)(s)的下降量(预测下降量)Predk为:
Predk=q(k)(0)-q(k)(Sk)
(4)
定义比值rk:
(5)
rk衡量了二次模型与目标函数的逼近程度,其值越趋近于1,表示接近程度越好。因此,我们也可以用rk来确定下次迭代的信赖域半径。
2 信赖域算法实现步骤
信赖域算法的实现可分以下6个步骤。
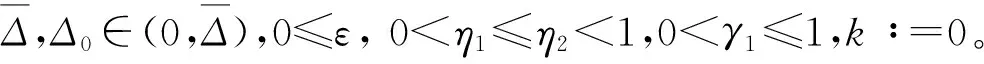
Step2如果‖gk‖≤ε,则停止。
Step3近似求解子问题,即式(2),得到Sk。
Step4计算f(xk+Sk)和rk,令
Step5校正信赖域半径,令
Δk+1∈(0,γ1Δk],ifrk<η1
Δk+1∈[γ1Δk,Δk],ifrk∈[η1,η2)
Step6产生Bk+1,校正q(k),令k∶=k+1,转Step 2。
3 算法代码及效果分析
3.1 部分关键代码
根据信赖域方法原理及实现步骤,编制相应的试井曲线自动拟合模块,部分关键代码如下:
public static List
{
∥从CSK1_parameter1_duration1_rate2中分别提取拟合参数CSK、常规参数、产量持续时间、关井前各个产量、拟压力历史数据恢复数据
Array
…∥此处符号代表省略部分代码
…
∥从data1中提取时间数据和压差数据
Array
Array
∥从data2中提取拟压力变换表述
Array
Array
…∥此处符号代表省略部分代码
…
watch.Start();∥开始监视代码运行时间
∥调用matlab部分
MLApp.MLApp matlab = ToolFunc.creatematlab();
∥把对应数据传输到matlab运算平台
matlab.PutWorkspaceData(“x1”, “base”, x0);
matlab.PutWorkspaceData(“y1”, “base”, y0);
matlab.PutWorkspaceData(“pressure1”, “base”, pressure0);
matlab.PutWorkspaceData(“pseudopressure1”, “base”, pseudopressure0);
matlab.PutWorkspaceData(“para”, “base”, CSK1_parameter1_duration1_rate1_tmp);
matlab.PutWorkspaceData(“CSKR”, “base”, CSKR1);
matlab.PutWorkspaceData(“duration0”, “base”, duration0);
matlab.PutWorkspaceData(“rate0”, “base”, rate0);
matlab.PutWorkspaceData(“boud0”, “base”, boud1);
matlab.PutWorkspaceData(“rate_times0”, “base”, rate_times0);
watch.Stop();∥停止监视
TimeSpan timespan = watch.Elapsed;∥获取当前实例测量得出的总时间
System.Diagnostics.Debug.WriteLine(“执行时间:{0}(s )”,timespan.TotalMilliseconds);
∥执行matlab的拟合函数
watch.Restart();
∥针对不同试井模型,调用对应的模型方法matlab.Execute(@“[bestCSK,resnorm]=Closed_Finite_Circle(x1,y1,pressure1,pseudopressure1,CSKR,para,duration0,rate0,rate_times0,boud0)”);
watch.Stop();∥停止监视
timespan =watch.Elapsed;∥获取当前实例测量得出的总时间
System.Diagnostics.Debug.WriteLine(“函数拟合时间:{0}(毫秒)”, timespan.TotalMilliseconds);
BestCSK = matlab.GetVariable(“bestCSK”, “base”);
…∥此处符号代表省略部分代码
…
}
3.2 效果分析
应用均质无限大、圆形封闭边界理论模型对信赖域算法进行效果分析,并与解决非线性最小二乘法问题常用的LM算法进行对比。
(1) 均质无限大油藏模型分析。某均质无限大油藏,原始地层压力为30 MPa,其中某油井在无污染条件下以100 m3d的生产水平稳定生产6 h。其他基本参数有:储层有效厚度,10 m;体积系数,1.0;孔隙度,0.2;黏度,0.5 mPa·s;综合压缩系数,4×10-4MPa-1;井半径,0.1 m。油井压力与时间数据如表1所示。
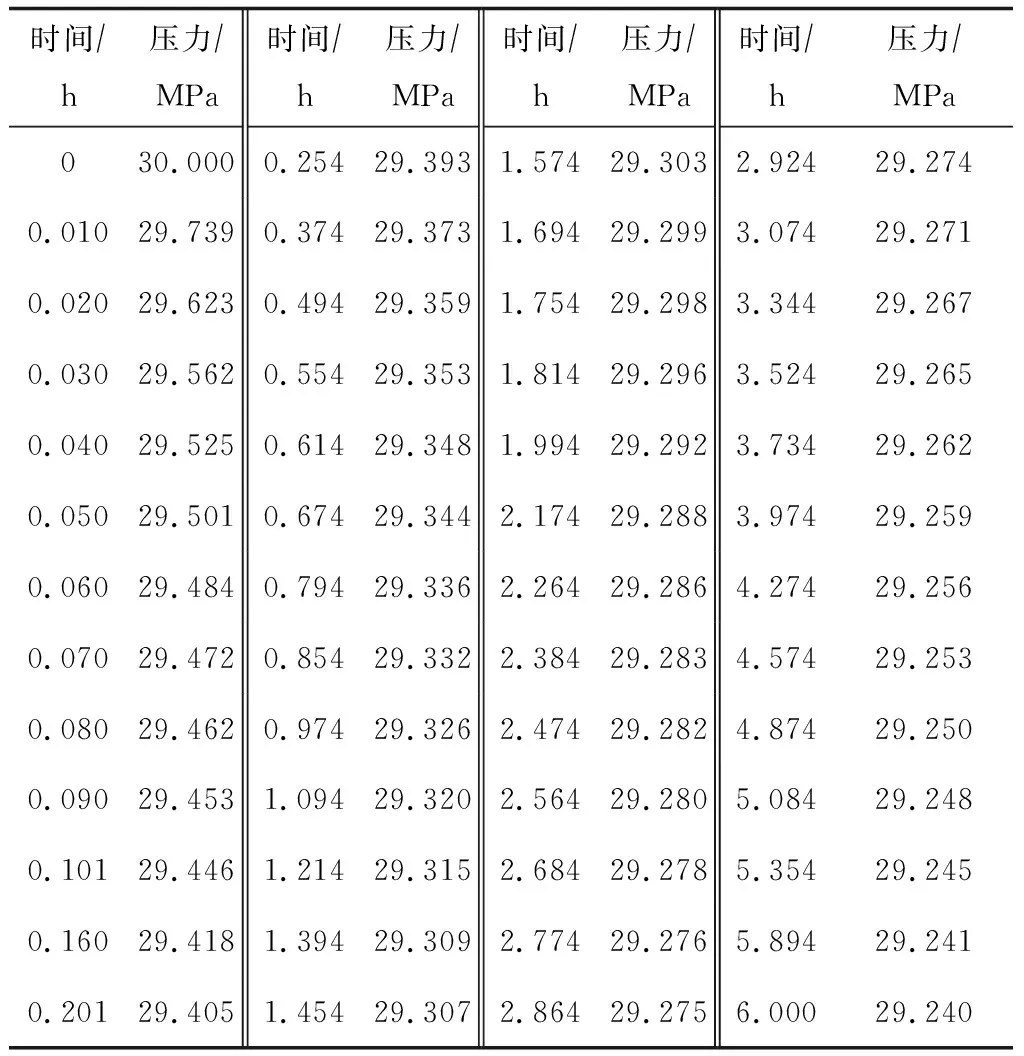
表1 某油井压力、时间数据
针对待拟合参数井筒储集系数(C)、 表皮系数(S)、渗透率(K),分别采用LM法和信赖域法,以压力误差平方和最小为目标函数,对压力降落双对数曲线进行自动拟合。这2种方法获得的最佳拟合参数差异非常小(见图1、图2),其数值均在C=0.100 1 m3MPa,S=0.001,K=98.7×10-3μm2附近。

图1 LM算法自动拟合效果图
(2) 均质圆形封闭边界模型分析。某封闭有限圆气藏原始地层压力为34.473 8 MPa,其中某气井以200×104m3d的生产水平稳定生产。其他基本参数有:储层有效厚度,30 m;体积系数,0.003 817 4,孔隙度,0.2;黏度,0.026 528 mPa·s;综合压缩系数,0.019 192 MPa-1;井半径,0.091 44 m;地层温度,373.15 K。
针对需拟合参数井筒储集系数(C)、表皮系数(S)、渗透率(K)、封闭有限圆半径(R),采用LM法和信赖域法进行自动拟合。这2种方法拟合所得的结果基本一致(见图3、图4),其数值均在C=1.1 m3MPa,S=3,K=486.1×10-3μm2,R=1 512.7 m 附近。
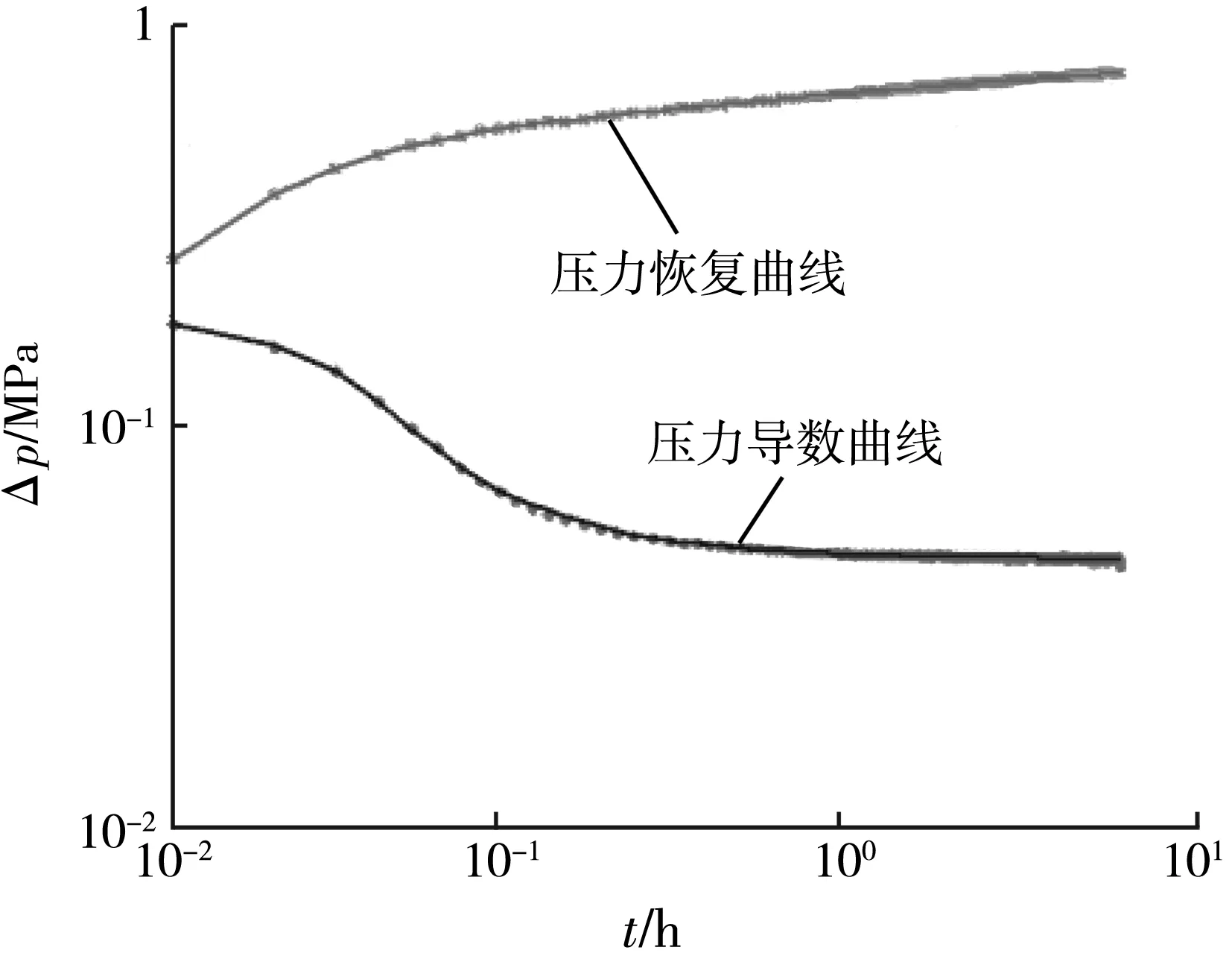
图2 信赖域算法自动拟合效果图
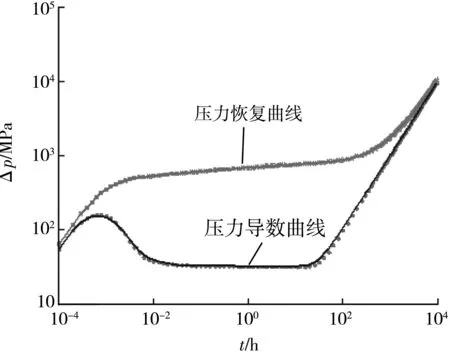
图3 LM算法自动拟合效果图

图4 信赖域算法自动拟合效果图
对比2个模型的计算结果(见表2)。这个模型的拟合误差,即拟合计算压力值与实测压力值的相对误差,为10-3。在此拟合精度下的试井解释结果,可满足生产解释的要求,解释结果与商业软件解释结果基本一致。但在运行效率方面,LM算法耗时较长,信赖域算法的效率明显较高。

表2 两种模型的算法结果对比
4 结 语
本次研究中,在试井曲线拟合时采用了信赖域算法。运用信赖域算法,可对试井曲线进行自动拟合算法,实现对地层未知参数的最优化求解。通过实例验证,认为信赖域算法能够在较快时间内完成自动拟合,且拟合误差低于0.005%,能满足试井解释分析中参数求解的要求。
