基于椭圆滤波和RAT/FRT 的雷达信号调制样式识别
2019-09-17万铮,王建,张宁
万 铮,王 建,张 宁
(中国船舶重工集团公司第七二四研究所,南京 211106)
0 引言
雷达波形的脉内调制类型及调制参数能够提供丰富的辐射源工作模式及战术意图信息。正因此,对雷达信号脉内调制特性的自动分类识别方法,近年来一直是电子战领域的研究热点。文献[1-3]分别采用崔- 威廉斯分布(CWD)、维格纳-威利时频分布(WVD)和正交镜滤波器组(QMFB)等时频分析手段来研究LPI 雷达信号调制类型的分类识别方法。文献[4-5]中分别使用了拉东-维格纳变换(RWT)和拉东正交滤波镜组技术来对低截获概率(LPI)雷达信号进行调制分类。但是上述的分类识别技术都需要较强的先验知识,并且都是计算密集型,难以适应现代电子情报侦察系统对辐射源快速分类识别的要求。文献[6]提出了一种基于维格纳分布的LPI 雷达信号调制特性自动分类方法,但处理流程中引入的信号交叉项,将会对波形可读性和调制分类准确率造成一定影响。鉴于此,本文提出一种改进的雷达信号脉内调制特性自动分类识别方法。该方法首先采用模糊域椭圆高斯滤波算法对雷达脉冲信号进行预处理,以有效抑制交叉项,改善信噪比,然后基于平滑伪维格纳分布(SPWVD)获取瞬时频率,再应用RAT、FRT 等技术手段提取波形调制特征,进而实现对雷达信号调制类型的自动分类。本文所提方法可显著提升低信噪比条件下对雷达信号调制特征的分类识别准确率。
1 概述
1.1 雷达信号调制类型
在当前复杂密集的电磁环境中,各类雷达系统广泛使用宽带信号调制波形来提高雷达系统分辨力,并减少信号被截获概率。常用的3 种获得宽频谱的方法,分别是周期地改变信号频率、利用高速数字信号调制和直接展宽信号频谱。各类常见的雷达信号的调制方式主要包括LFM、BFSK、HOB、Frank、P1 码、P2 码、P3 码、P4 码等。本文针对上述各种雷达信号脉内调制类型,研究可实现自动分类识别的方法。
1.2 时频分析处理方法
通过时频分析处理方法,可将一维时域信号映射至二维时频平面,以直观地展现信号在不同时间/频率区间的能量密度。因此,时频分析及时频域联合滤波技术被广泛应用于雷达脉冲串等时变信号的分析及处理[7]。WVD 是一种经典的科恩类双线性时频分析方法[8]。与FFT 和傅里叶变换之间的关系类似,伪维格纳分布(PWVD)是WVD 的有限离散算法,如式(1)所示,由x(t)的采样在WVD 后加窗x[l]得到:
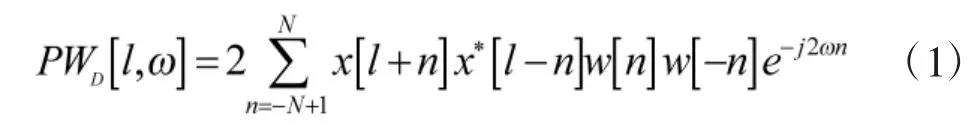
其中,w[n]是长度为2N 的实值窗。上述定义中窗函数的作用是使WVD 局部化,从而可在一定程度上压缩信号的交叉项。此外,SPWVD 通过将PWVD 与平滑函数做卷积处理,可进一步凸显波形在时频域的聚集性[9-10]。本文主要采用SPWVD 对待分类识别的雷达信号波形进行预处理。
2 待分类雷达信号预处理方法
2.1 加性高斯白噪声抑制技术
为了抑制截获信号中的加性高斯白噪声(AWGN),可以在WVD 变换域取零频域实现。对于一个信号z(t),在WVD 变换中的零频域实际上是它自身的对称相关函数。记作:
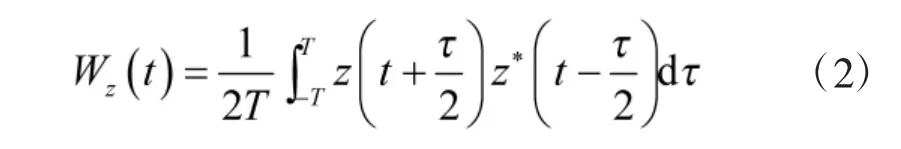
其中,T 为脉冲周期。当T 的值达到一个较大值时,这个对称相关函数就可以有效减小加性噪声,且无需先验知识。这就是基于WVD 的去噪技术[11]。
2.2 信号的模糊域椭圆高斯滤波
在上节所述的WVD 变换中,信号的交叉项会对后续调制分类的准确度造成影响。椭圆滤波核可以过滤交叉项的频谱和大部分加性噪声,并保留各独立分量的主频谱。因此,对侦收信号进行模糊域椭圆高斯滤波处理获得SPWVD,可以抑制交叉项对脉内调制方式分类识别的影响,增强信号的波形表示。
首先通过加窗得到PWVD 的时频面PWD[l,w],将此时频面与一个椭圆滤波核hell[l,w]卷积后的结果可以写作:
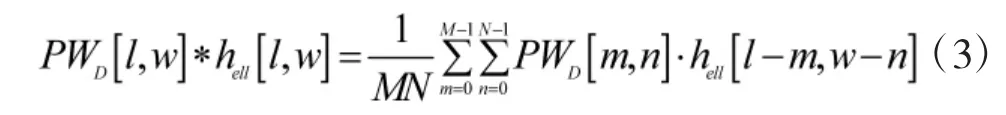
利用模糊函数表示PWVD 的频谱,根据傅里叶卷积理论,上式可变为:
问卷《在校大学生校园需求调查表》内容涉及大学生经济水平、消费偏好、消费动机、需求方向以及需求个性化程度5项内容。

其中,Hell[n,v]是滤波器的传递函数。一个理想的二维椭圆频率响应滤波器可写作:

由此,再利用逆傅里叶变换可得SPWVD。
为了进一步消除因滤波引起的频谱模糊和抖动,可以利用高斯函数优化上述滤波过程[12]。所采用的椭圆高斯滤波器的传递函数是:
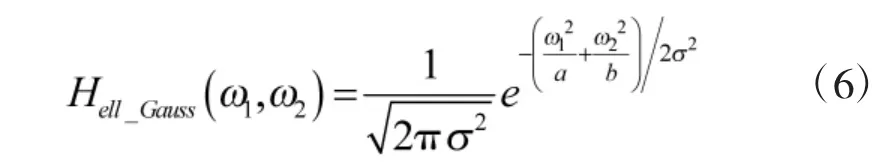
其中,σ 是二维圆形高斯光斑在两个维度上的扩展值,a 和b 分别是椭圆的长短半轴。
对于最常见的LFM 信号,需要将椭圆滤波核旋转一个角度以匹配调频斜率。设旋转的角度是θ,则有:
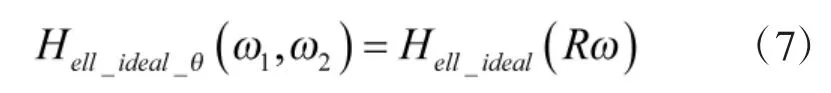
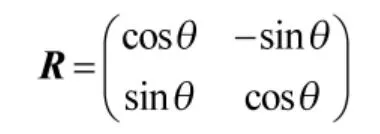
所以在旋转θ 角后,得到的旋转椭圆高斯滤波核为:

将模糊域上的椭圆高斯滤波核与模糊函数矩阵逐元素相乘,对结果进行二维逆傅里叶变换,即可得到最终的SPWVD[13]。图1 表示了完整的模糊域椭圆高斯滤波处理流程。
从所得SPWVD 中提取出零频信息等特征,可用于进行信号调制方式的分类识别。
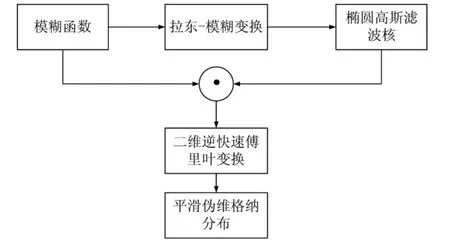
图1 模糊域椭圆滤波框图
3 基于RAT/FRT 的特征提取和脉内调制类型分类
RAT 和FRT 分别是针对LFM 信号和P2 码信号的特征提取和调制方式分类识别算法。通过上节所述的交叉项抑制和降噪预处理后,再采用RAT 和FRT 算法对截获信号进行特征提取,可实现对信号脉内调制方式的分类识别。
对于一个LFM 信号,它的模糊函数只有一个主脊线通过原点,其他调制类型则多于一个。利用RAT 算法可以将模糊函数中的脊线变换到极坐标中:


对于BFSK 和HOB 信号,直接利用快速傅里叶变换测量信号的3 dB 峰值,当归一化频谱出现2 个或以上的峰值时,信号是BFSK 信号。再利用瞬时频率的中值滤波的标准差区分出HOB[14]。
文献[4]介绍了利用RWT 识别P2 码的方法。RWT 的公式可以写作:
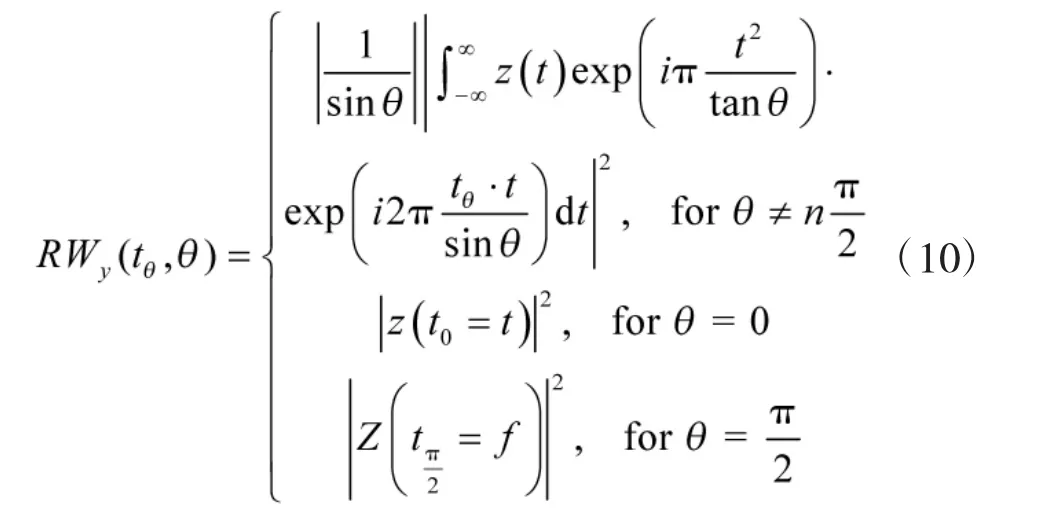
这是一种需要人工观察才能达成的分类方法。而另一种重要的时频分析工具FRT 的公式为:
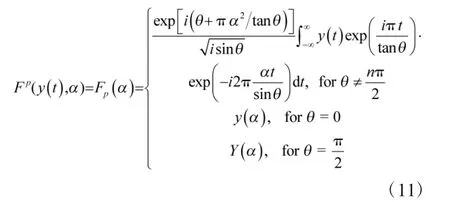
对比两式可以得到RWT 与FRT 的关系:
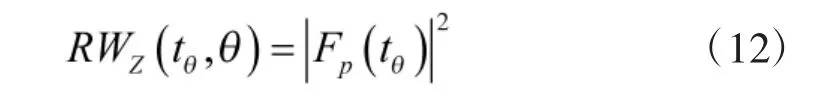
因此,可以利用FRT 代替RWT 实现对P2 码的自动分类识别。找到FRT 中对应最大幅值的角度:

当θm大于90°时,信号是P2 码,由此可将P2码调制信号识别出来。
Frank 和P3 的最大码元相位出现在码串中心,所以信号在FRT 计算中最大频谱变化区域也出现在信号中心。P1 和P4 码的最大频谱变化则发生在信号尾部[15]。对信号维纳瞬时频率进行中值滤波,可提取有效尖峰数f(由于Frank 和P3 码在首尾码元的不准确性,所以移除首尾10%的数据)。对f 作微分得到f',归一化后可得到直方图[16]。对于Frank和P1 码,它们的直方图有两个以上的直条,而P3、P4 码则反之。根据以上两个性质可以将剩余的4 种调制方式一一分辨出来。
通过以上步骤可以依次区分出LFM、BFSK、HOB、P2、Frank、P3、P1 和P4 码调制类型的信号。图2 给出了上述信号调制方式分类识别算法的处理流程。

图2 LPI 波形调制分类算法流程图
4 算法仿真及性能分析
本节对上一节所提出的脉内调制方式分类识别算法的有效性进行仿真分析。首先分析预处理算法的降噪性能。对于脉宽为50 μs 的LFM 信号,在3 dB 的加性高斯白噪声环境下,未经过预处理直接进行滤波和先经过预处理再进行滤波后的输出信号分别如图3 和图4 所示,比较两图中的波形可见,相比于未经预处理直接滤波的信号,通过预处理过程可以有效提升后续滤波处理输出信号的信噪比。
针对上节中提出的基于FRT 的P2 码分类算法,采用脉宽10 μs 的P1 和P2 码信号,在-10 dB的噪声环境中进行仿真分析,通过FRT 变换,图5和图7 显示了与时间对应的各分数阶FRT 输出,图6 和图8 显示了FRT 处理后各角度峰值输出,通过对比图中最大幅值对应的角度可以区分出P2 码。
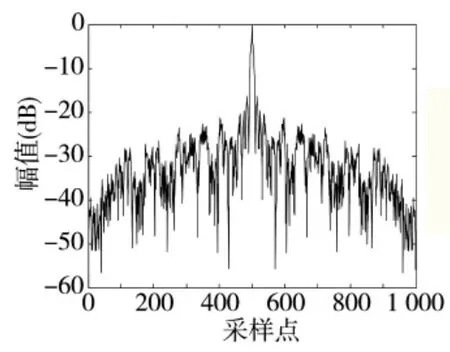
图3 直接进行匹配滤波的输出信号
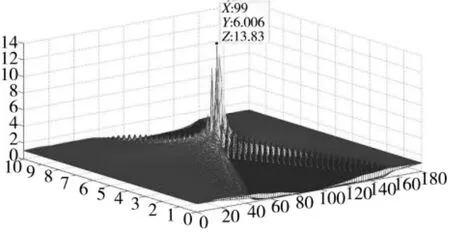
图5 P2 码在各时刻各分数阶FRT 输出
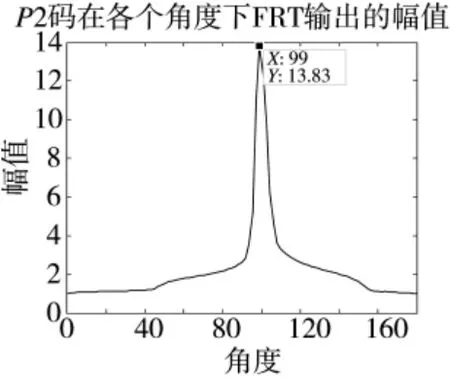
图6 P2 码经过FRT 处理后各角度峰值输出
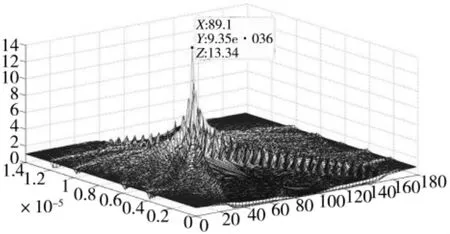
图7 P1 码在各时刻各分数阶FRT 输出
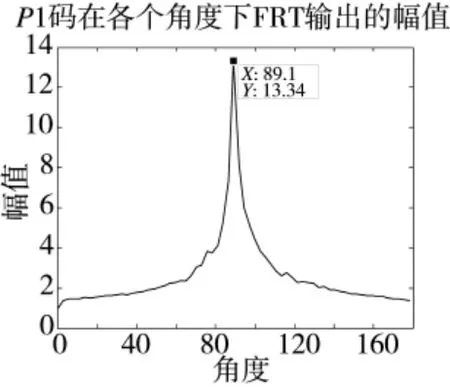
图8 P1 码经过FRT 处理后各角度峰值输出
为了验证上述调制分类算法对不同信号波形的普适性,采用10 μs、50 μs 和100 μs 3 种脉宽,采样率为100 MHz 的信号进行重复仿真验证。仿真时假定信噪比以1 dB 步进,从-15 dB 变化到10 dB。下页表1 显示了在-10 dB 信噪比下,上述调制分类算法的分类准确度。在相同准确度(95%)条件下,本文提出的调制分类算法和文献[16-17]给出的调制分类算法所需的最低信噪比见表2。可以看出,在同等调制分类准确度条件下,本文提出的算法可以适用于更低的信噪比。
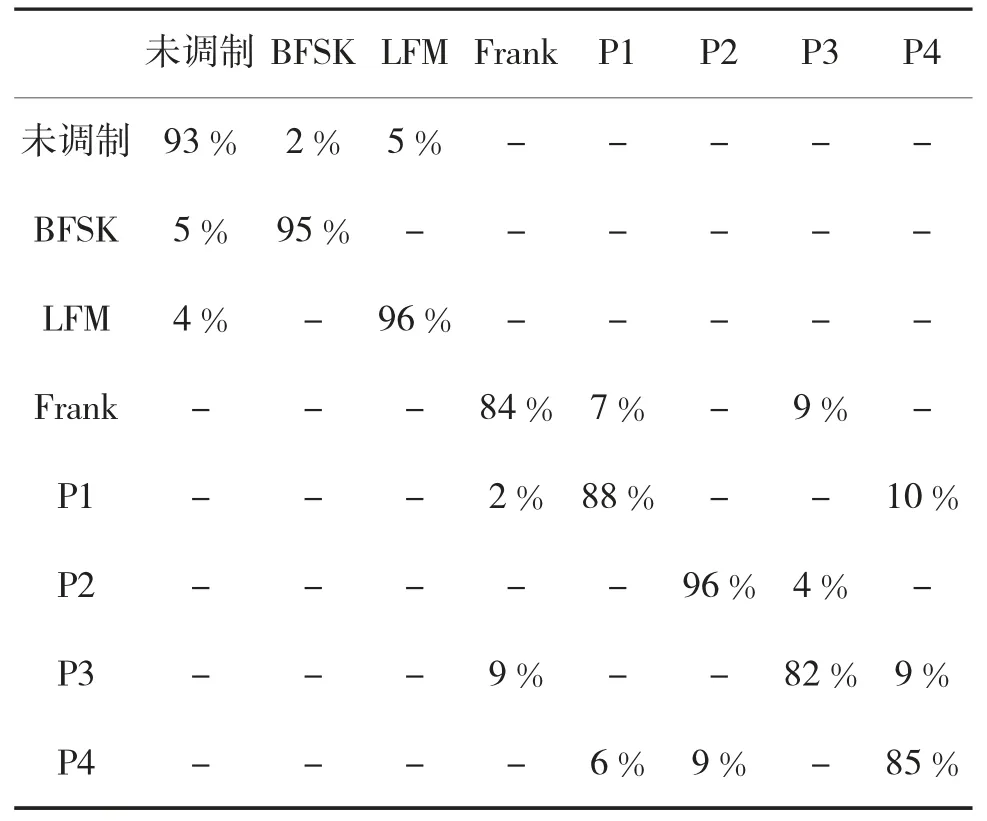
表1 各调制类型分类准确度(-10 dB 信噪比)

表2 算法所需信噪比阈值仿真结果
5 结论
本文讨论的雷达信号脉内调制方式自动分类识别算法,利用模糊域椭圆高斯滤波等手段进行信号预处理,再采用RAT、FRT 等技术提取信号脉内特征并进行自动调制分类。在不同信噪比条件下,对不同脉宽的调制信号进行了大量调制分类识别性能仿真。结果表明,本文提出的调制分类识别算法,可以在较低信噪比条件下,对多种调制类型的信号进行准确度达95%的调制分类。对LFM、P2 码等信号,可以在-10 dB 信噪比条件下进行高准确度的调制分类,且算法结构简单,处理运算量小,易于工程应用。
