基于证据理论的直觉模糊群决策方法

常 政，项华春，陈云翔，罗承昆

（空军工程大学装备管理与无人机工程学院，西安 710051）

0 引言

近年来，多属性群决策问题受到了越来越多的关注，在解决决策择优［1-3］、威胁评估［4］、效能评估［5］等诸多问题有着广泛的应用。在管理决策过程中，由于客观事物的复杂性和不确定性，决策者通常难以用精确的实数值来表达偏好信息，直觉模糊数的提出和发展为解决此类问题提供了新思路。

目前已有很多文献都展开了研究，采用的方法也较多，研究的关键问题主要体现在属性权重的确定、专家权重的确定以及决策信息的集结。

1）属性权重的确定

决策属性权重的确定，通常结合熵理论对直觉模糊数进行处理。文献［2］综合考虑直觉性和模糊性对不确定信息的影响，提出了一种新的直觉模糊熵，并基于熵最小化的原理建立非线性规划模型确定属性权重；文献［6］对直觉模糊熵进行了分类比较，按照直觉模糊熵的度量含义不同，分别从犹豫度、几何距离、概率和不确定性框架4 个方面进行了归纳总结，并提出一种客观权重的确定方法；文献［7］根据直觉模糊熵的定义，在计算属性权重时，考虑了犹豫度对权重的影响，对计算公式进行了改进，提出了新的度量方法，并证明了其合理性。

2）专家权重的确定

文献［8］在对直觉模糊多属性群决策中，提出了相似度的概念，把群决策转化为单人决策；文献［1］通过将各专家给出的直觉模糊集决策矩阵转化为决策向量，提出基于直觉模糊决策向量的欧几里得相似度的专家权重确定方法；文献［9］通过单一专家的个人决策矩阵和其他所有决策者的决策矩阵之间的距离来确定决策者权重。结合以上研究确定专家权重的优势，应用TOPSIS 法和Jousselme 距离，融合相似度与接近度来确定专家权重，使结果更加科学合理。

3）决策信息的集结

确定专家权重和属性权重后，运用不同的集结方法便可得到各方案评价结果。文献［1，10-11］通过TOPSIS 法来对专家群的决策信息进行综合集成，根据个人评价信息与群体之间的距离信息进行评价，可能会过分削弱一些偏差度较大评价信息的影响权重，失去部分决策者信息；文献［12］在提出了一系列的信息集成算子，并将其应用于多属性群决策问题中，但是在运用这些算子处理决策问题之前，需要获取属性权重和自然状态发生概率的相关信息，若用于处理属性权重完全未知的情况，不一定可靠。因此，本文应用改进的证据理论进行信息集结，一方面Dempster 组合规则具有良好的信息聚焦性能，降低结果的不确定性；另一方面，可以运用证据权进行证据信息的修正，避免信息的不可靠造成证据之间重要程度的差异。

基于此，本文提出一种新的基于证据理论的直觉模糊群决策方法。将解决问题的关键分为属性集信息集结和专家集信息集结两部分，在计算属性权重和专家权重后，运用证据权理论，分别对属性集和专家集的Mass 函数进行修正，再通过Dempster 组合规则进行合成，最终得出方案集的Mass 函数向量进行方案排序，并结合算例验证了方法的有效性。

1 预备知识

1.1 直觉模糊集

定义1［13］设X 是一个论域，则论域X 上的一个直觉模糊集定义为：

1.2 直觉模糊熵

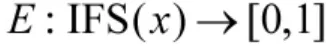
1.3 证据理论

定义4［15］设Bel1，Bel2，…，Beln是同一识别框架Θ 的信任函数，m1，m2，…，mn为对应的Mass 函数，有

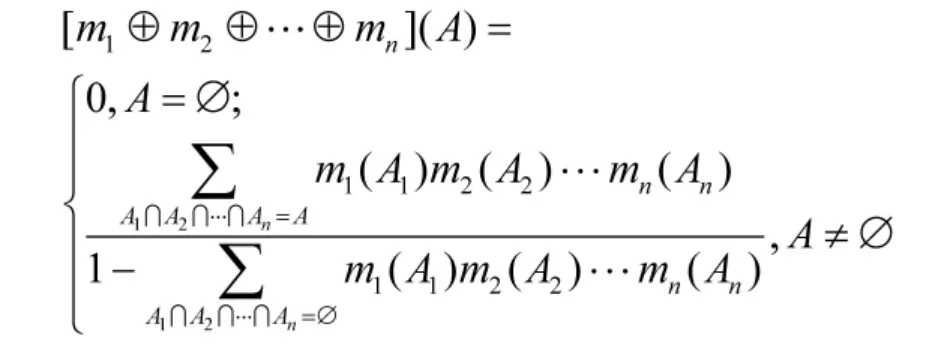
2 基于证据理论的直觉模糊群决策模型

2.1 问题描述与评价信息处理

对于属性权重和专家权重完全未知的多属性群决策问题，由K 名专家Pk（k=1，2，…，K）组成的专家集，针对由n 个备选方案的m 个属性oi（i=1，2，…，m）组成的属性集O，由n 个备选方案xj（j=1，2，…，n）构成方案集X 展开评价。

运用D-S 证据理论进行信息集结，首先需要构建各证据下不同方案的Mass 函数，主要利用记分函数和属性的不确定度来构建。

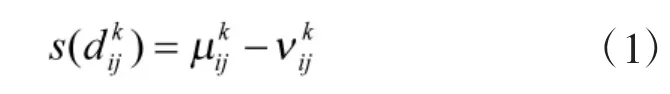
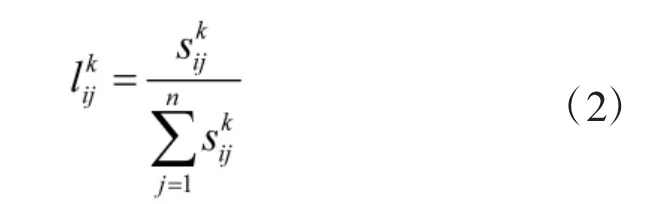
运用证据理论进行决策，在求解各证据下不同方案的Mass 函数时，要合理地确定属性不确定度，本文运用灰色关联法，根据各属性信息之间的相似或相异程度来衡量该属性与其他属性的匹配程度，某个属性相对于其他属性而言，越匹配属性体系的平均信息，则该属性包含的信息对决策越有利，即该属性不确定度越低，反之亦然。属性oik的q 阶不确定度可定义为

其中，q 不确定度阶数，为提高分辨率，采用欧式距离，取q=2，

则专家Pk对属性oi关于方案集的Mass 函数可表示为

因此，专家Pk对属性集关于方案集的Mass 函数矩阵为

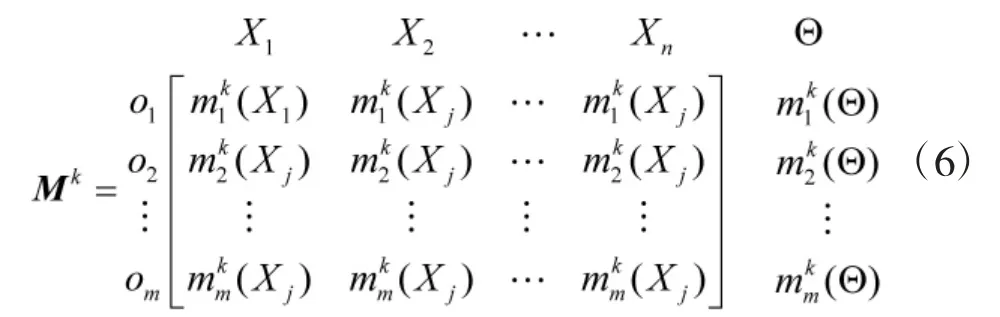
2.2 属性集信息集结

2.2.1 考虑直觉模糊熵的属性权重计算

Atanassovd［6］等于1986 年提出直觉模糊集的概念后，直觉模糊熵也随之发展起来，在处理模糊信息和不确定信息方面也更加灵活。文献［7］根据直觉模糊熵的定义，在计算属性权重时，考虑了犹豫度对权重的影响，对计算公式进行了改进，提出了新的度量方法，避免了隶属度与非隶属度相同的情况下计算失效的问题，并证明了其合理性。因此，本文采用文献［7］中所构建的改进的直觉模糊熵计算公式：

结合本文的问题描述，即可由式（7）得到第i 个属性的直觉模糊熵为

第k 个专家的第i 个属性的权重为

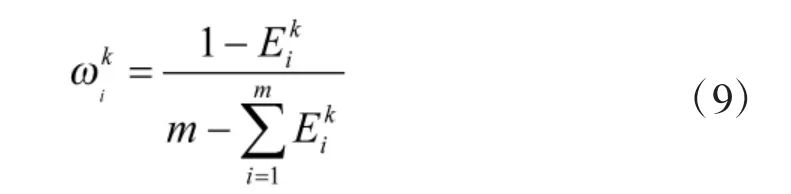
2.2.2 属性集证据信息修正与合成

构建Mass 函数后，为了避免信息的不可靠造成证据之间重要程度的差异，保证每条证据信息处于同样重要的位置，需要进行修正。

综合考虑属性之间的差异，针对属性权重，采用证据权将专家Pk对属性集关于方案集的Mass 函数进行修正。

根据通过Dempster 组合规则，将修正后的专家针对属性集关于方案集的Mass 函数进行合成。得到专家Pk关于方案集的Mass 函数向量为Mk。

2.3 专家集信息集结

2.3.1 考虑相似度和接近度的专家权重计算

在群决策过程中，由于专家之间知识、理解和背景等的不同，所提供的决策信息往往会有所差异，因此，有必要对各专家的重要性进行区别。专家的权重可以由专家集关于方案集的Mass 函数分析得出，主要考虑两个方面，一方面是相似度，用于表示决策者Pk的个人决策矩阵和所有决策者构成的综合群决策矩阵之间的相似程度；另一方面是接近度，用于表示决策者Pk的个人决策矩阵和除了决策者Pk的其他所有决策者构成的综合群决策矩阵之间的接近程度。据此分析，在求解决策者权重时，主要包括3 个步骤：一是运用TOPSIS 法确定相似度，二是运用Jousselme 距离确定接近度，三是综合确定专家权重。

1）运用TOPSIS 法确定接近度

采用TOPSIS 法来确定决策者权重，首先需要确定正负理想解：

设正理想解为

负理想解为

计算各方案到正负理想解的距离

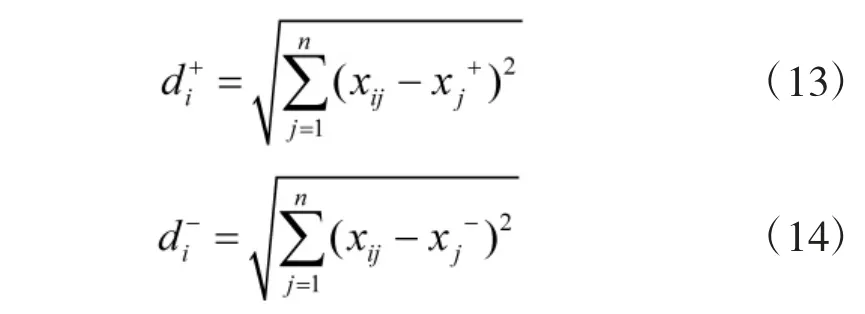
计算各方案与总体方案理想解的接近程度

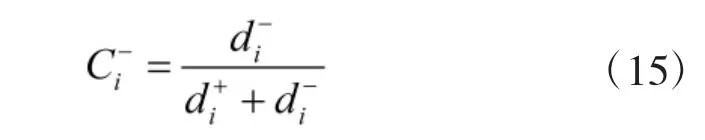
即可得出专家权重为

2）运用Jousselme 距离确定接近度

运用Jousselme 距离确定接近度，即运用两两证据间的Jousselme 距离计算证据相似性，进一步得出该证据被其他证据支持的程度，归一化即得出专家权重。具体实现步骤如下。

定义5［16-17］设识别框架Θ 上有两个Mass 函数m1和m2，两者之间的距离可以表示为

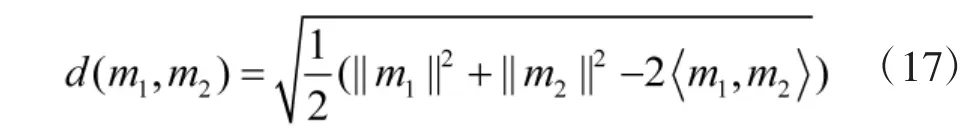
对得到的证据计算距离，并表示成证据距离矩阵：

证据体之间的证据mi和mj之间的相似性测度表示为

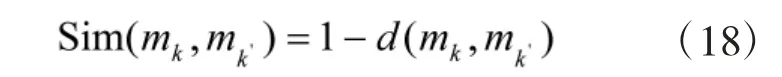
用Sup（mk）来表示mk被其他证据支持的程度。若两个证据的相似程度越高，其相互支持的程度越大，Sup（mg）的值也就越大；反之亦成立。其计算公式为

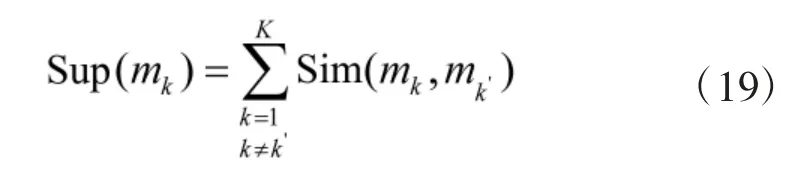
即可得到专家权重为

3）综合确定专家权重

为了综合地考虑相似度和接近度，通过折衷系数η（0≤η≤1）加以综合，最终构造了决策者Pk关于方案集的组合权重

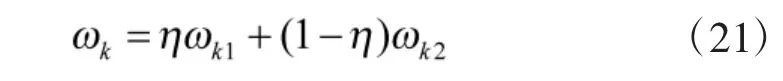
式（21）可以通过控制折衷系数η 的改变在相似度和接近度之间进行权衡。若更关注相似度，则取0.5＜η≤1，若更关注接近度，则取0≤η＜0.5，若无偏好则取η=0.5。为平衡相似度和接近度，取η=0.5。

2.3.2 专家集证据信息修正与合成

同理2.2.3，考虑专家之间的差异，针对专家权重，采用证据权将专家Pk关于方案集的Mass 函数进行修正

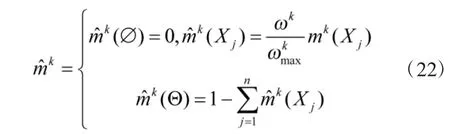
根据证据组合规则，将修正后的专家集关于方案集的Mass 函数进行合成，即可得到最终关于方案集评价向量

基于上述分析，基于证据理论的直觉模糊群决策流程如下：

步骤1：获取专家意见得出判断矩阵；

步骤2：属性集Mass 函数的构建；

步骤3：属性权重的确定；

步骤4：属性集证据信息集结；

步骤5：专家权重确定；

步骤6：专家集证据信息集结；

步骤7：对方案进行排序。

3 算例分析

为了分析某型飞机大修能力水平，需要对3 个厂家的大修效能进行评估。经研究决定，邀请空军维修保障领域的专家P1，P2，P33 人组成的专家集，对某3 家大修企业x1，x2，x3的大修效能进行评估，主要从任务完成率o1、人员技术水平o2、备件满足率o3、设备完好率o4、信息化建设水平o55 个方面进行分析。具体的计算过程如下：

步骤1：专家P1，P2，P3给出的每家大修企业关于属性集的直觉模糊评价值分别为

步骤2：运用式（1）、式（2）得到专家P1的记分函数矩阵为

运用式（3）、式（4）计算属性不确信度为：

运用式（5）即可确定专家P1对属性集关于方案集的Mass 函数矩阵为

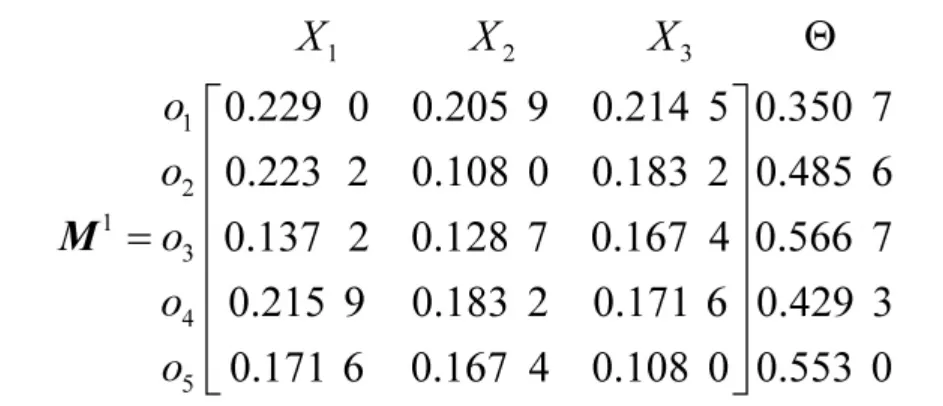
步骤3：运用式（8）、式（9）计算专家P1的属性权重向量为

步骤4：考虑属性权重，运用式（10）对Mk进行修正，进而通过Dempster 组合规则进行合成。得到专家P1关于方案集的Mass 函数向量为

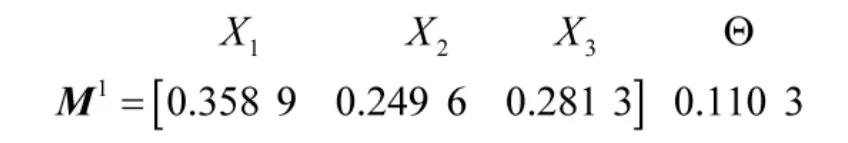
同步骤2～步骤4 分别得到专家P2，P3关于方案集的Mass 函数向量，组合得到专家集关于方案集的Mass 函数矩阵M

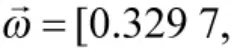
步骤6：运用式（22）对专家权重进行修正，进而通过Dempster 组合规则进行合成。得到专家P1，P2，P3关于方案集的Mass 函数向量为

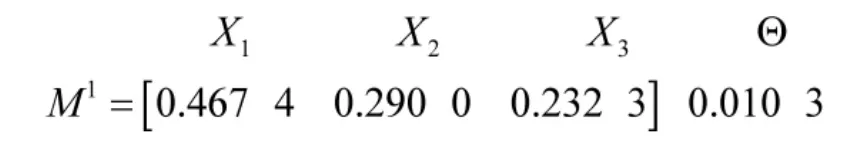
步骤7：得出3 个方案的排序为

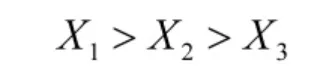
即第1 个大修厂的效能较好，验证了方法的可行性和有效性。主要有以下优势：一是通过计算相似度和接近度来确定专家权重，更加全面合理；二是通过属性权重和专家权重对决策证据信息进行修正，有利于避免证据之间的潜在冲突，结果也更加客观；三是通过Mass 函数向量对方案进行优劣排序，可明显对比各方案的评价指标，有利于作出判断。

4 结论

针对专家权重和属性权重完全未知的直觉模糊群决策问题，首先，基于记分函数和属性的不确信度构建Mass 函数，运用改进的直觉模糊熵计算公式确定属性权重，并引入证据权进行修正，运用Dempster 组合规则展开属性集信息集结；其次，基于TOSPSIS 法确定相似度，基于Jousselme 距离计算接近度，考虑相似度和接近度进行专家权重计算，引入证据权进行修正，运用Dempster 组合规则对专家集关于方案集的Mass 函数进行集结，得出专家集针对方案集对于属性集的Mass 函数向量，即可进行方案优劣的判断，最后通过算例计算验证了方法的可行性和有效性。